一種高速重載碼垛機器人誤差分析

吳 振，萬英和，吳連松，饒金海，武冰昕

（1.北京機械工業自動化研究所有限公司，北京 100120；2.北京萬集科技股份有限公司，北京 100193）

0 引言

國產碼垛機器人經過多年發展雖然取得了顯著的成果，但是在末端定位精度上與國外碼垛機器人相比還是有一定的差距，提高機器人末端定位精度主要途徑是進行誤差補償，而誤差補償的理論基礎是建立機器人末端位姿誤差模型[1～3]。國內外許多學者在該領域做了大量的研究工作，并取得了許多成果[4～6]。童上高[4]等人，基于攝動法對沃迪公司的TPR-120/200碼垛機器人進行了定位誤差分析，并提出了各個可能引起末端位置誤差的因素以及相應的誤差補償算法。寧鳳艷[5]等人同樣基于攝動法對MJR混聯碼垛機器人進行了誤差分析，建立了其位姿誤差模型，通過數值仿真分析了結構偏差，這種分析思路可以作為常用機器人誤差分析方法。

本文基于D-H參數法建立碼垛機器人構件間誤差傳遞函數和手腕體末端位姿誤差模型。綜合考慮各個可能引起末端位姿誤差的因素，從中提取對定位誤差影響較顯著的因素，研究其對位姿誤差的具體影響，為碼垛機器人加工、裝配過程提供理論依據。分析機器人結構參數誤差一定時，機器人末端位置誤差隨驅動關節轉角的變化規律，之后研究了在重力作用下驅動關節柔性與桿件柔性對于末端誤差的影響，并對不同位姿下的末端誤差進行了計算。

1 建立碼垛機器人誤差模型

1.1 D-H參數法建模

基于D-H參數法[7]，建立碼垛機器人坐標系，如圖2所示。其中靜坐標系O0-X0Y0Z0固定在機架上，關節連接處建立各動坐標系，其中Zi軸均沿關節軸線方向，Xi定義為由Zi-1軸指向Zi軸方向。

圖1 碼垛機器人三維示意圖

圖2 基于D-H參數法的碼垛機器人坐標系

構件結構參數以及理論值如表1所示，其中q1、q2、q3、q4分別表示腰座、大臂、小臂、手腕體四個驅動關節處的轉角，同時。

表1 機器人各構件結構參數及其理論值

根據D-H建模法得末端抓手位姿矩陣為：

末端抓手靜坐標系下位姿向量N為：

2.2 碼垛機器人誤差模型

碼垛機器人各構件的加工、裝配誤差，機械傳動誤差等因素會導致各構件運動變量與結構參數產生誤差，即：，進而最終影響末端手腕體的位姿誤差。

相鄰兩構件之間的姿態變化矩陣對各結構參數的偏導，即位姿變換矩陣對θi、αi、ai、di偏導數為：

設ki1、ki2、ki3、ki4分別表示碼垛機器人各構件的運動變量和結構參數碼垛機器人末端的位姿矩陣對于kij（i=1，2，3，4，5；j=1，2，3，4）的偏導數可以表示為：

在靜坐表系下的位置姿態誤差，可以用向量ΔN表示：

上式中，Δx、Δy、Δz為位置誤差，Δα、Δβ、Δγ為姿態誤差。結合姿態變化矩陣的偏導函數式(7)可得，位置誤差函數與姿態誤差函數：

至此，便得到了碼垛機器人誤差模型，基于碼垛機器人誤差模型可以對機器人各結構參數與運動變量的誤差對機器人末端姿態誤差的影響進行分析。

2 碼垛機器人靜態誤差分析

本文重點研究零件制造、安裝、機械傳動誤差造成的影響。暫不考慮重力、溫度造成的零件變形誤差與控制系統誤差。在分析碼垛機器人靜態誤差時假設機器人各構件均是純剛體，忽略構件柔性與關節柔性對于末端變形的影響。本文主要考慮由于腰座、大臂、小臂、手腕體的加工、裝配以及機械傳動等因素造成的誤差。此外姿態保持架與大臂連桿1和大臂連桿2的加工與安裝誤差也會造成末端位置姿態誤差產生影響，本文重點考慮由于姿態保持架及相應連桿加工與安裝誤差對末端造成的平面度誤差Δβ。

2.1 機器人末端位置誤差分析

腰座、大臂、小臂、手腕體的加工、裝配以及機械傳動等因素造成的機器人末端位置誤差，主要體現在各構件結構參數與運動變量參數誤差造成的機器人末端位置誤差。在各構件結構與運動變量參數一定的情況下，隨著驅動關節角度變化，機器人末端位置誤差也會隨之變化。因此本節主要研究固定位姿下各構件結構參數與運動變量參數的誤差對末端位置誤差的影響，以及在結構參數與運動變量參數誤差一定的情況下隨著機器人驅動關節（大臂、小臂驅動關節）角度的變化，機器人末端誤差的變化規律。

1）考慮各構件結構參數與運動變量對末端位置誤差的影響。

首先給定碼垛機器人位姿，設大臂驅動關節轉角為45°，小臂驅動關節轉角為135°，腰座驅動關節轉角為0°。本文研究中為單一變量的誤差對機器人末端位置誤差的影響。

考慮腰座與機架關節處的3個結構參數α1、a1、d1與1個運動變量參數θ1存在的誤差對末端位置誤差的影響。首先分析腰座與機架關節處加工誤差造成的a1與d1對末端位置誤差的影響，如圖3所示，其對末端位置誤差沒有放大效應，只是單純的等比例誤差影響。其次考慮由腰座加工與裝配過程中產生的同軸度誤差引起的Δα1以及腰座驅動關節誤差引起的Δθ1對末端位置誤差的影響，如圖4所示。

圖3 Δa1、Δd1對末端位置誤差的影響

對于大臂與腰座關節、大臂與小臂關節、小臂與手腕體關節、手腕體與抓手關節處存在的其余16個結構與運動變量參數αi、ai、di、θi（i=2，3，4，5），在的其余16個結構與運動變量參數αi、ai、di、θi（i=1，2，3，4）對末端位置誤差的影響，其分析方法與α1、a1、d1、θ1相同。限于文章篇幅有限，只分析某些對末端誤差影響較大的參數。

圖4 Δ1θ、Δ1α對末端位置誤差的影響

腰座與大臂關節處，由于腰座加工與腰座、大臂裝配過程產生的同軸度誤差a2、Δθ2經大臂、小臂桿件放大作用后，對機器人末端位置Y軸方向誤差產生較大影響，其影響規律如圖5所示，對X軸與Z軸方向誤差影響非常微小。由于腰座加工誤差造成的a2與d2對末端位置誤差沒有放大效應，只是單純的等比例誤差影響。

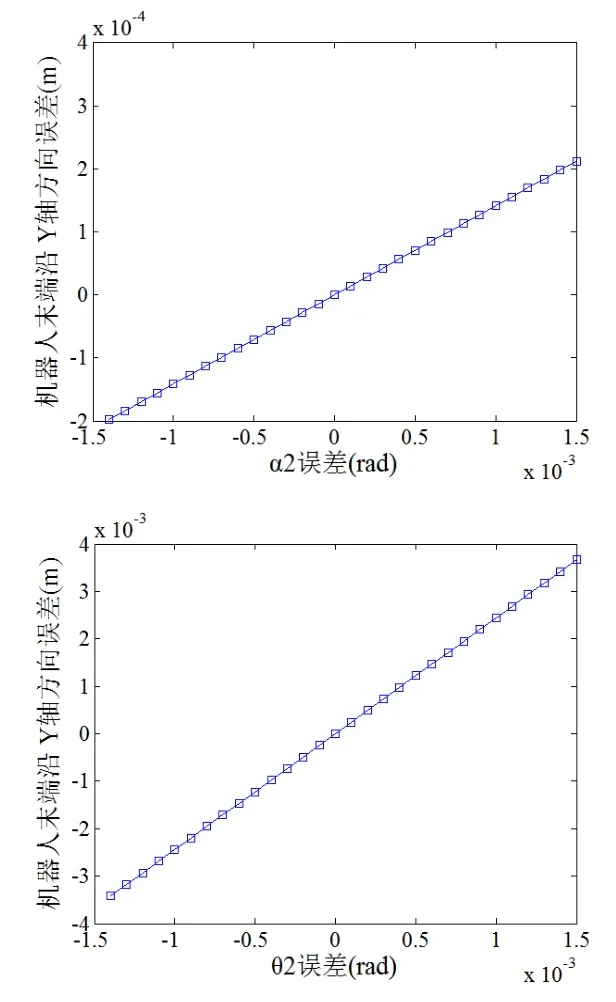
圖5 Δ2α、Δ2θ對機器人末端沿Y軸方向誤差的影響

對大臂與小臂關節處，大臂與小臂關節處由于大臂加工過程與大臂、小臂裝配過程產生的同軸度誤差a3經小臂桿件放大作用后，對機器人末端位置Y軸方向誤差產生較大影響，如圖6所示。大臂與小臂關節處的運動變量誤差（驅動關節產生的誤差）Δθ3經小臂桿件放大作用后，對機器人末端位置X軸與Z軸方向誤差均會產生一定的影響，如圖6所示。大臂加工誤差造成的d3對末端位置誤差沒有放大效應，只是單純的等比例誤差影響。

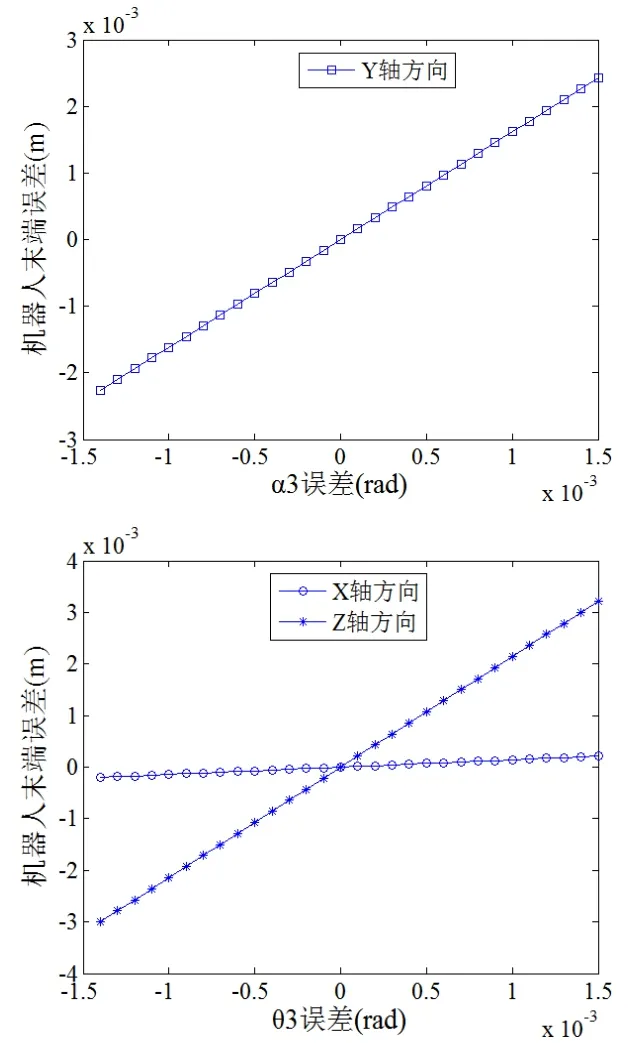
圖6 Δ3α、Δ3θ對機器人末端誤差的影響

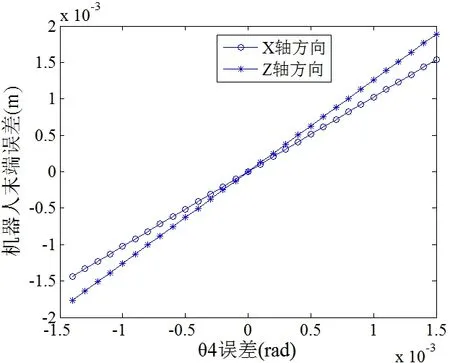
圖7 Δ4θ對機器人末端誤差的影響

考慮手腕體與抓手關節處的3個結構參數α5、a5、d5與θ5對末端位置誤差的影響。由手腕體與末端抓手連接處加工誤差引起的a5與d5對末端位置誤差沒有放大效應，只是單純的等比例誤差影響。由加工過程與裝配過程中產生的同軸度誤差引起的a5與Δθ5對末端位置誤差很小，此處不再討論。

2）考慮各驅動關節轉角對末端位置誤差的影響：

在各構件結構參數誤差一定的情況下，考慮不同位置（各驅動關節轉角不同）時，末端誤差隨驅動關節轉角的變化規律。給定各構件結構參數誤差：設ai、di的位移誤差為0.05mm，設iα、θi的角度誤差為0.5°。碼垛機器人四個驅動關節中，腰座與手腕體驅動關節轉角變化對末端位置誤差沒有影響。大臂、小臂驅動關節轉角對末端位置沿Y軸方向誤差影響成簡單的線性關系，即隨著碼垛點距離機架位置越遠，其末端位置沿Y軸方向誤差越大；大臂小臂驅動關節轉角變化對末端位置沿X軸與Z軸誤差影響較為復雜。其影響規律如圖8所示。

圖8 大臂與小臂轉角對末端位置誤差的影響

由圖8可以看出，在小臂轉角一定時，隨著大臂轉角q2從0rad到2.4rad變化，末端Z軸方向誤差先增大后減小，X軸方向誤差線減小后增大；在大臂轉角一定時，隨著小臂轉角q3從0.6rad到3.2rad變化，末端Z軸方向誤差先一直減小，X軸方向誤差線增大后減小；碼垛機器人在大小臂運動過程中，其末端Z軸方向最大誤差為7.68mm，其末端X軸方向最大誤差為3.85mm。

2.2 機器人末端姿態誤差分析

1）主要構件結構參數與運動變量誤差對末端姿態誤差的影響

由腰座加工與裝配過程中產生的同軸度誤差引起的Δα1，會對機器人末端沿X軸轉動方向產生等效的誤差Δα，對機器人末端沿Y軸與Z軸轉動方向誤差沒有影響，如圖9所示。由腰座驅動關節誤差引起的Δθ1對末端位置誤差的影響會對機器人末端沿Z軸轉動方向產生等效的誤差，對機器人末端沿X軸與Y軸轉動方向誤差沒有影響，如圖9所示。

在以改善生存條件和促進轉型發展為特征的一系列試點示范基礎上,隨著我國經濟社會發展和社會福利改進需求的調整,我國可持續城市建設逐漸從關注生存環境、經濟轉型發展等議題向關注社會的公平、人的發展公平以及社會與環境的協同發展方向轉型,可持續城市關注的議題更加綜合，更注重人與社會、人與自然、社會與自然的協調發展。

圖9 Δ1α、Δ1θ對機器人末端姿態誤差的影響

對于大臂與腰座關節、大臂與小臂關節、小臂與手腕體關節、手腕體與抓手關節處存在的其余8個結構與運動變量參數ai、θi（i=2，3，4，5）對末端姿態誤差的影響，其分析方法與a1、θ1相同。

2）姿態保持架系統造成的姿態誤差

碼垛機器人結構簡圖，如圖10所示。平行四邊形ABFI與平行四邊形BCDE的作用是保持手腕體下表面始終與地面平行。因此姿態保持架與姿態保持桿的加工與安裝誤差會造成的末端手腕體的平面度誤差，即β。另外，姿態保持架與相應連桿的加工與安裝誤差也會對a、產生一定影響，因其影響較小，本文暫不考慮。

圖10 機器人結構簡圖

考慮大臂連桿2與腰座連接處的I點加工位置或者安裝位置誤差對于手腕體末端平面度誤差的β影響：設I為理論坐標點，設加工或者裝配過程造成I點產生誤差到I’點，根據桿長不變原理，可以求得F點的坐標：

由F點與B點坐標可以求解姿態偏差角：

上式中：θ表示AI連線與X軸的夾角（銳角）。

同理，可以求解由于F、E、D點處的加工位置或者安裝位置誤差對于手腕體末端平面度誤差的β影響。

3 重力對機器人末端誤差的影響

在前面分析機器人靜態誤差時，為了方便分析桿件單一結構參數對機器人末端位置姿態誤差的影響，并沒有考慮桿件以及關節的柔性。工程實踐表明，碼垛機器人在大負載情況下，重力造成的末端位置誤差較大，不可忽略，因此本節重點研究重力造成的末端誤差。在研究重力對碼垛機器人末端誤差的影響時，將機器人桿件作為柔性桿件，并且考慮驅動關節的柔性。

由碼垛機器人整機運動微分方程[8,9]可得，靜態下（各驅動關節角速度、角加速度為零）機器人在重力作用下的變形可以表示為：

其中：[K]表示291×291的系統剛度矩陣；{q}表示291×1的系統節點彈性位移；[G]表示系統所受的重力；

在重力作用下，碼垛機器人末端沿靜坐標系X軸方向誤差以及沿Z軸方向誤差可以表示為（設腰座驅動關節轉角位零）：

上式中：{q}67表示系統節點廣義坐標系第67個坐標的彈性位移；{q}69表示系統節點廣義坐標系第69個坐標的彈性位移；

碼垛機器人系統剛度矩陣是與大臂、小臂轉角有關的函數矩陣，系統剛度矩陣會隨著大臂與小臂轉角的變化而變化，即機器人在重力作用下末端誤差會隨著大臂與小臂轉角變化而變化。在給定機器人各構件參數下，結合式(13)與式(14)可以求得不同驅動關節轉角時，重力對末端位置誤差的影響。隨著大臂轉角、小臂轉角的變化，重力對機器人末端沿靜坐標系X軸方向與Z方向的誤差影響如圖11所示。

由圖11分析可知，在大臂轉角一定時，隨著小臂轉角的增大，機器人沿Z軸方向誤差先增大后減小；沿X軸方向誤差，在機器人末端達到最遠點之前，隨著小臂轉角的增大而增大，達到最遠點之后，隨著小臂轉角的增大，沿X軸方向誤差先減小后增大。

圖11 重力造成的末端誤差與大臂、小臂轉角之間的關系

4 結論

本文主要對碼垛機器人誤差進行了分析，基于D-H參數法建立了碼垛機器人誤差傳遞函數；對機器人靜態誤差進行分析，重點研究了各構件結構參數對末端位置誤差的影響，并對末端位置誤差與關節轉角的關系進行了分析。對機器人末端姿態誤差，進行了研究，并對主要構件造成的誤差影響進行了分析與討論；建立了碼垛機器人大臂、小臂靜態驅動動力數學模型。對重力造成的末端誤差，尤其是重力影響下導致大臂、小臂驅動關節轉角誤差對末端位置誤差的影響進行了分析。為對應誤差補償提供了理論基礎。