全方位移動機器人控制系統設計

（南京工程學院，南京 211100）

0 引言

隨著倉儲物流業、生產制造業智能化的不斷發展，人們對運輸機器人需求越來越大。全向移動機器人因具備在狹小空間的作業能力，且具有靈活多樣的運動姿態，受到人們的廣泛關注，其中Mecanum輪機器人是研究最早、應用最廣泛的。Mecanum輪最早由瑞士工程師Bengt Iron于1972年發明。隨后卡內基.梅隆大學的Muir PF等基于矩陣變換法建立了運動學模型，成功地應用在了車輪滑動的檢測和航位推算上[1]。L.Gracia采用對機器人動力學逐次近似的方法得到了考慮車輪打滑的運動學模型，為提高Mecanum輪機器人控制精度、解決打滑問題建立了理論基礎[2]。劉磊設計了一種全向移動機器人控制方法，通過對機器人和電機模型的仿真解算反解出機器人的實際導航參量，用于機器人的導航位姿閉環控制[3]。

由于Mecanum輪由輥子組成，靠輥子的摩擦力相互作用產生運動，容易發生側滑造成運動精度相對較低。輥子α角的實際值與理論值也存在一定的偏差，直接影響到機器人的速度及運行軌跡[4]。針對此問題，本文設計了基于PD的全方位移動機器人控制系統，通過PD調節減少機器人的實際速度和預定速度之間的誤差，保證其運動精度，最后通過實驗驗證系統設計的效果和控制精度。

1 全方位移動機器人運動學建模

Mecanum輪由輪轂和安裝在輪轂外緣上的一組輥子組成，輥子軸線與輪轂軸線成一定角度，并且輥子可繞自身軸線旋轉。使用Mecanum輪的機器人可以在狹小作業空間里行進自如，不需要較大的轉彎半徑。通過車輪的組合使用和各車輪轉動速度和方向的協調控制，可以使車體沿著平面內的任意方向移動和轉動[5]，可大大提高運輸效率。

全向移動機器人的車輪布局如圖1所示。設機器人的廣義速度為（υx，υy，ωz）T，（ω1，ω2，ω3，ω4）T表示各輪的轉速。輥子軸線與輪轂軸線的夾角為α，機器人的半車長和半車寬分別為a、b，車輪半徑為R。

圖1 全向移動機器人車輪布局

根據運動學分析，Mecanum輪機器人的正運動學方程為：

其中：L=b+acotα。此次設計機器人采用的Mecanum輪α角為45°。從式(1)可得，賦予四個輪子不同的轉向和轉速就可以實現機器人向任意位置和方向運動，這是控制全向移動機器人的理論基礎。

2 運動控制系統硬件設計

本設計采用以STM32F103ZET6控制芯片[6]為核心的控制器，其高級定時器和通用定時器具有正交編碼計數、產生四路獨立PWM波功能，具有豐富的內、外設資源，滿足本系統對多路電機的控制和轉速采集要求。系統總體結構如圖2所示。控制模塊產生PWM波，通過驅動器驅動直流電機，電機經減速器傳動后驅動4個Mecanum輪。霍爾編碼器與控制器相連，用于測量電機轉速。使用紅外遙控器進行控制指令的發送。帶有電池保護板的12V電源為電機供電，經變壓模塊調壓后為控制模塊、霍爾編碼器等控制電路供電。

圖2 控制系統基本組成

3 運動控制系統軟件設計

3.1 PD控制模型

本文采用增量式PD算法，設計方案如圖3所示。PD算法完整定義為u(k)=KPΔe(k)+KD[Δe(k)-Δe(k-1)][7]，其中，u(k)為第k次采樣時刻控制器的輸出；e(k)為第k次采樣時刻輸入的偏差；KP為比例系數，主要作用是對系統出現的誤差做出快速響應；KD為微分系數，主要作用是給出預調量提升系統動態特性。具體思想是將閉環系統反饋回來的實際運行速度與給定的目標運行速度進行比較，并將速度誤差作為輸入量送入PD控制器中，經過控制器的比例、積分運算得出相應的誤差補償值，再將補償過的控制信號送入被控對象進行控制。

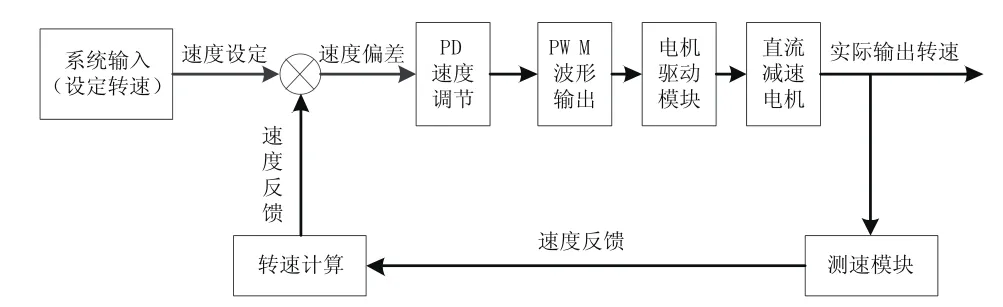
圖3 PD控制設計框圖

3.2 程序設計

本文設計的控制系統程序采用模塊化設計，由系統初始化程序、PD算法程序、正交編碼測速程序、運動控制程序、定時器程序、PWM脈寬調制程序等組成，程序流程如圖4所示。根據運動學模型編寫運動控制程序。機器人運行時，首先進行系統初始化，包括定時器、串口函數、延時函數、PWM函數的初始化，接著開啟內外部中斷。當接收到控制指令時，STM32F103ZET6控制芯片產生四路獨立的PWM信號，運行控制程序，此時機器人將按期望的方向和速度運動，可通過控制器進行加減速和換向控制。電機位置的變化引起霍爾信號變化，定時器的正交編碼計數功能將計15ms內電機脈沖總數，輸入到PD算法計算實際轉速，與設定轉速比較后，輸出新的PWM占空比，重新對電機調速，在定時周期內不斷進行該步驟，使其與預定轉速相同，保證機器人的直線運動精度。

圖4 機器人運動控制系統程序流程

4 電機調試

本文設計了四輪結構的Mecanum輪機器人，如圖5所示。外形尺寸為390×380mm，車輪半徑為100mm，沿y軸最大運行速度為1.2m/s。采用12V直流減速電機，額定扭矩1N·m，提供輸出軸每轉663個反饋的脈沖信號，為提高控制精度，脈沖信號的上升沿和下降沿均計數。電機調試時預設速度為電機在15ms周期內走過40個脈沖數。建立控制芯片的串口與PC串口之間的通信，可將機器人在設定周期內的速度值發送到PC保存并繪制PD速度響應曲線。

對機器人的1號電機采用PD閉環控制，不斷調整閉環模型的參數，當取KP=65，KD=90時，電機具有較好性能。閉環后的速度相應曲線如圖6所示，此時超調量是10%，調節時間0.33s，穩態誤差2.5%，0.33s之后電機的實際速度與設定速度大致相同。對機器人2、3、4號電機進行調試，超調量均低于15%，調節時間0.33s以下，穩態誤差控制在2.5%，結果匯總如表1所示。

圖5 全向移動機器人實體

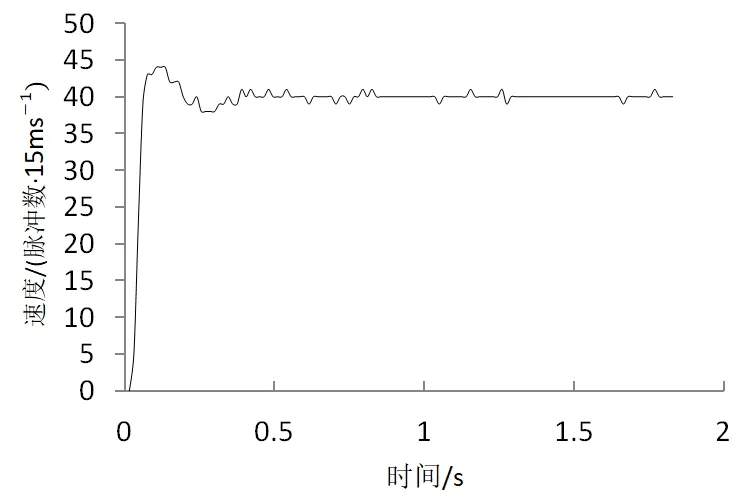
圖6 電機1實際環境PD響應曲線

表1 電機1、2、3、4號電機調試結果

5 運行軌跡實驗

電機調試完畢后，將機器人放置在工業攝像頭下進行運行軌跡記錄實驗。參照機器人車輪布局圖，規定機器人運動時沿Y軸正方向為前進，沿X軸正方向運動為右平移，以原點為圓心順時針轉動為右旋轉，沿45°角方向為右前進。相機可視的像素坐標范圍為600×500，轉換為實際坐標為300×250cm，圖像采樣頻率為0.1s/次，實驗前設置好軌跡記錄點和理想軌跡點，建立攝像頭與PC機之間的數據傳輸，記錄機器人的運動情況，軌跡信息將以坐標形式保存。圖7為前進、右平移、右前進的軌跡圖及局部放大圖，圖8為原地右旋轉軌跡圖及局部放大圖。

圖7 三種典型運動方向軌跡

圖8 原地右旋轉運動軌跡

表2 四種運行狀態數據分析

由實驗數據作圖并分析，前進時最大誤差為0.854cm，實驗記錄距離為300cm。右平移時最大誤差為0.753cm，實驗記錄距離為250cm。右前進時最大誤差為1.632cm，實驗記錄距離為347cm。前進、右平移、右前進、右旋轉的實際軌跡的坐標點與理想軌跡之間的標準差分別為0.62、0.54、1.13、0.36，匯總如表2所示。由運動時的最大誤差及實際軌跡的坐標點與理想軌跡之間的標準差可知，該控制系統在一定程度上保證了機器人的直線運動精度和原地旋轉精度，其中右前行進時直線精度相對較差。

6 結束語

本文開發設計了全方位移動機器人并設計了其運動控制系統，運用PD閉環控制方法，通過調節KP、KD參數，得到了較為理想的速度響應曲線，使機器人能夠較為準確的按程序給定的速度和方向運行，保證了機器人運行的直線精度，實現了Mecanum輪機器人的運動控制。

在實驗過程中，發現此控制系統仍沒有達到最理想狀態，其可能原因是機器人本體設計時的機械公差、輪體打滑、負載不均勻、霍爾傳感器精度等因素的影響，而且本文的PD控制方法只在15ms周期內進行計算，還可在更短的采樣周期內進行閉環控制，盡量提高控制算法的實時性。在今后的研究中，將對機器人進行動力學建模并設計控制算法，實現更加精確的控制。