煤層氣達西、非達西滲流理論和擴散理論的研究進展綜述

彭英明，邵先杰，李 鋒，李明峰，劉澤恒，OYAKA Dickens

(燕山大學 石油工程系，河北 秦皇島 066004)

煤層氣又稱煤層甲烷是成煤母質在煤化過程中形成并儲集在煤層中，以CH4為主的非常規天然氣，其中甲烷含量一般大于80%，甚至可達到98%[1]。同時煤層氣也是一種有害氣體，不僅對煤礦生產安全造成了威脅，還具備嚴重污染環境的能力。因此，研究煤層氣各個階段的流態特征對減少瓦斯爆炸存在的安全隱患、改變能源供給以及保護環境都有重要意義。

煤層是一種具有雙重孔隙度和雙重滲透率的儲層，煤層氣主要以游離氣、溶解氣和吸附氣賦存于煤層中。煤層氣在煤層中的賦存狀態、煤基質的組分和結構特征決定了煤層氣的運移過程為氣體在煤基質中的解析—擴散和在裂縫系統中氣體的滲流[2]。

1 滲流理論及其研究進展

1883年英國物理學家雷諾通過大量實驗對流體流動狀態判識，從而使分析流體問題簡單化[3]，此后國內外學者對流態問題進行了更為深化的研究，并把流態分布類型歸結為低速非線性滲流、線性滲流和高速非線性滲流[4，5]，而煤儲層作為一種多孔、低滲透介質，煤層氣在運移的過程中也必有這幾類流態特征[6]。

1.1 達西滲流理論

線性滲流區符合達西流要求，即裂隙中煤層氣的運移屬層流，流速與瓦斯壓力差成正比。

在20世紀40年代前前蘇聯科學家就將線性滲透定律—達西定律引入地下瓦斯的流動過程中，建立了關于吸附煤層瓦斯作用的瓦斯控制方程。在國內，最先將達西定律應用于煤層瓦斯流動的是周世寧院士[7]，他認為煤層瓦斯(沼氣)的流動基本上符合達西滲流定律，并根據氣體在多孔介質中滲流的理論將煤層瓦斯流動劃分為單向、徑向和球向三種類型。由于多數井下瓦斯的復雜流動可簡化為一維平行流動、徑向流動的無限和有限的流場或者是它們的組合。因此自20世紀80年代以來，瓦斯的滲流模型得到進一步修正與完善，1986年譚學術[8]等結合滲流力學理論和熱力學理論，將煤層瓦斯當做真實氣體，提出了礦井煤層真實瓦斯氣體的滲流方程，并對該方程進行簡化；1989年余楚新等[9]提出煤層中參與滲流的瓦斯量是煤體瓦斯含量部分量的觀點，在假設煤體中瓦斯吸附與解吸過程是完全可逆的條件下，建立起了煤層瓦斯滲流的控制方程；隨后孫培德[10-13]基于前人的研究成果較系統地闡明了新的煤層瓦斯動力學模型，其模型比國內外三大模型(周氏流動模型、(日本)樋口流動模型、(英國)Ediz和Edwards流動模型)更逼近實際，從而使線性滲透理論的數學模型和流動方程得到了完善。2010年楊寧波[14]以達西定律和煤層瓦斯流動理論假設為基礎，運用質量守恒定律，建立了鉆孔周圍煤體瓦斯流動的數學模型，得到了鉆孔周圍瓦斯流動的方程及其定解條件。

近年來，隨著計算機技術的發展，煤層氣流動規律的研究手段向數值模擬和有限元分析等方向轉變。1997年丁廣驤[15]利用守衡原理和達西定律建立了煤層瓦斯實用動力學方程，并給出其Galerkin有限元解法。同年，駱祖江[16]以菲克定律和達西定律為基礎，結合有關試驗資料數值模擬的方法進一步求得了氣—水二相滲流模型，為甲烷資源進一步開發提供了一系列數據，并在實際應用中取得了良好的效果。2004年肖遠見[17]將煤層中的瓦斯視為真實氣體，以達西定律為基礎建立滲流方程，并給出此方程的三維分析方法；根據數值分析結果，為沿層鉆孔預抽放瓦斯提供依據。

1992年羅新榮[18]為考證達西定律的適用性，實驗時維持孔隙平均壓力不變，測定了氣體流量與壓力平方差的關系，結果如圖1所示。實驗結果表明：在較低流速下，氮氣流量與壓力平方差符合直線關系，達西定律成立。

圖1 試驗氣體CH4流量與壓力平方差的曲線

由于達西實驗本身的條件限制，達西定律有三個基本的限定條件：滲流流體為單相牛頓流體，服從牛頓內摩擦定律；多孔介質穩定且與流體之間的相互作用對流體流動影響小；流體以層流狀態流動。因此煤層內瓦斯的雷諾數范圍也成為研究煤層氣滲流的熱點。目前學者們大多認同雷諾數小于1～10某一數值的層流才符合達西定律。但也有學者[19]經過實驗發現即使雷諾數在1～10的條件下，達西定律仍不適用。從而原有的線性滲流理論在生產實踐中的應用受到很大限制。

1.2 非達西滲流理論

線性流動理論只適用于雷諾數在線性層流區這個范圍，而超出這個范圍后將不符合達西定律。多孔介質中可動氣體運移呈現出低速非達西滲流特征應具備儲層滲透率低甚至特低和儲層中應含有一定程度的水兩個條件，而我國煤層滲透率普遍偏低且含水飽和度較高，因此我國煤層氣開采時大多都會出現低速非達西滲流現象[20]。

非線性滲流理論首先應用于單相液體，首先發現瓦斯非線性滲流的是E M Allen，當他進行均勻固體(煤樣)中瓦斯涌出實驗時，發現實驗結果并不符合達西定律。1984年日本學者通過變化壓差測定煤樣瓦斯滲透率時發現瓦斯流動規律與達西定律不相符，并在大量試驗研究的基礎上提出了冪定律。該理論的實質是瓦斯流動速度和瓦斯壓力梯度的m次冪成正比，其適用范圍主要為雷諾數在10～100之間的非線性層流區。隨后孫培德[21]通過非均質多孔介質水動力學理論將冪定律進行了推廣，并建立了具有可壓縮性的煤層氣在煤層中的非線性流動模型。1991年羅新榮[22]提出考慮克氏效應的修正形式非線性煤層氣滲流規律，并建立了相應的瓦斯流動數學模型并指出達西定律的使用范圍。然而，隨著研究的深入和實驗條件的限制，對非線性瓦斯流動理論也產生了爭議，1994年劉明舉[23]認為文獻[21]由于模型的錯誤，無量綱過程的錯誤，其所得的數值結果是不可靠的，在冪定律基礎上導出的煤層瓦斯流動模型存在一定問題，文章最后導出了瓦斯流動遵循冪定律時的正確流動模型。

近些年來Liu等[24]用Lattice Boltzmann方法模擬了氣體滲流產生的滑脫效應并得到了較好的物理解釋。2006年鄧英爾等[25]將實驗理論與計算相結合并對大量實驗數據進行分析，提出了低滲透孔隙—裂隙介質氣體非線性滲流運動方程，借以描述含瓦斯煤的滲流特性。但該方程中較為復雜且描述含瓦斯煤滲透阻力的物理內涵不明確，因而應用范圍受限。隨后國內學者[26-28]結合理論假設，通過含瓦斯煤的滲透率的測定的實驗，認為當煤層內瓦斯壓力梯度小于某一值時，瓦斯在煤體內為擴散狀態。張志剛[29，30]認為前人模型主要采用唯象學方法，根據非線性滲流的物理現象擬合出數學方程，難以反映造成瓦斯在煤體內非線性流動的內在原因與影響因素。而且實驗方法存在一定問題，由于煤樣在實驗中承受了額外的壓力煤與瓦斯氣體分子間吸附作用的存在，從而導致了氣體測試時產生誤差，因此他提出了密封缸套結合密封試劑的方法。基于力學平衡方程，建立了描述瓦斯氣體滲流特征的非線性滲流方程，定量描述了產生非線性滲流的內在因素。

國內學者研究表明[31]，完整的低滲儲層滲流應該如圖2所示。

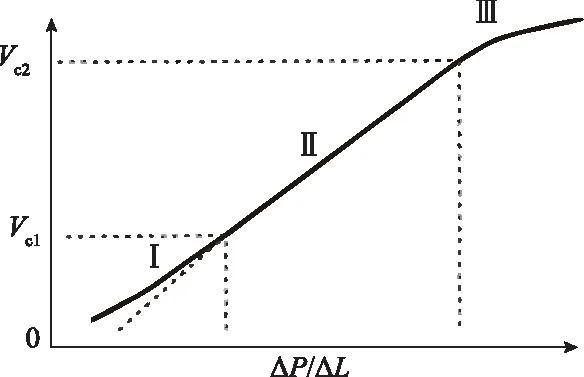
圖2 非線性滲流特征圖

Ⅰ(非線性段)：在低壓力梯度范圍內，滲流曲線為非線性，滲流量隨著壓力梯度的變大而變大。Ⅱ(擬線性段)：在較高壓力梯度下，滲流曲線呈擬線性。擬線性段的反向延長線不通過坐標原點，而與壓力梯度的軸有正值交點。Ⅲ(非線性段)：高產條件下高速非達西階段。然而與國外煤層相比，我國煤層滲透率普遍低甚至特低，含水飽和度較高，儲層具有低壓、低滲、低孔特征，因此在開采過程中的氣體滲流普遍呈現低速非達西滲流特征，極少出現高速非線性滲流。其中臨界點及臨界壓力梯度：非線性段過度到擬線性段的點稱為臨界點C。臨界點所對應的壓力梯度為臨界壓力梯度，滲透率越低臨界壓力梯度越大，非達西滲流特征越明顯。

現有低速非達西滲流的運動方程僅僅是通過實驗數據擬合得到的，其產生機理各個學者都有不同的意見，還沒有形成統一的意見，對于非線性滲流的模型學者們還是較多青睞于冪定律。因此對于非線性的達西定律基礎上的瓦斯流動理論的深入研究是當下探索的重點方向。

2 擴散理論及其研究進展

分子運動論認為任何物質都不停的在做不規則運動；擴散是指某種物質的分子通過不規則運動、擴散運動而進入到其他物質里的過程；氣體擴散是指某種氣體分子通過擴散運動而進入到其他氣體里；因為氣體分子的不規則運動比較激烈，所以擴散比較明顯。而煤作為一種典型的多孔介質，對于煤層氣的擴散模型，人們普遍認為由于濃度差的作用使解吸氣從基質孔隙擴散到裂縫中，進而在壓差的作用下從裂縫滲流到生產井[32]。

2.1 線性擴散理論

線性擴散理論主要是以菲克擴散定律為基礎建立的煤層氣擴散理論，擴散體系中的甲烷由高濃度向低濃度運動，擴散速度與流體的濃度梯度呈線性正比關系。

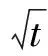
當孔隙直徑遠大于孔隙氣體分子的平均自由程，這時孔隙氣體分子的碰撞主要發生在自由孔隙氣體分子之間，而分子與納米級孔壁的碰撞機會相對較少，該類擴散符合菲克定律，用于描述瓦斯在煤儲層中從煤基質孔隙表面上解吸的氣體運移到割理系統的主要過程。煤炭科學研究總院撫順分院[36]用解吸法確定煤層含量時常用的經驗公式來進行了實驗，即：

Qt/Q

式中，d為煤屑直徑；D為擴散系數；Qt為擴散時間為t時累計的瓦斯擴散量；Q∞為表示時極限瓦斯擴散通量；t為時間；K為校正系數。

對陽泉一礦六種不同粒度的煤樣進行了擴散速率的確定，在圖3中顯示了同粒度煤樣的測定結果。該實驗表明：瓦斯流動遵循擴散定律。

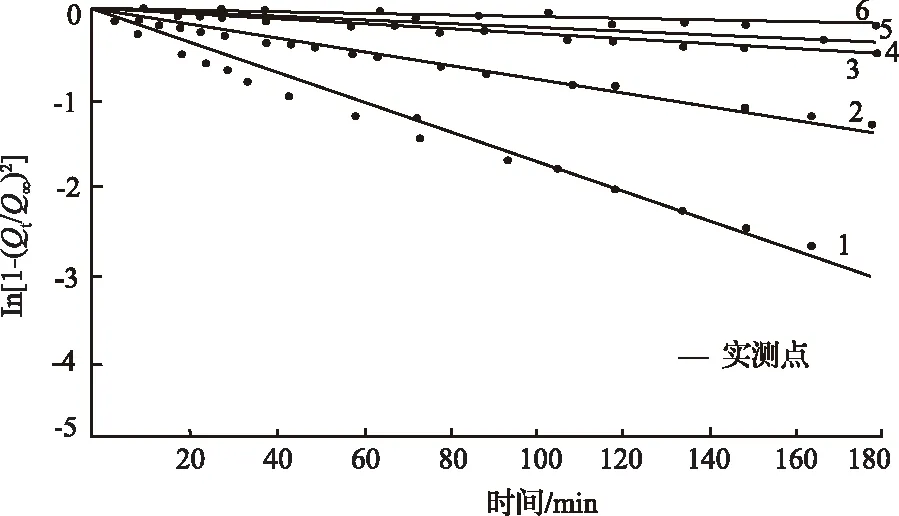
圖3 陽泉煤樣瓦斯擴散規律實測值

菲克擴散模型因物理意義明確，計算簡單，理論上具有寬廣的外延性，是整個擴散理論體系的基礎，一直沿用至今，為我國學者研究煤屑瓦斯擴散理論奠定了基礎。但該種假設是基于煤屑屬一種理想的吸附劑，即煤屑放散瓦斯的過程中，煤屑的孔隙結構未發生改變，但由于煤自身孔隙結構的特性有別于理想吸附劑，因而該種假設在諸多情況下勢必與實際不符，這便啟發了其他煤屑瓦斯擴散理論研究的發展。

2.2 滲透與擴散理論

一些學者經過多次實驗模擬研究發現基于菲克定律的定常數擴散系數的經典擴散模型與實際存在很大偏差，進而提出了瓦斯滲透與擴散理論：瓦斯煤層內瓦斯的運動是包含了滲透與擴散的混合流動過程。

1988年外國學者[37]依據菲克定律和達西定律，分別提出了煤塊瓦斯擴散方程和瓦斯滲流方程，并將其耦合成瓦斯滲透-擴散的流動方程，然后結合邊值條件，提出了瓦斯滲透-擴散的動力模型，并進行了數值模擬。1990年周世寧[38]院士結合對文獻[18]和文獻[36]的實驗結果，認為在煤體的大孔和裂隙中，瓦斯流動遵循著達西定律，而在微孔結構中，服從于擴散定律，所以其數學模型應該是以菲克定律與達西定律為基礎導出的聯立方程。1994年吳世躍[39]通過建立在實驗以及二相傳質理論基礎之上的假設，建立了考慮煤的壓縮性、結構特性、吸附游離瓦斯流動的差異和他們之間的關系的煤層瓦斯擴散滲透的物理數學模型。近年來，張鈞祥等[40]考慮了煤體孔裂隙多重介質特性、孔隙壓力、吸附膨脹效應，并結合彈性力學考慮了煤體的變形，共同構建能夠描述瓦斯擴散-滲流運移機理的耦合模型，隨后根據壓降法原理在現場測定了煤層內瓦斯壓力的變化，如圖4所示。

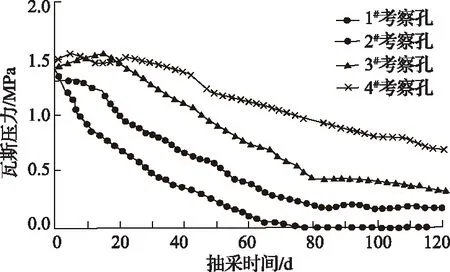
圖4 瓦斯壓力變化圖曲線

將模擬結果與壓降法現場實測結果進行對比分析，見表1，可以發現其模擬數據與現場實測數據基本吻合，說明該模型能反映煤層內瓦斯流動情況及鉆孔抽采有效半徑的變化規律，從而驗證了滲透與擴散理論的可靠性。

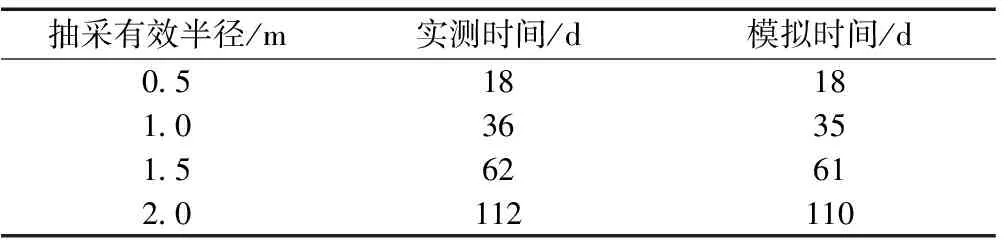
表1 實測結果與模擬結果對比分析

煤層中存在相互溝通的裂隙網絡，沿著這些裂隙網絡，游離瓦斯沿著這些裂隙流向低壓工作面，而煤體的滲透率與該裂隙網絡密切相關；同時煤塊內部的瓦斯解吸后向裂隙擴散[41]，因此煤層中瓦斯的滲透率和介質的擴散性共同決定了瓦斯的流動狀況。

2.3 考慮多種因素影響的非線性擴散理論

隨著人們對煤層氣擴散機理的進一步認識，發現由于不同條件下各種因素對煤層氣的擴散過程的影響，其瓦斯擴散模式并非僅為菲克擴散且擴散系數也并非為一定常參數。

1984年Smith[42]認為單孔模型存在一定缺陷，既而采用雙孔隙模型計算煤中瓦斯擴散，取得了比經典單孔隙模型更好的擬合精度，并根據煤的孔隙結構和氣體壓力的不同，認為煤層氣的擴散規律是體積擴散、克努森擴散和表面擴散的結合。近年來聶百勝和何學秋[43，44]在前人研究基礎上將瓦斯擴散歸結為菲克型擴散、諾森擴散、過渡型擴散、表面擴散和晶體擴散五種類型。其中，煤層氣的擴散以氣相擴散為主，表面擴散和晶體擴散量小。2008年閆寶珍等[45]結合前人研究成果，將煤層氣依據煤層氣的相態以及在煤體中不同的擴散位置，通過將煤層氣在煤層中的擴散分為氣相擴散、吸附相擴散、溶解相擴散和固溶體擴散，并研究出了煤納米級孔隙在儲層條件下的3種擴散模式的擴散系數具有相同的數量級。然而對于擴散系數的認識，很多學者認為擴散系數會因外界條件而發生變化。文獻[46，47]分別通過不同實驗驗證了甲烷的初始擴散系數均隨水分的含量增加而減少。謝策等[48]通過實驗探索溫度對煤粒瓦斯吸附特性的影響，其結果表明降低溫度可以減慢游離瓦斯的放散速度，其中低溫下溫度對煤、對甲烷的吸附的影響比常溫下的影響更明顯。劉彥偉和劉明舉[49]采用物理實驗方法探究了軟、硬煤粒瓦斯擴散系數，其實驗結果表明粒度大小影響軟、硬煤的的擴散初速度差值與擴散系數的比值。周市偉等[50]進行了擴散實驗，并結合擴散系數的新模型，從實驗數據得出了煤的變質程度和壓力均影響擴散系數的結論。李志強等[51]在保證壓力相同的情況下，對氣體的擴散量進行了不同溫度的試驗，其結果如圖5所示，通過計算不同溫度下的擴散系數，得到了擴散系數與溫度的關系，結果如圖6所示，該實驗表明了溫度對擴散系數有一定影響。

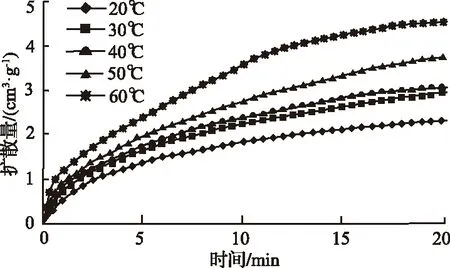
圖5 同壓吸附下不同溫度的恒溫擴散

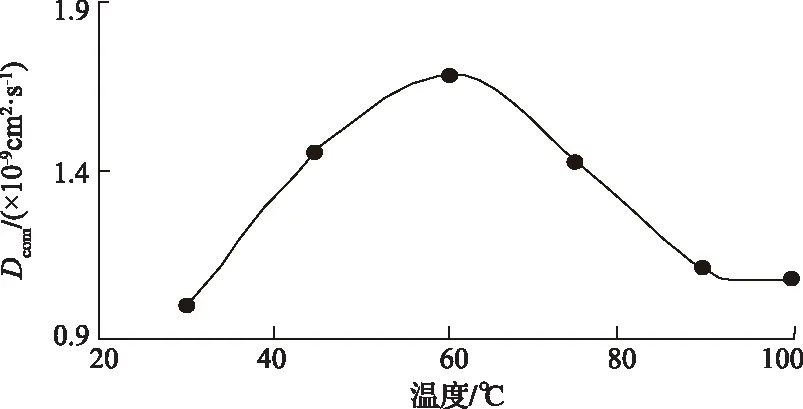
圖6 綜合擴散系數與溫度關系

擴散是一個非常復雜的過程，擴散速率會受到多種因素的影響。影響物質擴散的因素主要包含內在因素和外在因素。內在因素主要由擴散介質本身的特性決定，這些特性包括物質的組織、結構、化學成分等；外在因素主要與擴散相本身性質及所處的外部條件共同決定。

3 結論與展望

1)近些年來我國學者對煤層氣流態研究取得了顯著的進展，通過對煤層氣的達西滲流理論、非達西滲流理論、線性擴散理論、滲透與擴散理論和考慮多種因素的非線性擴散理論的大量實驗，對其進行了驗證，加深了我國在煤層氣開采過程中瓦斯流動規律的認識。

2)由于煤層內瓦斯運移是一個非常復雜的過程，這不僅與煤結構有關，而且受到眾多因素的影響，國內外學者在啟動壓力的非線性段、開采過程中擴散的作用、擴散系數的測定等方面很難達成共識，其次目前對煤層內的流態分布研究僅限于實驗室內，這與現場精確測試幾乎不存在可行性，所以對于煤層氣流態的研究還需進行更深層次的探索。

3)達西滲流理論和非達西滲流理論在近年來的快速發展得益于現代電子計算技術和數值模擬方法的普遍應用，地下滲流與擴散都是相當復雜的問題，因此在未來有必要進一步加強和發揮計算機技術在這些領域的作用；很多理論的模型都基于對實驗數據的擬合，因此在實驗儀器的精度方面還有待提高；部分理論模型較為復雜且實用性較低，因此模型應在簡潔與實用性方面加以改善。