一種大載荷量輕型無人機的總體方案設計與建模

黃 榮

（廈門大學嘉庚學院機電工程學院，福建 漳州363105）

0 前言

飛控系統的研發過程需要一個安全可靠的飛行平臺來進行飛行驗證。而無人機由于沒有人的約束，所以不僅可以具備有人飛機的特點以外，還可得到比有人飛機更多的設計自由度，而且可以用于執行人不便或不能完成的特殊任務。因此，設計一款適合于飛控研發試飛，且具有較大載荷量的輕型無人機具有很大應用前景。

1 總體設計

1.1 性能要求

綜合以往用于飛控研發的無人機性能，提出以下設計指標：

靜穩定飛機

設計最大起飛重量≤20 kg

設計空機質量≤10 kg

有效載荷≥3 kg

巡航速度≤75 km/h

最大平飛速度≤100 km/h

降落速度≤55 km/h

滿載起飛滑跑距離≤50 m

巡航高度≤120 m（考慮到國內無人機飛行安全法規，不做大升限設計）

起降方式：滑跑/彈射起飛，滑跑/降落傘降落

1.2 提出方案

結合研究的基本要求和以上的性能指標，提出以下初步設計方案：

（1）為了降低巡航速度和降落速度，需要提高整機的升阻比，優選高升阻比翼型；

（2）要降低飛機的起落距離就需要對機翼構型進行更為精細的設計，優化展弦比、機翼外形，使載荷分布更合理；

（3）為增大飛機橫側向與航向穩定性，選取較大的平垂尾尾容量；

（4）為了增大機頭空間，將發動機置于尾部或其他位置；

（5）考慮到發動機后置以及垂尾尾容量加大，故采用雙尾撐布局；

（6）為避免后置發動機螺旋槳滑流對平尾舵效的影響給飛控造成不必要的影響，故考慮移動平尾位置或其他構型尾翼。

綜上所述，本文將對大展弦比，雙尾撐后推式輕型無人機進行總體設計。

1.3 基本飛行任務剖面

飛行任務剖面，為完成某一特定飛行任務而繪制的飛機航跡圖形，是飛機戰術技術要求的組成部分和重要的設計依據，也是形象地表達飛行任務的一種形式[1]。如圖1所示即為本文所設計的輕型無人機的基本飛行任務剖面。

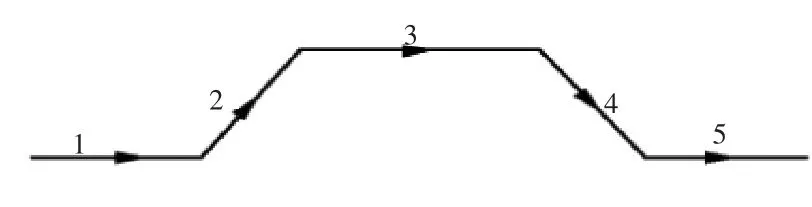
圖1 基本任務剖面

圖1 中各個階段為：1為起飛段；2為加速爬升段；3為巡航階段；4為減速下降階段；5為著陸階段。

1.4 總體布局

由以上提出的方案對飛機總體布局進行設計，飛機采用正常雙尾撐布局形式，該布局與常規固定翼類似，設計經驗和試飛經驗較多，且飛機重心在氣動焦點之前，符合靜穩定特性。

最終確定出本架輕型無人機的總體布局方案：

（1）發動機后置腰推形式，油/電兩用；

（2）采用雙垂尾形式；

（3）大展弦比平直、梯形機翼，綜合考慮當地飛行場地、車輛運輸以及國內“低小慢”航空器大致尺寸，設定翼展I=4 m；

（4）平尾位置布置于垂尾上部。

1.5 展弦比估算

本文所設計的輕型無人機屬于“低小慢”航空器范疇，飛行中的阻力主要來自壓差阻力和摩擦阻力，而摩擦阻力Cf與飛機外表面與氣流接觸的浸潤面積Sjr有關。

因為本文所設計的飛機為常規雙尾撐布局，又因目前此類“低小慢”航空器的設計準則不完備，故其浸潤面積比可以參考通用航空飛行器設計。

展弦比計算：取浸潤面積比

普通載荷量無人機等效展弦比λ=8，美軍“死神”無人機等效展弦比λ=20，展弦比太小會使得橫向穩定性減弱，而“死神”無人機展弦比太大，致使機翼承受的彎矩過大，因此本文設計的無人機展弦比先取兩者中間值14，故設等效展弦比

則又有浸潤展弦比

1.6 翼型選擇

翼型是構成機翼、尾翼的重要部分，它直接影響到飛機的性能和飛行品質[2]。

巡航高度取定100 m，巡航速度75 km/h，參考同級別其他無人機平均氣動弦長b≈0.35 m等參數下，此時雷諾數Re=500 000。

通常情況下，大彎度翼型被稱為高升力翼型，大彎度翼型擁有更大的最大升力系數[3]。根據以上數據和條件篩選翼型庫，擬定選擇AH-79-100B翼型，通過翼型模擬軟件對該翼型的曲線進行計算分析，結果如圖2、圖3所示。

圖2 升力、阻力系數曲線

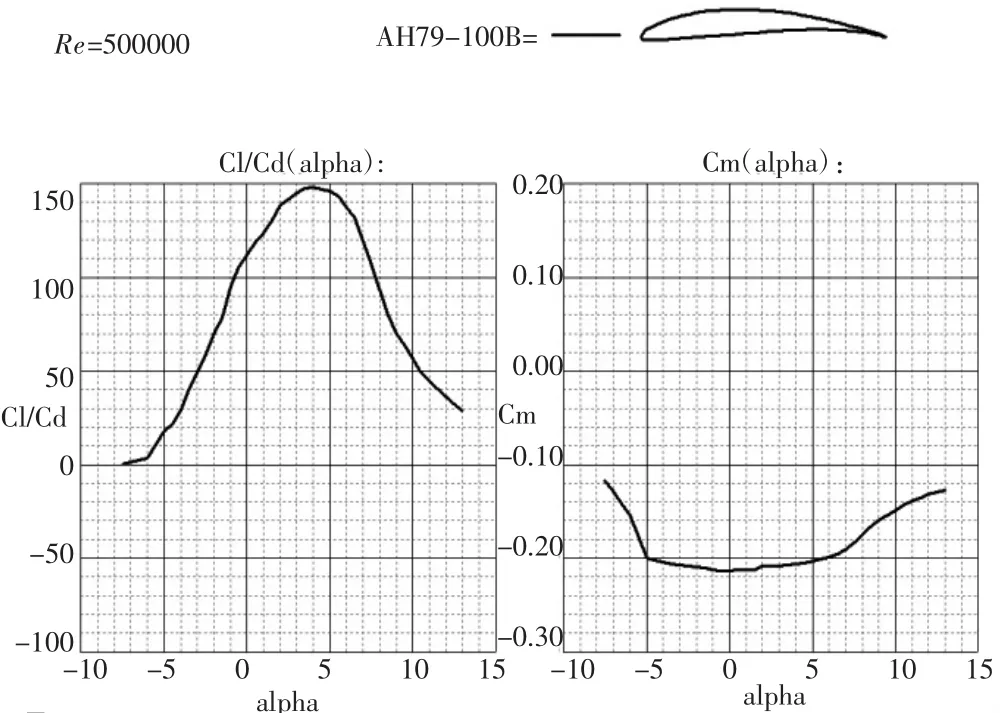
圖3 升阻比、俯仰力矩系數曲線

由圖3可知AH-79-100B翼型在Re=500 000情況下，總體上具有較高的升阻比和升力系數，且全范圍內曲線較平滑，無過大的激變，唯一的不足是俯仰力矩偏大，綜合考慮，決定選取AH-79-100B翼型。AH-79-100B翼型相對厚度為10.04%在30.9%的弦長處，相對曲面為6.42%在50%的弦長處。由圖2可知在迎角為13度時AH-79-100B翼型最大升力系數CLmax=1.76。

1.7 翼載荷的估算

飛機的翼載荷是指飛機重量m與機翼參考面積之比S，即m/S。通常重量都用正常起飛重量m0作為衡量的基準，而機翼參考面積S是指氣動力系數CL、CD等時用的機翼參考面積[4]。

（1）求失速速度

等效展弦比

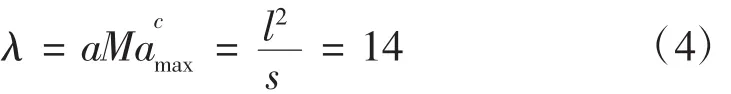
機翼平均氣動弦長

機翼展長

機翼面積

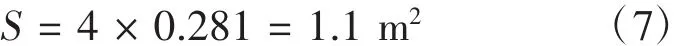
飛機總重

整機的最大升力系數一般為翼型最大升力系數的80%，則最大升力系數

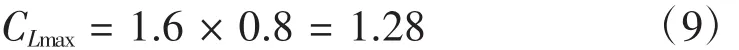
本文設計的輕型無人機應用于航測、實驗室飛控實驗等領域，且考慮到航線問題，一般飛行高度不超過300 m，則空氣密度ρ＝1.29 kg/m3由升力公式。

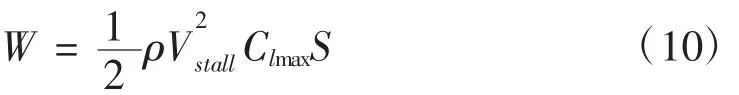
求出設計失速速度

（2）設計最大翼載

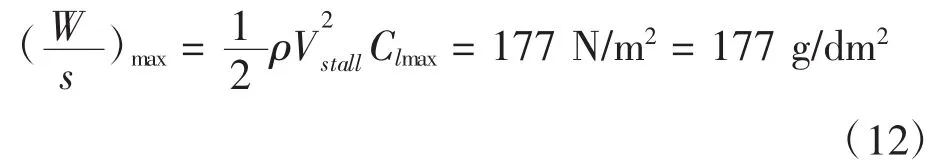
在輕型無人機設計中，為使飛機易于操控且不至于速度過大，翼載荷一般不超多200 g/dm2，故以上設計最大翼載荷符合要求。

2 無人機基本參數設計

2.1 機翼外形參數設計

對于輕型無人機而言，在設計機翼時，首先要把滿足設計要求的飛行技術性能作為主要依據，即應保證：

（1）在飛、著陸和空中機動狀態下有盡可能大的升力及高的升阻比；

（2）在巡航狀態和大速度下有盡可能小的氣動阻力；

本文設計的輕型無人機機翼相對機身的位置，采用中單翼，翼身干擾小，阻力小。為使飛機擁有更好的橫向穩定性以及更小的渦阻，將機翼形狀設計為類滑翔機狀態。得到：

等效展弦比λ＝14（第1章中已取定）

機翼展長l＝4 m（第1章中已取定）

機翼投影形狀設計為細長梯形狀，屬于平直機翼的變種，擁有較優良的氣動特性，生產加工方便，但是需要選擇好合適的根梢比。

由低速飛機根梢比取2.222…時有最小誘導阻力[5]，且經過驗證飛行可知，根梢比2.222…左右梯形機翼擁有最合理的載荷分布，故取根梢比

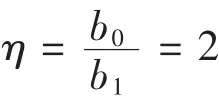
在前文已經取定平均氣動弦長b=0.281 m，則根據根梢比η=2可得：

翼根弦長

翼尖弦長

又根據翼展和平均氣動弦長已知，可求得

機翼面積

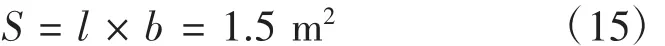
AH-79-100B翼型升力系數曲線和阻力系數曲線如圖4所示。

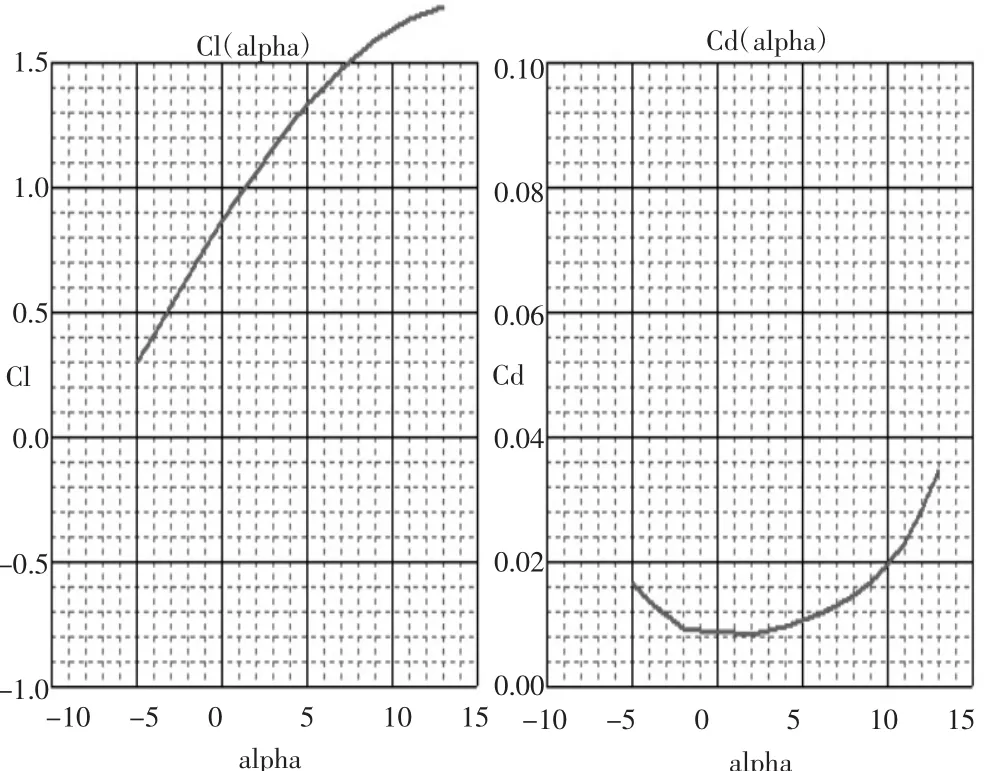
圖4 翼型升力系數、阻力系數曲線

本文設計的輕型無人機具有大載重量的特點，因此機身橫截面積會相對較大，綜合參考以上升力系數和阻力系數曲線，為了使飛機盡可能減小阻力的同時又兼具較高升力，所以取定：

機翼安裝角：

上反角可提供橫向安定效應；對于有后掠角的機翼，因側滑而產生橫向安定性[6]。而本文設計的輕型無人機采用了大展弦比中單翼設計，本身即具有很強的橫向穩定性。為防止橫向穩定過強，故機翼不設計上反角和后掠角。

由于設計采用的是根梢比為2的梯形機翼，綜合考慮氣流分量和后期制造難易程度，本文決定設計機翼前緣平直的直角梯形的機翼構型。

2.2 機身參數

2.2.1 機身長度

飛機起飛總重確定后，就可由表1中的數據得到機身長度的初值[1]。

表1 機身長度與起飛總重的關系

由設計最大起飛重量 ≤ 20 kg（即W0≤ 20 kg），查表得：A=1.6，C=0.23。

計算出機身設計長度

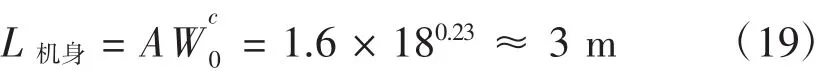
2.2.2 機身長細比

由已知定義，機身長細比＝機身長度／最大當量直徑，當機身內部體積一定，長細比為3.0左右亞音速機身阻力最小，長細比為14左右的超音速機身阻力最小，絕大多數的飛機機身的長細比在兩者之間[7]。

本文設計的輕型無人機屬于低空低速飛機，無考慮超大長細比，相反應該考慮以大容積大載荷量為設計目標。參考其他載運量較大的無人機最大截面直徑為0.23 m，擬定本文設計最大截面直徑為0.25 m。綜合參考之后，本文設計的輕型無人機擬設定機身長細比為4.0，即

則機身長度：

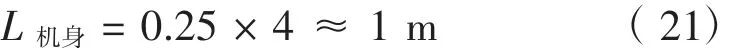
2.3 尾翼的布局及參數的選擇

本文設計的輕型無人機的尾翼的布置采用固定尾撐雙垂尾形式，并且把平尾抬高，避開了機翼尾流和螺旋槳滑流，使其效率提高，從而可以適當減小平尾尺寸，也為之后的飛控控制減少控制難度[8]。垂尾、平尾等翼面要在正負迎角、正負側滑角下工作，因此這些翼面都要采用對稱翼型[7]。

2.3.1 垂尾參數設計

飛機的航向安定性和操縱性是通過垂尾及方向舵來實現的[9]。為了達到更好的載荷分布效果，垂尾與主機翼一樣采用直角梯形外部形狀構型，方便生產制造。

尾翼的展弦比和尖削比參數如表2所示[1]。

表2 尾翼的展弦比和尖削比

上表中A為展弦比，λ尖削比（即為根梢比倒數）。

一般垂尾相對面積（SV/SW）大約為20%~25%，本文設計的輕型無人機將主要應用于航測、實驗室飛控實驗等領域，需要要求飛機具有較高的航向穩定性，所以設計取定：SV/SW=25%，則

由于本文設計的輕型無人機展弦比為14，與一般滑翔機類似，所以垂尾展弦比參考滑翔機范圍取值，兼顧尾撐式布局存在的扭轉風險，所以垂尾不設計太高，則取

本文設計的輕型無人機擬采用不小于23英寸（約0.6 m）的螺旋槳，為使平尾能夠有效脫離螺旋槳滑流的影響，則設計垂尾高度不小于0.45 m，兼顧考慮上文提到的不應有太高大的垂尾，則取定

較大的尖削比可是使平尾設計得更低矮但面積更大，同時小的尖削比可以提高翼面的失速角度范圍，使得垂尾工作在更廣闊的側滑角度里而不失速，且平尾高抬，類似T尾設計，所以參考數據，取

綜合以上數據，可計算出垂尾的基本設計值：

符合設計要求。

2.3.2 平尾參數設計

平尾的主要作用是平衡機翼產生的縱向力矩，它們所能提供的力矩效率與其產生的升力及力臂成正比，而升力與其面積成正比[9]。

由表2可知，一般平尾相對面積（SH/S）大約為20%~25%，因為本文設計將平尾高抬離開螺旋槳滑流區和機翼下洗區，且垂于兩垂尾之間，具有端板效應，所以平尾效率較高，可以適當采用較小面積的平尾設計。綜上所述，取定（SH/S）=20%

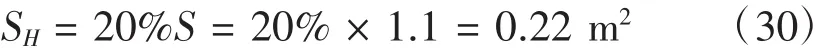
平尾設計采用矩形外觀構型，實用高效，便于安裝。

由于平尾設計安裝于平尾接近尖端處，所以將平尾安裝處設計在垂尾弦長0.25 m處，又因平尾為矩形構造，為不造成不必要的干擾阻力，故綜合考慮將平尾弦長設計定為0.25 m，即

根據已定的平尾面積SH=0.22 m2，計算出平尾展長lH≈0.9 m

則平尾展弦比AH=0.9/0.25=3.6，在可用范圍內。

2.3.3 尾容量設定及尾力臂確定

尾容量是衡量飛機尾翼對飛機俯仰、航向安定性的基本數值。尾力臂是指機翼平均氣動弦長前四分之一處到尾翼弦長前四分之一處的距離，相當于平垂尾為改變飛機姿態施力的力臂[10]。

如表3所示[1]，為經典飛機尾容量參考值。

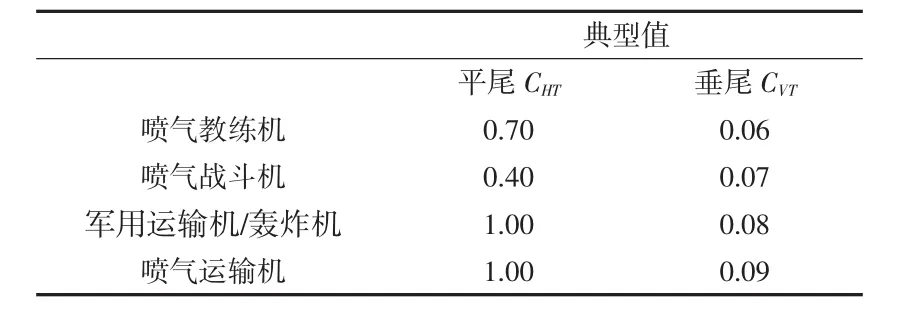
表3 平垂尾經典尾容量參考值

垂尾尾容量

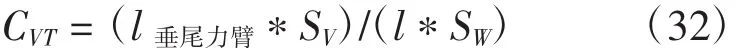
參考噴氣運輸機垂尾容量經典值，取CVT＝0.09

則：

平尾尾容量

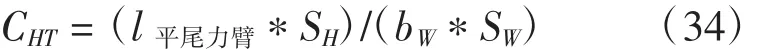
參考噴氣運輸機垂尾容量經典值，取CHT=1.00

則：

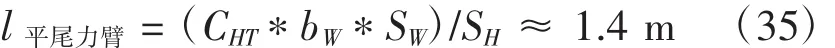
綜上，平尾力臂與垂尾力臂基本相等，則在具體設計當中只需注意將平尾和垂尾四分之一弦長點設計重合即可。

2.4 三維建模

利用航空工業中應用最廣的三維建模軟件CATIA，根據以上設計出的參數進行本文輕型無人機的三維建模工作。三視圖及等二軸測圖如圖5所示。

圖5 三維模型的各個視圖

3 總結與展望

本文設計確定了一種大載荷量無人機的基本參數，計算了基本飛行數據，建立了該輕型無人機的三維氣動外形模型。設計過程表明，該輕型無人機設計方案可行，為后續的研制工作做了較為充足的理論設計準備。該輕型無人機主要適用于飛控驗證飛行，也可適用于航空測繪、森林防火、國土資源調查等領域。