潛艇設備沖擊響應譜譜跌特性數值分析

王曉欣，李笑天 ，馬笑輝 ，杜國偉

1清華大學核能與新能源技術研究院，北京100084

2清華大學先進核能技術協同創新中心，北京100084

3清華大學先進反應堆工程與安全教育部重點實驗室，北京100084

4同方工業有限公司，北京100083

0 引 言

爆炸沖擊載荷作用是導致艦載設備失效的重要因素，分析和評估設備抗沖擊性能是設計中的重要環節［1］。基于沖擊響應譜的抗沖擊數值計算方法因計算量小、易使用，在艦載設備設計分析中得到了廣泛應用。設計沖擊譜是響應譜法抗沖擊分析中的輸入條件，決定了抗沖擊計算的準確性［2］。在20世紀60年代，研究者使用與地震工程中類似的包絡譜計算了艦載設備的沖擊載荷，其值足以造成艦艇結構發生破壞，但在實船測試中，設備卻保持完好。可見，計算與實驗結果差距甚大，由此促使研究者對艦艇沖擊響應譜進行了深入研究。O'Hara等［3-4］提出了譜跌概念，指出艦載設備與艦艇間的相互作用可以使設備固有頻率處的響應譜值降低約1個量級。基于該理論，Remmers等［5］提出了用于艦艇設計的DDAM（Dynamic Design Analysis Method）譜分析法，至今仍在艦載設備設計領域被廣泛使用。對于譜跌效應，國內外也都開展了相應的研究工作［6-8］。DDAM方法中給出了考慮譜跌效應的沖擊設計響應譜，且譜值與設備質量有關。我國現行的潛艇設備沖擊設計規范遵循國軍標 GJB 1060.1-91［9］，其設計響應譜參考了DDAM中的響應譜。

國內學者雖然對抗沖擊設計譜開展了研究［10-11］，但對響應譜公式的推導過程、參數來源及其適用范圍（例如，潛艇質量與形式、設備連接方式等）的理解尚不甚清晰，故有必要對潛艇譜跌效應產生的規律進行深入研究。本文將針對特定外形的潛艇，研究艇體與不同質量及頻率的設備在不同連接方式下兩者之間產生的相互作用，以得到考慮了譜跌效應的設計響應譜，并針對DDAM方法及國軍標響應譜的適用性開展討論。

1 計算模型

1.1 有限元模型

本文考慮了潛艇設備與艇體的相互作用，并針對典型的潛艇艙段結構進行了沖擊動力響應分析。圖1所示為研究“譜跌效應”采用的簡化質量彈簧結構，通過該結構模擬與艇體連接的設備及其支撐的影響，其中設備與艇體肋骨連接。圖中：M，K分別為設備質量及支撐剛度，A為設備與艇殼的連接點。

采用ABAQUS有限元分析軟件建立潛艇艙段的三維模型，并開展沖擊動力響應的數值計算。圖2（a）所示為潛艇艙段的有限元模型，圖2（b）為單自由度設備與艇體的連接方式。其中，艇體、肋骨分別采用殼單元和梁單元模擬；設備通過集中質量模擬，設備與艇體間通過在垂向具有自由度的彈簧連接；設備支撐位置處的艇體固有頻率約為102 Hz；沖擊加速度時程沿垂向（y）作用于艙段模型兩端。通過對模型進行時域內的動力響應計算，得到0.5 s內A點的加速度響應時程，并生成了沖擊響應譜。

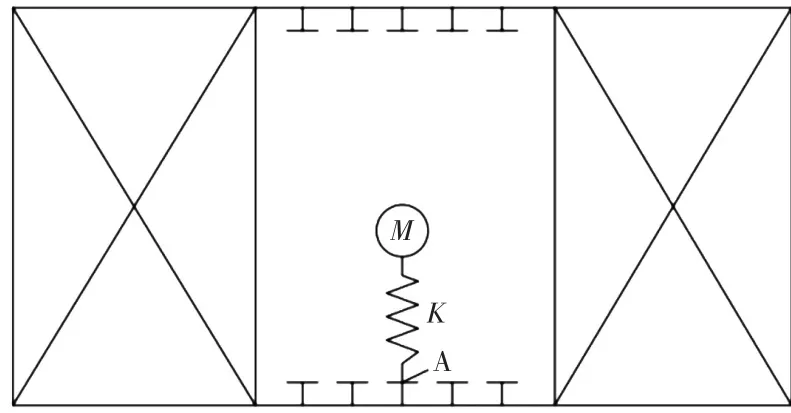
圖1 譜跌效應計算模型示意圖Fig.1 Illustration of numerical model for spectrum dip effect analysis

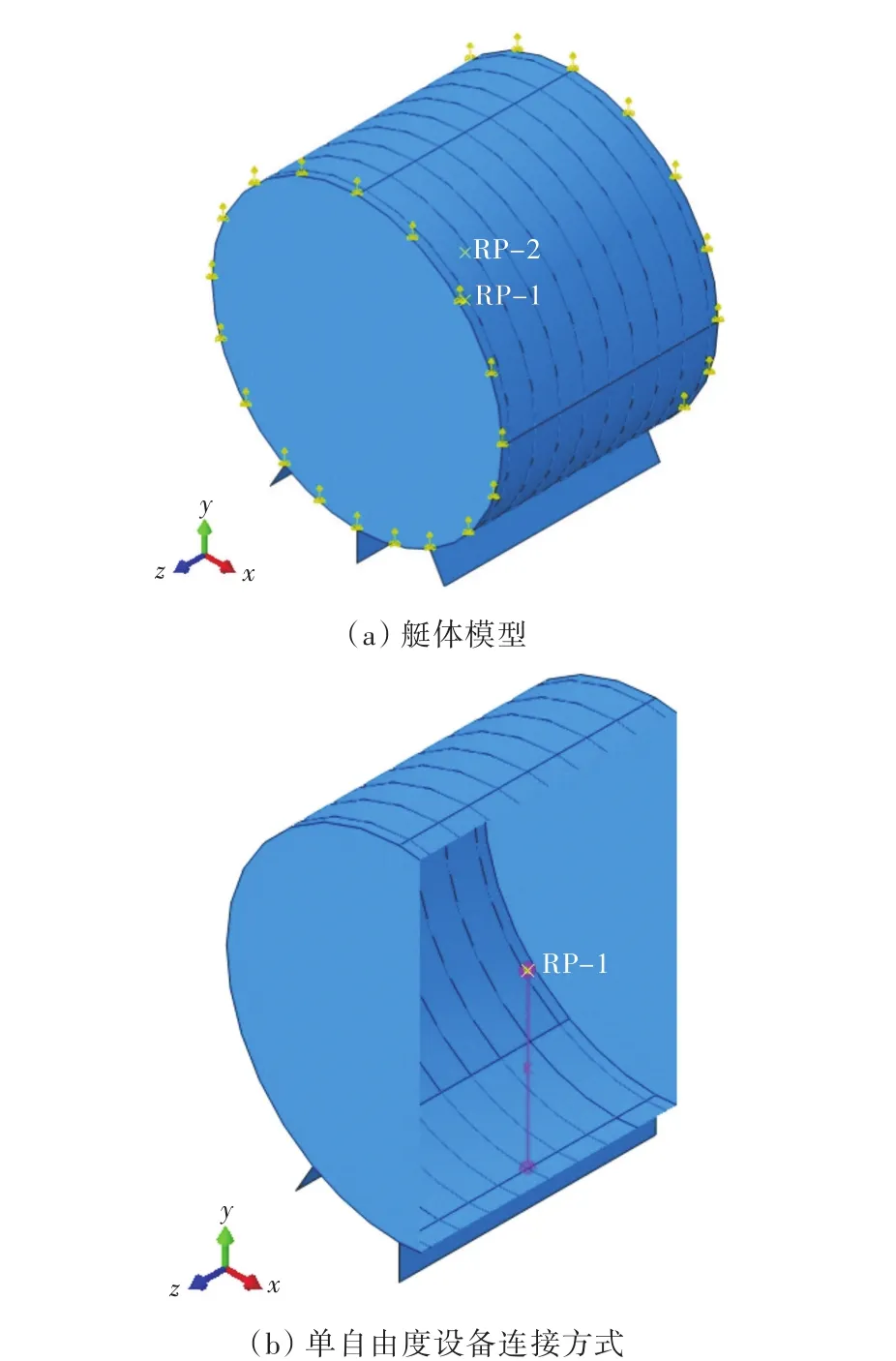
圖2 譜跌效應有限元計算模型Fig.2 Finite element model for spectrum dip effect analysis

1.2 沖擊輸入

潛艇艙段沖擊設計譜采用典型的三折線譜，其速度段和加速度段采用國軍標中的沖擊譜。其中，潛艇設備的沖擊加速度設計值A0與沖擊速度設計值V0分別由下式計算：

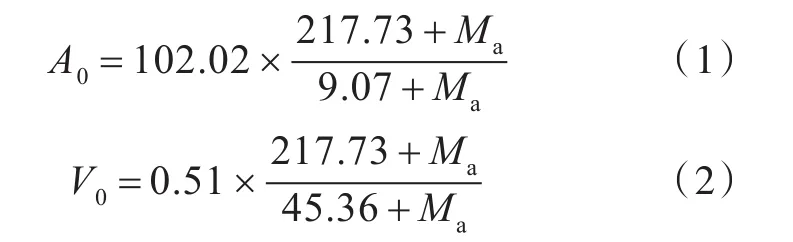
式中，Ma為艙段附加設備的模態有效參與質量。令Ma=0，則A0和V0為未考慮附加設備質量的沖擊設計值，以此作為艙段的沖擊設計值，即A0=2 450 m/s2，V0=2.45 m/s。艙段沖擊設計譜的位移段U0取為0.04 m。圖3（a）所示為艙段沖擊設計譜。

利用BV 043/85德國國防軍艦載設備設計規范［12］，得到與圖3（a）三折線譜相對應的正、負三角波加速度時程曲線如圖3（b）所示。

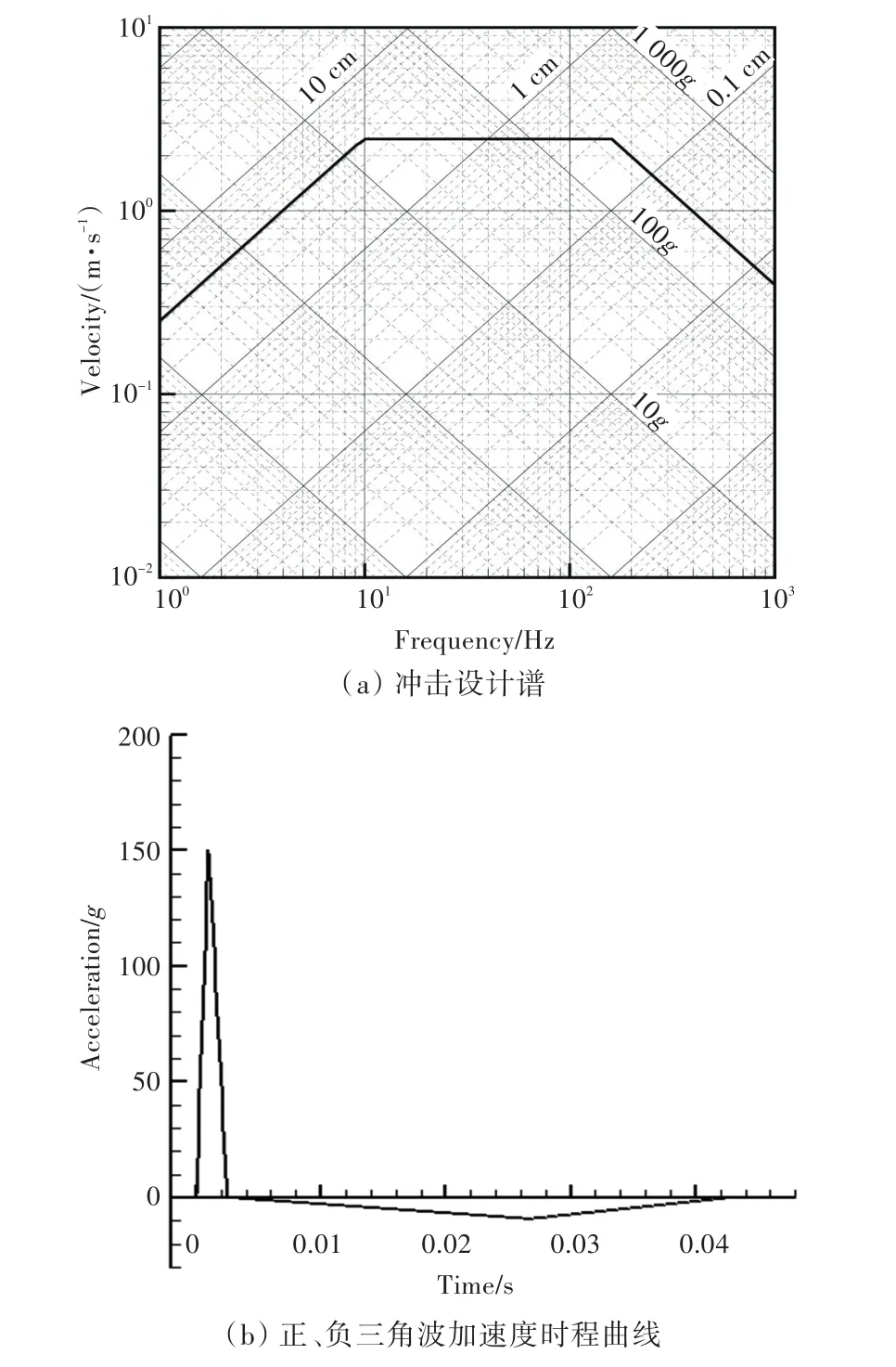
圖3 潛艇艙段沖擊響應分析輸入條件Fig.3 Inputs for shock response analysis of the submarine cabin

2 單自由度系統譜跌規律

2.1 設備質量、頻率對譜跌的影響規律

利用1.2節中的有限元模型，計算不同質量M及固有頻率fe的附加單自由度系統給潛艇艙段沖擊動力響應帶來的影響。對于單自由度系統，式（1）和式（2）中Ma=M，故將以下單自由度質量記為Ma。計算中，Ma分別取為1，5，10，50，100，150，200，250，300 t，通過調整彈簧剛度，使單自由度系統固有頻率fe分別達到 2.5，5，10，25，50，100，120，200，500，1 000 Hz。基于上述取值，模擬安裝在艇體上具有不同剛度的設備—支撐系統，共計有90種質量—頻率組合。單自由度系統與艇體艏、艉艙壁中點位置的一根肋骨相連。圖4所示為典型的設備固有頻率下設備與艙段連接時連接點A處的沖擊響應譜計算結果。

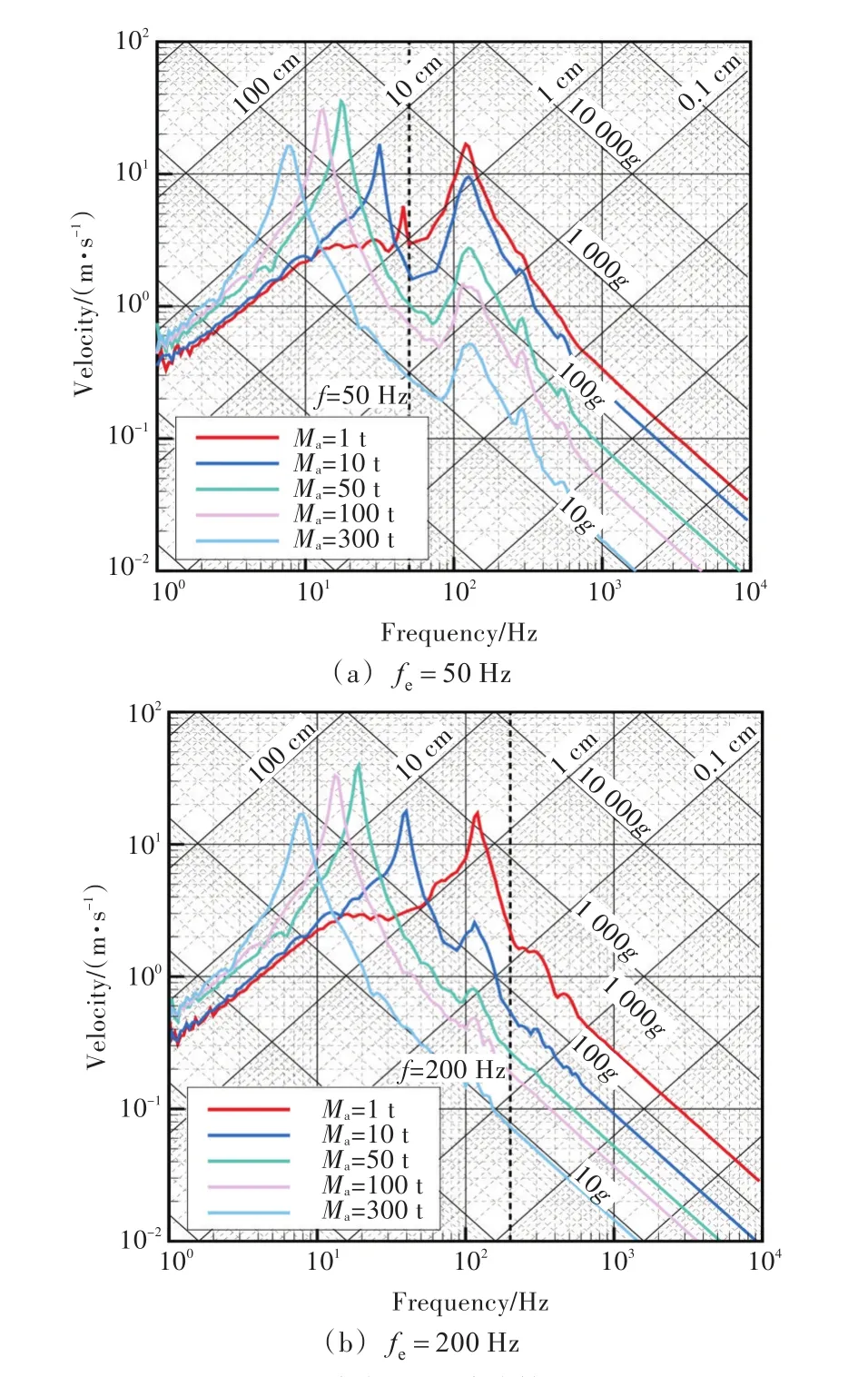
圖4 沖擊響應譜計算結果Fig.4 Calculation results of the shock response spectra

隨著設備質量的增加，在各種頻率范圍內，響應譜的計算結果與無設備時響應譜的差別增大，固有頻率fe處的響應譜譜值逐漸減小。該頻率處所對應的響應譜值正是采用響應譜方法分析設備應力時所使用的設計加速度值。因此，若忽略設備與潛艇艙段的相互作用而使用無設備時的響應譜，則加速度值會偏大，導致應力計算結果過于保守。這說明，在使用響應譜法分析潛艇設備的應力時，需考慮艇體與設備間相互作用的影響，即“譜跌效應”。潛艇在安裝了反應堆等大質量設備后，艇體與安裝設備間的相互作用將非常強烈，若計算時忽略譜跌效應，可能會得到與真實響應及應力水平完全不符的結果。

圖5所示為采用潛艇艙段與不同質量—頻率組合下連接設備時連接點A處的響應譜曲線在fe處的譜值。對于不同的設備質量，各頻率下計算得到的結果可以構成一條響應譜曲線。當Ma=1 t時，安裝設備對潛艇艙段的影響很小，響應譜曲線與不考慮設備影響的設計響應譜基本重合。隨著Ma的增加，對安裝設備的影響逐漸增大，響應譜在各頻率上的譜值均逐漸減小，譜跌效應顯著。

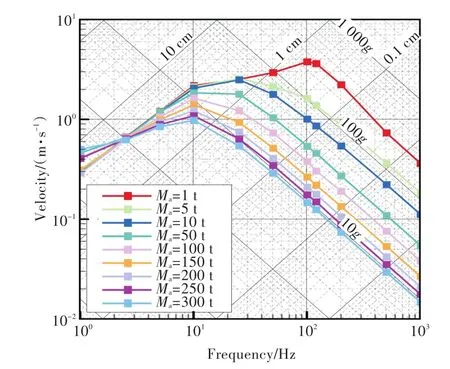
圖5 不同質量—頻率組合下設備沖擊譜值計算結果Fig.5 Calculation results of the shock spectrum value for equipment with different combinations of mass and frequency

由圖5可知，在考慮譜跌效應的響應譜中，低頻段為明顯的等位移段，在高頻段，加速度基本上不隨頻率發生變化，即為等加速度段。雖然兩者間為等速度段，但對應的區間相對較小。圖6(a)所示為等加速度段加速度譜值隨設備質量變化的情況。圖中：虛線為對數坐標下的加速度線性擬合曲線，A0=286.92Ma-0.575，線性擬合度 r2=0.992 8。除在設備質量較小（Ma＜2 t）的情況下，計算得到的加速度譜值均小于國軍標給出的譜值。當Ma=5～300 t時，國軍標給出的加速度譜值與擬合譜的加速度譜值的相對偏差為30%～40%。圖6（b）所示為等速度段的速度譜值隨設備質量變化的情況。圖中：虛線為對數坐標下的速度線性擬合曲線，V0=3.928 7Ma-0.219，線性擬合度 r2=0.959 3。對于各種質量的設備，計算得到的速度譜值均大于國軍標給出的速度譜值，最大相對偏差約60%。

根據分析結果，發現在等位移段譜跌效應的影響不明顯，設備質量不同的沖擊響應譜變化不大。因此，在等位移段，忽略譜跌效應的影響，將位移譜值U0保守地取為0.04 m。

綜上所述，針對本文研究的潛艇外形，在考慮譜跌效應的影響下，可得到設備沖擊加速度設計值A0、沖擊速度設計值V0及位移U0分別如下：A0=286.92Ma-0.575，V0=3.928 7Ma-0.219，U0=0.04 m。

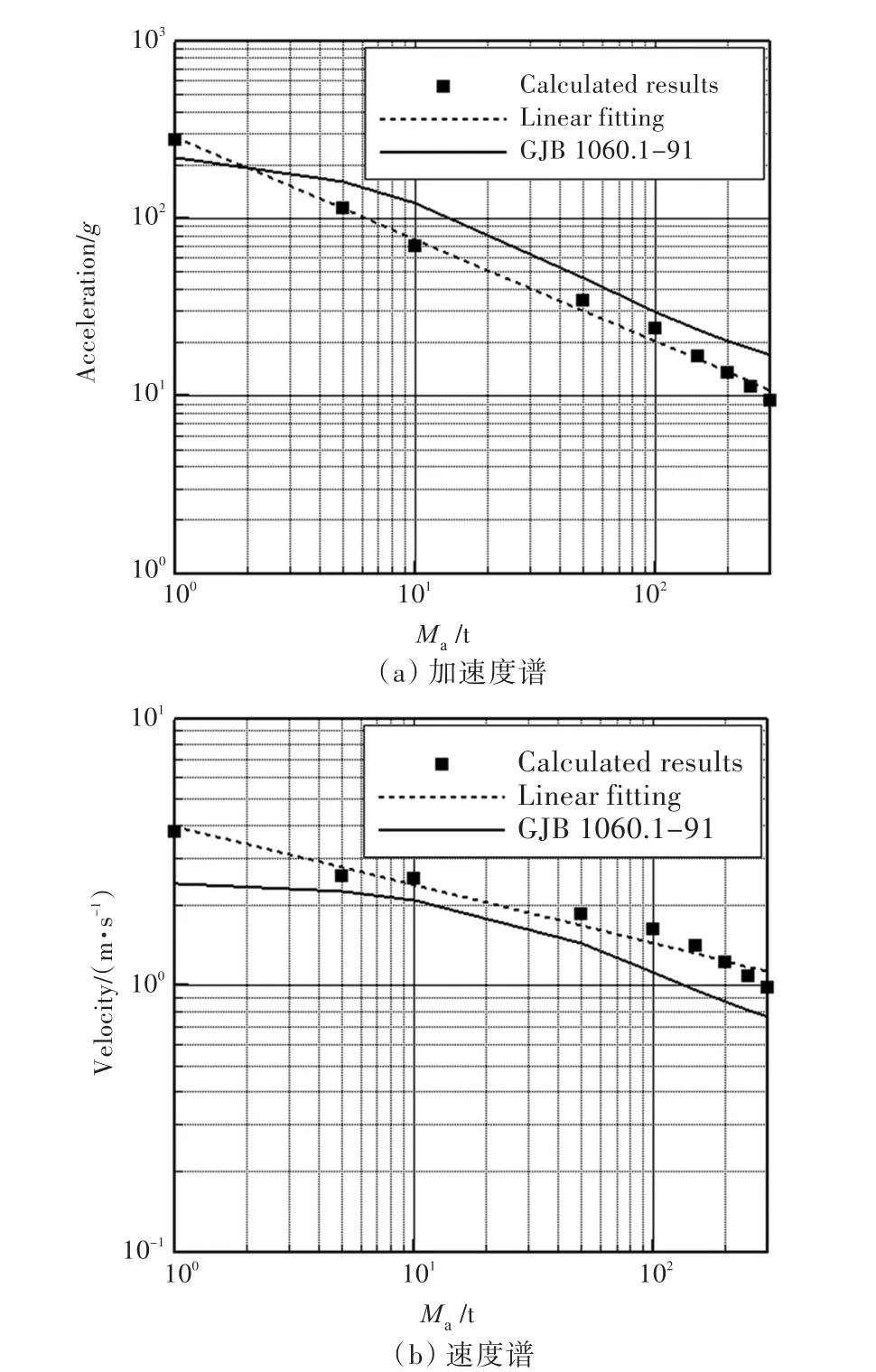
圖6 計算譜值隨設備質量變化Fig.6 Variation of the calculated spectrum values with equipment's mass

2.2 與國軍標沖擊設計譜的對比

圖7所示為Ma=5和50 t時本文計算得到的沖擊設計譜與國軍標給出的結果對比。

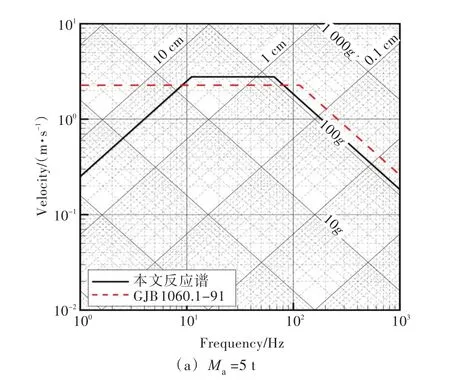
本文在計算沖擊設計譜時對于低頻段考慮了等位移段，而國軍標給出的沖擊設計譜在中、低頻段均采用了等速度假設，故本文在低頻段計算得到的響應譜小于國軍標給出的譜值。

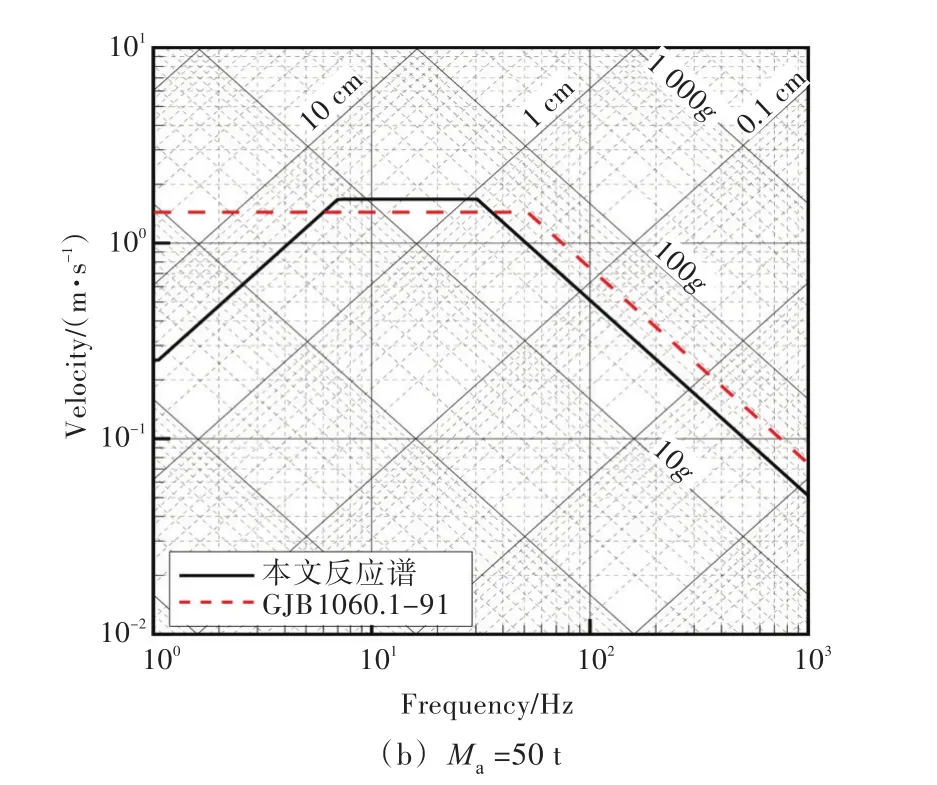
圖7 本文計算的沖擊設計譜與GJB 1060.1-91譜值對比Fig.7 Comparison between the current calculated spectrum values and the GJB 1060.1-91

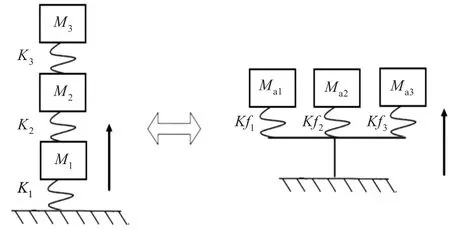
圖8 多自由度系統解耦示意圖Fig.8 Schematic diagram of decoupling of a multi-DOF system

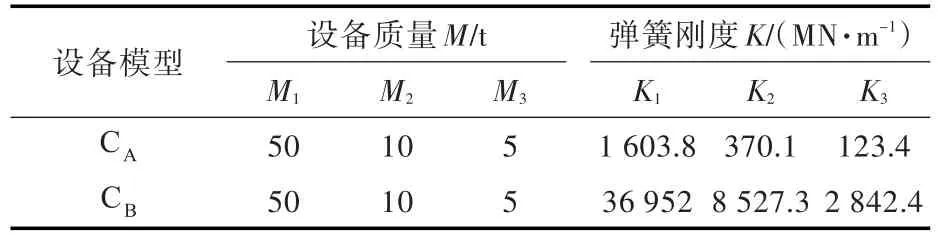
表1 多自由度模型質量與彈簧剛度Table 1 Mass and spring stiffness of the multi-DOF model

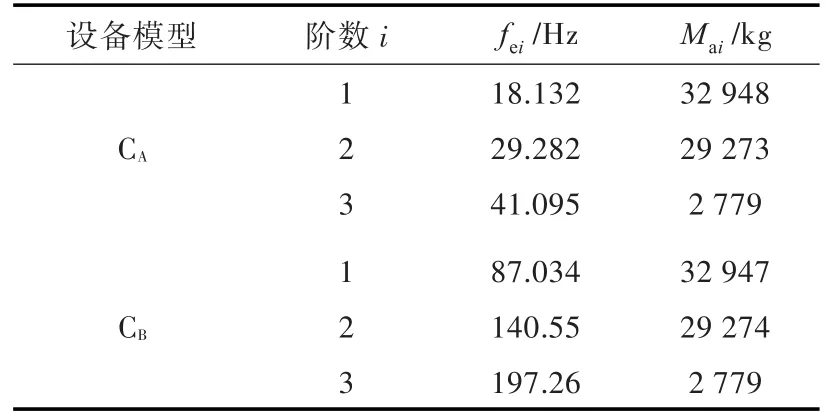
表2 多自由度模型各階固有頻率與模態有效參與質量Table 2 Natural frequencies and modal effective mass of the multi-DOF model

由于本文的響應譜在等加速度段小于國軍標給出的譜值，在等速度段大于國軍標的譜值，從響應譜譜型來看，本文給出的響應譜速度段較短，且隨著設備質量的增加，等速度段的區間進一步縮小。

根據以上分析，對于本文所研究的特定外形潛艇，國軍標給出的設計響應譜在高頻段偏大，在中頻段偏小。考慮到艦載設備及其支撐的頻率很可能處于中頻段，使用國軍標給出的設計響應譜進行設備響應分析不一定是完全保守的，故有必要針對特定外形的潛艇開展針對性分析。

3 多自由度系統譜跌規律

本節將單自由度的計算結果推廣至多自由度系統。根據模態分析理論，多自由度系統的運動方程解耦后，可轉化為相互獨立的若干單自由度系統的運動方程。圖8所示的右側為多自由度系統等效模型［5］。圖中，Mai為左側系統第i階模態的有效參與質量，Mai和Kfi構成的彈簧質量系統的固有頻率為左側系統的第i階固有頻率fei。兩種系統對于基礎的影響是等價的。本節考慮的兩種典型設備（中低頻設備CA，高頻設備CB）的質量與剛度特性由表1給出。表2給出了多自由度模型的各階固有頻率和模態有效參與質量，由此可以構造圖8中的等效單自由度系統。

根據DDAM方法［5］，多自由度系統考慮譜跌效應的響應譜值由各階模態所對應的固有頻率fei和模態有效參與質量Mai確定。該譜值可認為是各階模態所對應單自由度系統獨立作用于潛艇艙段時得到的響應譜譜值。當設備支撐在完全剛性的基礎上時，該方法得到的結果是精確的；但對于艦載設備，因其與艇體間的相互作用將導致艇體產生變形，若采用該方法計算，會產生一定的偏差。

圖9所示紅、綠、藍三色曲線分別為潛艇艙段單獨連接固有頻率為fei、質量為Mai(i=1,2,3)的單自由度系統得到的響應譜。圖中，曲線在fei處的響應譜值即為用于DDAM譜分析法計算的設計響應譜值，并以相應的彩色圓點標記，該譜值可由式（1）計算；黑色實線是對圖8左側多自由度系統直接進行時程響應計算并生成的連接點A處的響應譜，該曲線可以認為是多自由度系統響應譜方法所輸入的響應譜精確解。

由圖9中黑色與彩色圓點的對比可知，多自由度系統與等效單自由度系統的響應譜值相比存在一定的偏差，這兩個系統并不完全等價。這是因為在多自由度同時作用下的艇體變形與在單自由度單獨作用下的不同，設備的加速度響應也隨之不同。在此情況下，多自由度系統的各階模態間存在相互影響，無法簡單解耦。而目前的DDAM方法也未考慮艇體變形引起的多模態間相互作用對響應譜值的影響。

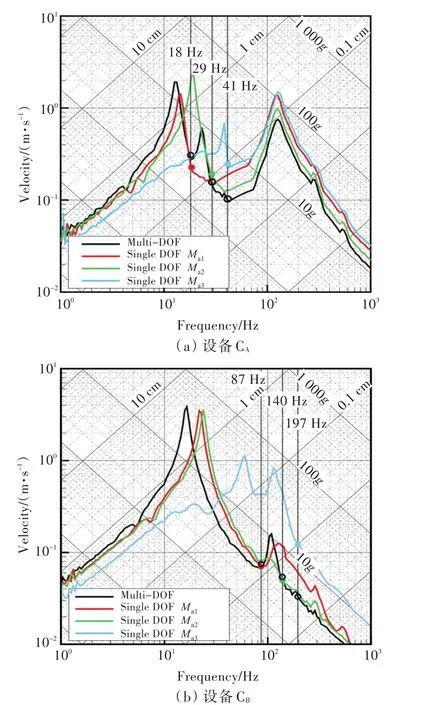
圖9 多自由度模型與等效單自由度模型響應譜計算結果對比Fig.9 Comparison between the calculation results of multi-DOF models and equivalent single DOF models

從圖9中低、高頻兩種頻段設備的計算結果來看，單自由度模型加速度響應可能存在偏大或偏小的情況，這均與設備的固有頻率及模態有效參與質量有關，影響規律較為復雜。由于低階模態參與質量較大，低階模態對高階模態的影響較大，高階模態譜值偏差也較大。在低階模態影響下，高頻處的譜跌效應更明顯，從而使響應譜值減小。由圖9可知，在高階模態處考慮模態間的相互作用與不考慮時相比，最大偏差約為5倍。而由于高階模態參與質量小，其對低階模態的影響相對也較小。在有效地將各階模態的計算結果組合后，可得到圖8左側系統各質點的加速度；與多自由度模型的計算結果相比，單自由度解耦模型的計算結果偏大，對于本節計算的兩種設備，最大偏差約為2倍。

根據以上結果，使用DDAM方法因忽略了模態間的相互作用，造成與真實響應譜存在一定的偏差，導致動力響應分析結果偏于保守。在某些情況下，DDAM方法的偏差較大，計算過于保守。為了得到更精確的計算結果，此時有必要針對艙段和設備建立整體模型，以獲得設備支撐位置處的真實響應譜，并用于后續計算。

4 設備與艙段連接方式影響

上文在研究單自由度和多自由度系統與艙段的相互作用時，將設備與艇體的連接方式簡化為了單點連接。而在實際情況下，設備支撐與艇體存在不同的連接方式。例如，反應堆之類的大型設備與艙段就存在較大的連接面積，此類連接方式勢必對艙段的動力響應造成一定影響。本節通過4個模型（Model 1～Model 4）來考慮設備與艇體的不同連接面積對沖擊響應譜的影響。這些模型中的設備均為雙自由度系統，其中設備質量及其固有頻率分別為：Ma1=50 t，fe1=30 Hz；Ma2=15 t，fe2=50 Hz。模型1中的設備與艇體間采取點連接方式，模型2～模型4中的設備采用裙式支撐。與艇體的連接半徑R分別為0.5，1.0，1.5 m。

圖10所示為4種模型在不同連接方式下設備支撐位置的響應譜計算結果。由圖可知：隨著設備與艇體連接半徑的增大，連接處的剛度有所增強，艇體與設備構成系統的一階頻率（響應譜曲線第1個峰值對應的頻率）有所增加；響應譜曲線在設備固有頻率fe1=30 Hz及fe2=50 Hz處的取值即為設備的沖擊加速度設計值；隨著設備與艇體連接半徑的增加，上述設備頻率處的響應譜值均有所增大，當連接半徑從0.5 m增大到1.5 m后，加速度響應譜值增加為原來的1.5倍，這是因為在艇體與設備連接處的剛度增加后，設備質量對艇體造成的影響減弱，譜跌效應隨之減弱。

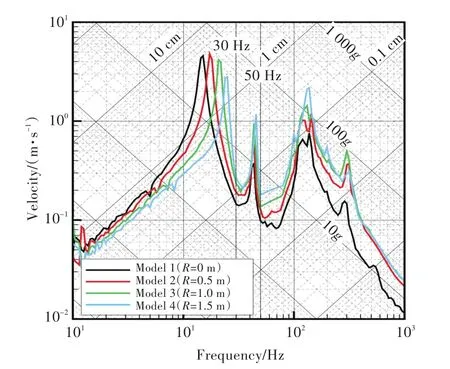
圖10 不同連接方式下模型響應譜計算結果Fig.10 Calculation results of the models with different connections

根據以上分析結果，設備與艇體的連接方式對設計響應譜存在顯著影響。DDAM方法的設計譜不能涵蓋各種支撐方式、連接面積的影響。對連接面積較大的大型設備，為了獲得準確、可靠的動力響應計算結果，有必要建立艙段—設備耦合模型，以充分考慮設備支撐與艇體的相互作用。

5 結 論

本文研究分析了安裝大質量設備后的潛艇動力響應特性，建立了簡化的艙段—設備有限元模型，通過數值計算，研究分析了不同因素對譜跌特性的影響規律，得到如下結論：

1）對于艇體與單自由度設備模型，在低頻段（位移段）和高頻段（加速度段），國軍標給出的沖擊譜更保守；在中頻段（速度段），國軍標給出的響應譜偏小。

2）對于艇體與多自由度設備模型，目前使用的響應譜方法忽略了模態間的相互作用，與真實的多自由度系統譜跌特性存在一定的偏差；大部分情況下，國軍標的處理方法偏保守，可滿足工程要求。但在某些特殊情況下，忽略模態間的相互作用將使設備設計得過于保守，付出的代價過大。

3）對于設備支撐形式對響應譜的影響，在不同連接方式下，設備與艇體間的相互作用會發生變化，艇體在支撐處的局部剛度也會隨之改變；連接半徑對設備的響應譜也存在明顯影響；隨著連接面積的增加，譜跌效應有所減弱。

綜上所述，設備響應譜受到多種因素的影響。在工程設計中，對于不同外形的潛艇，為了獲得可靠的沖擊響應，有必要在沖擊設計響應譜的選取方面開展針對性分析。鑒于DDAM方法及其設計響應譜的局限性，對于精度要求較高的大型設備，在進行動力響應分析時，有必要對艇體與設備的總體模型進行耦合分析，以充分考慮艇體與設備間的相互作用。

本文研究所建立的簡化有限元模型僅是艙段模型，且沖擊載荷采取了加速度形式的輸入，這與全艇在水下爆炸沖擊載荷作用下的真實響應可能存在一定的差異。

下一步，將針對潛艇—設備模型在水下爆炸沖擊載荷作用下的流固耦合進行精確計算，以更準確地模擬潛艇在安裝大質量設備后與艇體間的耦合作用，并在此基礎上對譜跌特性的影響規律和作用機理開展進一步研究。