共享經濟預約模式下資源分配的拍賣機制設計*

張 靜，張驥先，李偉東，劉旭東，張學杰+

1.云南大學 信息學院，昆明 650500

2.云南大學 數學與統計學院，昆明 650500

1 引言

共享經濟通過互聯網平臺將閑置的資源共享給他人，并從中獲取一定的金錢回報；對于用戶而言，無需購買資源，按需付費租賃即可，是一種新型的經濟模式[1-2]。共享經濟給人們生活方式帶來巨大改變，目前已遍及交通、住宿、餐飲、教育、醫療等領域。其運營模式主要分為預約模式和實時模式。預約模式中，用戶事先提出資源需求，待搜集所有用戶需求后，由提供商進行資源的租賃分配，用戶可在預約時間準時得到服務，如神州專車的預約用車服務。實時模式下用戶實時提交需求，系統立即從當前空閑資源中選取最合適的分給用戶，如滴滴打車。本文主要研究的是共享經濟預約模式下的資源分配與用戶定價問題。

在共享經濟預約模式中，如何將資源分時租賃給用戶使得提供商的收益最大化，是主要研究的問題。但目前的預約模式中，都是采用固定價格及先預約先服務的方式來分配資源，這種方式簡潔高效，但隨著市場的擴大，存在以下弊端。（1）固定的價格導致提供商收益低下。資源按使用時長收費，雖然會在高峰期調整倍數，但仍沒考慮市場實時供需情況，造成資源緊缺時不能提高價格，空閑時沒能降價使得資源閑置，收益較低。（2）資源分配不均導致資源利用率低。當用戶申請類型與閑置資源類型不符時，導致某些型號資源供不應求，其余卻大量閑置。（3）分配產生的碎片時間造成了資源浪費。先預約先服務的方式下，由于用戶的使用時間不確定性，產生很多碎片化時間浪費了資源。

拍賣機制是指通過相應的規則和買者競價來進行資源配置的一種市場機制[3]。將拍賣與共享經濟預約服務相結合，通過競價方式對資源進行全局規劃，能實現資源的合理配置；另一方面，拍賣根據相應的規則和市場供需情況動態決定用戶支付價格，保證公平性的同時吸引更多的用戶參加。

綜上，將拍賣應用于共享經濟預約模式中，可以解決當前市場分配方式存在的不足。基于此，本文提出一種公平可信的拍賣機制，用于解決共享經濟預約模式中資源的分配及用戶支付定價問題。該機制適用于按時收費的共享資源在預約模式下做分配，如共享停車位、共享住宿等；也適用于其他按時收費的資源，如云資源分配、醫療診治預約等。但共享經濟市場中還有一些移動的共享資源，其收費與取還點相關，如共享充電寶，這種復雜的情況不在本文考慮范圍內。本文貢獻如下：

（1）共享經濟預約模式的拍賣機制設計：基于共享經濟預約模式的特征，抽取出資源表示元數據，構建限制條件下以收益最大化為目標的整數規劃模型，同時在機制可信（strategy-proof）的基礎上，設計相應的資源分配算法及價格支付算法。

（2）資源分配算法設計：針對共享資源按時間段租賃的特性，設計最優資源分配算法；但最優資源分配算法具有較高的計算復雜度，因此結合關鍵路徑思想，設計單調的啟發式資源分配算法，能夠在接近最優解的前提下，提高計算效率。

（3）支付價格算法設計：最優機制中，設計基于VCG（Vickrey-Clark-Groves）理論的最優用戶定價算法；該算法同樣存在計算效率問題，近似機制中提出基于二分法的價格支付求解算法，能夠保證在機制可信的必要條件下，提高計算效率。

（4）對提出的拍賣機制進行了嚴格的理論證明，證明提出的最優和近似機制都是可信的。

本文組織結構如下：第2章介紹相關工作；第3章對共享經濟預約模式問題建模；第4章提出最優機制，包括資源的最優分配算法及基于VCG的支付算法；第5章提出啟發式機制，用關鍵路徑思想求資源分配，以及二分法求支付價格；第6章設計實驗來對比分析各算法；第7章總結全文并提出未來研究方向。

2 相關工作

目前，拍賣機制和共享經濟相關問題都已被廣泛研究，但將拍賣與共享經濟結合起來的研究還較少，相關工作主要分為以下三方面。

第一，共享經濟。目前對共享經濟的研究較少，大多從經濟學理論分析其商業模式及本質等；另一部分是針對共享經濟最重要的領域網約車的研究，包括乘客預測、訂單匹配、車輛實時調度等，并沒有涉及預約模式下資源配置問題。文獻[4]利用乘客運動模式及車輛GPS軌跡等來進行乘客預測；文獻[5]對用戶歷史數據建立貝葉斯框架，來預測用戶目的地分布，解決出租車與訂單更有效匹配的問題；文獻[6]開發基于PCA-WNN（principal components analysis wavelet neural network）的適應性機制進行出租車實時調度，但不適用于預約模式。

云資源也是一種動態共享的資源，云提供商已引入拍賣機制用于對云資源進行分配[7-8]；張林等人提出了一個在真實頻譜利用率及社會福利間取得權衡的可信拍賣機制，用于對頻譜資源拍賣[9]。根據拍賣在其他領域的應用，嘗試將拍賣與共享經濟結合，通過拍賣提高資源利用率，增加收益。

第二，資源分配。資源分配是實現拍賣機制的必要條件[10]。文獻[11]提出了PTAS（polynomial time approximation scheme）強近似機制，用于解決多資源的自主VM（virtual machine）配置問題。文獻[12]將Saas提供問題模擬為Stackelberg博弈，轉化為求解優化問題來求得分配策略。文獻[13]為基于拍賣的動態VM配置問題設計了真實的最優和近似機制。有的工作以綠色云計算為出發點，盡量最小化能源消耗[14]。文獻[15]的頻譜分配將空間上無沖突的用戶分組，對分組團體出價排序并分配資源。用戶分組給予本文啟發，與文獻[15]不同的是，本文按照資源成本降序并對用戶分組。文獻[16]提出真實的雙向頻譜拍賣機制，提高頻譜利用率。以往拍賣機制的目標大都為社會福利最大化，本文的研究中不同型號資源成本不同，目標為最大化供應商利潤。

第三，支付價格。分配完成后，需要合適的價格支付算法保證機制可信。廣義第二價格（generalized second pricing，GSP）思想簡單，被廣泛用于廣告關鍵字拍賣[17]，但GSP不可信，買方會謊報出價來獲益。部分研究中基于VCG理論求支付價格[13-14]，本文將VCG用于最優分配中保證可信。Mashayekhy等人提出的近似機制中用二分法求支付，能無限逼近最低獲得分配的價格[11]。普通二分法判定條件為用戶能否以新價格獲得分配，但共享經濟中新價格可能讓用戶分得低成本資源，不夠支付已租到的高成本資源，需對二分法進行改進。

以往的研究已經在共享經濟、拍賣機制、資源分配、支付價格方面取得了顯著的成果，其拍賣應用中用戶申請資源只會有分配和不分配兩種結果，目標為社會福利最大化；但在共享經濟中，用戶有多種型號可選擇，滿足成本價的情況下可以選擇高、中、低成本資源，對應的目標也需改為利潤最大化；而支付算法需保證用戶的支付價格大于所租資源型號的成本價。因此共享經濟中資源的分配及用戶定價問題與以往的拍賣應用大為不同，本文旨在設計針對共享資源的拍賣機制。

3 問題描述及模型定義

在共享經濟的預約模式中，供應商有多種型號的資源，并對應不同的成本價；用戶提交預約信息，包括使用時間段及競價，型號則由系統根據該時段競爭情況及用戶競價決定，以最大化資源利用率。供應商收集所有用戶的預約信息后，做出最合理的租賃分配方案以獲取最大收益。通過分析共享經濟預約模式的特征，對資源及用戶預約信息作簡一化處理，得到資源表示元數據，并根據共享經濟預約模式需滿足的約束條件，抽象出整數規劃模型。

資源信息定義：假設供應商有m個資源，資源集合為C={1,2,…,m}，對于每一個資源i∈C，對應一個單位時間使用成本價格ei，資源按照成本ei降序排序。目前供應商的資源一般有多種型號（如高、中、低檔次的汽車），每種型號有多個資源，每種型號的單價也不同。

用戶預約信息定義：假設有n個用戶的預約請求，用戶按照開始使用時間升序排序，用戶集合為U={1,2,…,n}，對于每個用戶j∈U，用戶的預約信息為qj=(sj,dj,bj)。其中sj為開始使用時間，dj為結束使用時間，bj為競價。

整數規劃模型：資源按照時間段租賃給各用戶，分配方案用矩陣X[m][n]表示，其中任意一個元素xij表示的是第i個資源租給第j個用戶的狀態。當xij=1時，表示i資源分配給第j個用戶，使用時間段(sj,dj)。當xij=0時，表示i資源不分給j用戶。本文所有矩陣的下標從1開始編號。

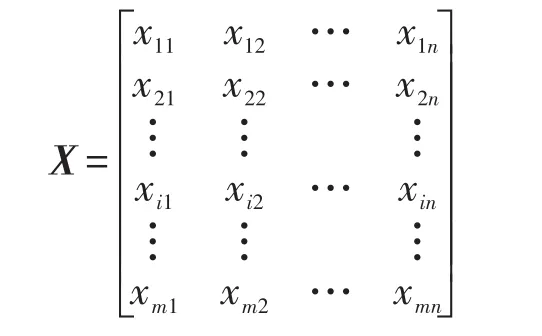
目標函數：

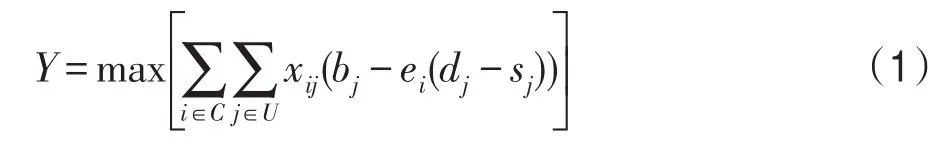
約束函數：

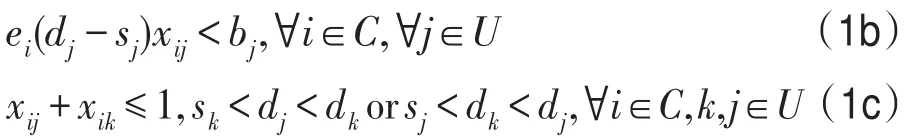
以往研究中目標函數都是社會福利最大化，即勝出拍賣用戶競價之和最大。但在共享經濟預約模式中，用戶可選擇滿足成本的多種型號的資源，但不同型號下競價是相同的，社會福利最大無法保證給用戶分配到最合適的資源，且易選擇使用時間長但利潤少的用戶。因此目標函數改為利潤最大化，才能保證供應商獲得最大的收益。最優租賃方案就在滿足上述3個約束條件下，使得目標函數最大的分配矩陣X。各約束條件的含義如下：

約束條件（1a）：對于每個用戶j，最多只會租到一個資源。約束條件（1b）：j用戶的競價必須大于i資源為其服務的成本，j才有可能租到i資源。約束條件（1c）：在求資源i的租賃分配時，對于任意用戶對(j,k)，若j用戶和k用戶的使用時間段有交集，i最多只能租給一個用戶，即xij+xik≤1。

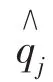
定義1（可信Truthfulness）一個可信的機制必須滿足：

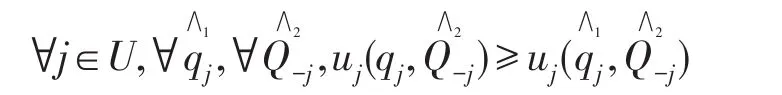
即當誠實報價是所有用戶的占優策略時，該機制可信[11]。

注：為了區別策略符號∧，標記j用戶采取策略為∧1，其他用戶集采取策略集合為∧2。

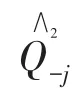
定義2（單調性monotonicity）當用戶j∈U在提交競價bj的情況下參與拍賣，租賃到i資源，若用戶j提高競價為bj′＞bj，則用戶j能租賃到與i同成本或者更高成本的資源，則稱該資源分配是單調的[11,13]。

定義3（臨界值critical value）用戶j∈U在提交競價bj的情況下租到i資源，對于用戶j存在一個臨界值cvj，當用戶改變競價為bj″，若bj″＞cvj時，用戶j才有可能租賃到與i同成本或更高成本的資源，反之一定不滿足[11,13]。

引理1一個拍賣機制M={A,P}，當其分配算法A求出的是最優解，支付算法P使用VCG計算，則機制M被證明是可信的[19]。

引理2一個拍賣機制M={A,P}，當其分配算法A滿足單調性，支付算法P是基于臨界值求解的，則機制M是可信的[18,20]。

4 資源分配和用戶定價最優機制

一個拍賣機制，包含資源分配算法完成對資源的優化配置，還要有支付算法計算拍賣勝出用戶需要支付的價格。資源分配和用戶定價最優拍賣機制包含以下兩部分：

（1）最優資源分配算法：得到資源的最優分時租賃分配方案，使得供應商獲得最大的利益。

（2）最優用戶定價算法：在最優租賃分配方案下，計算每個租到資源的用戶需支付的合理價格，以保證機制可信。

4.1 最優資源分配算法

最優資源分配算法，就是要求出資源的最優分時租賃分配方案，該方案下資源最大化利用，供應商利益最大化。根據整數規劃模型，用CPLEX求解器編程建立各個約束條件及目標函數。求出資源的最優租賃分配方案，得到拍賣勝出的用戶，以及給各用戶分配的資源，將各資源按時間段租賃給用戶，得到供應商的最大收益。

4.2 最優用戶定價算法

在求得資源的最優租賃分配方案的前提下，每個租到資源的用戶需支付給供應商相應的費用。VCG理論下，用戶的支付價格與自己出價無關，而是由市場決定，激勵用戶真實報價，保證機制可信。VCG對應的目標函數是社會福利最大化，即勝利用戶競價之和最大化；但在共享經濟資源配置中，不同型號資源的成本不同，競價最大不能保證利潤最大，因此目標為供應商利潤最大化。而相應的價格算法也需對VCG基礎算法進行改進。

沒有勝出拍賣的用戶支付價格為0，勝出的用戶j需要支付的價格為pj，假設j用戶租到i資源，又設用戶j應該付給供應商的利潤為fj，則：

式（2）表示用戶j給供應商支付的價格pj為兩部分相加，fj是j給供應商的支付利潤，ei(dj-sj)是i資源為j提供服務的成本。

基于VCG理論求解支付價格，用戶需要支付的費用為他參與拍賣給別的用戶帶來的損失之和，即用戶不參與時的社會福利，減去用戶參與時的福利剔除用戶競價[21]。但最優分配中，目標函數為供應商最大化的利潤和，對等的，在求解用戶j的支付利潤fj時應用VCG算法。用戶j的預約申請為qj，所有用戶的預約請求集合為Q，除去j剩余用戶的請求集為Q-j。對所有用戶調用最優分配算法為A(Q)，對除去j的用戶集調用最優分配算法為A(Q-j)。即支付利潤fj計算公式如下：

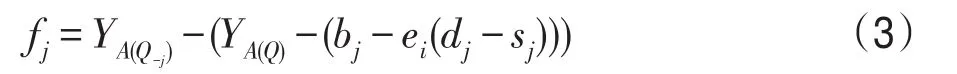
式（3）嚴格按照VCG理論計算，每個勝出的用戶需要支付的利潤值fj為他參與拍賣給別的用戶帶來的利潤損失之和。即fj為兩部分相減，YA(Q-j)為j用戶不參與拍賣下供應商的利潤和；(YA(Q)-(bj-ei(dj-sj)))為用戶j參與拍賣時供應商的利潤和YA(Q)減去j用戶租賃i資源所貢獻的利潤(bj-ei(dj-sj))。

將式（3）帶入式（2）得：

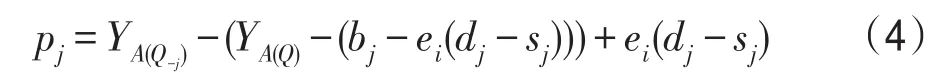
化簡式（4）得到：

即pj為兩部分相減，YA(Q-j)是j不參與拍賣下的利潤和，(YA(Q)-bj)是j參與拍賣下的利潤和剔除j的競價bj。

定理1最優拍賣機制是可信的。

證明最優拍賣機制的最優分配算法中，按照整數規劃模型用CPLEX編程求解，遍歷了所有分配方案的可能性，找出其中讓利潤最大的方案，即得到資源分配的最優解；最優用戶定價算法是基于VCG計算的。基于引理1，求出最優資源分配方案，并基于VCG理論計算支付價格的拍賣機制是可信的[19]。因此最優拍賣機制是可信的。

5 資源分配和用戶定價近似機制RAUPAM

雖然最優機制能求得最優的租賃分配方案，使得供應商的利益最大，但其時間復雜度很高，當用戶數目增多時，求解時間呈指數級別增長。因此提出了一種共享經濟預約模式下資源分配和用戶定價的近似機制RAUPAM（resources allocation and user payment approximation mechanism）。

近似機制包括以下兩部分：

（1）資源分配近似算法RAAM（resources allocation approximation mechanism）：根據共享資源分時租賃的數學模型，在滿足各個約束條件下，設計單調的啟發式資源分配算法，能夠在接近最優解的前提下，提高計算效率。

（2）用戶定價近似算法UPAM（user payment approximation mechanism）：在求得近似的租賃分配方案后，在保證機制可信的前提下，計算出每個租到資源的用戶需要支付的價格。

5.1 資源分配近似算法RAAM

啟發式的資源分配近似算法RAAM將資源分時租賃問題轉化為資源的時間分配圖，將每個資源可租賃的用戶按照時間先后鏈接在圖上，復雜的資源調度問題轉化為圖問題，進而用關鍵路徑思想得到資源最大近似分配。設計算法并滿足模型中的三個約束條件：用戶只能租到一個資源、租賃需滿足成本價、有時間交集的用戶不能同時租到同一資源。RAAM的偽代碼如算法1所示。

算法1RAAM求解資源分配方案

輸入：資源總數m，各資源的單位時間成本ei；用戶總數n，所有用戶的預約集Q，其中qj=(sj,dj,bj)。

輸出：資源租賃分配矩陣X[m][n]，供應商收益Y。

預處理：

1.ei降序排序，給對應資源編號，得到資源集合C={1,2,…,m}，成本集合E={e1,e2,…,em}。

2.Q按照qj中的sj升序排序，得到用戶集U={1,2,…,n}與預約信息集Q={q1,q2,…,qn}。

3.X[m][n]初始化所有元素為0，供應商利益Y=0。

4.系統用戶集初始U={1,2,…,n}，當前資源用戶集U′。

程序：

1.for eachi∈Cdo

2.U′=U

3.for eachp∈U′do

4.Ifei(dp-sp)≥bpthen

5.U′p/*剔除競價≤成本的用戶*/

6.end if

7.end for

8.R[n+2][n+2]={0}/*初始化所有元素賦0*/

9.for eachj∈U′do

10.R[0][j]=bj-(dj-sj)ei

11.end for

12.for eachj∈U′do

13.for eachk＞jandk∈U′do

14.ifdj≤skthen /*j和k無時間交集*/

15.R[j][k]=bk-(dk-sk)ei=R[0][k]

16.end if

17.end for

18.end for

19.R[n+2][n+2]調用關鍵路徑算法，求得0到(n+1)的關鍵路徑長度賦值給yi

20.Y=Y+yi

21.for each 關鍵路徑除0和(n+1)外涉及的節點jdo

22.xij=1

23.U j/*從系統可用用戶中刪除j*/

24.end for

25.end for

26.returnY,X[m][n]

RAAM算法將資源按成本降序排序，優先分配成本高的資源，其淘汰的用戶還能繼續租到低成本資源，最大化資源利用率；且給用戶優先分配高成本型號，提高了用戶滿意度。U存放系統當前可用用戶，更新篩選掉已租到資源的用戶，滿足一個用戶只能租到一個資源。按順序取一個資源i作為當前資源，其用戶集U′=U，并刪除競價低于成本的用戶，U′存放當前資源的可用用戶，滿足競價高于成本才能租賃。資源i對U′調用構建路徑-關鍵路徑算法，求出i的租賃方案及收益。

構建資源i的關鍵路徑時，根據其單價及可用用戶的預約信息，構建矩陣R[n+2][n+2]，R中0代表源節點，(n+1)代表終節點，其余n個節點為n個用戶。源節點0到U′中各用戶節點j的路徑等于資源i為j服務的利潤；j到終節點的路徑為0。因為U′中用戶按照開始使用時間排序，對于U′中所有用戶對(j,k)，當j的結束時間早于k的開始時間，j到k有路徑相連，長度為i租給k獲得的利潤，滿足沒有時間交集的用戶才有可能租到同一個資源的約束條件。通過上面步驟，將資源i能服務的用戶按時間先后聯通在一個圖上。對R調用關鍵路徑算法，求得0到(n+1)節點的關鍵路徑長度，即i租給U′中用戶所能獲得的最大利益，所有資源的利益相加就是供應商獲得的總利益。i的關鍵路徑中除0和(n+1)外涉及的節點j，成功租到資源i，在分配矩陣中標注xij=1，并從U中刪除，將不會租到別的資源。

完成i資源的構建路徑-關鍵路徑算法后，取下一個成本較低的資源繼續前面的步驟。直到所有資源分配完后，得到供應商的資源分配方案X[m][n]及獲得的總利潤Y。

定理2RAAM求的分配方案是滿足式（1）的一個可行解。

證明在RAAM分配算法中，對資源按照單價高低逐次分配，代碼21～24行將當前資源服務用戶從全局可用用戶里刪除，保證每個用戶最多只會租到一個資源，滿足約束條件（1a）。代碼3～7行對資源的可用用戶集篩選掉競價不高于成本價的用戶，滿足式（1b）。由于用戶按照開始使用時間排序，代碼12～18行確保當資源的兩個可用用戶使用時間沒有交集時，兩用戶之間才有路徑相連，當有交集則沒有路徑，確保一個資源一定不可能同時租給兩個有時間交集的用戶，滿足式（1c）。求解每個資源的分配方案時，在其可用用戶集合中基于關鍵路徑思想求解，最大化資源的利潤，滿足目標函數最大化。因此，RAAM求的分配方案是滿足式（1）的一個可行解。

5.2 用戶定價近似算法UPAM

RAAM求得資源分配方案后，每個租到資源的用戶需給供應商支付相應的費用。最優機制中采用基于VCG的價格支付算法，該算法時間復雜度高，且需對應最優分配算法使用才能保證機制可信。用戶定價近似算法UPAM采用二分法計算支付價格，其基于臨界值的思想，能無限逼近最低獲得分配的價格[22]，吸引更多的用戶參與拍賣，也提高了計算效率[23]。但是基礎二分法對于共享資源并不適用，其求解思想是，只要能分配到資源則更新降低競價[24]，但無限降價可能導致用戶租到了低成本的資源，不夠支付原本租的高成本資源，需對基礎二分法進行改進。設用戶j付給供應商的價格為pj，UPAM的偽代碼如算法2所示。

算法2UPAM求解用戶需要支付的價格

輸入：資源分配矩陣X，用戶集U，預約信息集Q。

輸出：各個用戶支付價格集P={p1,p2,…,pn}。

程序：

1.for eachj∈Udo

2.pj=0,cp=0

3.for eachi∈Cdo

4.Ifxij=1then /*如果j租到了資源i*/

5.cp=ei,break/*記錄j租到的資源的成本*/

6.end if

7.end for

8.Ifcp≠0then

9.h=bj,l=0 /*初始支付價格最大值h=bj，支付價格最小值l=0*/

10.while|h-l|＞εthen

11.bj=(h+l)/2

12.ifj以bj參與RAAM分配，能分配給成本單價≥cp的資源then

13.h=bj

14.elsel=bj

15.end if

16.end while

17.pj=h

18.end if

19.end for

20.returnP

UPAM算法記錄每個用戶所租資源的成本cp，不斷更新競價，判斷新價格能否給用戶分到不低于cp成本的資源。成功則降低最高競價，否則升高最低競價。不斷重復該步驟，最高和最低競價不斷逼近，最終得到用戶需要支付的臨界價格。

5.3 RAUPAM機制可信證明

定理3RAAM分配算法滿足單調性。

證明RAAM分配結束后，任意一個租到資源的用戶j，記其分配資源為i，成本單價為ei。當用戶提高自己的報價為bj′＞bj時，其他用戶請求不變，再次執行RAAM分配。資源按照單價降序排序，優先分配高成本資源，可能會出現以下兩種情況：（1）用戶j租到編號為i′∈{1,2,…,i-1}中的一個資源；（2）當（1）情況不滿足時，用戶j必然會租到i資源。

（1）求解i′資源分配方案時，其中i′∈{1,2,…,i-1}，當新的bj′＞bj時，若bj′大于i′的運行成本，j成為i′可用用戶，調用關鍵路徑算法后，j有可能租到i′資源；或者j本來就是i′的可用用戶，之前的關鍵路徑沒采用j，當提高競價后，j有可能成為i′的關鍵路徑上節點。當j租到i′資源時，用戶分配到的是比之前單價成本更高或者同成本的資源型號。

（2）（1）中的情況可能出現，當（1）情況沒發生時，在i資源分配求解中，關于j用戶的路徑都會增加，i的之前包含j的關鍵路徑也會增加，則j用戶必然會被選作關鍵路徑上的節點，租到i資源。

因此，當用戶j提高競價bj′＞bj后，用戶能分配到更高成本的資源，或者至少是同成本的資源，滿足單調性。

定理4UPAM是基于臨界值求支付價格的。

證明根據UPAM算法可知，代碼1～7行對每個租到資源的用戶j，記分配的資源成本單價為cp。初始其支付價格最大值h=bj，最小值l=0。代碼10～16行表示，當|h-l|大于設定的閾值ε時，更新bj=(h+l)/2，用戶j以新的bj參與RAAM分配，若j能租到成本單價≥cp的資源，則降低支付價格最大值h=bj，否則升高最小值l=bj。重復上述步驟，直到不滿足|h-l|＞ε時，h與l不斷逼近。最終求得用戶能分到單價為cp資源的保底價格h，作為用戶的支付價格pj。算法保證當競價bj″＞pj=h時，用戶一定能分到成本單價≥cp的資源；當用戶競價bj″＜l時，用戶一定不能分到成本單價不低于cp的資源，滿足臨界值的定義3。

定理5RAUPAM機制是可信的。

證明根據引理2，一個拍賣機制，若資源分配算法滿足單調性，且支付算法是基于臨界值的，該機制可信。在RAUPAM拍賣機制中，由定理3可知RAAM分配算法滿足單調性，由定理4可知UPAM基于臨界值求支付價格，因此RAUPAM是可信的拍賣機制。

5.4 示例

交通出行是共享經濟應用最突出的領域，本文以神州專車的預約用車為例，通過RAAM算法給各用戶分派合適的車輛，通過UPAM計算出用戶需要支付的費用。

設有兩輛車，按單位時間成本降序排序，得到車輛集合為C={1,2}，成本集合E={10,8}。按照開始用車時間對用戶排序，表1為用戶預約信息。

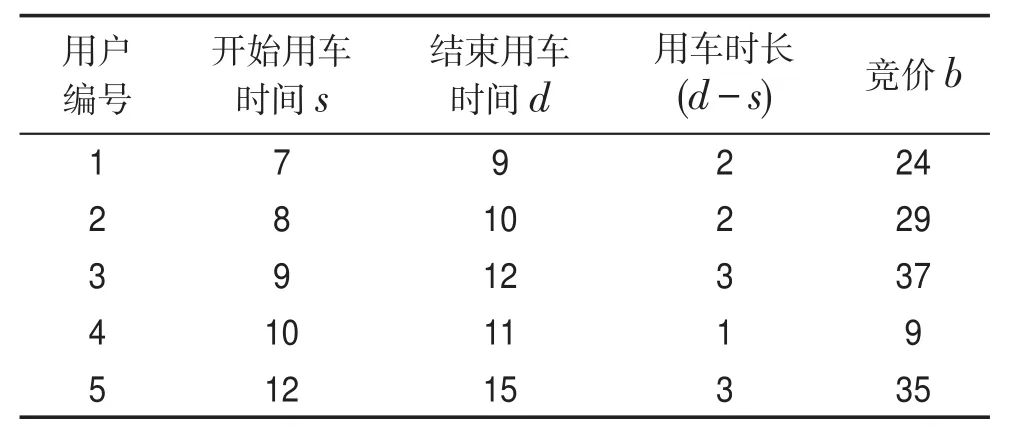
Table1 User's reservation information table表1 用戶預約信息表

（1）RAAM求車輛分配

首先對第一輛車求分配，成本單價e1=10，剔除成本≥競價的用戶4，第1輛車可用用戶集U′={1,2,3,5}。構建時間分配矩陣R，初始化每個元素為0。然后對U′中任意用戶j求r0j，如r01=b1-(d1-s1)?e1=4。再對U′中任意用戶j求元素rjk，其中k＞j,k∈U′，以r12為例，不滿足d1≤s2，不作操作；又如r13，滿足d1≤s3，r13=r03=b3-(d3-s3)?e1=7。以此類推，得到第1輛車的時間分配矩陣R，用圖表示如圖1所示。

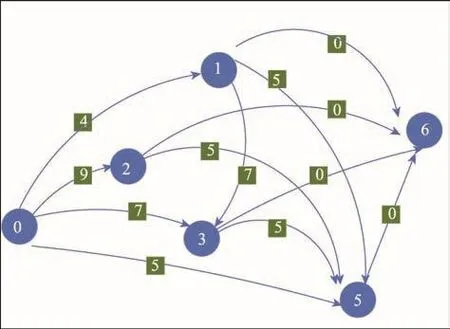
Fig.1 Time distribution diagram of vehicle 1圖1 車輛1時間分配轉化圖

對R調用關鍵路徑算法求得0到6節點的關鍵路徑為0-1-3-5-6，關鍵路徑長度為y1=16。將第1輛車分給用戶1、3和5，從可用用戶集合U中刪除這3個用戶，U={2,4}。繼續按照上述方法對第2輛車進行分配，求得第2輛車的關鍵路徑為0-2-4-6，長度為y2=14，將第2輛車分給用戶2和4。最后車輛供應商收益Y=y1+y2=30，車輛分配矩陣X如表2所示。

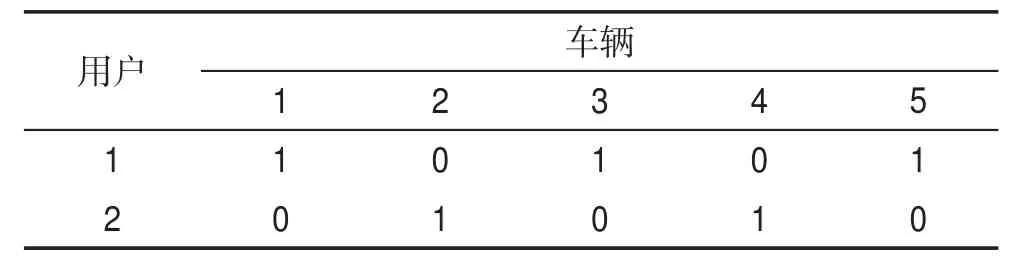
Table2 Vehicle allocation matrixX表2 車輛分配矩陣X

（2）UPAM計算支付價格

需要為每個分到車的用戶計算支付價格。本示例中設置閾值ε=1，所有計算結果向下取整。以求解1用戶支付價格為例。用戶1租到第1輛車，成本參數cp=e1=10，初始h=b1=24，l=0。|h-l|=24＞ε，更新競價b1=(h+l)/2=12，重新運行RAAM，此時用戶1不能分到成本不低于cp=10的車，因此令l=b1=12。由于h=24,l=12，|h-l|=12＞ε，更新b1=(h+l)/2=18，重新進行RAAM。重復運行RAAM，若用戶1能分到成本不低于cp=10的車，則h=b1；若不能則l=b1，不斷更新b1=(h+l)/2，直到 |h-l|≤ε，計算結束。最終取新的h作為用戶的支付價格，最后求得用戶1需支付p1=h=22。

6 實驗

6.1 實驗設置

本文采用真實的出租車數據模擬預約用車數據，反映用戶的真實用車需求，以此來測試本文提出的算法對于共享經濟預約模式下資源的分配結果。實驗數據包含每輛車在不同時間點的經緯度、速度、載客狀態等信息。根據車輛編號，對每輛車按照時間從早到晚排序，選取了2007-01-31日12：00—24：00半天的數據，并剔除了冗余的數據。實驗設置如下。

（1）得到的信息中沒有價格及車型等信息，實驗采用神州專車預約平臺的車型數據，共有三種車型，每分鐘單價平均為8、6、4元，三種車型各占1/3。用戶的競價=用車時間×（5到10之間的隨機數），即用戶競價與用車時長相關。

（2）不失一般性，實驗分為小、中、大三種規模。

（3）實驗設置不同密度，分別模擬不同的競爭情況，以分析各種情況下算法的執行效果。

（4）設置不同分配周期，并分析周期對分配的影響。

（5）實驗環境：實驗搭建在 Intel?i7-6700 CPU 3.40 GHz,8 GB內存平臺。

實驗采用三種主流算法與本文算法進行對比。（1）CPLEX求解器的最優算法。通過編寫規劃模型，在求解器CPLEX上求出最優解。但CPLEX十分消耗內存，幾百個用戶的約束條件就會導致內存耗盡，基本只能解決小規模下的分配。（2）先預約先服務算法（first-come-first-serve，FCFS），按照預約順序給用戶安排車輛，算法實現簡單，這是目前專車預約平臺采用的分配方式。（3）最高出價優先算法（MAXBID）。利用貪婪法的思想，總是選取當前競價最高的用戶，使得局部收益最大化，但局部最優并不能實現全局最優。

6.2 結果分析

實驗將對CPLEX求解的最優算法、提出的RAUPAM算法、FCFS、MAXBID算法進行以下三方面的評估。第一，多維度分析算法效果。實驗首先選取了三個有代表性的密度0.8、2.0、4.0，來分別模擬低峰期、正常時期、高峰期的情況，以分析各種情況下算法的執行效果。然后實驗分三種不同的周期T4、T6、T12對車輛進行分配，并將各周期結果分別加和以分析長短周期對分配產生的影響。第二，評估指標。在同種密度和周期下，本文從平臺利潤、服務用戶率、車輛時間利用率對算法進行評估。第三，不失一般性。為了降低數據對結果的影響，實驗分為小規模（10輛車）、中規模（100輛車）、大規模（1 000輛車）三種情況，從不同的規模對本文算法進行評估。

6.2.1 密度對算法執行效果的影響

在不同的時期，資源競爭情況也不同。如對于車輛的預約來說，在上下班高峰期，車輛資源稀缺；在白天其他時間段，車輛基本可以滿足所有用戶的請求；在晚上，車輛又大量閑置。對于共享經濟中的其他資源，也同樣存在使用高峰期和低峰期。實驗選用T6第一個周期的數據，設置了三種密度，0.8、2.0、4.0，并分析不同密度下算法的執行效果。

圖2通過展示三種密度下服務用戶率的差別，這三個密度可分別用來代表不同的資源競爭情況。在0.8密度下，平均將8輛車的用戶分配給10輛車，車輛富余，幾乎所有算法的服務用戶率都是1.0，可以用來模擬低峰期的情況。2.0密度下，平均將20輛車的用戶分給10輛車，雖存在競爭，但車輛基本能滿足用戶的需求，所有算法的服務率都能達到90%以上，用來模擬正常時期。4.0密度下，平均將40輛車的用戶分配給10輛車，車輛供不應求，服務用戶率只能達到50%左右，可用來模擬高峰期。

圖3在三種密度下，對比了各算法得到的利潤。任何一種規模下，密度越大，利潤越大，證明高峰期能為供應商帶來更多的利潤。在小規模時，CPLEX的利潤是最高的，但隨著密度增大，CPLEX的增長速率逐漸緩慢；而RAUPAM的利潤一直勻速增長，隨著密度的增大，與CPLEX的差距逐漸縮少，體現了RAUPAM算法在高峰期時表現優異。

Fig.2 Comparison of service user rates of different algorithms under different densities圖2 不同算法在不同密度下的服務用戶率比較

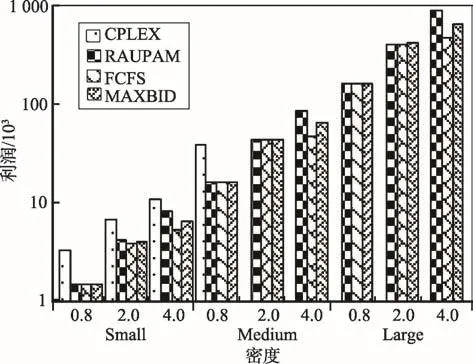
Fig.3 Profits of different algorithms under different densities圖3 不同算法在不同密度下的利潤比較

接下來比較RAUPAM、FCFS、MAXBID三種算法受密度的影響程度。在任意一種規模下，0.8密度時，車輛資源充足，三種算法都能使得幾乎所有用戶得到服務，利潤幾乎相等。到了2.0密度時，三種算法差別不大，按照利潤大小排序為RAUPAM>MAXBID>FCFS。到了4.0密度時，三種算法差距增大，RAUPAM是利潤最大的，比FCFS平均高出75%，比MAXBID算法平均高出30%。因此在任意密度下，即高峰期和低峰期時，RAUPAM都是三種算法中利潤最大的，尤其在高峰期優勢更明顯。

任意規模下，RAUPAM算法的利潤都隨著密度的提高而勻速增長，而FCFS和MAXBID算法的利潤增長速率隨密度增長逐漸變小，其中FCFS算法減小得更多。證明在不同密度下，即是高峰期和低峰期，RAUPAM算法都表現穩定，不受密度影響；而FCFS和MAXBID算法在高峰期執行效果變差。因此RAUPAM為共享經濟供應商在高峰期和低峰期都能提供更優的資源配置方案。

6.2.2 周期對算法執行效果的影響

本文提出的機制用于共享經濟預約模式下做資源配置，預約模式下用戶在使用時間之前提出預約請求，機制按周期對資源進行分配，用戶需在周期開始前提交預約請求。但是具體周期時長應如何確定，是一個復雜的問題。因為共享經濟中的資源使用時間特點不同，周期應不同。如對于共享住宿，周期以天為單位；而預約掛號，應以分鐘為單位。周期應能包含多數用戶的使用周期，避免周期過短而淘汰大量跨周期用戶。但周期過長，雖然能包含大量用戶的請求，又需要用戶更早做預定。

本文設置了三種不同的周期，分析周期對于RAUPAM、FCFS、MAXBID這三種算法的影響。實驗采用的是2007-01-31日12：00—24：00半天的數據，密度采用4.0，設置了三種不同的周期：短周期，4 h周期（T4），共有3個周期；中周期，6 h周期（T6），兩個周期；長周期，12 h周期（T12），1個周期。實驗將T4的3個周期的利潤加和，T6的兩個周期利潤加和，與T12周期的利潤進行比較。

如圖4所示，在同種規模的不同周期下，各種算法的周期利潤總和差別不大，因此周期對算法的利潤影響不大。對于RAUPAM算法來說，相同規模下，周期越長，得到的利潤總和越大，即T12>T6>T4，因此在條件允許的情況下，盡量提醒用戶提前預約。這是因為RAUPAM算法對車輛進行時間資源規劃，周期越長，每輛車的可選用戶增多，就能規劃出更優的配置方案。FCFS和MAXBID算法受周期影響利潤值有所波動，如小規模下，FCFS算法在T6的利潤和最大，但在中規模時，又是T12利潤和最高。RAUPAM隨周期增長收益在小幅增加，表現穩定；而FCFS和MAXBID隨周期變化收益波動，易受周期影響。

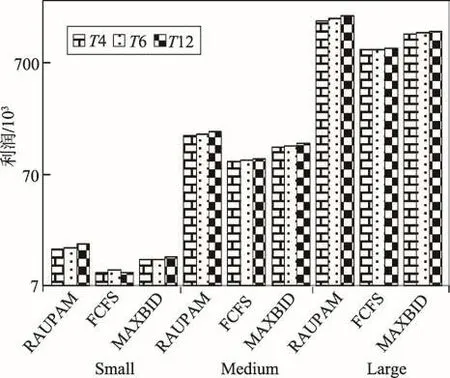
Fig.4 Comparison of profits of different algorithms under different cycles圖4 不同算法在不同周期下的周期利潤和比較

在同種規模下，無論RAUPAM的周期選T4、T6、T12，RAUPAM的周期利潤和都遠高于FCFS和MAXBID的三種周期中的最高值，即無論選取任何一種周期做分配，RAUPAM算法都比FCFS和MAXBID有明顯的優勢。雖然共享經濟中資源的使用周期不盡相同，以天、小時、分鐘為單位，但RAUPAM算法不受周期影響，在長短周期都表現優異，適合為不同分配周期的共享資源做優化配置。

6.2.3 四種算法詳細比對

實驗對四種算法從平臺利潤、服務用戶率、車輛時間利用率這三個指標進行詳細對比分析。選取T6第一個周期的數據，密度采用4.0。

（1）平臺利潤

社會福利是常用來衡量機制的重要指標，但是社會福利是各個勝出拍賣用戶的競價之和，社會福利最大不代表利潤最大（選取多數使用時間長的用戶），而利潤才是供應商最關心的指標。本文所有算法的目標為平臺利潤最大化，并對四種算法從利潤方面進行對比。表3詳細展示各種規模下的車輛數目與4.0密度下對應的用戶數目，列出四種算法在三種規模下得到的利潤值，并將FCFS和MAXBID算法的收益值與RAUPAM算法進行比對，得到RAUPAM對這兩種算法在利潤方面的提升率。

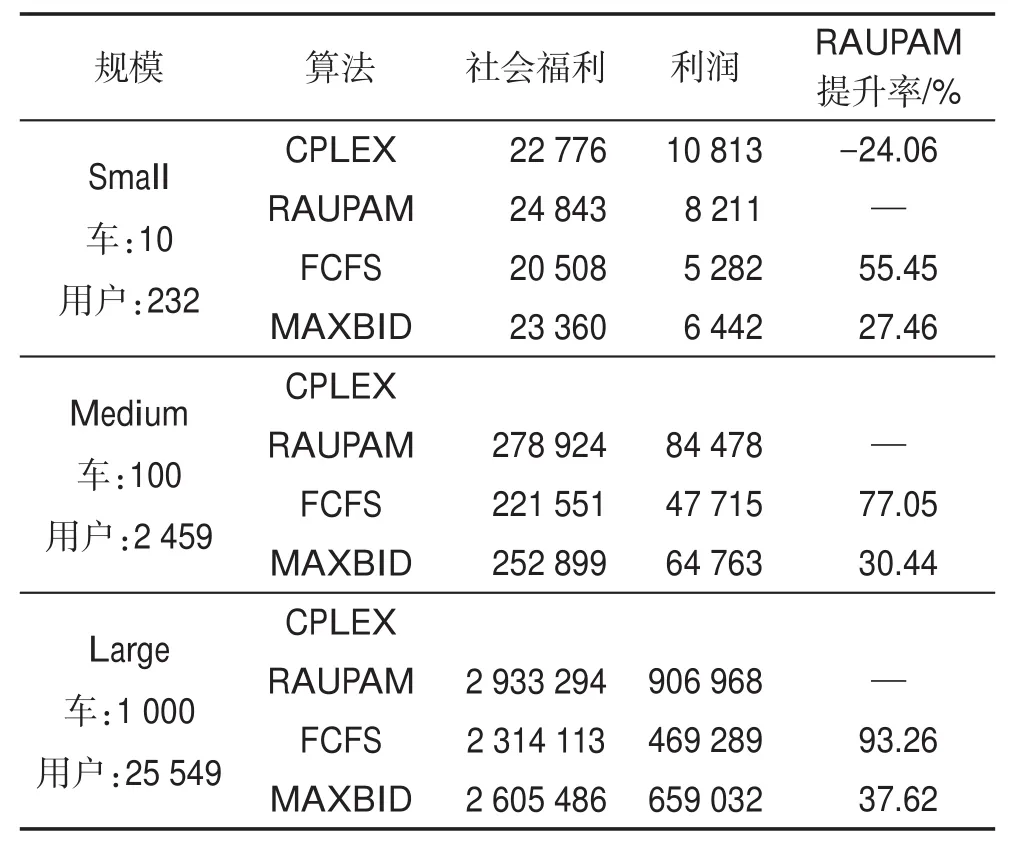
Table3 Experimental result表3 實驗結果表

如表3所示，在小規模下，RAUPAM的利潤與CPLEX最優算法的利潤值最接近，達到CPLEX最優解的75%左右，而另外兩種算法只能達到50%左右。當車輛數目在10以上，用戶數目超過500時，約束條件數目過大，CPLEX求解內存空間不夠導致無法求解，而其他三種算法在大規模時仍然能快速求解。在中、大規模下，RAUPAM算法得到的利潤是最大的，從最后一列可以看出，RAUPAM算法對于FCFS和MAXBID算法有顯著的提高。

四種算法中，FCFS的利潤最差，這是因為用戶預約請求時間的不確定性，先預約的用戶可能占用時間長且利潤低，導致后預約的用戶雖然能帶來更大利潤卻預約不成功。隨著規模的擴大，RAUPAM算法的優勢比FCFS更明顯，如從小到大規模時，RAUPAM在利潤方面比FCFS的提高率從55%到77%，再上升到93%，幾乎是其兩倍。

MAXBID采用貪婪的思想，選取當前競價最高的用戶，因為不知道能分配到何種車型，成本不固定，所以沒有采用利潤最大優先算法。這種局部選取最大競價的思想，卻并未實現全局競價最優。表3中社會福利即等于競價之和，MAXBID在每種規模下的競價之和并沒有RAUPAM的高。MAXBID對于規模不太敏感，一直表現較穩定，但是隨著規模增大，RAUPAM比MAXBID算法在利潤方面的優勢在小幅提高。RAUPAM的利潤比MAXBID算法平均高30%左右。

RAUPAM算法從全局考慮資源的分配，優先讓高成本車輛選取出價高的用戶，其淘汰的用戶能繼續租到低成本車輛，最大化資源的利用。在計算每個車輛的分配方案時，對該車可用用戶調用關鍵路徑算法，求得對用戶集的最優分配方案，最大化該車的利潤，因此RAUPAM的利潤比FCFS和MAXBID有顯著提高。小規模時，CPLEX的競價之和不是最大，利潤卻是最高，其成本是四種算法中最低的，因為其優先給每個用戶分配低成本的車型以獲得更大的利潤。但RAUPAM算法優先為用戶分配滿足成本的高檔車輛，出價高的用戶優先分到好的車型，滿足公平性且提升了用戶的滿意度。

（2）服務用戶率

當車輛資源緊缺時，算法應該在符合利潤最大化的前提下滿足更多用戶的預約請求，服務用戶率等同于用戶預約訂單成功率，直接影響用戶的體驗度，是共享經濟租賃平臺關注的另一重要指標。

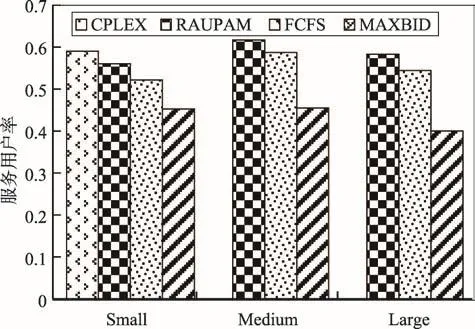
Fig.5 Comparison of service user rates of different algorithms圖5 不同算法的服務用戶率比較

圖5 從服務用戶率的維度對四種算法進行對比分析。在小規模時，CPLEX算法的服務用戶率是最高的，達到59%，RAUPAM算法其次，達到56%。在所有規模下，RAUPAM、FCFS、MAXBID這三種算法中，RAUPAM算法的服務率都是最高的，FCFS其次，RAUPAM的用戶服務率平均比FCFS提高了7%左右；MAXBID的服務率最低，RAUPAM的服務用戶率比其平均提高了20%～30%。當前密度為4，車輛資源稀缺，RAUPAM的服務用戶率維持在60%左右，使得盡可能多的用戶請求得到了滿足。MAXBID服務用戶率最低，平均只有43%左右，因為其遵循出價最大選擇用戶，選取大量使用時長的用戶占據了資源，使得車輛能服務的用戶數減少。

（3）車輛時間利用率

4.0密度下，車輛對于用戶供不應求，每輛車都會被用到，計算車輛利用率沒有意義。而車輛時間利用率是根據每種算法服務用戶的時間加和，并除以所有車輛的可用時間之和，更能反映車輛資源的使用情況。圖6從車輛時間利用率方面對四種算法進行了對比。

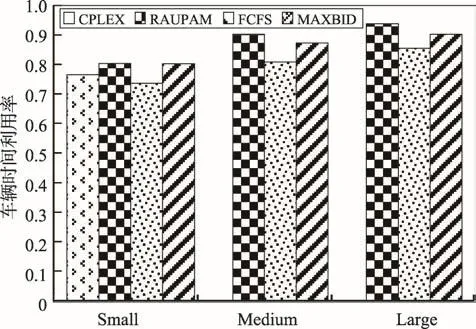
Fig.6 Comparison of utilization rates of vehicle time of different algorithms圖6 不同算法的車輛時間利用率比較

如圖6所示，在任意規模下，RAUPAM算法的車輛時間利用率都是最高的，在小規模時都高于CPLEX算法。隨著規模的擴大，各算法的車輛時間利用率增加。RAUPAM算法的平均車輛時間利用率高達88%，因為算法對每輛車做規劃，減少碎片時間，提高了車輛資源的利用率。FCFS的車輛時間利用率是所有算法中最低的，平均只有79%。FCFS按照用戶預約申請順序來進行車輛的分配，先預約的用戶占住了時間，產生大量碎片時間，導致車輛時間利用率低。

實驗結論：通過比較密度對于算法的影響，發現在高峰期和低峰期，RAUPAM的利潤都大于FCFS和MAXBID，且表現穩定不受密度影響；而FCFS和MAXBID算法在高峰期表現較差，因此RAUPAM為共享經濟供應商在高峰期和低峰期都能提供更優的資源配置方案。通過分析周期對算法的執行影響，發現在同種規模下，無論RAUPAM的周期選T4、T6、T12中的任意一種，RAUPAM得到的周期利潤和都遠高于FCFS和MAXBID的三種周期中的最高值。因此RAUPAM算法不受周期影響，在長短周期都表現優異，適合為不同周期的共享資源做優化配置。同周期同密度下，對四種算法進行了更詳細的比對。無論何種規模下，RAUPAM算法的利潤都顯著大于FCFS和MAXBID，比FCFS至少提高55%，比MAXBID算法平均提高30%。在服務用戶率方面，RAUPAM算法的服務用戶率平均達到60%，比FCFS平均提高7%，比MAXBID平均提高了20%～30%，保證大多數用戶能得到服務。任何規模下，RAUPAM算法的車輛時間利用率都是最高的，平均高達88%，達到了較高的資源利用率。

7 結束語

針對目前共享經濟預約模式采用固定價格及先預約先服務分配資源的方式，存在的供應商收益低下、資源利用率不高等問題，本文設計可信的拍賣機制用于解決共享經濟預約模式中資源的分配及用戶定價問題。

本文對共享經濟預約服務中資源的分時租賃問題建模，并設計可信的最優拍賣機制，用CPLEX求解最優資源分配方案，基于VCG理論計算用戶的支付價格。但最優機制無法在多項式時間求解，提出可信的啟發式機制RAUPAM解決大規模的資源租賃分配及用戶定價問題，用關鍵路徑的思想求解近似最優分配方案，再用二分法求用戶的支付價格。測試結果表明，RAUPAM比傳統算法FCFS和MAXBID取得了更好的結果。

本文提出的拍賣機制，適用于任何按時收費的共享資源在預約模式下做分配，如共享停車位、共享住宿、共享廚房等；也適用于其他按時使用收費的資源，如云平臺中資源的分配、醫療診治預約等。但在實際共享經濟市場中，還有一些可移動的共享資源，用戶可在不同的地點分別領取和歸還資源，其收費與取還點相關，如共享充電寶、共享服裝等。在未來的研究工作中，將設計適用于這些可移動資源預約的拍賣機制，將取還點納入參考因素，從全局決策這些資源預約模式下的租賃分配方案。