非線性振動下水平通道內氣液兩相流動研究

周云龍，常 赫

(東北電力大學 能源與動力工程學院，吉林省 吉林市 132012)

兩相流運動廣泛存在于能源、核能、動力、石油、海洋等多種工業領域中，因此預測兩相之間復雜的自由界面運動有很大研究價值。近年來隨著科學技術向水下潛艇、漂浮式核能設備以及航天領域的深入研究，國內外專家和學者在實驗上和數值模擬上對動態條件下管道內流動特性的研究正在逐步開展[1-4]，并取得了一定研究成果。然而因地震等引起的非線性振動條件下的兩相流現象尚未得到統一的結論，特別是與反應堆安全相關的研究更是鮮有報道。

在工程實際中，振動工況會引起乏燃料水池、池式快堆、沸水堆堆芯等的自由界面產生振動現象并沖擊管道壁面，從而影響組件結構和完整性，及流體與結構間的傳熱性能，進而影響設備的壽命和安全運行[5-7]。因此，對動態工況下流體流動情況的研究對確保核反應堆安全運行具有十分重要的實際意義。

隨著計算機技術的發展，數值模擬作為一種重要手段廣泛應用于各類研究中。由于氣液兩相界面密度及壓力等存在巨大差異，關于氣液兩相流的數值模擬一直是流動模擬的熱點，其研究重點是運動界面的追蹤以及邊界條件的構造[8]。由于通道結構與流體間流固耦合作用的復雜性，對于振動通道內氣液兩相流動的數值模擬則是少之又少。

基于上述原因，本文通過實驗方法研究非線性振動狀態下的氣液兩相流型及流型轉換界限。同時利用FLUENT框架對振動通道運動進行剖析后，使用CLSVOF(coupled level set and volume of fluid)方法建立正弦振動下水平通道內氣液兩相流動數值模擬模型，模擬研究相應工況下流體的流動情況，為后續動態條件下管內傳熱及兩相流動的數學模型奠定基礎，以期對振動狀態下設備管道的安全運行起到一定的指導作用。

1 實驗裝置及原理

本實驗將如圖1所示的兩相流實驗回路與振動裝置相結合，對水平通道內氣液兩相流進行研究分析，實驗裝置介紹及實驗步驟詳見文獻[9]。實驗段采用管徑為35 mm、長度為2 m的透明有機玻璃管，將其水平固定于振動臺上，如圖2所示。兩個測壓孔分別位于實驗段兩端，并與壓差變送器相連，通過數據采集系統采集數據。實驗在常溫、常壓下進行，振動臺的非線性振動形式按正弦規律Z=Asin(wt)=Asin(2πft)振動，其中A為振幅，f為振動頻率，Z為瞬時位移，w為角速度，t為時間。氣體體積流量范圍為0.2～60 m3/h，液相體積流量范圍為0.3～7 m3/h，利用高速攝影儀記錄氣液兩相流型。

圖1 實驗系統示意圖Fig.1 Schematic diagram of experimental apparatus

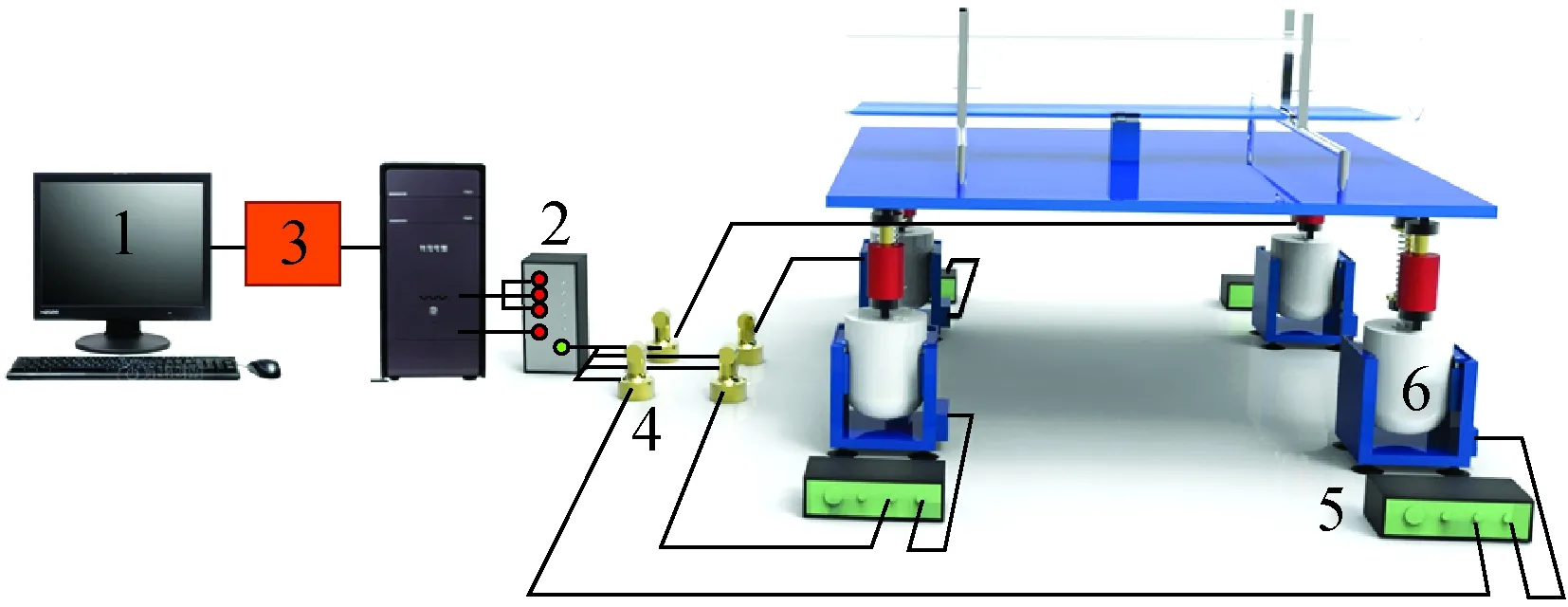
1——工業控制計算機；2——并行采集通道； 3——異步協同控制器；4——電容傳感器； 5——數字式開關功率放大器；6——電磁振動裝置圖2 非線性振動實驗臺Fig.2 Test bench of nonlinear oscillation

2 數值計算

2.1 控制方程

數值計算方法采用CLSVOF方法對氣液兩相流界面進行追蹤，其基礎控制方程詳見文獻[10]。針對本文的動態工況，為解決體積分數α的遷移問題，依據Weller引入的額外人工壓縮項[11]，將體積分數函數方程發展為：

(1)

式中：u為流體速度；ur為只對界面產生影響的適于壓縮界面的速度場[12]，本文將其處理為兩相流體的速度差。

對于正弦振動工況下兩相流控制方程，采用連續性方程和考慮表面張力的Navier-Stockes方程，基本方程詳見文獻[13]。針對系統在振動狀態下所發生的頻率很高的微小位移變化，本文假定通道以相同的速度ud運動，此時，流體速度u可看作由兩部分組成：通道振動速度ud及感應速度uc。此時動量方程發展為：

(2)

式中：ρ為流體密度；p為通道壓降；g為重力加速度；μ為流體黏度；Fσ為Brackbill等[14]提出的表面張力模型。ud可通過位置變化求得。因uc是非空間變化的，這里依據文獻[7]采用假設：

(3)

2.2 數學模型

本文依照實驗數據使用PRO.E進行幾何造型，進口管徑r0為27 mm，壁厚w0為5 mm，通道直徑r1為35 mm，管長L為2 m。利用ICEM進行網格劃分，對通道壁面附近網格進行邊界層細化處理，然后將網格導入ANSYS FLUENT 15.0進行三維計算。模擬工況前，對網格進行無關性驗證，研究發現網格數對壁面壓力幾乎沒有影響，與Lim等[15]得出的結論一致。因此，通過比較不同網格劃分時穩態工況下通道內彈狀流的氣泡長度，最終確定本文采用網格數為396 000的非結構化四面體網格進行計算。幾何模型及網格劃分如圖3所示。

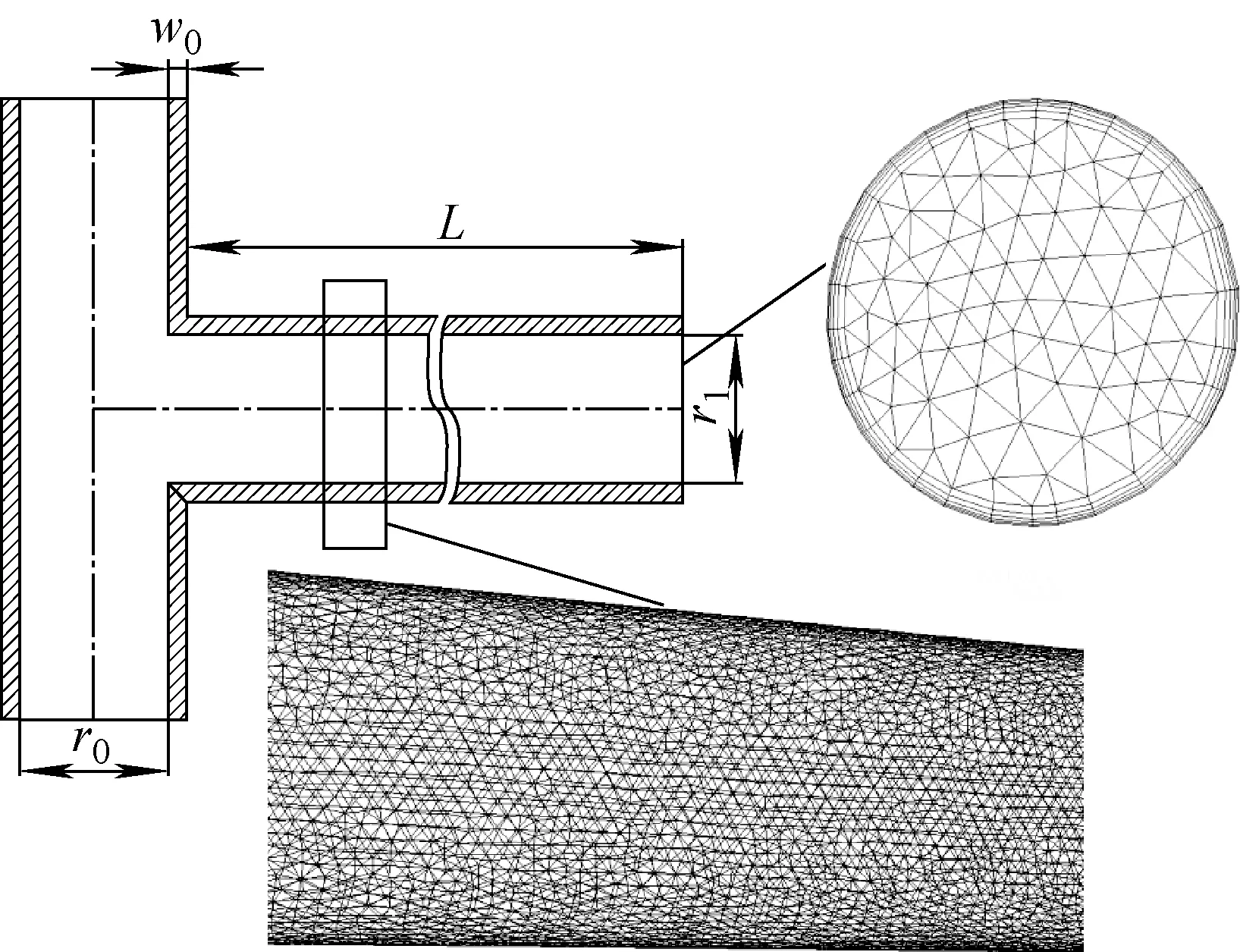
圖3 幾何模型及網格劃分Fig.3 Geometric model and mesh geometry

計算過程中，在有限體積法的框架下，采用時間非穩態計算方法，對動量時間方程采取二階隱式格式，對流項和黏度擴散項采用二階迎風格式。利用UDF編程手段，在動網格模型下實現正弦振動工況下的模擬，其他相關邊界條件設置參考文獻[16]。每次模擬過程中，為保證收斂，需適當調整時間步長和松弛因子。

2.3 數值方法驗證

管內氣液兩相流動情況隨實驗段的非線性運動不斷發生變化，借助高速攝影儀觀察實驗段內流體流動情況可發現，振動狀態下水平通道內氣液兩相流型主要有泡狀流、彈狀流、攪拌流、波狀流及環狀流。為驗證本文所采用數值方法的可靠性，以振幅為2 mm、振動頻率為5 Hz的振動工況為例對數學模型進行驗證，模擬條件與文獻[17]中的實驗一致，其中氣相表觀速度jG的變化范圍為0.015～12 m/s，液相表觀速度jL的變化范圍為0.02～2.5 m/s。根據大量實驗和模擬結果，繪制了如圖4所示的流型圖，針對流型定性驗證過程，本文以彈狀流及波狀流為例示于圖4，可發現數值模擬與實驗得出的流型特征基本一致。

圖4 流型圖比較Fig.4 Comparison of flow regime

非線性振動通道內的摩擦壓降Δp可表示為：

Δp=Δpf+Δpg+Δpa

(4)

式中：Δpf為摩擦壓降；Δpg為重位壓降；Δpa為加速壓降。由于本文采用水平通道，故Δpg=0；實驗研究為常溫條件下流體流動，故Δpa=0。

為定量驗證數值方法的可靠性，針對振動工況下通道內的摩擦壓降進行了測量，并與模擬結果進行對比。與此同時，為探討非線性振動對通道內氣液兩相流動的影響，本文對相同工況下穩定通道內的摩擦壓降也進行了測量與計算。實驗與數值計算摩擦壓降的對比如圖5所示，進一步證明了本文所選取的求解算法可正確反映非線性振動工況下通道內氣液兩相的流動情況。圖5中，Δpfs為穩定狀態下的摩擦壓降，Δpfos為振動狀態下的摩擦壓降。

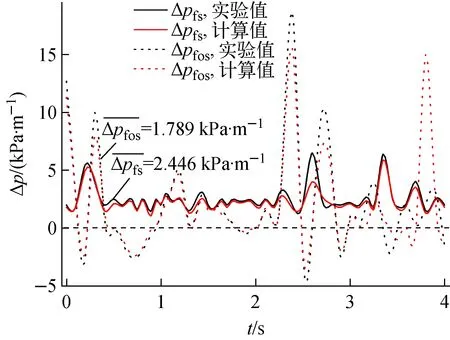
圖5 實驗與數值計算的摩擦壓降對比Fig.5 Frictional pressure drop comparison between experiment and numerical simulation

3 結果及分析

3.1 非線性振動對流型的影響

通過對高速攝影儀所采集的正弦形式振動通道內各工況下氣液兩相流動圖像進行分析可發現，與穩定通道內兩相流流型特征相比，振動通道內流體的流動情況在氣液兩相界面分布及不同流型間轉換界限等方面均存在一定差異。實驗過程中，除一些公認的水平通道內流型如彈狀流、波狀流、環狀流等存在不同外，也發現了幾種不同于常規通道的流型。以穩定狀態下的彈狀流和分層流為例，對穩態與非線性振動下通道內流體流動進行對比，如圖6所示。

由圖6可見，非線性振動條件下，彈狀流氣液兩相界面面積會發生變化，相應影響流型特征。穩定狀態下的長氣彈在振動的影響下，被分割成諸多由小氣泡包圍的小氣彈，隨通道的非線性振動間歇性接觸通道壁面，或衰減為小氣泡，或形成新氣彈，從而形成異于常規靜態通道的彈狀流。與此同時，非線性振動對穩態通道內的典型流型分層流也有很大影響。觀察圖6發現，非線性振動通道內氣液兩相流動情況近似于波狀流，但氣液兩相界面振動的波紋更加強烈，且在整個通道液相內部都存在大量小氣泡。

正弦振動過程大體可分為兩部分：在向上振動的過程中，通道內液相受到向上振動時所產生的附加力和自身的重力，此時氣相對界面產生的剪切力及管壁產生的阻力不能抵消液相所受到的斜向上方向的合力，從而對液相向上運動的趨勢無法造成影響；然而在通道向下運動的過程中，其斜向下方向的合力加速了液相向下的運動趨勢。換個角度來說，非線性振動相當于給近壁區域流體施加了一沿振動方向上的速度，這樣流體的速度就變成原有速度與振動引起的附加速度的合成。綜上所述，振動引起的附加慣性力及流體自身重力使得通道內流體流動變得更加復雜，特別是氣液兩相流速較低時。與之相比，非線性振動對高流速流體的流型影響較小，通道內流型與穩態工況類似。

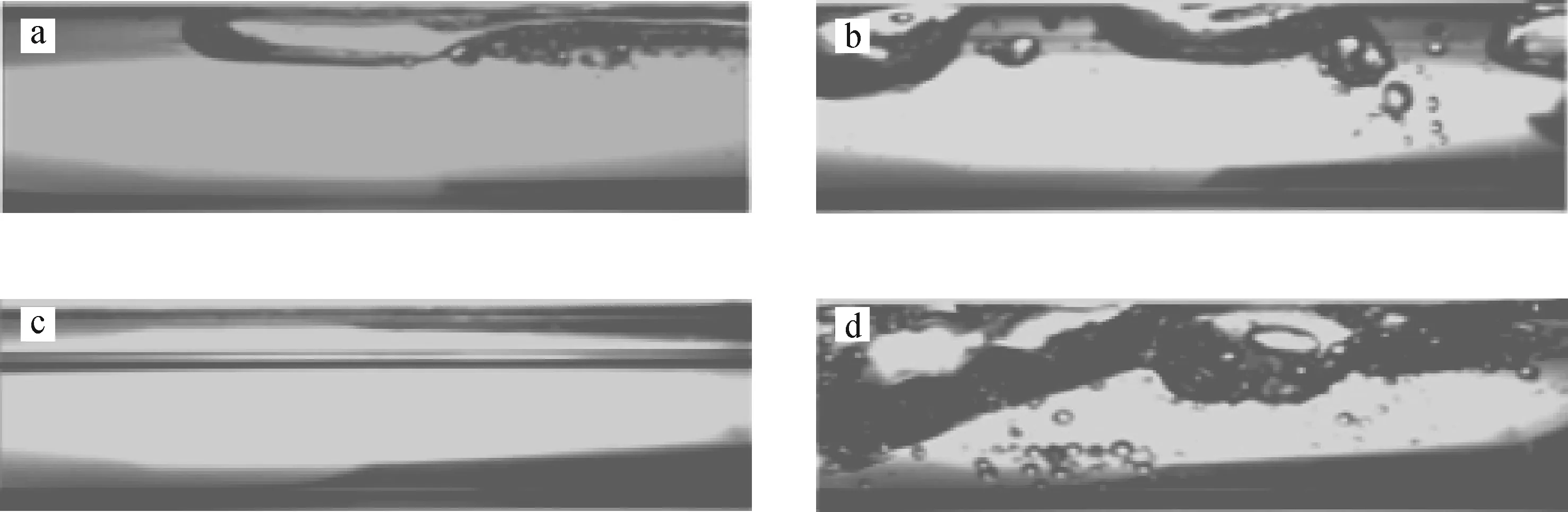
a、b——彈狀流，jG=0.09 m/s，jL=0.5 m/s；c、d——分層流，jG=0.1 m/s，jL=0.1 m/sa、c——穩定狀態；b、d——非線性振動狀態圖6 典型流型對比Fig.6 Comparison of typical flow regime

3.2 非線性振動對摩擦壓降的影響

如圖5所示，與穩定狀態下通道內氣液兩相流體瞬時摩擦壓降相比，非線性振動狀態下通道內壓差波動信號較為劇烈，波動信號變化頻率較快，且具有更大的波動幅值。其原因在于非線性振動引起的流動不穩定性與管內氣液兩相流體的相對運動共同影響了壓差波動信號。然而穩定狀態下通道內的平均壓降梯度為2.446 kPa/m，非線性振動狀態下為1.789 kPa/m，減小了36%。為進一步探討非線性振動對通道內氣液兩相流動的影響，本文采集了不同Re下的摩擦壓降，結果如圖7所示。圖7中，λ為摩擦阻力系數。由圖7可看出，瞬時摩擦壓降波動規律與Re關系不大，因此不能通過Re的大小判斷摩擦壓降的大小。然而，通過比較不同流速下摩擦壓降峰值出現的時間，可發現流速越大峰值出現越晚。同時λ隨Re的增大而減小，說明非線性振動狀態下平均摩擦阻力系數依然和Re呈反比。

圖7 Re對摩擦壓降的影響Fig.7 Effect of Re on frictional pressure drop

與此同時，為進一步探討非線性振動相關參數對通道內氣液兩相流動的影響，本文對相同流速下不同振動參數時的摩擦壓降進行了模擬計算，結果如圖8所示，其中A2f2代表振動幅度為2 mm，振動頻率為2 Hz。由圖8可見，振動參數對摩擦壓降具有一定影響。當振動頻率從2 Hz增至16 Hz時，瞬時摩擦壓降波動幅度從-207.2%～344.3%變化至-203.9%～405.3%，幅值增加10.4%左右，說明振動頻率對瞬時摩擦壓降的波動幅度及頻率均有較為顯著的影響；當振動幅度從2 mm增至10 mm時，瞬時摩擦壓降的波動幅度從-132.2%～309.7%變化至-155.8%～324.9%，幅值增加6.8%，說明振動幅度對摩擦壓降無明顯影響。

對此現象進行分析如下。通常情況下，穩定狀態下通道內氣液兩相流動壓降受到壁面性質和Re的影響，與之相比，當通道做非線性振動時，在通道壁面很薄的區域內會產生瞬時的脈動渦流及巨大的脈沖速度，同時由于這一區域的非線性相互作用，從而破壞了壁面附近流動邊界層。振動幅度和頻率越大，對原有流場影響越大，流動越紊亂，流線偏離原流動方向的程度越大，相應迅速增大流場靜壓。

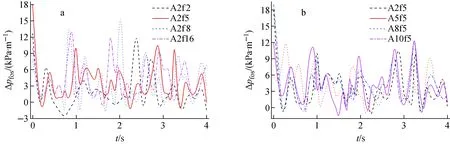
圖8 振動頻率(a)和幅度(b)對摩擦壓降的影響Fig.8 Effect of vibration frequency (a) and vibration amplitude (b) on frictional pressure drop

區域振動時，流場結構會發生變化，流動速率也會隨振動參數的改變而改變。小振幅低頻率時，流動速率上升緩慢，同時大尺度旋渦變成小尺度，小尺度旋渦破碎進而隨主流運動；大振幅高頻率時，流動速率迅速增大，大尺度旋渦也會發生破碎，直至被主流帶走。因此，高頻率時通道摩擦壓降變化更加明顯。

綜上所述，對非線性振動通道內氣液兩相流動行為的把握對確保核反應堆安全具有十分重要的實際意義。

4 結論

本文通過將實驗與數值模擬相結合的方式，對非線性振動水平通道內氣液兩相流動行為進行了探討與研究，得出如下結論。

1) 常溫常壓條件下，非線性振動工況下水平通道內氣液兩相流型與穩態時有所不同，主要流型有泡狀流、彈狀流、攪拌流、波狀流及環狀流。

2) 與穩定狀態下水平通道內氣液兩相流相比，非線性振動狀態下會出現更復雜的氣液界面，且瞬時摩擦壓降波動較大，平均摩擦阻力系數與Re呈反比。

3) 瞬時摩擦壓降波動規律與Re關系不大，然而通過比較不同流速下摩擦壓降峰值出現的時間，可發現流速越大峰值出現得越晚。

4) 非線性振動狀態下，瞬時摩擦壓降的波動幅度與振動參數的變化呈正比，與振動幅度相比，振動頻率對其影響高出4%。