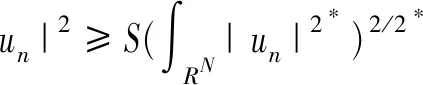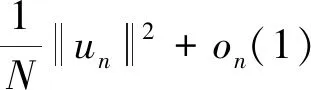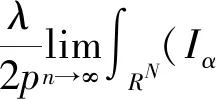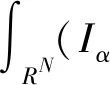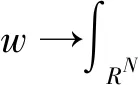帶有臨界項的Choquard方程的基態解
龍 雷,黃永艷
(山西大學 數學科學學院, 太原 030006)
本文主要考慮下面的Choquard方程[1-9]:
-Δu+u=λ(Iα*|u|p)|u|p-2u+
|u|2*-2u,x∈RN
(1)
其中:N≥3;α∈(0,N);λ>0;p是介于上下臨界之間且不包含上下臨界的數,上臨界是指(N+α)/(N-2),下臨界是指(N+α)/N。Iα是一個Riesz勢函數,即
若λ=1,且沒有臨界項,方程(1)是Choquard-Pekar方程:
-Δu+u=(Iα*|u|p)|u|p-2u
x∈RN
(2)
當N=3,α=2,p=2時,方程(2)描述了帶電粒子與未知電磁場之間的相互作用,在天體力學、量子力學、統計物理學中都有廣泛的應用,可參考文獻[4,9]。Lieb[1]和Lion[2]最早證明了方程(2)非平凡解的存在性。目前,已經有一系列關于Choquard-Pekar方程的結果,可參考文獻[5]。
Seok[3]用擾動理論證明了下面Choquard方程徑向對稱解的存在性:
-Δu+u=(Iα*|u|p)|u|p-2u+λ|u|2*-2u
其中x∈RN。最近,Schaftingen等[6]證明了當非線性項f(x,u)=f(u)滿足一定條件時,下面Choquard方程基態解的存在性:
-Δu+u=(Iα*|u|(N+α)/N)|u|(α-N)/Nu+f(x,u)
x∈RN
受上述結果的啟發,本文研究當λ≥λ0時,Choquard方程(1)基態解的存在性。
定理1存在λ0>0,使得對于所有的λ≥λ0,Choquard方程(1)有一個基態解。
在定理1中得到的基態解是指相應能量泛函的所有非平凡臨界點中使能量泛函能量達到最小的那一個,也就是極小化問題
m=inf{J(u):u∈H1(RN){0},J′(u)=0}
(3)
可達時對應的極小值點。
1 準備工作與能量估計
記Lq(RN)中的范數為|·|q,Ck表示不同的正常數,R+=[0,∞)。
工作空間是Sobolev空間H1(RN),它的標準范數是
▽u|2+u2])1/2
H1(RN)連續嵌入Lq(RN),q∈[2,2*]。因此,對每一個q∈[2,2*],存在一個正常數Cq,使得
|u|q≤Cq||u||,u∈H1(RN)
(4)
方程(1)對應的能量泛函是
由Hardy-Littlewood-Sobolev不等式和式(4)知,J在H1(RN)上被很好地定義,并且屬于C1。它的導數是
(▽u·▽v+uv)-
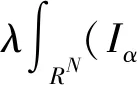
u,v∈H1(RN)
因此,方程(1)的弱解是能量泛函J的一個臨界點。下面給出著名的Hardy-Littlewood-Sobolev不等式[8]。
引理1(Hardy-Littlewood-Sobolev不等式) 若s,t>1,μ∈(0,N)滿足
則存在正常數C(N,μ,s),使得對于所有的u∈Ls(RN),v∈Lt(RN),有
為了得到泛函J的一個(PS)c序列,需要驗證J滿足山路結構。
引理2泛函J滿足山路結構,即
① 存在r,η>0,使得對于所有滿足||u||=r的u有J(u)>0,而且對于所有滿足0<||u||≤r的u有J(u)>0。
② 存在u0∈H1(RN), 使得||u0||>r和J(u0)<0成立。
證明
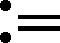
C1t2-C2t2p-C3t2*,t∈R+
所以,
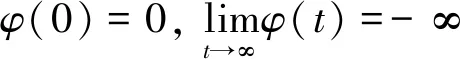
故存在t0>0且t0足夠大,使得對于u0=t0u,②成立。
通過經典的山路定理[7],能量水平c0可以刻畫為
(5)
其中:Γ={γ∈C([0,1],H1(RN);γ(0)=0,J(γ(1))<1}。
為了確保緊性,現在對能量水平c0給出一個估計。
令S是最佳Sobolev嵌入常數,即
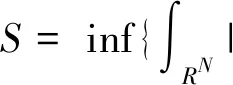
引理3設N≥3且c*=SN/2/N,則c0 證明令 對任意的u∈H1(RN){0},由引理2的②可知,存在tu>0,使得J(tuu)<0。 因此,由c0的定義可知, 于是c0≤c1。為了完成證明,下面只需證明c1≤c*。 令h(t)=J(tu0),t∈R+,則h′(tλ)=0,也就是 進一步得到 注意到,當λ→∞時,有 于是,tλ→0,λ→∞。由h的連續性可知, 因此存在λ0>0,使得對于所有的λ≥λ0,有 于是對于所有的λ≥λ0,有 在這一部分,分兩步來證明定理1,首先證明方程(1)在c0 令 引理4如果{un}是H1(RN)中的一個序列且滿足 則 證明注意到 再結合S的定義,可得 于是, (6) 因此, (7) 結合式(6)和(7)得到理想結論。 引理5設{un}?H1(RN)是J的一個(PS)c序列,則{un}在H1(RN)中是有界的。 證明取μ=min{2p, 2*}>2,由{un}?H1(RN)可知J的一個(PS)c序列: c+on(1)+on(1)||un||=J(un)- 于是,{un}在H1(RN)中是有界的。 引理6設{un}?H1(RN)是J的一個(PS)c序列,其中c∈(0,c*),則存在平移過的子序列{un}弱收斂到u≠0,而且 J′(u)=0,J(u)∈(0,c] 證明本文斷言 事實上,若不成立,則由Hardy-Littlewood-Sobolev不等式可知 *|un|p)|un|p=0 (8) 由〈J′(un),un〉=on(1)可知 *|un|p)|un|p+ (9) 結合式(8)和(9)可得 另一方面,由J(un)→c>0可以得到 于是,由引理4可知 與已知條件矛盾。因此,根據文獻[7],存在{un}的子序列,仍記為{un},σ>0和{yn}?RN,使得對所有的n, (10) 記vn(·)=un(·+yn)。由J的平移不變性可知{vn}也是J的一個(PS)c序列。通過引理5可知,{vn}在H1(RN)中是有界的, 因此可以假設在H1(RN)中{vn}弱收斂到u,而且由式(10)可知u≠0。 現在證明J′(u)=0。根據文獻[9],對任意的w∈H1(RN),有 *|vn|p)|vn|p-2vnw→ 而且 所以J′(u)=0。 取引理5中的μ,可推出 用范數的弱下半連續性和Fatou引理可得 于是J(u)∈(0,c]。 定理1的證明由引理2和山路定理可知,在H1(RN)中存在J的一個(PS)c0序列{un},即 J′(un)→0,J(un)→c0 其中能量水平c0在式(5)中給出了定義。由引理5知,當λ>λ0時,c0∈(0,c*)。因此,通過引理6知,若{un}弱收斂到u,則u是泛函J的非平凡臨界點J(u)∈(0,c0]。 下面證明由式(3)定義的極小化問題是可達的。令{vn}是由方程(1)的非平凡解構成的序列,且滿足 當λ>λ0時,觀察到m≤c0 (11) 所以{vn}在H1(RN)中是有界的。而且由Hardy-Littlewood-Sobolev不等式和式(4)可得: *|vn|p)|vn|p+ 因此, 再結合式(11)知m>0。因為序列{vn}是泛函J的一個(PS)m序列,再次用引理5,可知存在u∈H1(RN){0},使得J′(u)=0,而且J(u)∈(0,m]。另一方面,由m的定義可得J(u)≥m。因此,J(u)=m,即u是方程(1)的基態解。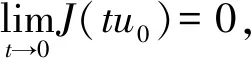
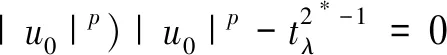
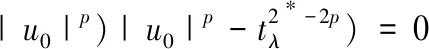
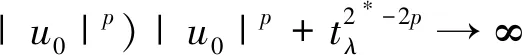
2 定理1的證明