雙場耦合破乳脫水裝置的錐段結構優化

余 保,龔海峰,戴 飛

(1.重慶理工大學 機械工程學院， 重慶 400054； 2.重慶工商大學 廢油資源化技術與裝備教育部工程研究中心， 重慶 400067)

工業廢油的資源化再利用對于緩解能源緊缺、節約資源以及環境保護等具有重要意義[1-3]。乳化液的破乳脫水處理是眾多資源化再利用工藝中的首要環節[4]。對于含水量較高、成分復雜的廢油乳化液，各種單一的工藝方法在處理成本、耗能及耗時等方面均存在局限，采用多場耦合或集成技術實現乳化液高效破乳脫水處理是未來發展的趨勢[5]。因此，提出了一種集成高壓電場和旋流離心場的耦合破乳脫水裝置[6]。該裝置以雙錐脫水型旋流器為本體結構嵌入高壓電極。在不同的應用目的、需求以及進給材料參數下，對本體結構的結構參數進行優化可有效地提高裝置的分離效率[7]。響應面法作為一種以數學統計為基礎的非線性優化方法，可用于分離裝置的多個結構參數優化[8-10]。Tang 等[11]利用中心組合設計和響應面法對旋流器溢流口結構參數進行了優化，且發現經過優化后的裝置具有更高的分離精度。Vieira等[12]利用數值計算以及響應面法對旋流器的幾何參數進行了優化，結果表明：經幾何參數優化后的裝置具有較低的歐拉數和更小的截斷尺寸。

由于耦合裝置本體結構的錐形段是非常重要的分離區域，通過優化錐形段的結構參數可以有效地改善耦合裝置的分離效率。因此，嘗試利用響應面法對耦合裝置的錐段結構進行優化。采用數值模擬方法，結合Box-Behnken因子設計和響應面法對耦合裝置的幾何參數進行優化，對設計和制造高性能的雙場耦合破乳脫水裝置具有指導意義。

1 模型與方法

1.1 模型與方程

雙場耦合破乳脫水裝置的結構模型如圖1所示。該模型主要包括直管段、大錐段、小錐段和底流管。在直管段包括一個溢流管和2個圓柱形入口，且2個圓柱形入口與直管段相切。溢流管的柱形外壁為電源的正極，直管段的柱形內壁為高壓電源的負極，在兩柱形壁面之間區域內形成高壓電場。乳化液經入口進入到該區域內，乳化液中的分散相液滴在高壓電場作用下發生快速聚結使其粒徑變大，然后在旋流作用下快速地分離。建立以底流口中心點為原點的笛卡爾坐標系，z軸沿中軸線并指向溢流口。耦合脫水裝置的主要結構參數主要包括公稱直徑D、直管段直徑DS、溢流口直徑DO、入口直徑Di、溢流管伸入長度Lo、底流管長度Lu、底流口直徑Du、小錐角α和大錐角β。在本研究中，DS、DO、Di、Lo、Lu、Du的值分別為70 mm、18 mm、12 mm、45 mm、400 mm和10 mm，且均保持不變。

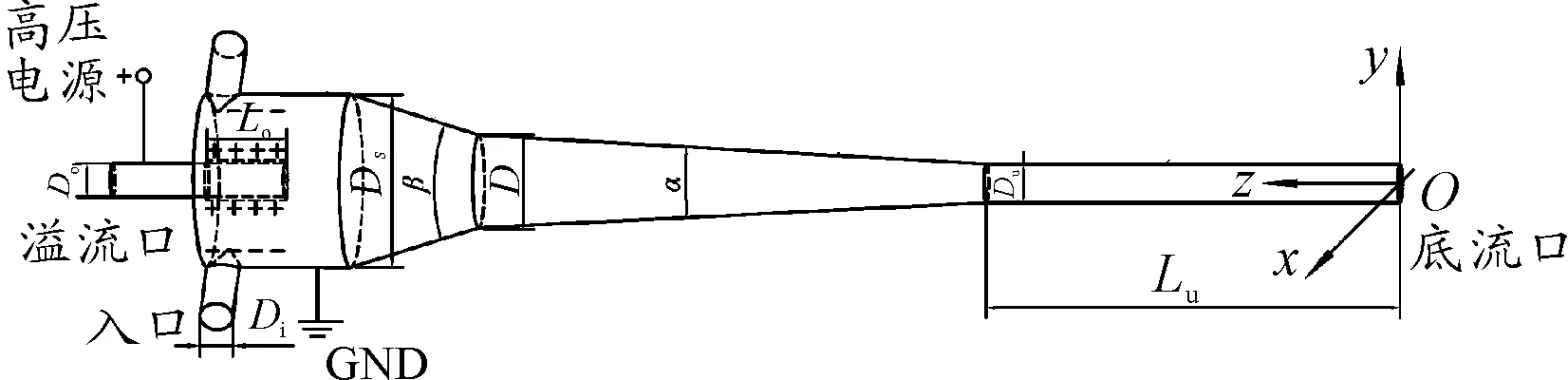
圖1 雙場耦合裝置結構模型

耦合裝置內部為復雜的湍流流動，且滿足不可壓縮流的運動條件。控制方程采用Mixture模型，用雷諾應力模型對湍流流動情況進行模擬。Mixture模型和雷諾應力模型的具體表達見文獻[13]。

由于高壓電場的存在，在耦合裝置中的分散相液滴會受到電場力。電場力可由式(1)表達。

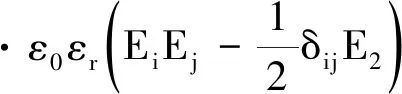
(1)

式中：ε0為真空絕對介電常數(F/m)；εr為相對介電常數；Ei，i=1,2,3表示沿著x、y、z方向電場強度(kV/m)；Ej，j=1,2,3表示沿著x、y、z方向電場強度(kV/m)；δij為克羅內克符號；E為電場幅值有效值(kV/m)。

在高壓電場區域，分散相液滴發生聚結后粒徑發生變化。根據液滴聚結模型[14]，粒徑控制方程可表達為 ：

(2)

n=[t/t1]

(3)

R′=(2n)1/3R

(4)

式(2)～(4)中：t1為液滴成對結聚時間(s)；μ為油液動力黏度(Pa·s)；φw為油中含水體積分數(%)；n為[t/t1]的整數部分；t為液滴在電場區停留時間(s)；R為聚結前液滴半徑(mm)；R′為聚結后液滴半徑(mm)。

1.2 網格劃分與邊界條件

利用ANSYS Meshing(ANSYS 15.0)對耦合裝置模型進行網格劃分。采用自動劃分的方式進行非結構網格劃分。為確定網格的獨立性，初始網格數量為248 967，在相同邊界條件下，將網格數量增大到342 128，計算后得到直管段內最大切向速度的改變量超過5%，再增大網格數量到422 987時，最大切向速度值的改變量不超過5%。因此，考慮到預測精度以及計算花費，網格數量為342 128可以滿足數值計算要求。

設圓柱形入口為速度入口，且其法向速度為10 m/s，軸向和徑向速度為0。入口處的湍流強度為5%，水力直徑為12 mm。設耦合模型的溢流口和底流口為自由出流，且分流比分別為0.9和0.1。其他壁面為無滑移邊界條件。在靠近壁面區域采用標準壁面函數。高壓電場電壓幅值為11 kV。

1.3 物性參數與求解器設置

乳化液中連續相為油，分散相為水。油的含水量為10%，其分散相水滴平均粒徑為200 μm。為了確保乳化液在耦合裝置中能有較好的分離效果，對油液進行加熱，溫度設定為70 ℃。在該溫度下，油相的密度為863 kg/m3，黏度為16.807 mPa·s；水相的密度為998.3 kg/m3，黏度為1.3 mPa·s。

采用CFD軟件ANSYS Fluent(ANSYS 15.0)對不同結構參數下的耦合裝置數值模型進行計算。將用戶自定義函數方法用于定義高壓電場方程以及粒徑控制方程，以實現電場與流場的耦合模擬計算[15]。采用有限體積法對三維、不可壓縮流動的Navier-Stokes方程進行離散。semi-implicit method for pressure linked equations consistent(SIMPLE)代碼用于耦合連續性方程以及動量方程中的壓力與速度求解。quadratic upstream interpolation for convective kinetics(QUICK)格式用于動量方程、體積分數方程、雷諾應力方程、湍動能以及湍流耗散率方程的離散。PREssure staggered option (PRESTO)格式用于壓力插值。所有的數值模型均采用瞬態模擬，且時間步長為0.05 s。

2 結果與分析

2.1 參數設計及計算結果

設大錐角、小錐角和公稱直徑的取值范圍分別為：20° ～ 22°、5° ～ 6°和20 ～22 mm。利用Box-Behnken試驗設計原理，對3個因素(大錐角、小錐角和公稱直徑)及其水平進行響應面設計，優化耦合脫水裝置錐段尺寸。以裝置溢流口脫水率和底流口脫油率為響應值，自變量為小錐角(°)、大錐角(°)和公稱直徑(mm)。各因子編碼及自變量水平如表1所示。利用Design-Expert 軟件按表1中的因子編碼及自變量水平進行試驗設計，同時利用數值方法得出各試驗條件下的響應值，其結果如表2所示。

表1 試驗因子水平及編碼

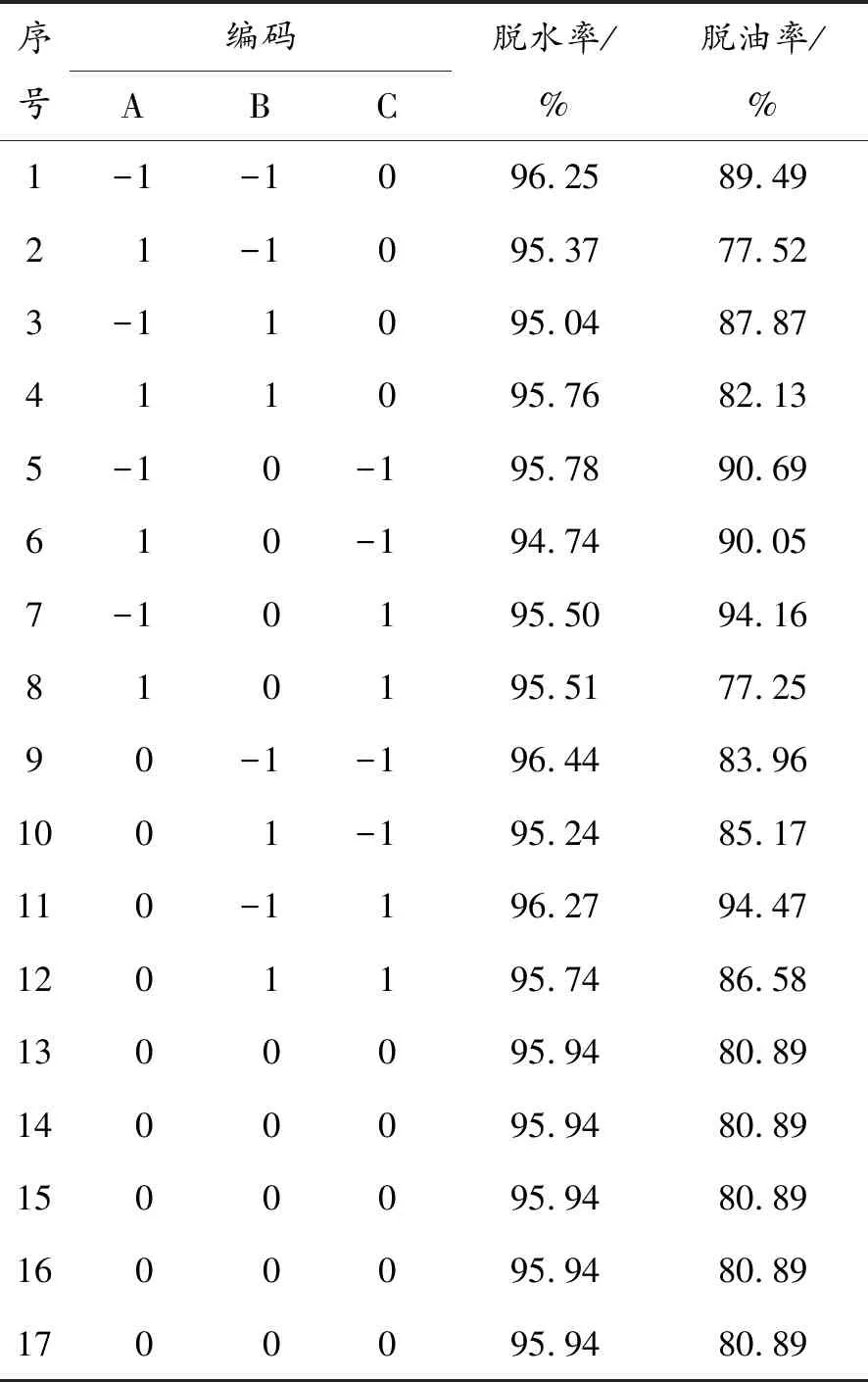
表2 Box-Behnken試驗設計方案及結果

2.2 響應模型與方差分析

采用Design-Expert 8.0軟件對表2中的數據進行響應面分析，建立多元二次回歸模型：

Edw=266.26-8.798x1-12.43x2-1.197x3+

0.799x1x2+0.528x1x3+0.166x2x3-

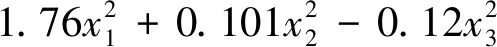
(5)

Edo=1716.68+11.68x1-29.9x2-126.5x3+

3.11x1x2-8.13x1x3-2.28x2x3+

(6)

式中：x1、x2和x3分別對應α、β和D；Edw為脫水率(%)；Edo為脫油率(%)。

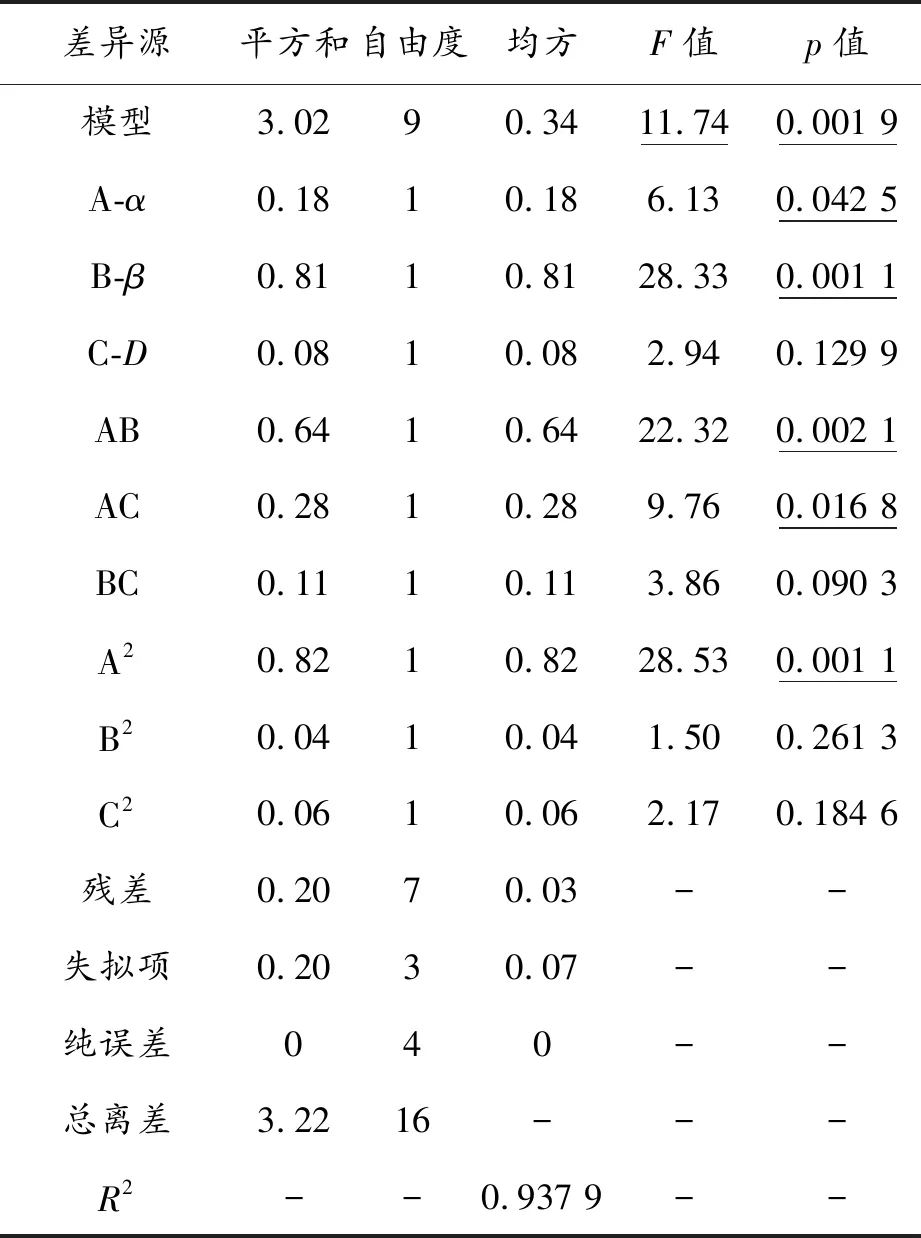
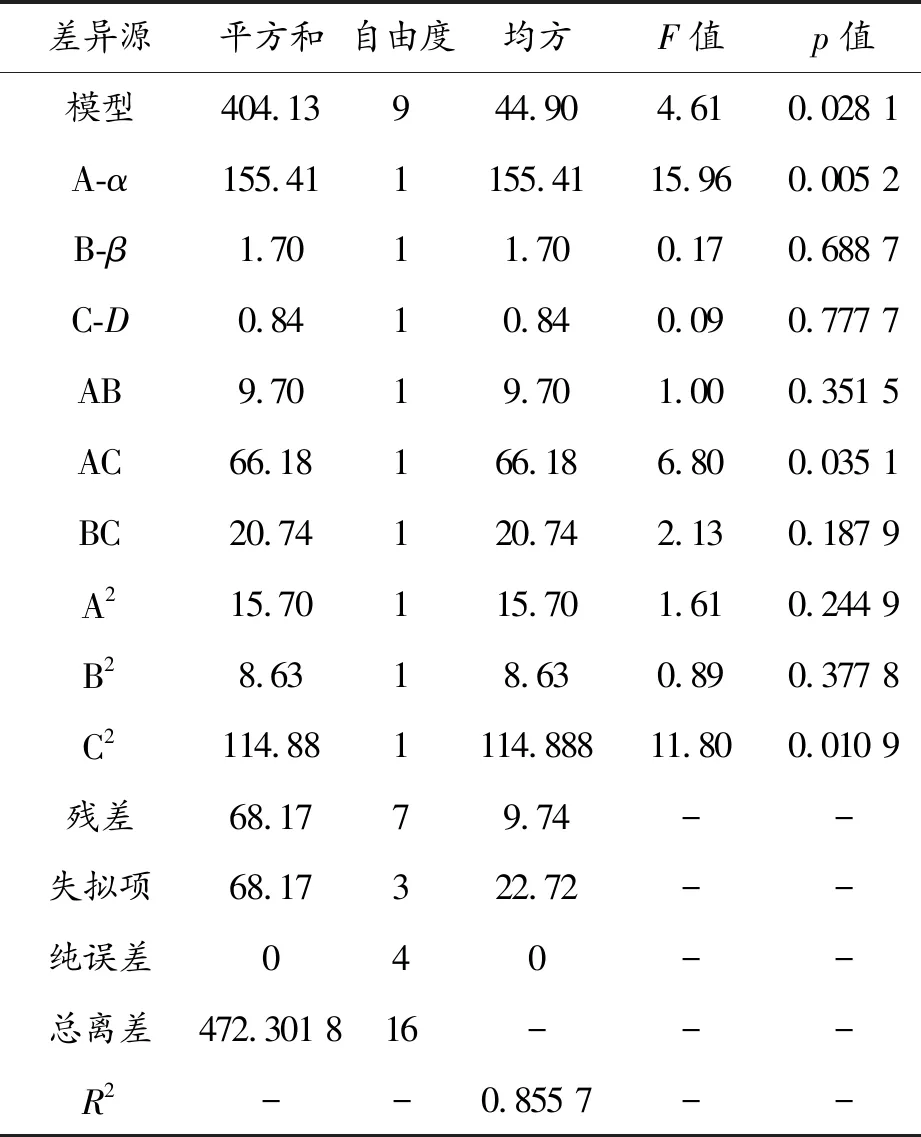
二次回歸模型的方差分析結果如表3和表4所示。從表3、4中可以看出：模型的F-value分別為11.74和4.61，與其對應的p-value分別為0.19%和2.81%，均小于5%，即式(5)和式(6)表示的響應模型是顯著的。其中，脫水率響應模型中的顯著項有A、B、AB、AC和A2；脫油率響應模型中的顯著項有A、AC和C2。此外，兩響應模型的復相關系數值R2分別為0.937 9和0.855 7，表明模型均具有較高的顯著性。

表3 脫水率的模型方差分析結果

差異源平方和自由度均方F值p值模型3.0290.3411.740.001 9A-α0.1810.186.130.042 5B-β0.8110.8128.330.001 1C-D0.0810.082.940.129 9AB0.6410.6422.320.002 1AC0.2810.289.760.016 8BC0.1110.113.860.090 3A20.8210.8228.530.001 1B20.0410.041.500.261 3C20.0610.062.170.184 6殘差0.2070.03--失擬項0.2030.07--純誤差040--總離差3.2216---R2--0.937 9--

耦合脫水裝置脫水率和脫油率的可信度分析結果如圖2所示。從圖2可以看出：預測值與實際值接近，表明響應模型與數值計算擬合度較好。

為進一步研究各因素間的交互作用對分離效率的影響，本文對二次回歸模型進行響應面分析，得到的響應立體分析結果和等高線圖如圖3、4所示。從圖3中可以看出：同時減少小錐角α和大錐角β可較小程度地提高裝置溢流口脫水率，且當小錐角為5°時，大錐角從22°減小到20°，脫水率從95.03%增大到96.24%。圖4中可見：同時增大公稱直徑D和減少小錐角α可以明顯地提高底流口脫油率，且當小錐角為5°時，公稱直徑D從20 mm增大到22 mm，脫油率從90.69%增大到94.16%。

表4 脫油率的模型方差分析結果

差異源平方和自由度均方F值p值模型404.13944.904.610.028 1A-α155.411155.4115.960.005 2B-β1.7011.700.170.688 7C-D0.8410.840.090.777 7AB9.7019.701.000.351 5AC66.18166.186.800.035 1BC20.74120.742.130.187 9A215.70115.701.610.244 9B28.6318.630.890.377 8C2114.881114.88811.800.010 9殘差68.1779.74--失擬項68.17322.72--純誤差040--總離差472.301 816---R2--0.855 7--

2.3 最佳結構參數

以裝置的脫水率和脫油率達到最大值為最優條件，通過對響應模型進行求解分析得到優化結果；同時，為驗證響應曲面模型求解的合理性，在最佳分離效率條件下采用數值計算方法對裝置模型進行模擬計算，得到的結果如表5所示。表5中：S表示模擬計算值；P表示模型預測值。由表5可知：響應模型的預測值與數值計算值相差較小，其中：脫水率響應模型的最大偏差約為0.24%，脫油率響應模型的最大偏差為3.46%。因此，響應模型的最優解是合理的。

表5 優化條件下模擬值與預測值

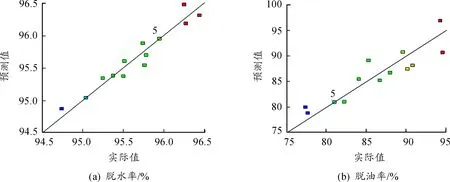
圖2 預期值與實際值對比曲線

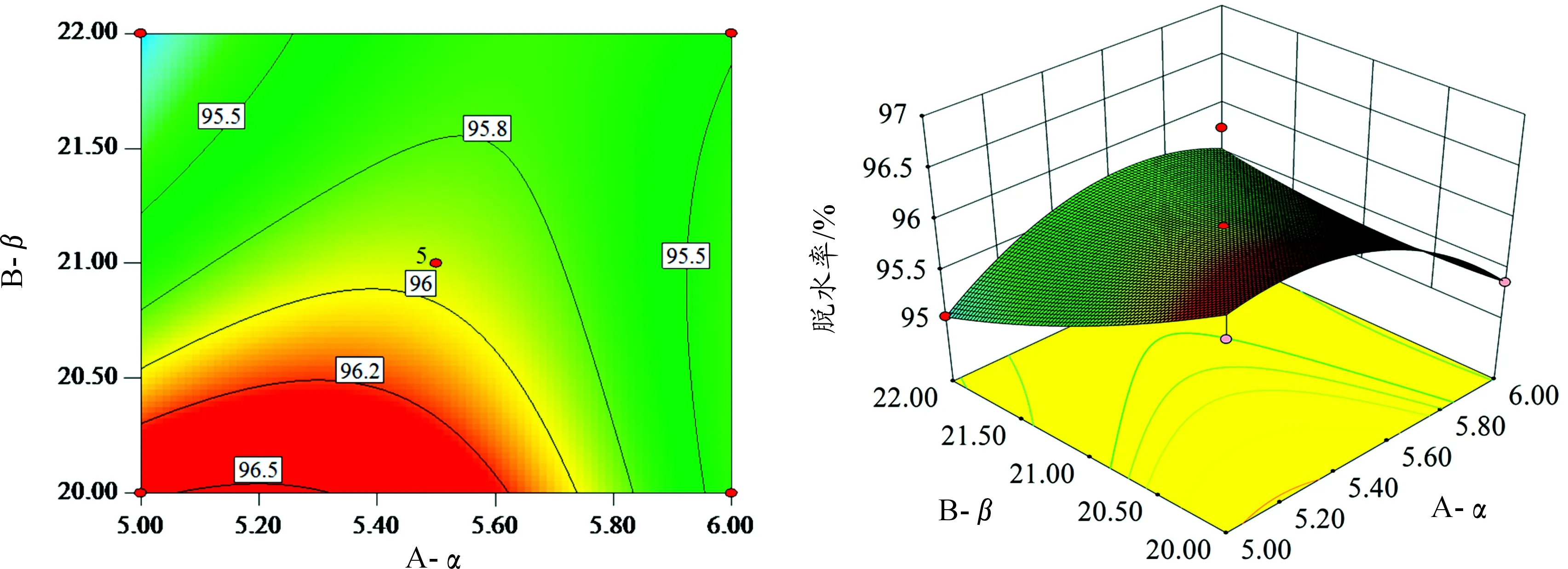
圖3 α-β間的交互作用對脫水率的影響

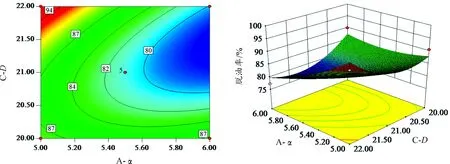
圖4 α-D間的交互作用對脫油率的影響

3 結論

針對雙場耦合破乳脫水裝置用Design Expert 8.0軟件建立響應模型對其錐段結構進行優化。

1) 利用數值模擬，結合使用Box-Behnken因子設計和響應面法，建立了各結構參數與分離效率間的擬合回歸模型。小錐角與大錐角之間的交互作用對裝置溢流口脫水率的影響顯著；小錐角與公稱直徑之間的交互作用對裝置底流口脫油率的影響顯著。

2) 根據響應模型計算結果，得到最佳結構參數為：小錐角、大錐角和公稱直徑的最佳取值分別為5.09°、20°和22 mm，且在該條件下耦合裝置的脫水率和脫油率的數值計算值分別為96.46%和97.05%。