梯次利用鋰離子電池健康狀態估計

(北京信息科技大學、北京電動車輛協同創新中心 北京 100192)

通常來講，動力電池的平均使用年限大約為5-8年，其性能隨著使用時間的增長而逐漸衰退，當電池的當前容量衰減至額定容量的80%是，將不再適用于電動汽車，必須從原來的電動車退役。而這些退役電池的容量大多數在初始容量的60%-80%，如果直接報廢，將造成資源的巨大浪費。根據預測，到2020年我國新能源汽車退役動力電池累計將達25GWh。如此規模的退役動力電池，如果不能妥善處置，勢必將對生態環境造成新一輪的污染，也將影響到我國新能源汽車及動力電池產業的健康發展。因此，開展電池梯次利用，有利于資源的合理利用，這就涉及到退役電池的篩選，準確的估計退役電池的健康狀態是電池篩選的必要步驟。

采用了Thevenin等效電路模型，基于HPPC實驗對該等效電路模型進行了參數辨識，并通過Matlab-simulink建立了電池的等效電路模型并進行了模型的驗證。進行電池的SOH估計之前，首先采用拓展卡爾曼濾波對電池的SOC進行估計，接下來采用雙拓展卡爾曼濾波對電池的SOC和SOH進行同時估計并通過仿真對該算法進行了驗證。

一、電池模型的建立

(一)電池模型的選擇

Thevenin等效電路模型如圖所示，鋰電池的開路電壓等效為Uoc，Ro為鋰電池的歐姆內阻。Rs表示電池的極化內阻，Cs表示的是電池的極化電容，他們組成電池的一階RC并聯回路，以此來代表電池在極化過程中的壓降[1]。

圖1 戴維南等效電路模型

(二)電池等效電路模型的建立

首先，利用Matlab的Simulink模塊搭建電池的等效電路模型。圖2是電池的Simulink等效電路模型。

圖2 電池等效電路模型

(三)模型的參數辨識

針對戴維南模型，Ro,Rs,Cs等參數未知，可以通過實驗進行識別。對于此，采用HPPC實驗法進行參數的識別。HPPC(混合脈沖功率特性試驗，Hybrid Pulse Power Characteristic)采用脈沖電流來測試電池的動態功率特性。對于等效電路模型的相關參數，可利用HPPC的實驗結果進行識別[2]。室溫下進行HPPC實驗，如下：

1.實驗設備。實驗對象為8塊錳酸鋰退役電池,以及電池充放電測試設備。

2.實驗前的預處理，首先對電池進行預處理循環：①以0.2C恒流充電至截止電壓4.3V，接下來進行恒壓充電至電流為0.02C為止。②靜置1小時。③以0.2C放電至放電截止電壓3V。④靜置1小時。⑤重復步驟①-④五次。⑥以最后三次所測得電池容量的平均值為電池的實際容量。

3.根據FreedomCar混合動力汽車電池測試手冊中的HPPC實驗，實驗步驟。如下：①測試前，以0.2C的電流恒流將電池充至充電截止電壓4.3V，接下來以恒壓充至電流減小至0.02C為止；此時電池充滿，此過程即為CCCV的充電過程。②擱置1小時，使電池處于平衡狀態。③用1C電流放電10s，擱置40s后再用0.75C的電流充電10s，用1C電流是SOC減少10%，靜置1小時。④重復步驟③,當SOC=10%時停止實驗[3]。

HPPC實驗的全程電流示意圖如圖3所示。

4.節點的參數識別。結合電池戴維南模型原理以及電池放電過程中的電壓特性可對每個節點參數進行識別。首先選取節點為SOC=90%的電流和電壓示意圖，如圖4所示。

通過觀察圖4可以總結得到，整個HPPC實驗包括兩個階段，充電和放電。兩個階段較為相似。所以在此僅研究U1至U5的放電階段。也就是研究U1-U2,U2-U3,U3-U4,U4-U5。

式中τ=TpCs為時間常數

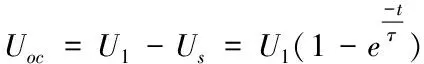
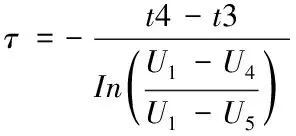
到此，該節點的參數識別完畢；其他節點的參數識別同理可得[5]。依據HPPC實驗數據可計算得到各項參數。

二、模型的驗證

接下來進行模型的驗證，通過對比模型的計算電壓以及實際測量所得的電壓，來驗證模型的精確度。模擬HPPC實驗的一段，將得到的仿真數據和實驗所得的數據進行對比。

圖5 數據對比圖

從圖5中可以看出，模型測量值與實際測量值圖像的走勢大致相同。模型測量值和實際測量值絕對誤差不超過40mv，因此，戴維南等效電路模型準確度滿足要求。可以看出，戴維南模型可以滿足模擬電池工作的要求。而且，通過實驗辨識的參數可信度滿足要求[4]。

三、雙拓展卡爾曼濾波估計電池的健康狀態

(一)基于拓展卡爾曼濾波的電池的SOC估計

由電池的等效模型的狀態方程可得，要準確估計電池的SOH，其前提是準確的估計電池的SOC。因為電池的SOC屬于非線性變化，所以在此采用EKF(拓展卡爾曼濾波)對電池的SOC進行估計。下式為系統的狀態方程以及測量方程[5]：yk=g(xk,uk)+vky(k+1)=f(xk,uk)+wk

依據戴維娜等效電路模型得出的電池SOC的估計的矩陣方程是：

f=(xk,uk)=Ak-1xk-1+Bk-1uk-1

g(xk,uk)=Uoc,k+Ub(k)+i(k)Ra(k)

(二)基于雙拓展卡爾曼濾波的電池的SOH的估計

圖6 雙拓展卡爾曼濾波工作原理

圖6為雙拓展卡爾曼濾波的工作原理，所謂雙擴展卡爾曼濾波實際上就是兩個拓展卡爾曼濾波同時工作(即EKF1和EKF2)。這之中，EKF1進行狀態估計，EKF2進行參數估計。在這兩個濾波器之中都具有狀態更新以及量測新。

在本節，采用雙拓展卡爾曼濾波，電池健康狀態及荷電狀態被同時估計。估計SOC的拓展卡爾曼濾波器是電池的參數估計。剩下的一個濾波器被用來估計電池當前時間的額定容量。最后，利用電池的容量的定義公式來計算電池當前時間的健康狀態[6]。

本節采用的DEKF詳細的過程在此列出：

首先，電池當前時間的實際可用容量，在此假設為一個緩變參數，依據前文電池健康狀態(SOH)和荷電狀態(SOC)估計過程之中建立的方程，并且在本文建立的等效電路模型的基礎之上，可以得到以下的雙拓展卡爾曼濾波的估計模型：

xk+1=akxk+Bkuk+wkCk+1=Ck+rk

yk=Uoc,k+Ub(k)+i(k)×Ra(k)+vk=g(xk,uk)+vk

依據上式知道，雙拓展卡爾曼濾波的基礎上，電池健康狀態(SOH)的估計是和電池荷電狀態(SOC)的估計是同時進行的。即在估計電池的SOC同時，也估計了一次電池的當前時間實際最大可用容量。

DEKF的具體過程是：

1.當K=0時，進行初始化

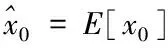
2.時間更新過程

3.測量更新過程

(三)算法的驗證與分析

以上是基于雙拓展卡爾曼濾波算法進行估計得到SOH,為了驗證其準確性，接下來進行仿真，以此來分析對比。在仿真的過程中首先設置電流激勵曲線，該曲線應在0.3C、0.4C、0.5C三種電流倍率之中隨機生成，以此來對應驗證前文進行的退役電池所進行的容量測試實驗。在此設置電池的初始容量為30.56Ah，SOC的值是95%，仿真所進行的時間是1200s.圖7為仿真所得到估計曲線和實驗所得到的真實測量值曲線的對比。

圖7 拓展卡爾曼濾波估計值與容量真實值對比

在圖7中可以看出，在仿真進行的初始時段，估計值和測量值存在一些偏差。但是在經歷了一段時間的波動之后，拓展卡爾曼濾波算法的估計值較迅速的收斂于真實的容量值附近。并且隨著時間的增加，由于卡爾曼增益的作用，使得仿真誤差越來越小并且逐漸維持在較小的誤差范圍之內。仿真對比結果表明，雙拓展卡爾曼濾波算法具有很好的優勢，精度高，具有很好的魯棒性。

四、總結

本章首先對幾種常見的電池模型進行了分析，綜合各自的優缺點，最終采用了計算簡單，準確度較高的戴維南等效電路模型。在選擇好電池模型之后，進行了等效電路模型的參數辨識，基于HPPC實驗，對該電路的參數盡行了辨識。隨后進行了參數的驗證實驗。接下來簡單介紹了卡爾曼濾波以及拓展卡爾曼濾波，在此基礎上建立了SOC和SOH的估計模型。最后采用DEKF算法估計了電池的SOH。并進行了仿真實驗，以此來驗證算法以及模型的準確度。