考慮邊界滑移的微通道熱沉傳熱傳質性能研究

宋世宇，何 磊，景大雷

（上海理工大學 機械工程學院，上海 200093）

隨著系統微型化、集成化水平的迅猛發展，微尺度器件在微電子工程、微生物工程、航空航天等領域的應用越來越廣泛，這對系統的散熱性能提出了更高的要求[1]。目前超高性能CPU芯片的發熱量可達106W/m2的數量級，與之相伴的由溫度引起的元器件失效率隨著溫度的升高呈指數式上升。研究表明：在規定的器件工作溫度范圍之內，電子元器件的溫度降低1 ℃，其故障發生的概率可以減少4%左右；如果超過最大規定溫度值10～20 ℃，則故障發生的概率就會提高100%[2]。因此，全新的微電子器件散熱技術成為當今研究的熱點問題之一[3]。

20世紀80年代初，Tuckerman等[4]首先提出了微通道散熱技術的構想，通過在硅片上刻蝕流道的方法加工出微通道散熱器，并將其運用于電子設備的水冷散熱，取得顯著效果。實驗發現，當水以強制對流的方式通過該微通道換熱器時，最高可以帶走790 W/cm2的熱流量。自從這一標志性論文發表之后，微通道散熱器傳熱傳質性能得到深入研究，并廣泛地應用于諸多微電子設備散熱問題的解決[5-8]。

在研究微通道熱沉的傳熱傳質性能時，合理地確定微通道固液接觸面上的速度邊界條件是必須要解決的問題之一。雖然前人就微通道熱沉的截面形狀和尺寸對于流體阻力及散熱性能的影響進行了大量的研究[9-11]，但是，大多數研究考慮的是無邊界滑移條件，即在微通道固液接觸面上沒有相對運動速度。然而，在微納尺度下的流體流動，無邊界滑移并不完全適用。已有的研究發現，邊界滑移確實存在于微尺度下的流體流動中[12-13]。相對應于無邊界滑移，邊界滑移是指在固液接觸面上流體分子與固體表面之間有相對運動速度的存在。為表征邊界滑移的程度，Navier[14]提出了線性滑移邊界條件假設，給出了滑移長度的概念，用于表征邊界滑移的程度[14-16]。已有研究發現，滑移長度的范圍可在幾納米到幾十微米之間[17]，這會對微通道流體的傳熱傳質性能產生顯著的影響。

為了解決上述問題，本文選用具有矩形、橢圓形和三角形這3種不同截面形狀的微通道熱沉，研究了邊界滑移對微通道熱沉傳熱傳質的影響，以及微通道熱沉傳熱傳質性能的截面形狀和截面尺寸依賴性問題。

1 微通道仿真模型的建立

微通道散熱主要是通過流體與熱源進行熱量的交換傳遞，由流體將熱量帶走。為研究微通道熱沉傳熱傳質性能的截面形狀依賴性，本文建立了具有3種不同截面形狀的微通道熱沉模型，截面形狀分別為矩形、橢圓和等腰三角形，具體結構如圖1所示。同時，在保證截面橫截面積不變的條件下，通過調整橢圓截面的長短軸之比、矩形截面的高寬之比和等腰三角形截面的頂角及腰長的方式來調整截面的尺寸，研究微通道熱沉傳熱傳質性能的尺寸依賴性。考慮微通道熱沉整體結構的對稱性，本文僅選用具有單根管道的區域進行仿真，仿真區域如圖1中虛線框所示，3種截面形狀的截面面積均為225π μm2，仿真區域通道長度 L為 1 000 μm，寬 W和高 H均為 200 μm。a和b分別表示橢圓截面的長軸和短軸，t和w分別表示矩形截面的高和寬，l和θ分別表示等腰三角形截面的腰長和頂角。

假設微通道中的流體為不可壓縮牛頓流體且在層流的狀態下流動，同時，假定流體處于穩定流狀態且忽略重力等體積力的影響。此時，流體的流動狀態應滿足連續介質理論，并由以下控制方程[18]來描述：

式中：v為流體流動的速度；ρ為流體的密度；p為壓力；η為流體的動力黏度。

此外，假定熱量傳遞處于熱穩定的狀態，熱量在微通道熱沉中穩定傳遞的控制方程為[18]：

流體區域

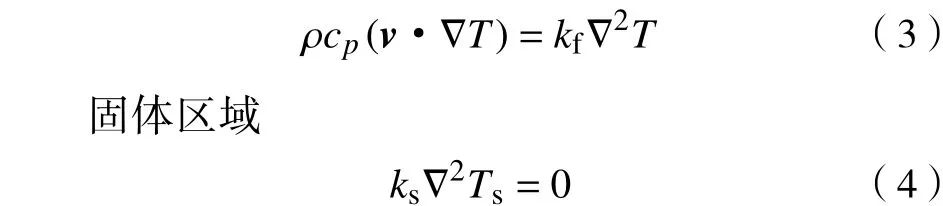
式中：cp為流體的比定壓熱容；kf為流體的導熱系數；T為流體溫度；ks為散熱器固體導熱系數；Ts為散熱器固體溫度。

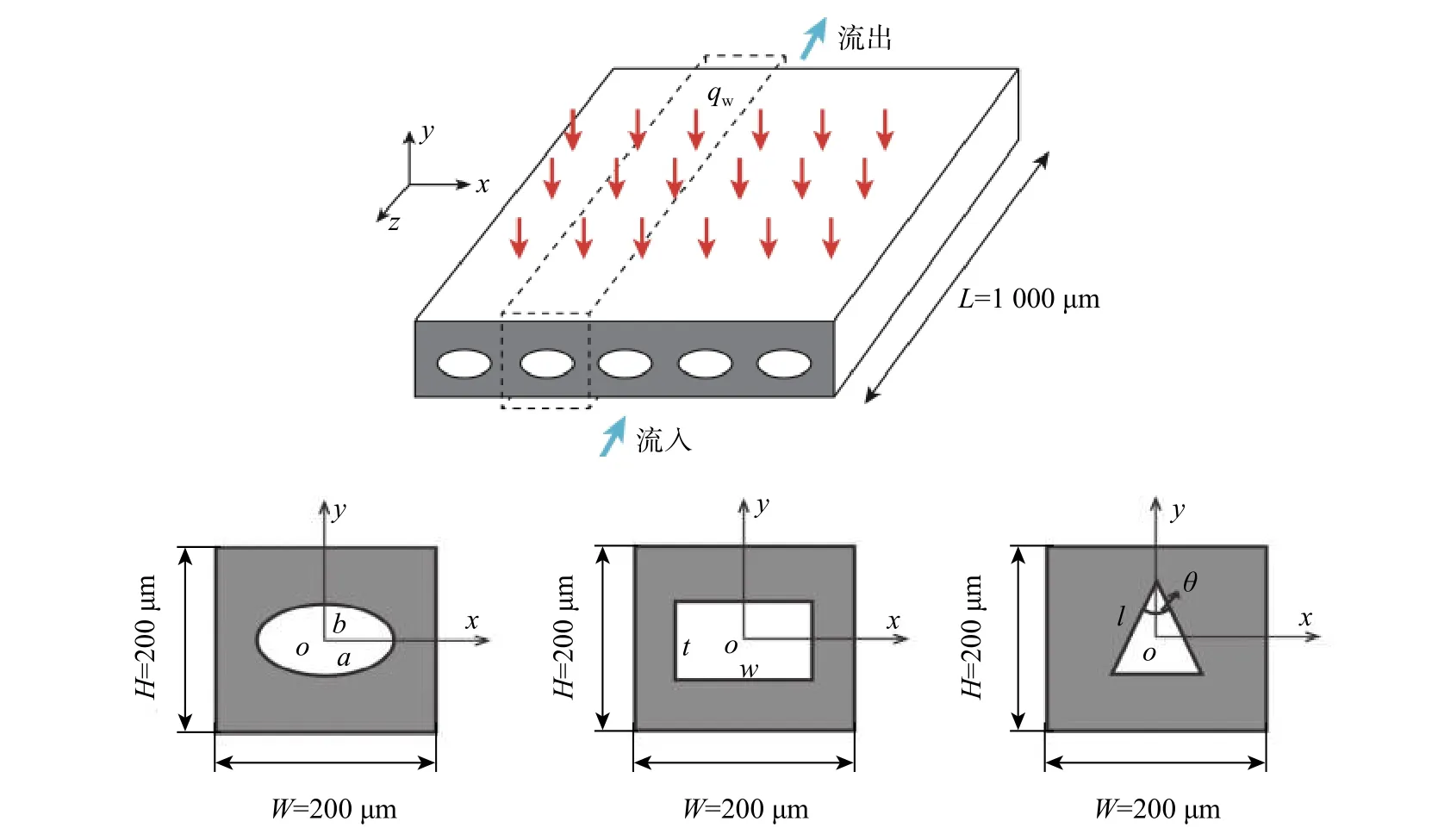
圖1 微通道熱沉仿真模型Fig.1 Simulation models for microchannel heat sinks

流體流動及傳熱的初始條件及邊界條件為

式中：vin，Tin分別為進口速度與進口溫度；pout為流體的出口壓力；vfw為固液接觸面的相對運動速度；為垂直于管道方向的流體速度梯度；n為垂直于管道壁的局部坐標；vf為液體運動速度；ls為固液界面上的滑移長度。

實際研究通過Comsol軟件仿真實現，選用水為冷卻液體，微通道熱沉的材料為硅。微通道熱沉的上表面有105W/m2的熱流量，熱沉其他幾個面為熱絕緣邊界，入口處水的速度為5 m/s，溫度為293.15 K，固體的導熱系數ks=130 W/（m·K），水的導熱系數 kf=0.6 W/（m·K），水的密度 ρ=996.6 kg/m3，水的比定壓熱容 cp=4 178 J/（kg·K），水的動力黏度η=0.001 Pa·s，且忽略溫度變化對水的物性參數的影響。為了研究滑移的影響，假定固液接觸面上具有不同的滑移長度（0～1 000 nm），對此進行仿真分析。

此外，引入流體阻力R及傳熱系數h這2個參數來分析微通道熱沉的傳熱傳質性能。根據泊肅葉定律可知，流體在水平通道中作無滑移層流運動時，其體積流量Q與管道兩端的壓差Δp，管的水力半徑r，長度L，以及流體的動力黏度η的關系為[19]

令 R=Δp/Q =8ηL/(πr4)，R 即為圓管流體阻力的計算公式。Comsol仿真研究的R可由式（6）直接計算得出。

其中，Δp，Q由Comsol仿真結果得出。

當有邊界滑移存在時，流體阻力可表示為[20]

泊肅葉定律是建立在流體在水平圓管中作層流運動時，當流體在任意截面形狀的微通道中作層流運動時，通道的水力半徑可通過式r=2A/P得出，A為微通道截面面積，P為截面周長。

根據牛頓冷卻定律可知，流體與固體壁面之間的對流傳熱的熱流量與它們之間的溫度差成正比，可以表示為

式中；Qh為單位時間內面積Asl（微通道中固液接觸面積）上傳熱的熱流量；Tb表示微通道壁面溫度；Tw表示微通道中水的平均溫度。

Qh可以表示為

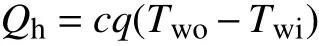
式中：c表示流體的比熱容；q為質量流量；Twi表示微通道入口處水的溫度；Two表示微通道出口處水的溫度。

2 結果與討論

2.1 仿真模型有效性分析

在Comsol仿真分析過程中，為保證模型的正確性以及網格劃分的準確性，需要對仿真模型進行驗證及網格靈敏性分析。采用的具體分析方法是以截面半徑為15 μm，通道長度為1 000 μm的圓形微通道為例，通過調整網格尺寸，將Comsol仿真得到的具有不同邊界滑移長度的微圓管流阻與式（7）的理論模型進行比較。當Comsol仿真結果與理論模型的誤差足夠小時，說明模型網格劃分合理，仿真模型是正確的。分析發現，當采用自由四面體網格，且網格數量為2.73×105時，可以得到較為準確的仿真結果。如圖2所示，仿真分析與理論結果之間的最大誤差僅為2.5%（滑移長度為1 μm時），圖中R0為無滑移時的流體阻力，ls為滑移長度。類似地，每一組模型都采用相同的方法進行了有效性分析，保證網格劃分是合理的。

2.2 滑移長度對流體阻力和傳熱系數的影響

為了分析邊界滑移對流體阻力的影響，圖3給出了邊界滑移條件對3組不同截面形狀微通道熱沉內的流體阻力影響的分析結果。R01表示截面尺寸為26.6 μm×26.6 μm的矩形微通道熱沉無滑移時的流體阻力，R02表示截面尺寸為 15 μm×15 μm的圓形微通道熱沉無滑移時的流體阻力，R03表示截面尺寸為 40.4 μm×60 ° 的三角形微通道熱沉無滑移時的流體阻力。圖3結果表明，邊界滑移的存在減弱了流體阻力，并且隨著滑移長度的增加，流體阻力逐漸減小。這與式（7）給出的流體阻力的理論結果一致。其原因是由于邊界滑移的存在影響了微通道流體的流動速度，流體流動速度隨邊界滑移的增大而增加。所以，在相同的驅動壓力下，邊界滑移增強了流體的流動，導致了體積流量的增加，意味著流體阻力的減小。

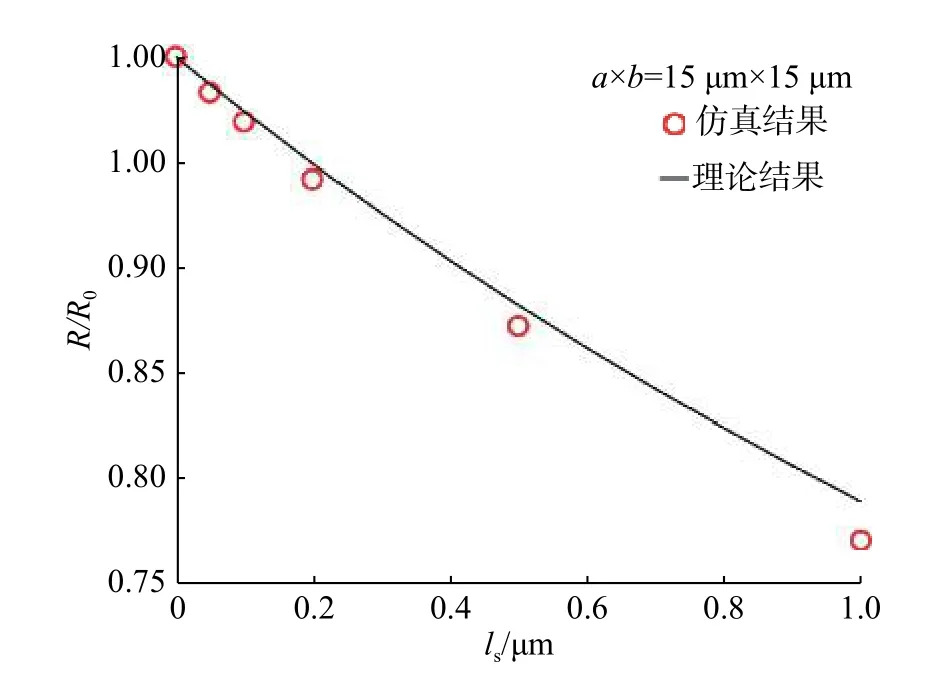
圖2 理論分析與仿真分析結果對比Fig.2 Comparison between the results of theoretical analysis and simulation analysis

圖3 滑移長度對矩形、橢圓形和三角形微通道流體阻力的影響Fig.3 Effect of slip length on the fluid resistance in rectangular, triangular and elliptical microchannels

圖4 給出了在相同的截面面積條件下，具有不同截面形狀及尺寸的微通道熱沉中邊界滑移對傳熱系數影響的結果，h01表示截面尺寸為26.6 μm×26.6 μm的矩形微通道熱沉無滑移時傳熱系數，h02表示截面尺寸為15 μm×15 μm的圓形微通道熱沉無滑移時傳熱系數，h03表示截面尺寸為40.4 μm×60 ° 的三角形微通道熱沉無滑移時傳熱系數。由圖4可以看出，邊界滑移可以有效地提高微通道熱沉的對流換熱性能，而且傳熱系數隨著滑移長度的增加而增加。這是因為在相同的驅動壓力下，邊界滑移導致流體流速的增加，從而導致體積流量的增加，單位時間內微通道中流過更多的流體，帶走更多的熱量，導致散熱能力的增強以及傳熱系數的增加。

圖4 滑移長度對矩形、橢圓形和三角形微通道傳熱系數的影響Fig.4 Effect of slip length on the heat transfer coefficient of rectangular, elliptical and triangular microchannels

2.3 截面尺寸對流體阻力及傳熱系數的影響

為了研究截面尺寸對流體阻力的影響，圖5給出了在相同截面面積下，具有不同截面形狀的微通道熱沉截面尺寸對流體阻力影響的結果。由圖5可知，在固液界面上具有相同滑移長度的條件下，矩形微通道熱沉內的流體阻力隨著矩形截面高寬比值（t/w）的增加呈現先減后增的趨勢；當矩形截面高寬比為1，即截面為正方形時，微通道熱沉具有最小的流體阻力。對于橢圓形微通道熱沉，流體阻力隨著橢圓截面2個半軸比值（a/b）的增加，呈現先減后增的趨勢；當橢圓截面2個半軸比值（a/b）為1，即截面為圓形時，微通道熱沉具有最小的流體阻力。對等腰三角形截面，隨著頂角由15 ° 增至135 °，流體阻力先減后增；當頂角為60 °，即截面為等邊三角形時，微通道熱沉具有最小的流體阻力。圖5中的結果可以根據式（7）中水力直徑對流體阻力的影響進行解釋。已知隨著水力直徑D的增加，流體阻力逐漸減小。對于圖5中的結果，隨著矩形高寬比（t/w）和橢圓2個半軸比值（a/b）的增加，微通道的水力直徑先增后減；當t/w=1或a/b=1時，相應的微通道水力直徑最大。而隨著等腰三角形頂角向60 ° 靠近，三角形截面的水力直徑逐漸增大，當頂角為60 ° 時，三角形截面的水力直徑最大。由式（7）可知，隨著水力直徑的增加，流體阻力逐漸減小，進而得到圖5所示的結果。

圖6給出了相同截面面積條件下，具有不同截面形狀的微通道熱沉截面尺寸對對流傳熱系數影響的結果。圖6的結果表明，在相同滑移長度下，傳熱系數隨著矩形高寬比的增加而先減后增；當矩形高寬比為1時，傳熱系數最小，即微通道熱沉具有最差的散熱能力。類似地，當橢圓形2個半軸之比（a/b）為1時，傳熱系數達到最小，并且傳熱系數隨著橢圓長短軸比值的增加而增加。對等腰三角形截面，當頂角為60 °，即為等邊三角形時，傳熱系數最低，散熱能力最弱；當頂角從15 °增加到135 ° 過程中，傳熱系數先減后增。上述結果也可由微通道水力直徑的變化來解釋。相同的截面面積下，具有較小水力直徑的微通道熱沉有著較大的固液接觸面積，有助于傳遞給流體更多的熱量，并由流體帶走，故具有較大的對流傳熱系數。

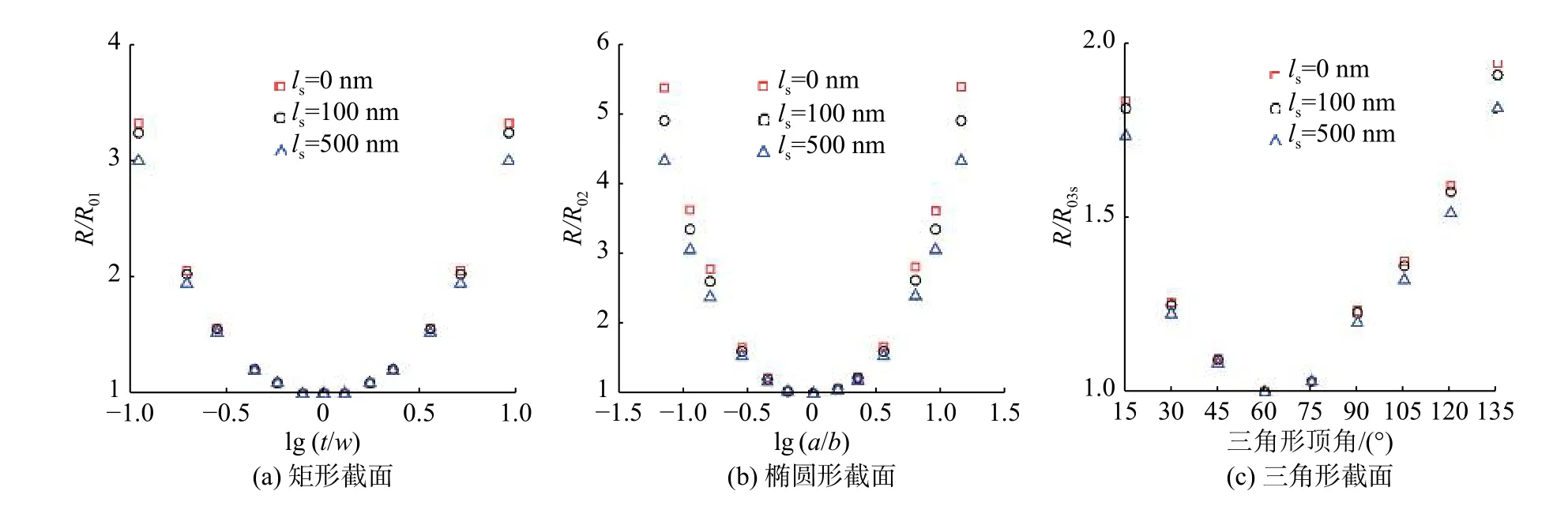
圖5 截面尺寸對矩形、橢圓形和三角形微通道流體阻力的影響Fig.5 Effect of cross-sectional dimensions on the fluid resistance in rectangular, elliptical and triangular microchannels

2.4 截面形狀對傳熱系數的影響

圖7 給出了不同截面形狀對微通道熱沉散熱性能影響的結果。圖7表明，3種截面形狀的微通道熱沉的散熱性能都是隨著水力直徑的增加而減弱，這與圖6所示的結果一致。同時，三角形微通道熱沉的散熱性能在這三者中是最差的。對于矩形和橢圓形微通道熱沉，當水力直徑小于某一臨界值時，矩形截面微通道熱沉的散熱性能優于橢圓形微通道熱沉，但當水力直徑大于這一臨界值時，橢圓形微通道熱沉的散熱效果好于矩形微通道熱沉。

圖6 截面尺寸對矩形、橢圓形和三角形微通道傳熱系數的影響Fig.6 Effect of cross-sectional dimensions on the heat transfer coefficients of rectangular, elliptical and triangular microchannels

圖7 水力直徑對無滑移和有滑移條件下具有不同截面形狀微通道傳熱系數的影響Fig.7 Influence of hydraulic diameter on the heat transfer coefficient of microchannels with different cross-sectional shapes

3 結 論

對具有矩形、橢圓和三角形這3種不同微通道截面形狀的微通道熱沉的傳熱傳質性能進行了研究，得出結論：

a. 當固液界面存在邊界滑移時，微通道熱沉內的流體阻力隨著滑移長度的增加而減小，傳熱系數隨著滑移長度的增加而增大。所以，邊界滑移有助于降低流阻，增強散熱性能。

b. 在相同截面面積條件下，通過調整矩形截面的高寬比、橢圓截面的長短軸之比和等腰三角形截面的頂角及腰長的方式來改變截面尺寸，發現流體阻力隨著水力直徑的增加而減小，傳熱系數隨著水力直徑的增加而減小。相同截面形狀條件下，正方形、圓形和等邊三角形微通道熱沉具有最小的流體阻力和最差的散熱性能。

c. 在相同截面面積條件下，對于具有矩形、橢圓和等腰三角形這3種不同截面形狀的微通道熱沉，三角形微通道熱沉的散熱性能在這三者中最弱；對于矩形和橢圓形微通道熱沉，存在某一臨界值使得水力直徑小于這一臨界值時，矩形微通道熱沉的散熱性能優于橢圓形微通道熱沉，當水力直徑大于這一臨界值時，橢圓形微通道熱沉的散熱能力大于矩形微通道熱沉。

研究表明，引入邊界滑移并合理調整微通道截面形狀和尺寸可以優化微通道熱沉的傳熱傳質性能，這為微通道熱沉的優化設計提供了一定的借鑒。此外，本文研究可以進一步采用實驗進行驗證，利用微量泵驅動流體在微通道熱沉內流動，并通過加熱裝置模擬發熱元件，將熱沉置于其上以模擬整個散熱過程。利用溫度傳感器、壓力傳感器等對實驗過程中的關鍵數據進行測量，并進一步分析得到系統的流阻和熱阻。實驗中應嚴格控制變量，保證微通道橫截面積保持不變，改變截面形狀、尺寸和滑移條件，對于滑移長度的調整可以通過改變管道內表面的粗糙度、溶液的pH等方式實現。