基于貝葉斯網絡算法的發電系統可靠性評估

吳 琳，楊 萌，吳 烜，朱 琳，汪 濤

（1.國家電網湖北省電力有限公司技術培訓中心，湖北 武漢 430014；2.國網武漢供電公司，湖北 武漢 430050）

0 引 言

電力系統的任務是向用戶提供穩定的電能。如果不能保證電能質量，將會造成各種財產損失甚至危及人身安全。現在風力發電和水利發電也在逐步并入電網，可靠性問題分析難度逐漸加深，如何提高核電站及其相關聯的電力系統的可靠性成為當前的主要問題。目前，研究電力系統可靠性的方法有兩種[1]：解析法和模擬法。

解析法包括電力不足概率法（LOLP）、電量不足概率法（LOEP）、頻率及持續時間法（F&D）和電力不足期望值法（LOLE）。以上4種方法，共同特點是組件及系統的壽命過程均用數學模型表示，可靠性指標可以通過求解數學模型得到，特點是物理概念清晰，邏輯關系明確，模型精度高。但是，當系統復雜時，用解析法構造模型十分困難，計算量也會隨系統的規模呈指數關系增長。所以，解析法在系統龐大時會受到限制[2-6]。

模擬法又叫Monte Carlo法，是通過在計算機上用隨機數表示系統中每個元件的概率參數來模擬元件或系統壽命過程的一次實際實現，并按照對此模擬過程進行若干時間的觀察，估計所求的可靠性指標。因為該方法原理簡單、受限因素較少，所以通常用于對大型系統進行可靠性評估。模擬法雖然也要建立數學模型，但其結果是通過在模型上進行采樣試驗求得的，類似于通常的統計實驗，因此其計算量較解析法要小得多。

近年來，人工智能技術逐漸滲透到電力系統可靠性評估領域，用以改進常規方法的不足。例如，屬于模擬法的貝葉斯網絡方法，是以概率推理為基礎的圖形化網絡，最顯著的特點是具有強大的不確定性問題處理能力。因此，基于貝葉斯網絡的方法不僅能方便描述系統最大容量和負荷需求之間的平衡關系，而且能夠有效計算系統失去負荷的概率和其他各種概率。

本文嚴格按照發電系統可靠性分析的基本步驟，在所建立的容量模型的基礎上，運用概率統計方法，對發電系統的可靠性和連續供電能力進行定量分析并評估，在貝葉斯網絡數學模型基礎上建立發電系統的可靠性數據指標，最后用VB仿真程序驗證所得結果。驗證結果顯示，本文所采用的模型和計算方法具有計算精度高、方便易行的優點，克服了目前傳統算法隨著發電機數量的增多過于復雜的缺點，具有普遍的推廣意義。

1 可靠性檢驗的基本模型和方法

系統的備用容量（即系統的裕度）是衡量發電系統可靠性的指標。本文研究的主要指標包括容量的確切狀態概率、頻率和累積狀態概率、頻率。這些指標可以通過由發電系統模型和發電系統可靠性負荷模型結合形成風險模型給予計算[7-10]。

1.1 容量狀態概率模型的基本概念

容量概率模型是指發電機組或系統在某一時刻在某一種容量狀態運行的概率。這種離散型概率分布在實際應用中有兩種表達形式，即可用容量概率模型和停運容量概率模型。因此，可以用這兩種容量概率模型分別表達一臺容量為c（單位：MW）的發電機組。

可用容量概率模型：

停運容量概率模型：

本文采用可用容量概率模型，首先建立3臺機組的容量概率模型，然后逐步增加機組數量，最后形成整個系統的容量概率模型。

1.2 基本方法

本文的分析方法及步驟如下。

步驟1：基于貝葉斯網絡數學算法建立容量模型，對發電系統進行可靠性分析計算。

步驟2：對所建立的孤立系統發電進行可靠性分析，詳細步驟如下：

（1）對機組的可用容量概率進行建模；

（2）對負荷分布的概率進行建模；

（3）將機組可用容量的概率模型與負荷分布概率模型合并，生成電力系統容量適應性的概率模型，通過該適應性概率模型可求得系統的可靠性指標。

根據所建立的3臺機貝葉斯數學模型，推斷出多臺機確切狀態概率及頻率和累計狀態概率及頻率，并根據結果進行可靠性分析的定量計算。

步驟3：在微機上完成實例的演示，并利用仿真驗證模型的有效性和可靠性。

2 發電容量模型

2.1 3臺機容量模型

為了對發電系統做可靠性的定量分析，建立發電容量模型。需要根據以下3條結論[1]進行份詳細分析。

（1）狀態轉移頻率fij=piλ或fij=piμ，其中pi為該狀態的狀態概率，λ為轉出頻率，μ為轉入頻率。

（2）從任意一個狀態轉出到另一個狀態的頻率λ和從另一個狀態轉入到該狀態的頻率μ是相等的，即頻率平衡。

在如上3條結論的基礎上，建立貝葉斯概率模型，對3臺發電機容量模型進行分析。

建立三臺機容量模型如圖1所示，各機組參數如下：機組容量ci(i=1,2,3)，單位MW；故障率λi(i=1,2,3)為1/a；修復率μi(i=1,2,3)為1/a。

2.1.1 狀態模型圖

對于一個有3臺機組的發電系統，各機組相互獨立，應有23=8種組合狀態。圖2給出了一個由3臺機組組成的發電系統的狀態空間圖。

圖1 3臺機容量模型

圖2 3臺機狀態空間圖

2.1.2 狀態概率

3臺發電機組的可用度和不可用度分別為：

因而，連續不可用度為：

累積狀態概率為直接累積相加，即：

2.1.3 狀態頻率

確切狀態頻率，由圖2狀態空間圖，應用fi=的關系可直接寫出：

其中，fi為確切狀態頻率，有

累積狀態頻率，同樣可由狀態空間圖寫出：

上述發電系統容量概率模型的計算步驟和方法，對由任意數量機組組成的發電系統具有普適性。因此，可將其一般公式進行總結。

確切狀態概率為：

累積狀態概率為：

確切狀態頻率為：累積狀態頻率為：

其中，λk+、λk-分別表示k狀態向增大、減小可用容量狀態的轉移率。

2.2 4臺機組及其以上容量模型的遞推公式

雖然應用前文推導的公式可以計算發電系統各容量狀態的概率和頻率，但是缺點明顯。因為當系統中發電機組的數量超過一定數量時，計算將變得困難[10]，問題在于對于計算機性能的要求過高。例如，如果一個發電系統有100臺機組，那么就有2100=1.267 65×1030個狀態量，普通計算機根本無法提供如此巨大的存儲量。為了解決這種問題，本文采用了一種較為快捷的計算方法，如圖3所示。這種方法計算速度快，要求存儲容量小，在一般計算機上即可使用，實用性高。

圖3 容量組合圖解

設ci和cj分別為2個相互獨立發電機組的容量狀態。這2臺機組的狀態概率和狀態頻率分別為：

這2種容量轉臺下的2臺機組同時運行時，形成一種新的狀態J，其容量、概率和頻率分別為：

設發電系統的停運容量狀態已經形成到X（單位：MW），這時狀態X有p(X)、F(X)及λi。當增加1臺容量為c（單位：MW）的發電機組時，雙態停運容量的概率和頻率分別是p、f0、q及fc。從已形成的容量停運概率及頻率表中，取狀態X-c及其相對應的p(X-c)、F(X-c)及λk。這樣有4種相互獨立的停運容量，狀態X和狀態0相組合成為新狀態A，有容量：

同樣，新狀態B有容量：

狀態A和狀態B組合成新的停運容量狀態，可遞推出確切停運容量狀態概率為：

式中pn-1(X)即p(X)，pn-1(X-c)即p(X-c)，表示增加機組以前已形成的停運容量狀態概率；pn(X)表示機組增加后的停運容量狀態概率。

應用此遞推公式（34）計算發電系統停運容量狀態概率時，對第一臺機組令p(0)=p、p(c)=q及X＜c時p(X-c)=0。

計算累積概率，這式中所有概率p(X)均為累積概率值，對第一臺機組p(0)=1.0以及X＜c時p(X-c)=1。

累積狀態頻率為：

這里 pn-1(X)及Fn-1(X)等都是累積狀態值，需要進一步確定新增加機組的狀態頻率f0及fc。由于新機組的0狀態和c狀態是互斥的，因此它們的累積狀態頻率為：

即：

于是，增加一臺機組后累積狀態頻率的遞推公式為：

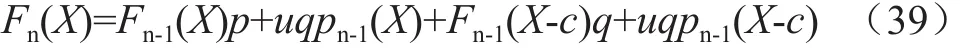
應用此遞推公式的初始條件：當X＜c時，pn-1(X-c)=1以及Fn-1(X-c)=0。使用傳統方法計算系統容量概率時，當系統中發電機組的數量很大時，計算程序上要內存容量很大。例如，如果一個發電系統有100臺機組，那么就有2100=1.267 65×1030個狀態量，對于普通計算機來說，根本無法提供如此巨大的存儲量。而本文方法不僅計算速度快、要求存儲容量小，而而可以不受機組臺數的限制。

3 發電系統的可靠性仿真分析

為了驗證該模型的可行性、有效性和精確性，通過VB程序建立仿真模型，以5臺發電機模型為例，并采用相同原始數據進行校驗理論計算結果，然后通過程序輸出結果對比計算結果。仿真模型流程如圖4和圖5所示。

圖4 5臺發電機流程圖

建立模型所用輸入數據如表1所示，用以對比結果，計算誤差，同時做分析。

仿真結果與計算結果無誤，實際仿真結果與原始數據計算結果值在萬分之一量級上保持一致，說明所建立的模型精確度高，具有高度實用意義。

圖5 5臺發電機降額運行和計劃檢修狀況下的流程

4 結 論

本文建立了3臺機發電系統可靠性的數學模型，以此模型為根據推斷出多臺機發電系統可靠性的數學模型，得到確切狀態概率及頻率和累計狀態概率及頻率。通過高效的貝葉斯網絡推理算法，有效計算系統失去負荷的概率和其他各種概率。仿真結果證明，該模型操作簡單，計算結果準確，精度較高，改善了傳統模型對計算量要求高的缺點。還可以考慮根據其他概率模型，對發電系統可靠性做更多分析，并建議用可靠檢驗的知識來做結果評析。

表1 輸入數據

表2 理論計算結果

表3 部分仿真輸出結果

狀態i 狀態概率p 累積概率p*狀態頻率f 累積頻率f*17/00111 0.000 796 26 0.001 232 13 0.016 403 01 0.026 863 26 16/11000 0.000 060 22 0.000 435 87 0.001 770 40 0.012 371 28 15/10100 0.000 044 70 0.000 375 65 0.001 323 05 0.010 673 15 14/01100 0.000 044 70 0.000 330 95 0.001 323 05 0.009 412 67 13/10010 0.000 044 70 0.000 286 25 0.001 323 05 0.008 152 20 12/01010 0.000 044 70 0.000 241 56 0.001 323 05 0.006 891 73 11/00110 0.000 033 18 0.000 196 86 0.000 988 69 0.005 631 26 10/10001 0.000 044 70 0.000 163 68 0.001 323 05 0.004 695 65 9/01001 0.000 044 70 0.000 118 98 0.001 323 05 0.003 435 18 8/00101 0.000 033 18 0.000 074 28 0.000 988 69 0.002 174 70 7/00011 0.000 033 18 0.000 041 11 0.000 988 69 0.001 239 10 6/10000 0.000 001 86 0.000 007 93 0.000 072 26 0.000 303 49 5/01000 0.000 001 86 0.000 006 07 0.000 072 26 0.000 232 34 4/00100 0.000 001 38 0.000 004 20 0.000 053 91 0.000 161 20 3/00010 0.000 001 38 0.000 002 82 0.000 053 91 0.000 108 39 2/00001 0.000 001 38 0.000 001 44 0.000 053 91 0.000 055 58 1/00000 0.000 000 06 0.000 000 06 0.000 002 78 0.000 002 78