小學(xué)數(shù)學(xué)課融合數(shù)形結(jié)合思想開展教學(xué)之嘗試

安徽省合肥經(jīng)開實(shí)驗(yàn)學(xué)校 冷利娟

數(shù)形結(jié)合思想方法在數(shù)學(xué)教學(xué)方面占據(jù)重要地位，主要是通過數(shù)形之間的相互轉(zhuǎn)化與利用來對數(shù)學(xué)問題進(jìn)行解決，是抽象數(shù)學(xué)語言和直觀圖形有效結(jié)合的體現(xiàn)，也是抽象思維和形象思維相結(jié)合的體現(xiàn)。

一、滲透數(shù)形結(jié)合思想，增強(qiáng)數(shù)學(xué)概念的理解

數(shù)學(xué)概念實(shí)際上是人的大腦對現(xiàn)實(shí)生活中某一對象的數(shù)量關(guān)系及空間形式相關(guān)本質(zhì)特征的一種反映，也可以被稱為數(shù)學(xué)思維形式，其抽象性與邏輯性都比較強(qiáng)。而在數(shù)學(xué)概念的教學(xué)中滲透數(shù)形結(jié)合思想，可以讓學(xué)生對圖形中蘊(yùn)含的數(shù)形關(guān)系進(jìn)行分析，然后直觀地理解相應(yīng)的數(shù)學(xué)概念。比如在蘇教版小學(xué)數(shù)學(xué)三年級“認(rèn)識分?jǐn)?shù)”這部分的教學(xué)中，教師先引導(dǎo)學(xué)生初步認(rèn)識某個整數(shù)的幾分之一，即把某個事物看作一個整體，將其平均分成幾個部分，每個部分都相當(dāng)于這一整體的幾分之一。為了讓學(xué)生有效認(rèn)識分?jǐn)?shù)，教師可滲透數(shù)形結(jié)合思想方法。比如教師將12 根小木棒看作一個整體，將其分成12 份之后，每根小木棒都相當(dāng)于這個整體的。這時教師可以向?qū)W生提出問題：“若是這些小木棒可以代表的分?jǐn)?shù)有等等，那你是否可以將其位置生動地表達(dá)出來？”在這樣的數(shù)學(xué)問題中，數(shù)軸類的圖形可以有效表達(dá)相應(yīng)的位置關(guān)系，將抽象的分?jǐn)?shù)知識轉(zhuǎn)化成為簡單易懂的數(shù)學(xué)內(nèi)容，如圖1 所示：

圖1

圖1 所表示的分?jǐn)?shù)位置有效地體現(xiàn)了分?jǐn)?shù)之間的大小關(guān)系，還能讓學(xué)生直觀地理解每個分?jǐn)?shù)所代表的含義，使學(xué)生深刻認(rèn)識分?jǐn)?shù)這一概念。這是數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)概念教學(xué)過程中得以有效滲透的體現(xiàn)，克服了數(shù)學(xué)概念課程教學(xué)低效化的問題，提高了學(xué)生對數(shù)學(xué)概念的學(xué)習(xí)效果。

二、滲透數(shù)形結(jié)合思想，準(zhǔn)確把握數(shù)學(xué)本質(zhì)

數(shù)學(xué)的抽象性及邏輯性是固有的學(xué)科特點(diǎn)，但是教師卻可采用有效的教學(xué)策略來將抽象的數(shù)學(xué)知識轉(zhuǎn)變成為直觀可感的數(shù)學(xué)內(nèi)容。其中，數(shù)形結(jié)合思想的滲透就可以實(shí)現(xiàn)這一教學(xué)目的，將其應(yīng)用在學(xué)生的數(shù)學(xué)學(xué)習(xí)中，能有效激活學(xué)生的數(shù)學(xué)思維，并將數(shù)學(xué)的本質(zhì)更清晰地呈現(xiàn)在學(xué)生面前，使其準(zhǔn)確把握數(shù)學(xué)知識中蘊(yùn)含的數(shù)學(xué)本質(zhì)。華羅庚很明確地指出：在數(shù)缺形的情況下，直觀性不強(qiáng)；在形缺數(shù)的情況下，則很難觀察入微，難以體現(xiàn)其數(shù)學(xué)本質(zhì)。因此，數(shù)學(xué)教師要提高數(shù)學(xué)課堂教學(xué)效果，就需要滲透數(shù)形結(jié)合思想，讓抽象又復(fù)雜枯燥的數(shù)學(xué)知識可以轉(zhuǎn)化成為直觀又簡單生動的數(shù)學(xué)內(nèi)容，促使學(xué)生的抽象思維與形象思維獲得協(xié)調(diào)性的良好發(fā)展。

比如在蘇教版小學(xué)數(shù)學(xué)四年級“運(yùn)算律”的教學(xué)中，教師就可依托教材來改進(jìn)練習(xí)題目，如：“在同一塊菜地中，將其分成兩個區(qū)域，分別栽種白菜和菠菜。其中栽種白菜的區(qū)域?yàn)殚L與寬分別是25m、6m 的長方形，而栽種菠菜的區(qū)域則是長與寬分別為15m 和6m 的長方形，那么請問它們的面積總共是多少？”有的學(xué)生在解答時將它們合并成為一個大的長方形來進(jìn)行計(jì)算，也有的學(xué)生是分別計(jì)算兩個長方形面積之后，將兩者的面積結(jié)果相加。為了理清其中的數(shù)形關(guān)系，教師可引導(dǎo)學(xué)生繪制出相應(yīng)的圖形。

三、滲透數(shù)形結(jié)合思想，培養(yǎng)學(xué)生的邏輯推理能力

培養(yǎng)學(xué)生的邏輯推理能力是數(shù)學(xué)課程標(biāo)準(zhǔn)對教師提出的重要教學(xué)要求，可以幫助學(xué)生更好地掌握數(shù)學(xué)知識之間存在的內(nèi)在聯(lián)系，以有效理解抽象的內(nèi)在邏輯關(guān)系。尤其是在公式推導(dǎo)方面，教師可以有效鍛煉學(xué)生的邏輯推理能力。而數(shù)形結(jié)合思想方法的滲透可以輔助教師達(dá)到培養(yǎng)學(xué)生邏輯推理能力的教學(xué)目標(biāo)，教師可積極將其滲透在公式推導(dǎo)類的教學(xué)過程中。比如在蘇教版小學(xué)數(shù)學(xué)五年級《三角形面積的計(jì)算》這一課的教學(xué)中，教師要讓學(xué)生合理推導(dǎo)出三角形面積公式，并加強(qiáng)其對這一面積計(jì)算公式的理解，可采取數(shù)形結(jié)合的方法來進(jìn)行教學(xué)。教師在教學(xué)過程中，可為學(xué)生呈現(xiàn)圖2 的幾個三角形幾何圖，讓學(xué)生觀察其中的數(shù)形關(guān)系，并推導(dǎo)三角形面積的計(jì)算公式。

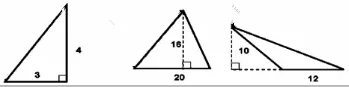
圖2

在公式推導(dǎo)的過程中，為了更好地體現(xiàn)出圖2 中數(shù)形之間的本質(zhì)，可繪圖，如圖3 所示：

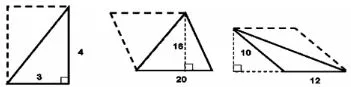
圖3

在求解第一個三角形的面積時，據(jù)圖可知底和高分別是3 和4，可將其面積計(jì)算公式列為：3×4÷2=6。由于原有直角三角形的斜邊與虛線構(gòu)成的三角形和該直角三角形完全相同，共同構(gòu)成了一個長方形，則3×4 代表的是這一長方形的面積。而在求解原有直角三角形面積時需要除以2，主要是因?yàn)檫@一三角形的面積就是該長方形面積的，這也就推導(dǎo)出了直角三角形的面積計(jì)算公式。其中，S 代表的是三角形的面積，而a 和b 分別代表三角形的底和高。通過同樣的公式推導(dǎo)方式，可以繼而推導(dǎo)出圖3 中另外兩個三角形的面積公式。在這一公式推導(dǎo)過程中，學(xué)生可以更容易地理解三角形面積計(jì)算公式和圖形之間的關(guān)系，同時學(xué)生也更清晰地了解到三角形面積和拼成的四邊形面積之間的內(nèi)在聯(lián)系，深刻理解了公式中“”的含義，利于學(xué)生有效記憶和鞏固三角形面積計(jì)算的數(shù)學(xué)知識。

綜上所述，數(shù)形結(jié)合思想應(yīng)用在小學(xué)數(shù)學(xué)教學(xué)中具有重要的教學(xué)價值，小學(xué)數(shù)學(xué)教師應(yīng)該注重滲透這一思想方法，展開有效的課堂教學(xué)活動，促使學(xué)生在數(shù)形結(jié)合思想的指引下有效理解抽象的數(shù)學(xué)知識內(nèi)容，直觀地獲取一些數(shù)量關(guān)系，可提高學(xué)生在數(shù)學(xué)學(xué)習(xí)中的解題效率。