炸藥爆轟熱力學數據非線性擬合方法研究?

杜明燃 張金龍 梁琳娜 黃亮亮 韓體飛 劉 鋒

安徽理工大學化學工程學院(安徽淮南，232001)

引言

研究炸藥性能時，爆轟參數一直都是備受關注的課題，它是預測炸藥性能和理論設計炸藥的基礎[1]。為計算炸藥爆轟參數，國內外學者提出了BKW、JWL、LJD、JCZ3和 WCA 等物理模型[2-7]，并發展了相關計算程序，對理論研究爆轟參數作出了重大貢獻。研究發現，利用BKW[3]、WCA和LJD等狀態方程計算爆轟參數時，爆轟參數的求解過程是一個反復迭代的過程，求解爆溫的熱力學參數若滿足一種函數關系，對設計程序自循環求解爆轟參數具有重要意義。

以往研究者在研究爆溫時多采用Kast平均熱容法[8-9]，這種計算方法基于平均熱容建立，在精確計算中存在不足，導致爆轟參數計算得不準確。從理論角度分析，能量守恒法[9]計算爆溫具有較高的精度，然而，由于理論數據的缺失，能量守恒最終確定的爆轟溫度一般根據理論數據估算得出；同時，在編程計算中發現，爆轟產物一般十余種，若不對熱力學參數進行處理，能量守恒法需要反復迭代大量數據，程序繁瑣[10]且容易出錯。因此，利用擬合的方法確定一種函數關系變得非常必要，在此基礎上再建立求解爆轟參數的數學模型，對求解爆轟參數及爆炸物品的應用具有一定參考意義。

本文中，采用非線性擬合的方法處理爆轟產物熱力學數據，比較非線性擬合法與Kast平均熱容法計算物質的焓變(HT-H298)與理論值的差別。在保證非線性擬合方程精度的基礎上，依據此非線性擬合方程建立求解爆轟參數的數學模型，模型選取BKW狀態方程作為爆轟產物的狀態方程，利用最小自由能原理和Hugoniot關系，最終編程實現此過程。利用此程序，求解RDX和硝基甲烷(CH3NO2)的爆溫、爆壓、爆速和爆轟產物組成，驗證此方法的可行性。

1 炸藥爆轟溫度的確定方法

1.1 Kast平均熱容法

計算炸藥爆轟溫度常用的方法是爆轟產物平均熱容法[8]。爆轟產物平均熱容法是利用在一定溫度范圍內物質的平均熱容計算爆轟溫度，物質的平均熱容由經驗公式確定。爆轟產物平均熱容法的計算公式如下：

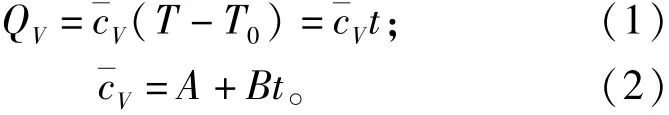
式中：QV為炸藥定容爆熱，kJ/mol；為爆轟產物的平均熱容；T為爆溫，K；T0=298.15 K；t為溫差；A、B為平均熱容的線性系數。

1.2 能量守恒法

能量守恒法[9]利用物質能量守恒確定爆溫，能量守恒法滿足如下計算公式：

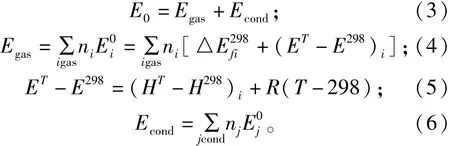
1.3 非線性擬合法

能量守恒法具有嚴格的理論依據，但能量守恒法與Kast平均熱容法相比也具有一個重要缺陷：理論數據不足，導致部分計算只能停留在估算階段，給爆溫的確定帶來誤差，導致計算其他爆轟參數也出現誤差。因此，依據能量守恒法建立模擬物質的熱力學關系的方程變得十分必要。依據式(4)、式(5)和式(6)，可以得出以下假設公式：

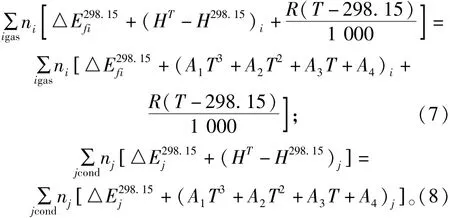
式中：A1、A2、A3、A4為待擬合系數，可以根據最小二乘法編程計算得到，編程依據熱化學參數可由文獻[11]獲得。

式(7)、式(8)確定后，可以依據式(3)建立確定爆溫的能量守恒公式。表1給出了爆轟產物對應系數的擬合結果，爆轟產物中的碳單質視為金剛石[12-18]。表1適應范圍為298～5 000 K。為比較線性擬合法與平均熱容法計算方法的準確度，分別利用Kast平均熱容法和非線性擬合法計算CO2、H2O和N2的焓變(HT-H298)，共7組數據。表2列出兩種方法計算所得的3種主要產物的焓變(HT-H298)與理論值[11]。

表2顯示，對于CO2、H2O和N2，Kast平均熱容法的計算誤差遠遠大于本工作所采用的非線性擬合法。表2中，非線性擬合法的最大誤差為0.5%；Kast平均熱容法的計算最小誤差為3.1%，最大誤差為12.5%。

2 求解爆轟參數過程

2.1 BKW狀態方程

BKW狀態方程[10]最初是由Becker提出的，后來經過Kistiakowsky和Wilson等的修正，最后確定為以下形式：

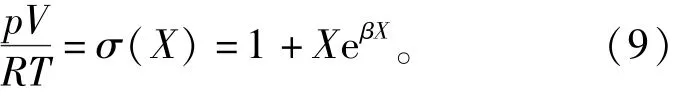
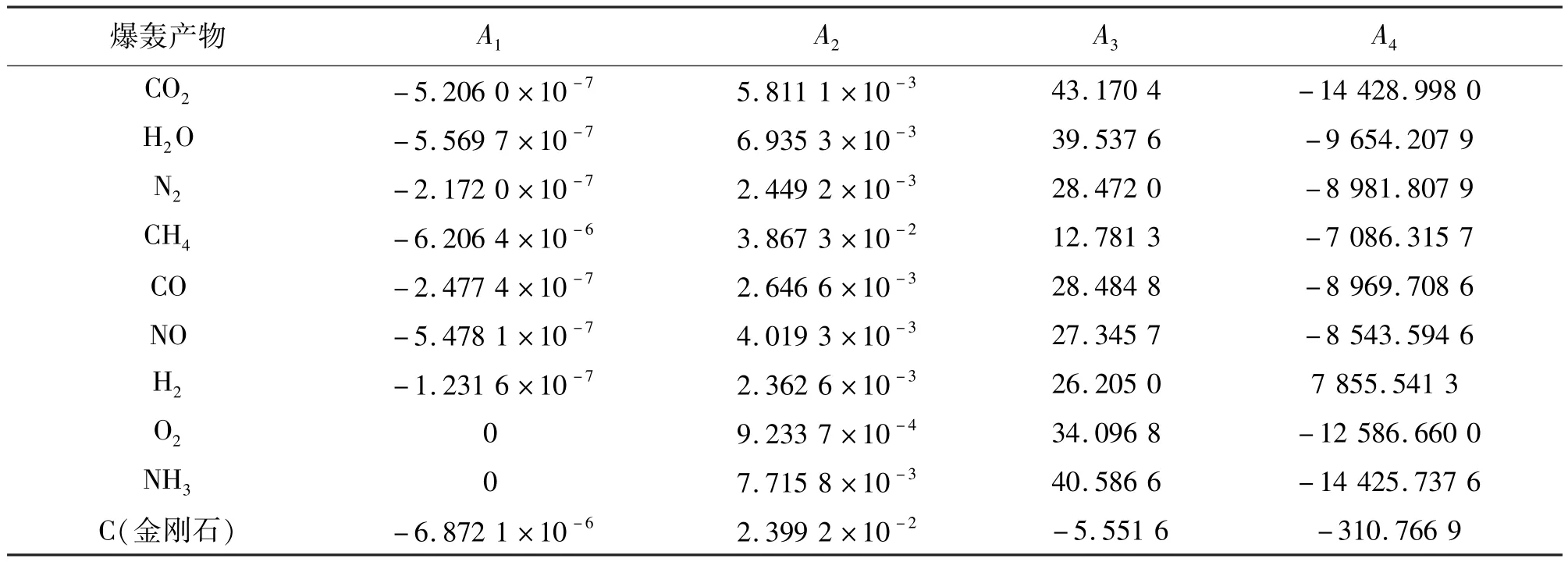
表1 式(7)和式(8)系數的擬合值Tab.1 Fitting values of coefficient for Eq-7 and Eq-8

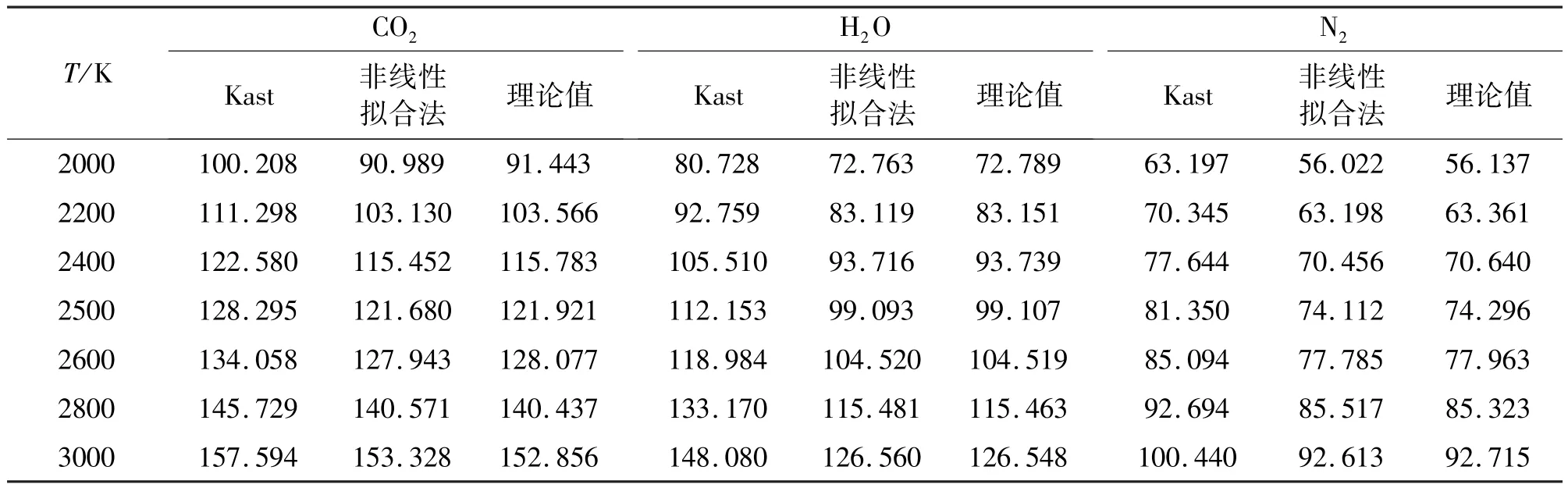
表2 焓變(HT-H298)的計算與理論比較Tab.2 Calculation results and theoretical values of(HT-H298) kJ/mol

式中：p為爆轟壓力，Pa；β為常數；X=κ∑xiki/V(T＋θ)α；V為爆轟氣體摩爾體積，κ、α、θ為經驗常數，ki為第i種物質的余容，xi為這種物質的摩爾分數。

2.2 求解爆轟參數的數學模型及模擬算法

利用最小自由能原理建立非線性方程組。根據質量守恒和物質自由能公式，再運用拉格朗日乘數法把條件極值轉化為非條件極值，可以得出與爆轟產物系統具有相同極值條件的公式：

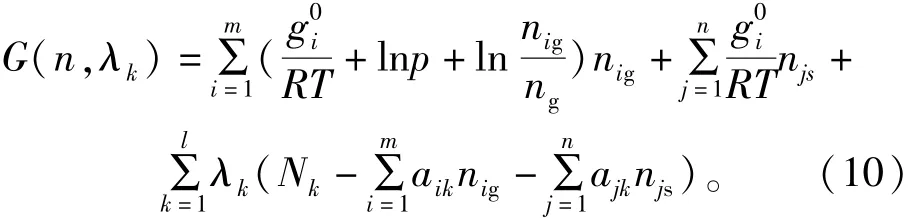
式中：G、g、g0分別為爆轟體系自由能、物質自由能和標準狀況下自由能，kJ/mol；Nk為1 kg爆炸產物含有第k種元素的物質的量；λ為拉格朗日因子；k為第k種元素序號；λk為第k種元素的拉格朗日因子；i為第i種氣體產物序號；j為第j種固體產物序號；aik為每摩爾第i種氣相組分含有k元素的物質的量，mol；ajk為每摩爾第j種凝聚相組分含有k元素的物質的量，mol；ng為氣體產物總物質的量；nig為第i種氣體的物質的量；njs為第j種固體的物質的量；l為炸藥所含元素的種類數；m和n分別為氣體和固體的種類。

式(10)對應極值條件的方程組為非線性方程組，為求解此方程組，根據本小組研究的牛頓迭代法求解非線性方程組的思路[19]，利用以下模型求解爆轟參數和爆轟產物組成。

首先，需要把 ?G(n，λk)/?nig、?G(n，λk)/?njs和?G(n，λk)/?λk看作是關于nig、njs和λk的方程組，令

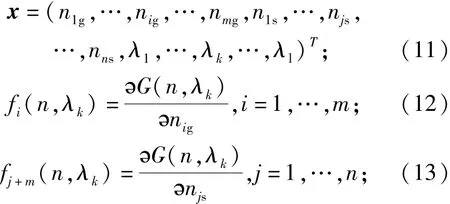
把式(11)、式(12)、式(13)和式(14)代入式(16)，可求得F′(x)，進一步求得F′(x)-1，并記解為x(k＋1)，對應牛頓迭代法公式：x(k＋1)=xk-F′(xk)-1F(xk)，求解上述公式要先假設一組爆溫T′和爆壓p′，此溫度和壓力可以根據一般經驗計算值確定，再取經驗計算所得爆炸產物組分量并作一定變換后，作為初始近似根x1，設置計算精度ε=0.000 001，即xk和x(k＋1)對應元素的誤差絕對值。

炸藥爆轟氣相產物分子體系必須滿足Hugoniot關系[10，20]：

爆速表達式為

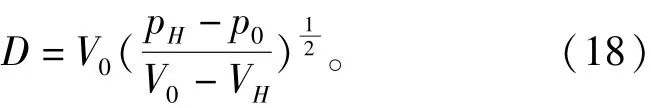
根據BKW狀態方程、以上求解模型和本文中設計的爆轟產物非線性擬合方程，計算爆溫T和爆壓p，與假設爆溫T′和爆壓p′比較，反復修正，直到滿足假設值與計算所得值相同。

以上求解爆轟參數的數學模型利用自編程序實現，計算過程詳見本課題組前期研究工作[19]，其程序算法框圖見圖1。

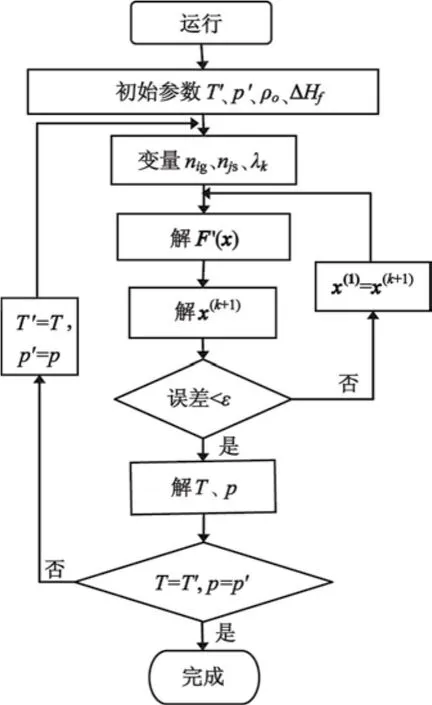
圖1 計算模擬程序圖Fig.1 Computer simulation program chart

3 爆轟參數計算結果與分析

利用非線性擬合方法求得密度為1.80 g/cm3的RDX和密度為1.14 g/cm3的CH3NO2的爆轟產物組成，如表3所示，爆轟參數如表4所示。

計算過程BKW狀態方程參數[10]α取0.5，β取0.16，θ取400，κ取10.91。碳的單質生成物為金剛石[12-18]。RDX和CH3NO2的生成熱分別是-70.66 kJ/mol和 113.09 kJ/mol。

為對比本文中計算方法的精確性，表4還分別給出爆轟參數的實驗結果和依據Kast計算爆溫所得結果。

表4顯示，采用非線性擬合法作為計算爆溫的方法計算爆轟參數，比使用Kast平均熱容法計算的數值更加接近實驗值。

對于RDX，非線性擬合法計算爆溫、爆壓和爆速與實驗值的誤差分別為3.3%、0.4%和0.3%；Kast平均熱容法計算爆溫、爆壓和爆速與實驗值的誤差分別為6.4%、3.4%和2.0%。

表3 每摩爾炸藥CJ點爆轟產物組成Tab.3 Detonation products of explosives at CJ point mol

表4 RDX和CH3NO2的爆溫、爆壓和爆速Tab.4 Detonation temperature，pressure and velocity of RDX and CH3NO2

對于CH3NO2，非線性擬合計算的爆溫值也比Kast平均熱容法更接近實驗值。

4 結論

1)采用最小二乘法法得到爆轟產物熱力學參數的非線性擬合方程，與Kast平均熱容法比較，非線性擬合法在計算物質焓變(HT-H298)時顯示出更好的計算精確性。

2)在此基礎上，利用自編程序實現爆轟產物組成、爆壓、爆溫和爆速的計算。密度為1.80 g/cm3的RDX和密度為1.14 g/cm3的CH3NO2的爆轟參數計算結果顯示，采取非線性擬合法計算的爆轟參數比采用Kast平均熱容法計算的結果更加接近實驗值，顯示出更好的應用前景，對炸藥爆轟性能預測具有一定參考價值。