數(shù)形結(jié)合在小學(xué)數(shù)學(xué)課堂教學(xué)中的運(yùn)用

蔣麗美

（湄洲灣北岸經(jīng)濟(jì)開發(fā)區(qū)東埔中心小學(xué)，福建 莆田 351153）

數(shù)學(xué)教育是一種文化，數(shù)學(xué)教育與人的素養(yǎng)發(fā)展相結(jié)合，是數(shù)學(xué)學(xué)習(xí)的真正目的。數(shù)學(xué)具有高度的抽象性、系統(tǒng)性。如何與核心素養(yǎng)相聯(lián)系，筆者認(rèn)為，數(shù)形結(jié)合思想可以架起橋梁，化抽象為具體，化復(fù)雜為簡約，真正助學(xué)生一臂之力，讓學(xué)生借助數(shù)形結(jié)合自主探究、合作交流、深刻理解，逐漸提升數(shù)學(xué)素養(yǎng)。

一、運(yùn)用數(shù)形結(jié)合進(jìn)行計算教學(xué)，發(fā)展數(shù)學(xué)核心素養(yǎng)

運(yùn)算能力是數(shù)學(xué)的“十大核心詞”之一，是學(xué)生必備的數(shù)學(xué)素養(yǎng)。如何讓學(xué)生擁有強(qiáng)大的計算能力？筆者認(rèn)為要讓學(xué)生掌握抽象的算法，應(yīng)該先讓學(xué)生經(jīng)歷算法的探究過程，在探究過程中明白算理。而要讓抽象的算法易于理解，直觀圖是第一幫手。借助直觀圖數(shù)形結(jié)合，可以讓數(shù)的抽象和圖的直觀對應(yīng)起來，讓學(xué)生真正理解算理，掌握計算方法，為形成一定的運(yùn)算能力打好基礎(chǔ)。例如：三年級學(xué)生學(xué)習(xí)《兩位數(shù)乘兩位數(shù)（不進(jìn)位）》中，豎式計算從“兩位數(shù)乘一位數(shù)”跨越到“兩位數(shù)乘兩位數(shù)”是學(xué)生認(rèn)知上的一次大飛躍，探索算法是本課時的重點(diǎn)，理解算理自然而然是難點(diǎn)。“每套書有14本，王老師買了12套，一共買了多少本?”在探究14×12=（）環(huán)節(jié)，可以引導(dǎo)學(xué)生把每本書看成一個點(diǎn)，給學(xué)生提供14×12的點(diǎn)子圖，讓學(xué)生借助點(diǎn)子圖把怎樣算的想法表示出來。時間在一分一分中流逝，學(xué)生的思維火花在點(diǎn)子圖中綻放。學(xué)生依托點(diǎn)子圖，想法百花齊放。

圖1

小小的點(diǎn)子圖，充分展現(xiàn)了不同學(xué)生的思維軌跡，加上算式搭配，完美組合，學(xué)生不用解釋，道理已在數(shù)形結(jié)合中。“仔細(xì)觀察，這些方法有什么共同的特點(diǎn)？”學(xué)生通過交流發(fā)現(xiàn)，這些方法都體現(xiàn)了“先分后合”的解題思路，是把新知轉(zhuǎn)化成已學(xué)過的舊知解決問題，是學(xué)生所積累的探究經(jīng)驗(yàn)的流露，體現(xiàn)了解決問題方法的多樣化。接著，教師可以讓學(xué)生嘗試用豎式計算。“你知道先算什么，再算什么嗎？”教師把說理的機(jī)會拋給學(xué)生。“仔細(xì)觀察，哪幅圖能恰當(dāng)?shù)伢w現(xiàn)豎式的計算過程？”學(xué)生帶著問題在觀察、交流中發(fā)現(xiàn)豎式與圖1-（4）有著密切的聯(lián)系。他們驚奇地發(fā)現(xiàn)豎式其實(shí)就是先計算2套書有多少本，再計算10套書有多少本，最后合起來是12套書的總本數(shù)。直觀的點(diǎn)子圖有效地緩沖了學(xué)生在理解豎式算理中的難度，使豎式計算有圖可依，有理可循，真正做到化抽象為形象。

圖2

圖3

“豎式計算中用到的4句口訣（二四得八、一二得二、一四得四、一一得一）計算的是哪一部分（圖2）為什么第二層的積要錯位寫？能在點(diǎn)子圖上找到豎式計算的過程并說明道理嗎（圖3）”

這樣，借助點(diǎn)子圖尋覓豎式計算的足跡，真正理解錯位寫的道理，突破教學(xué)難點(diǎn)，讓學(xué)生真正明白豎式計算的道理，知其然而知其所以然。3次數(shù)形結(jié)合充分說明了數(shù)學(xué)知識是抽象的，但可以借助圖形來說明道理，“以形助數(shù)更直觀，數(shù)形結(jié)合明道理”。這樣的課堂，學(xué)生不僅收獲了知識，而且培養(yǎng)了幾何直觀意識，積累了以形助數(shù)的探究經(jīng)驗(yàn)，發(fā)展了推理能力，數(shù)學(xué)核心素養(yǎng)的培養(yǎng)正在悄悄地進(jìn)行。

二、運(yùn)用數(shù)形結(jié)合進(jìn)行概念教學(xué)，發(fā)展數(shù)學(xué)核心素養(yǎng)

數(shù)學(xué)概念是對現(xiàn)實(shí)世界的數(shù)量關(guān)系和空間形式的概括反映，它是用數(shù)學(xué)語言和符號揭示事物本質(zhì)屬性的思維形式，是對數(shù)學(xué)知識點(diǎn)的高度濃縮，它以文字的形式呈現(xiàn)，具有很強(qiáng)的抽象性。而小學(xué)生的思維以具體形象思維為主，對抽象的數(shù)學(xué)概念往往感到茫然，無法理解。因此，教師要善于運(yùn)用數(shù)形結(jié)合，借助“形”來呈現(xiàn)概念中所描述的知識點(diǎn)，化解概念中純文字的抽象，讓學(xué)生在豐富的感性材料中建立清晰的表象，掌握概念的本質(zhì)屬性，從而建構(gòu)清晰的數(shù)學(xué)概念。

例如，三年級學(xué)生在學(xué)習(xí)《認(rèn)識幾分之一》中，學(xué)生以前接觸的事物都可以用整數(shù)表示，分?jǐn)?shù)的認(rèn)識是學(xué)生認(rèn)識中的一次飛躍。當(dāng)一個月餅要平均分給2個人的時候，該用什么數(shù)表示？學(xué)生的認(rèn)知里遇到了障礙。很多學(xué)生會說出“一半”，至于“一半”該用什么數(shù)表示？他們就無從知道了。當(dāng)教師介紹“把一個月餅平均分成2份，每份是這個月餅的二分之一，寫作1/2”時，學(xué)生對1/2并不理解。這時就必須借助圖形的幫忙了。教師可以設(shè)計兩個活動幫助學(xué)生建立表象。

活動一：每組學(xué)生各準(zhǔn)備一個圓形、一個長方形、一個正方形，讓學(xué)生表示出圖形的1/2（見圖4）。當(dāng)學(xué)生展示時，教師引導(dǎo)思考：圖形不同，為什么它們都可以用1/2表示？學(xué)生借助圖形發(fā)現(xiàn)不管什么圖形，只要把它平均分成2份，其中的一份都可以用1/2表示。活動二：讓每個學(xué)生用一張正方形紙表示1/4，由于學(xué)生的折法不同，涂色部分的形狀也就不同。（見圖5）

圖4

教師再次引發(fā)思考：陰影部分的形狀不同，為什么它們都可以表示成1/4？通過兩個活動中圖形的介入，學(xué)生對分?jǐn)?shù)1/2、1/4有了感性的認(rèn)識，他們清楚地認(rèn)識到：只要把一個圖形平均分，其中的一份都可以用分?jǐn)?shù)表示。這樣，有了圖形的支撐，“以形補(bǔ)數(shù)”，有效地填補(bǔ)了學(xué)生學(xué)習(xí)分?jǐn)?shù)時形象思維的空白，促進(jìn)了學(xué)生對分?jǐn)?shù)概念本質(zhì)屬性的理解，以形象促抽象，發(fā)展了觀察、分析、實(shí)踐能力，促進(jìn)了幾分之一模型的建構(gòu)，有效地發(fā)展了數(shù)學(xué)核心素養(yǎng)。

圖5

三、運(yùn)用數(shù)形結(jié)合進(jìn)行規(guī)律探尋，發(fā)展數(shù)學(xué)核心素養(yǎng)

數(shù)學(xué)是一門嚴(yán)謹(jǐn)、思維含量高的學(xué)科，探索規(guī)律在數(shù)學(xué)學(xué)習(xí)中占有很大的比例。由于小學(xué)生的思維以具體形象思維為主，對抽象的規(guī)律，往往無從入手，這時，如果能數(shù)形結(jié)合，定能一路高歌，順利攻破。如：學(xué)生在探索連續(xù)奇數(shù)和的計算方法中，教師給學(xué)生出示“1+3+5+7+9+11+13+15+17+…+99=（ ）”，如果單純憑借數(shù)據(jù)探索，學(xué)生探究起來有一定的難度。機(jī)智的學(xué)生想到“化繁為簡”先探索“1+3+5+7+9=（ ）”，這是學(xué)生探究經(jīng)驗(yàn)發(fā)揮的作用。教師給每組學(xué)生提供了必要的學(xué)具，“怎樣擺出這些圖形，可以很快計算算式的得數(shù)？”學(xué)生帶著問題，借助圖形先獨(dú)立思考，并嘗試擺一擺，方格圖在學(xué)生的手中玩起了魔術(shù)。展示學(xué)生智慧的時間到了。如下圖：

圖6

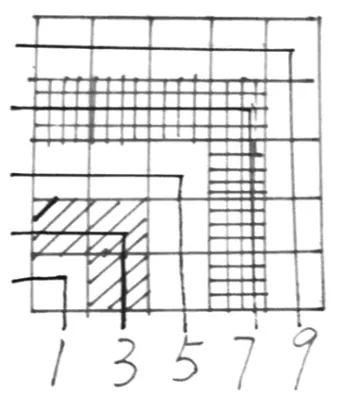
圖7

很顯然，擺成圖7的學(xué)生引起了大家的關(guān)注。

“你這樣擺的目的是什么？”在交流中發(fā)現(xiàn)原來學(xué)

生把它擺成正方形，1+3+5+7+9=（ ）轉(zhuǎn)化成正方形的個數(shù)： 5×5=25。”至于“5”是哪來的？學(xué)生借助直觀圖不難看出，表示的是這組數(shù)的個數(shù)。顯然，學(xué)生們初步學(xué)會用數(shù)學(xué)的眼光觀察圖形，借助圖形用數(shù)學(xué)的思維分析問題，把連續(xù)奇數(shù)的和轉(zhuǎn)化為正方形的總個數(shù)，這樣的探究活動是否有價值？教師繼續(xù)追問。1+3+5+7+9+11=（ ），照這樣擺下去，可以擺成邊長是幾的正方形？1+3+5+7+9+11+13+15+17+…+99=（ ）呢？

就這樣借助圖形數(shù)形結(jié)合，學(xué)生經(jīng)歷操作、想象、交流、分析，初步發(fā)現(xiàn)“連續(xù)的奇數(shù)和，有幾個就是幾的平方”的結(jié)論。這時，教師拋出“3+5+7+9+11+13”，有5個數(shù)，就是5的平方等于25，對嗎？”機(jī)智的學(xué)生再次結(jié)合圖形說理，如果少了1，這些數(shù)就不能拼成正方形了，從而更加嚴(yán)謹(jǐn)?shù)匮a(bǔ)充規(guī)律：“從1開始的連續(xù)奇數(shù)和，等于個數(shù)的平方”。這樣，學(xué)生在學(xué)習(xí)中做到了“見數(shù)思形、以形助數(shù)”，真正認(rèn)識到“數(shù)形結(jié)合百般好”。此過程拓展了學(xué)生的思維，發(fā)展了探究能力，質(zhì)疑、歸納能力，同時模型思想也在落地生根，數(shù)學(xué)核心素養(yǎng)在悄然生長。

實(shí)踐證明，數(shù)形結(jié)合在學(xué)生的數(shù)學(xué)學(xué)習(xí)中發(fā)揮著重要的作用，數(shù)在左，形在右，數(shù)形結(jié)合如影隨形。數(shù)形結(jié)合搭建了學(xué)生從具體形象思維向抽象邏輯思維發(fā)展的橋梁，積累了活動經(jīng)驗(yàn)，提升了學(xué)生的推理能力、探究經(jīng)驗(yàn)，有效促進(jìn)了數(shù)學(xué)核心素養(yǎng)的發(fā)展。