并聯驅動雙向偏轉平臺設計與動力學分析
陳 純 徐永帥 王佳偉 房 舟 魏碧輝
(陜西理工大學機械工程學院, 漢中 723001)
0 引言
與傳統的串聯機構相比,并聯機構具有精度高、響應快、易于控制等優點,引起了國內外專家、學者的極大興趣[1-2]。而結構簡單、作業空間大、動力學求解簡單、運動耦合度小、對機械零部件加工制造精度要求不高,以及對機構運動控制精度要求較低的少自由度并聯機構更受到青睞[3-7],許多學者對不同類型的并聯機構進行了動力學分析[8-19]。目前學者們提出的并聯機構多以Stewart、Tricept為原形的桿結構類型為主,本文提出一種并聯驅動雙向偏轉平臺,運用Lagrange法建立平臺動力學模型并進行仿真分析。
1 并聯驅動雙向偏轉平臺機構
1.1 機構描述
并聯驅動雙向偏轉平臺如圖1所示,平臺主要由底座、滑塊、電機、驅動拱、圓弧導軌、銷軸、動平臺、主動齒輪以及支撐板等構件組成,圓形動平臺由在空間呈正十字交錯且同心的兩個半圓形外齒輪環(半徑大小不同,稱之為驅動拱)支撐,其中大驅動拱通過銷軸8由轉動副與動平臺連接,小驅動拱通過銷軸11由一種特殊的運動副(稱為滑伸副)與動平臺相連;大小驅動拱分別與半徑不同的圓弧導軌(稱為大、小圓弧導軌)相固聯并由圓弧導軌副(分別由大圓弧導軌與滑塊2、14,小圓弧導軌與滑塊6、13組成)導向,滑塊固聯于置于底座1上的呈正十字布置的支撐板上,大、小驅動拱的偏轉分別由主動齒輪16、15驅動,主動齒輪16、15分別安裝在電機17、3的主軸上,電機17、3固定于底座上,從而實現動平臺繞X、Y軸兩個方向上的大角度偏轉。
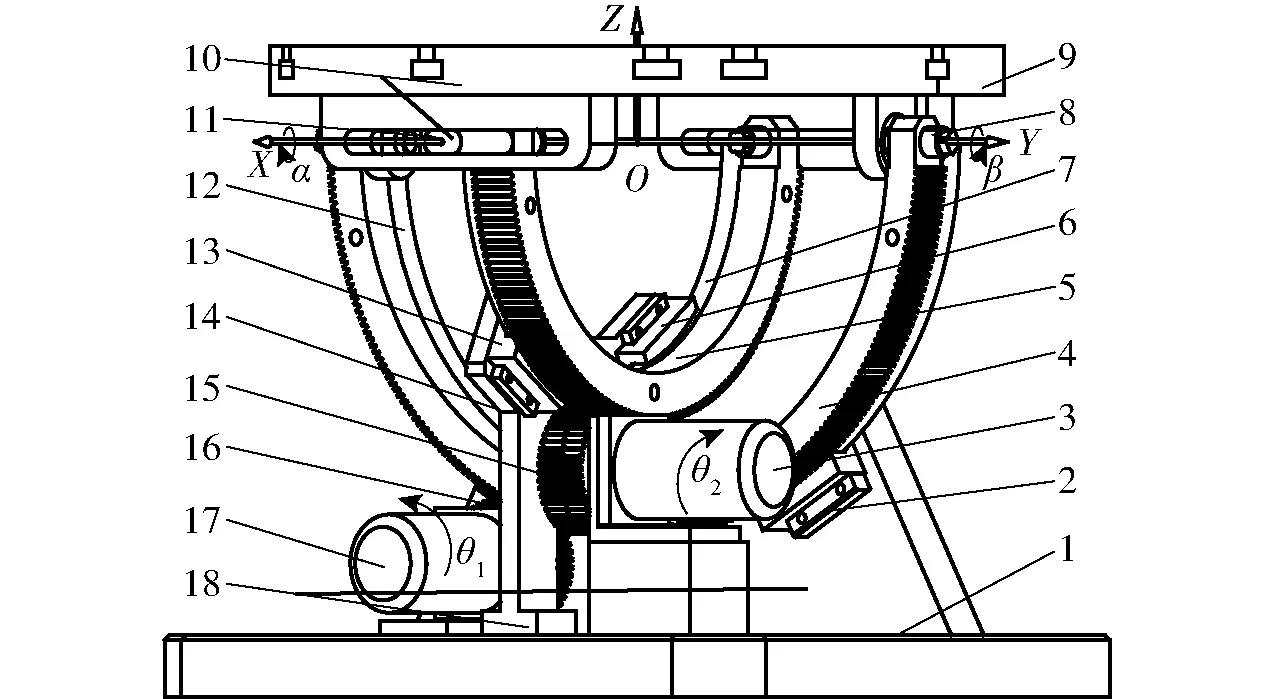
圖1 并聯驅動雙向偏轉平臺模型Fig.1 Parallel bidirectional deflection platform model1.底座 2、6、13、14.滑塊 3、17.電機 4.大驅動拱 5.小驅動拱 7.小圓弧導軌 8、11.銷軸 9.動平臺 10.滑伸副 12.大圓弧導軌 15、16.主動齒輪 18.支撐板
在該平臺中存在一種特殊的運動副(滑伸副10),如圖2所示,該運動副在動平臺同時作繞X軸和Y軸運動的過程中,與小驅動拱連接的銷軸11會在與平臺固聯的U型孔中滑移并伸縮。

圖2 滑伸副Fig.2 Sliding telescopic pair
1.2 自由度分析
在此平臺中,由于大驅動拱的中心與銷軸11的軸線共線、小驅動拱的中心與銷軸8的軸線共線,且平臺分別相對于XOZ、YOZ面對稱,可看作該平臺是沿對稱面切分為含有4條支鏈的并聯機構。由于4條支鏈中對稱面兩邊的兩條支鏈結構完全相同,故該并聯機構可認為是2-GRR(FR)/GRR運動鏈形式的并聯機構,其中G為齒輪副、F為平面副、R為轉動副,滑伸副(FR)可看作是由平面副F和轉動副R組合而成。采用修正的Kutzbach-Grnbler公式[20]計算其自由度
(1)
式中K——機構的自由度
n——包括機架的構件數目
g——運動副的數目
fi——第i個運動副的自由度
v——多環并聯機構在去除公共約束因素后的冗余約束數目
ξ——機構中存在的局部自由度
為了增加并聯機構的剛性和導向精度,此并聯機構中大、小圓弧導軌副中分別含有兩個滑塊,因此該機構中含有兩個冗余約束,即v=2;該機構中不含局部自由度,即ξ=0,其余未知量均較易得出,此處不再詳細分析。
2 運動學逆解
如圖1所示,假定動平臺繞X軸與Y軸偏轉角分別為α和β;主動齒輪15、16轉動角分別為θ1和θ2;主動齒輪15與小驅動拱的齒數分別為z1和z2,模數為m1;主動齒輪16與大驅動拱的齒數分別為z3和z4,模數為m2。
動平臺在繞X軸方向上位置解為
(2)
動平臺繞Y軸偏轉可簡化為圖3所示的幾何關系,假設當動平臺繞X、Y軸偏轉角為α、β,由于滑伸副的存在使得小驅動拱轉角并不等于β,而是β1,其空間關系如圖3所示。

圖3 動平臺繞Y軸偏轉示意圖Fig.3 Schematic of deflection of moving platform around Y axis
由圖3空間幾何關系可得
(3)

(4)
將式(2)、(4)寫成矩陣的形式
(5)
對式(5)求其對時間的一階導數即可得平臺速度逆解,即
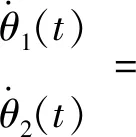
(6)
則并聯驅動雙向偏轉平臺的速度Jacobian矩陣為
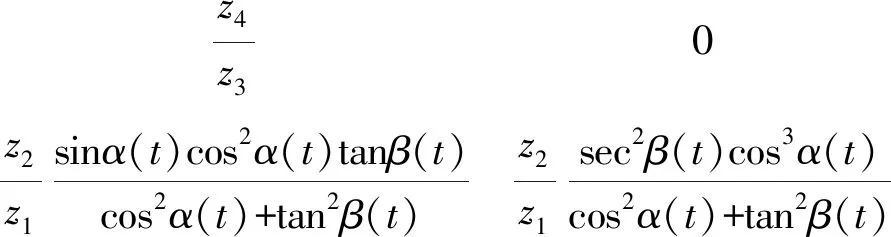
(7)
從平臺的運動學方程可以得出,平臺在繞X軸方向的偏轉運動不受其繞Y軸方向偏轉運動的影響;平臺在繞Y軸方向的偏轉運動受其繞X軸方向偏轉運動的影響,存在耦合關系。
3 平臺動力學建模
平臺總動能T可表示為
T=∑Ti(i=4,5,7,8,9,11,12,15,16)
(8)
式中i——構件編號(圖1)
其中構件4、5、7、12的動能可表示為
(9)

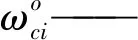
構件8的動能可表示為
(10)
構件11的動能可表示為
(11)
式中I11——構件11在自傳回轉軸下轉動慣量
ωc11——構件11在自傳回轉軸下角速度
構件9的動能可表示為
(12)
構件15、16的動能可表示為
(13)

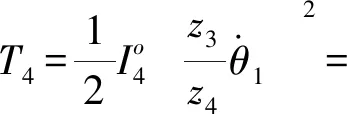
則可得平臺總動能T為
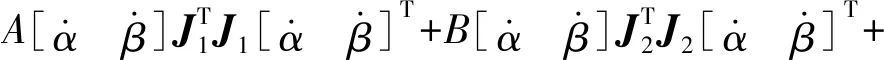
(14)
其中
根據虛功原理可得
QkΔqk=∑δW′=MΔφ+MkΔqk(k=1,2)
(15)
其中
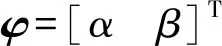
式中M——動平臺所受的外力矩
Δφ——動平臺的偏轉角
Mk——電機輸出的驅動力矩
qk——輸入廣義坐標
Qk——廣義坐標下的廣義力
對式(15)兩邊同時除以Δqk得
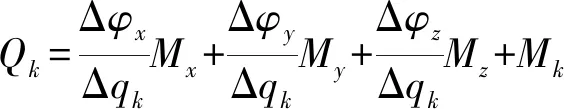
(16)
整理式(16)可得
(17)
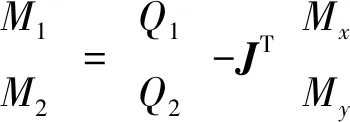
(18)
Lagrange方程為
(19)
將式(14)代入式(18)得
(20)
(21)
(22)
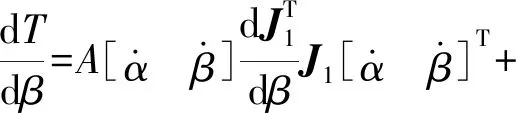
(23)
將式(20)~(23)代入式(19)得
(24)
(25)
將式(24)、(25)代入式(18)得平臺的動力學模型為
(26)
4 動力學計算與仿真
依據所建立的并聯驅動雙向偏轉平臺的動力學模型,給出平臺的參數以及施加在其上的外載,即可計算、仿真電機輸出的驅動力矩。
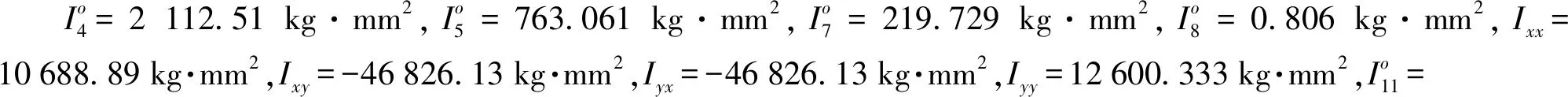
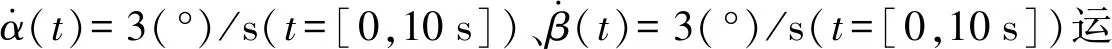
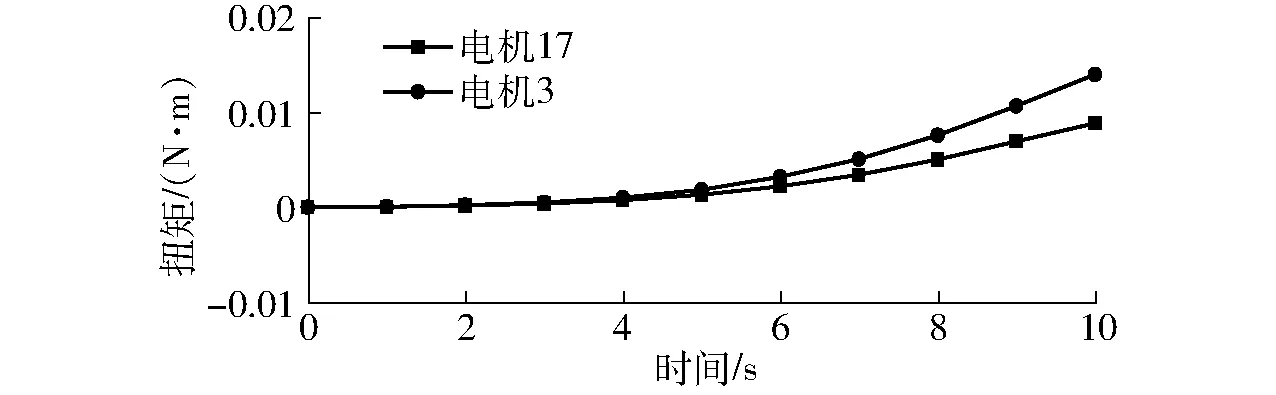
圖4 空載時M1、M2曲線Fig.4 Curves of M1 and M2 under no load
由圖4可知,驅動電機17輸出力矩M1最大為0.009 1 N·m、最小為0.000 6 N·m;驅動電機3輸出力矩M2最大為0.014 2 N·m、最小為0.001 1 N·m。
(2)動平臺9受外力矩Mx=4 N·m、My=0,得出驅動電機3、17輸出的驅動力矩M2、M1變化曲線,如圖5所示。
圖5中驅動電機17輸出力矩M1最大為25.443 2 N·m、最小為25.431 2 N·m;驅動電機3輸出的力矩M2最大為3.426 9 N·m、最小為0.006 7 N·m。
(3)動平臺9受外力矩Mx=0、My=4 N·m,得出驅動電機3、17輸出的驅動力矩M2、M1變化曲線,如圖6所示。
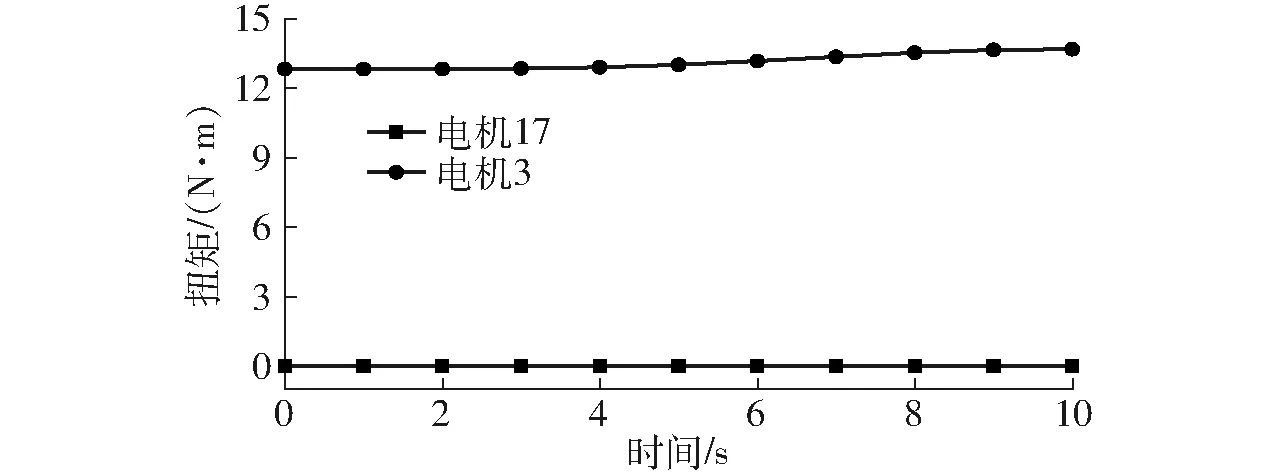
圖6 繞Y軸帶載時M1、M2曲線Fig.6 Curves of M1 and M2 when loading around Y axis
由圖6可知,驅動電機17輸出力矩M1最大為0.009 1 N·m、最小為0.000 6 N·m;驅動電機3輸出力矩M2最大為13.658 2 N·m、最小為12.802 3 N·m。
(4)動平臺9受外力矩Mx=My=4 N·m,得出驅動電機3、17輸出的驅動力矩M2、M1變化曲線,如圖7所示。
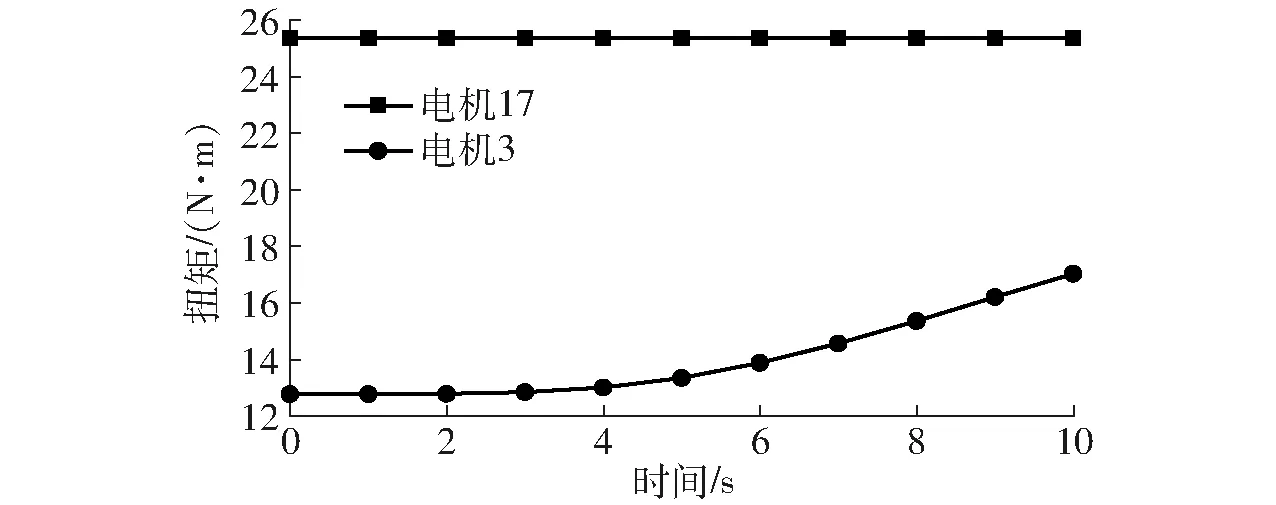
圖7 繞X、Y軸均帶載時M1、M2曲線Fig.7 Curves of M1 and M2 when loading around X and Y axes
圖7中驅動電機17輸出力矩M1最大為25.443 2 N·m、最小為25.441 2 N·m;驅動電機3輸出力矩M2最大為17.071 1 N·m、最小為12.803 4 N·m。
從圖4可以看出,當動平臺上負載為0時,驅動電機17、3的輸出力矩雖小但呈遞增的趨勢,說明隨著動平臺偏轉角增加其重力產生的力矩也越大,電機17、3的輸出力矩主要用來克服動平臺及其相關組件重力產生的力矩。
當動平臺上負載為0時,驅動電機17、3的輸出力矩M1、M2雖呈遞增趨勢,但均很小(幾乎為0);由圖7可知,當動平臺在繞X、Y軸方向上同時施加大小相同的負載時,驅動電機17、3均輸出較大的力矩,且M1>M2,故可知平臺自身重力對驅動電機17、3的輸出力矩影響很小,驅動電機輸出的力矩主要用來克服外載。
對比圖5、6可知,當動平臺在繞X軸方向上施加負載、繞Y軸方向上為空載時輸入力矩M1、M2均產生較大的變化;反之當動平臺在繞X軸方向上為空載而繞Y軸方向上施加負載時輸入力矩M2產生較大的變化,M1變化很小,故可知平臺在繞X軸方向上的偏轉不受其繞Y軸負載的影響,而在繞Y軸方向上的偏轉存在耦合關系(受平臺繞X軸負載的影響),與平臺運動學的結論一致,驗證了平臺動力學結論的正確性。
為了驗證所設計平臺的可行性與所建動力學模型的正確性,分別取t=1、3、5、7、9 s時各外載狀態下理論計算值與仿真值進行比較,結果如表1、2所示。

表1 繞X、Y軸空載與均帶載時電機輸出力矩Tab.1 Output torque of motor around X and Y axes under no load and even load N·m
由表1、2可以看出,動平臺9在各種負載狀態下驅動電機17、3輸出力矩M1、M2的理論值與仿真值偏差很小(Δmax=0.010 4 N·m),幾乎相等,驗證了模型的正確性。
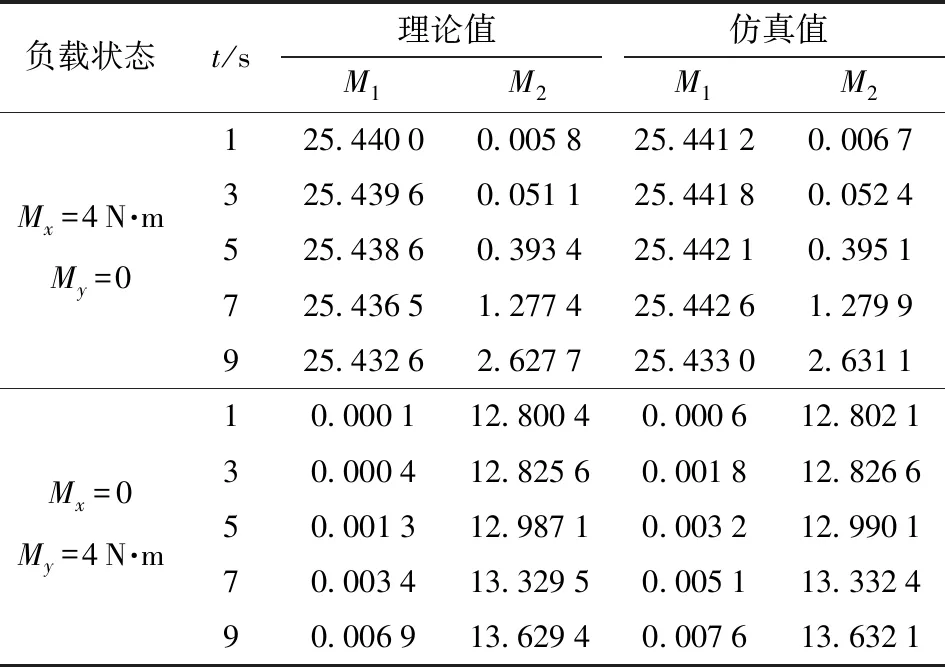
表2 繞X、Y軸分別單獨帶載時電機輸出力矩Tab.2 Motor output torque when X and Y axes were loaded separately N·m
5 結論
(1)所設計的并聯驅動雙向偏轉平臺原理可行,動力學模型正確。
(2)從運動學和動力學分析可知,平臺繞X軸方向上的偏轉不受其繞Y軸方向上偏轉的影響,而繞Y軸方向上的偏轉受其繞X軸方向上偏轉的影響,兩者存在耦合關系。
(3)驅動電機輸出的力矩除了克服由于平臺偏轉零部件重力所產生的轉矩外,主要用來克服外載,這與實際工況相符。

