液力透平幾何參數對壓頭-流量曲線的影響

楊軍虎 馬琦航 羅鈺銅 姬亞亞 林 彬 李之帆

(1.蘭州理工大學能源與動力工程學院， 蘭州 730050； 2.甘肅省流體機械及系統重點實驗室， 蘭州 730050)

0 引言

在化工過程工業中，存在具有高壓能量的液體，利用液力透平可回收這部分高壓液體的能量。然而在實際化工生產中，其產量是根據要求調節，這時生產的流量也會隨之變化，但由于生產工藝的要求其壓力一般保持不變。這就要求液力透平的進出口壓頭隨流量的變化較小，即壓頭-流量曲線比較平坦，以保證生產工藝要求和液力透平機組穩定工作。文獻[1-2]研究泵反轉作液力透平時兩者最優工況下的流量、揚程、壓頭等外特性參數之間的換算關系，以期指導泵作透平的選型問題。文獻[3-4]針對泵反轉作透平時，葉輪葉片的進出口角不符合透平工況，提出了液力透平葉輪葉片進出口角的設計方法，設計了專用的液力透平葉輪，數值模擬和試驗結果表明，液力透平的效率有了一定提高。文獻[5-6]針對葉片包角對液力透平效率的影響進行研究，得出對于每種比轉數的液力透平存在一個最佳的葉片包角，蝸殼斷面為梯形斷面時，液力透平效率最高。文獻[7-8]研究了葉輪幾何參數對離心泵流量-揚程曲線的影響。

本文基于液力透平的理論分析，研究蝸殼、葉輪葉片幾何參數對液力透平壓頭-流量曲線的影響，以期得到蝸殼葉輪幾何參數的影響規律。

1 液力透平的理論分析

1.1 理論壓頭與流量的關系

液力透平中液體流動滿足歐拉方程[9-12]

(1)

式中Hth——液力透平的理論壓頭

u——葉片圓周速度

cu——葉輪進出口圓周速度分量

下標2表示透平葉輪進口，下標1表示透平葉輪出口。葉輪進出口速度三角形如圖1所示。由透平葉輪的進出口速度三角形可得到c2u、c1u，即[13-15]

c2u=c2mcotα2

(2)

c1u=u1-c1mcotβ1

(3)

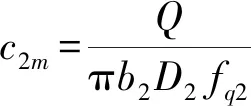
(4)

(5)

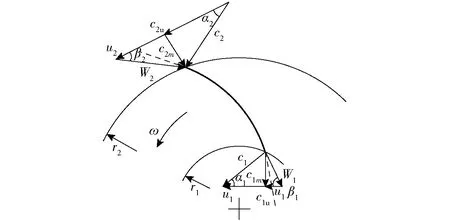
圖1 葉輪進出口速度三角形Fig.1 Speed triangle of impeller inlet and outlet

式中c2m、c1m——葉輪進、出口處軸面速度

α2——葉輪進口絕對液流角

β1——葉輪出口相對液流角

Q——透平進口流量

D2、D1——葉輪進、出口邊直徑

b2、b1——葉輪進、出口邊寬度

fq2、fq1——葉輪進、出口排擠系數

排擠系數計算公式為

(6)

式中Z——葉片數

Su——葉片圓周方向厚度

D——葉輪進、出口邊直徑

葉片圓周速度為

(7)

式中n——葉輪轉速，r/min

將式(2)～(7)代入式(1)中可得

(8)

在液力透平中流體在蝸殼及進入葉輪前按等速度矩規律運動[10]，如圖2所示，c2u計算公式為

c2ur2=K

(9)

式中K——蝸殼常數r2——葉輪進口半徑

(10)

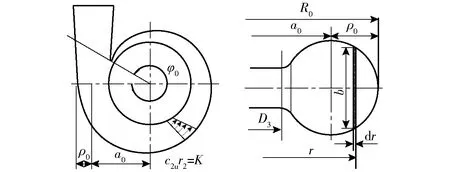
圖2 蝸殼內水流的流動Fig.2 Flow of water in volute

蝸殼常數K的計算與蝸殼截面形狀有關。離心泵蝸殼斷面種類有梯形斷面、圓形斷面、矩形斷面等。不同截面形狀下蝸殼常數計算公式為[10]

(11)

式中φ0——蝸殼包角,(°)

r3——蝸殼基圓半徑

為了方便，研究時取其蝸殼斷面形狀為圓形，圓形斷面如圖2所示。圓形斷面的蝸殼寬度b可表示為所在圓半徑r的函數關系，則蝸殼常數表示為[11]

(12)

式中a0——蝸殼進口斷面與葉輪軸心線的距離

ρ0——蝸殼進口圓斷面半徑

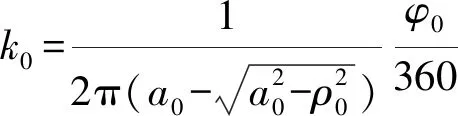
(13)

水流流經蝸殼在葉輪進口處的絕對水流角α2由蝸殼的形狀及幾何參數決定[9,11]，計算公式為

(14)

將式(4)、(13)代入式(14)則有

(15)

將式(6)、(13)、(15)代入式(8)得到液力透平的理論壓頭

(16)

式(16)即為液力透平的理論壓頭隨流量的變化關系，可見透平壓頭隨流量增大而增大，且與葉輪、蝸殼的幾何參數有關。

1.2 透平壓頭-流量曲線的影響因素

為了獲得平坦的透平壓頭-流量曲線，將理論壓頭對流量求導，得出壓頭-流量曲線斜率為

(17)

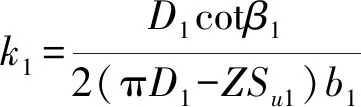
(18)

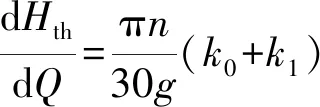
(19)

由式(19)可以看出，透平壓頭-流量曲線斜率變化主要由式(13)和式(18)中的k0、k1決定。由于透平壓頭隨流量增大而增大，斜率大于零。為了使壓頭-流量曲線變平坦需減小k0、k1。k0主要由蝸殼參數確定。設理論壓頭-流量曲線的斜率為hth，即

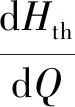
(20)

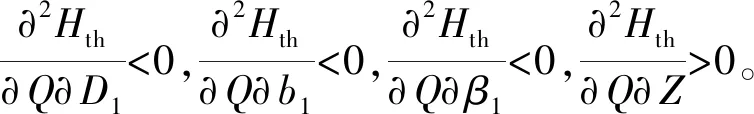
2 透平不同幾何參數的研究方案

2.1 研究對象

選用一臺比轉數為48的單級單吸離心泵反轉作為液力透平研究對象，該泵的設計流量Q=65 m3/h、揚程H=94.37 m、轉速n=2 950 r/min。葉輪葉片為扭曲葉片，表1為該泵葉輪和蝸殼的幾何參數[16-18]。

表1 研究對象主要幾何參數Tab.1 Main parameters of study object

根據表1蝸殼和葉輪幾何參數，用式(13)、(18)計算得到k0=183.1，k1=10.8，可見蝸殼參數對壓頭-流量曲線斜率的影響遠大于葉輪出口處幾何參數。

2.2 數值模擬方案

根據上述分析，在透平葉輪軸面及基本外尺寸和轉速不變的情況下設計數值模擬方案。研究時采用控制變量的方法，在原型泵參數基礎上，改變上述分析得出的幾何參數，在原型泵附近取值，不超過離心泵設計參數取值范圍，其他幾何參數保持不變。將原型泵作透平命名為方案A；改變蝸殼包角為方案B；改變葉輪出口角為方案C；改變透平葉輪出口邊位置和直徑為方案D；改變葉片數為方案E。方案B、C、D、E分別取3個參數變量與方案A作對比，研究壓頭-流量曲線斜率的變化，各方案參數及取值如表2所示。

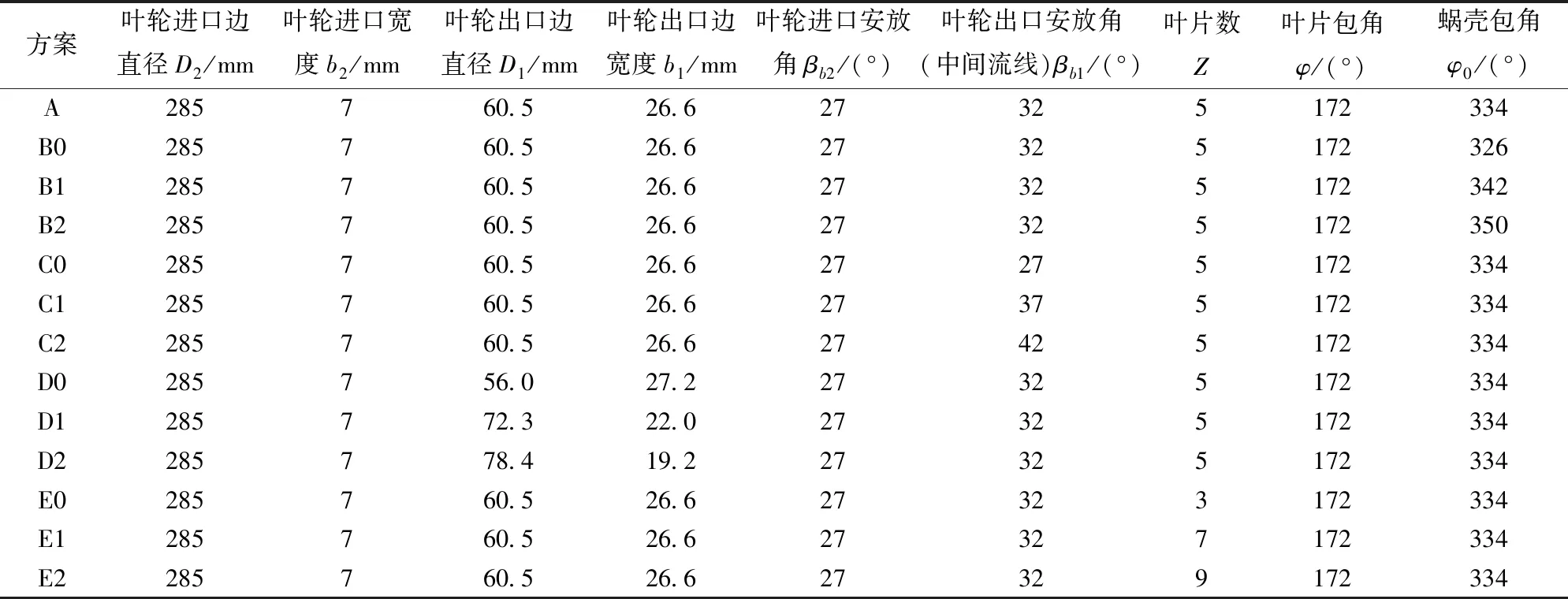
表2 各方案幾何參數Tab.2 Geometric parameters of schemes

2.3 計算模型

按表2中幾何參數建立了葉輪、蝸殼三維模型。方案A模型葉輪與蝸殼如圖3所示。

圖3 液力透平三維模型Fig.3 3D model of hydraulic turbine

2.4 網格無關性檢查

采用四面體進行網格劃分并進行網格無關性檢測，當網格數大于1.2×106時，求得的效率基本保持不變，則網格數量在1.2×106以上合適。A模型的總網格單元數1 254 342，節點數為212 416。其他模型網格數量與該數量相當。

2.5 邊界條件

利用ANSYS-Fluent軟件基于壓力的求解器，透平進口條件為速度進口，出口設為壓力出口，余壓設為0.5 MPa。壓力與速度的耦合方式為SIMPLE算法，計算收斂標準設為10-5，湍流模型采用RNGk-ε湍流模型，輸送介質為常溫清水。通過調節進口速度改變透平的運行工況，然后計算得到不同工況下的性能參數。

3 數值模擬試驗驗證

為了驗證數值模擬的準確性，在液力透平試驗臺上對比轉數為48的原型泵反轉做透平進行試驗，在0.8～2.2倍泵設計工況流量下的8個工況點進行試驗[19-20]，試驗臺如圖4所示。

圖4 液力透平試驗臺Fig.4 Hydraulic turbine test bench

透平效率為輸出功率與輸入功率的比值，即

(21)

其中

Pin=ρgQH

(22)

(23)

式中Pin——透平輸入功率

Pout——透平輸出功率

M——輸出的轉矩

ρ——水密度

將試驗和數值模擬得到的性能曲線繪出，如圖5所示：透平最高效率點為91 m3/h；試驗和數值模擬的壓頭-流量、效率-流量、功率-流量曲線在不同工況點吻合較好，由此可知本文采用數值模擬方法能夠對該臺泵反轉作透平的內部流場進行比較準確的模擬。但試驗得出壓頭略高于數值模擬結果；試驗功率與數值模擬功率相差較小；數值模擬的效率略高于試驗效率；這是由于數值模擬時忽略了軸承和軸封等引起的摩擦損失。

圖5 透平性能數值模擬與試驗對比Fig.5 Comparison between numerical simulation and test of turbine performance

4 結果與分析

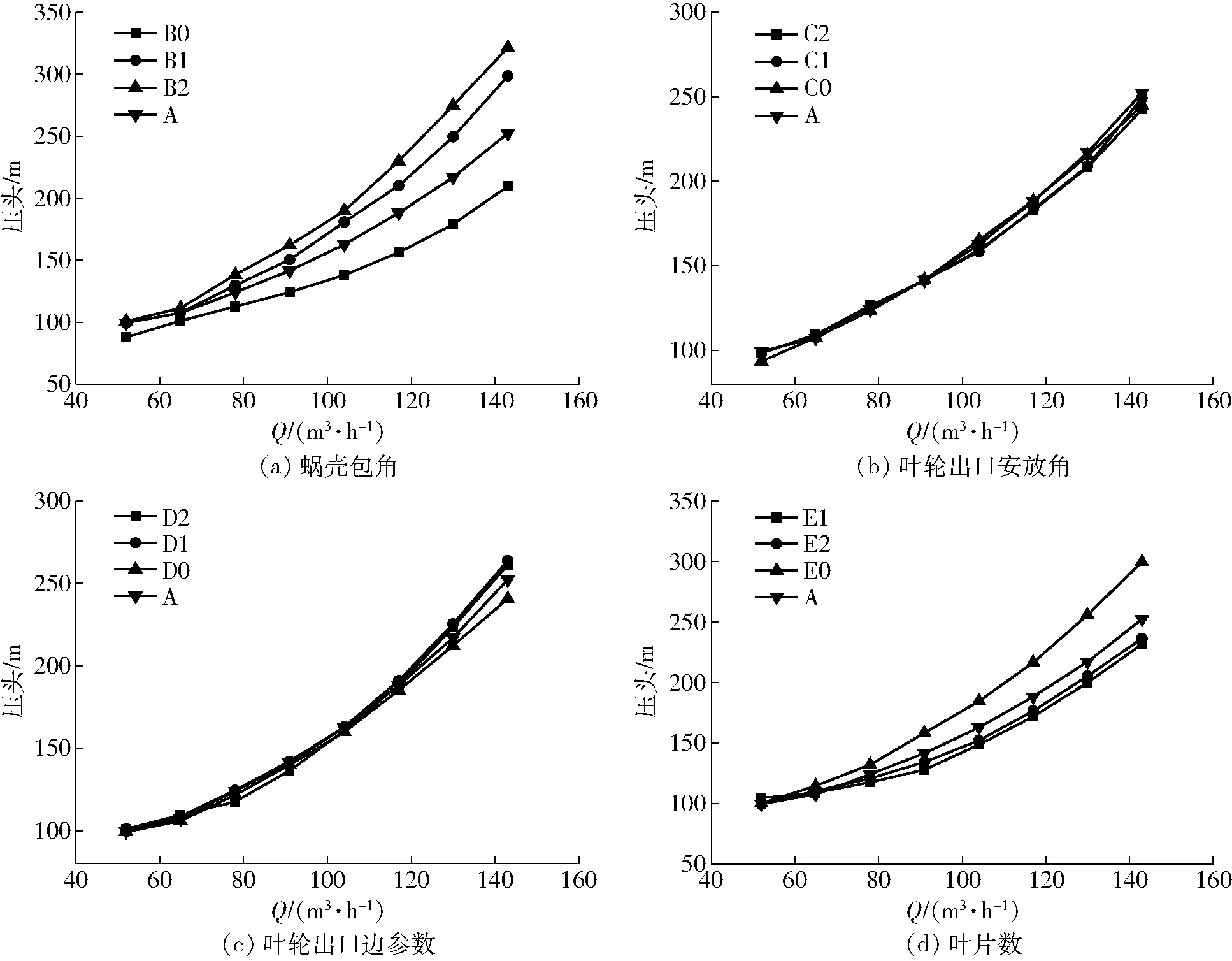
圖6 幾何參數對透平壓頭-流量曲線的影響Fig.6 Effects of geometric parameters on head-flow curves of turbine

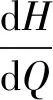
由圖6a和各方案斜率看出，壓頭-流量曲線的斜率隨蝸殼包角變化較大,隨著蝸殼包角的減小壓頭-流量曲線變得平緩，這與理論分析結果一致。也說明適當減小液力透平蝸殼包角能夠使其壓頭-流量曲線變得平坦。

由圖6b和各方案斜率可以得出，隨著透平葉輪出口安放角的增大，壓頭-流量曲線也變得平緩，但其斜率變化不大，符合理論分析結果。

由圖6c和各方案斜率可以看出，在不改變透平葉輪軸面的前提下，透平葉輪出口邊前移，這時出口邊寬度b1減小，平均直徑D1增大，透平的壓頭-流量曲線在1.4QP處斜率隨出口邊位置前移先變大后變小，這說明要使透平壓頭-流量曲線平坦，葉輪出口邊有最佳的出口位置。

由圖6d和各方案斜率可以看出，透平的壓頭-流量曲線在1.4QP處的斜率隨葉片數增多先變小后變大，這說明對于液力透平，存在最佳葉片數可使壓頭-流量曲線平坦，對于研究對象，最佳的葉片數是7個。然而理論分析認為葉片數增多會減小透平壓頭-流量曲線的斜率，這是由于理論分析時沒有考慮葉輪的速度滑移現象，也沒有考慮葉輪內的損失。

5 結論

(1)在蝸殼內速度矩守恒的前提下推導得到了液力透平理論壓頭-流量的關系式；分析得出影響壓頭-流量曲線平坦度的幾何參數為蝸殼包角、葉輪出口安放角、葉輪出口邊參數和葉片數。

(2)研究結果表明：在一定范圍內減小蝸殼包角，增大葉輪出口安放角，會使壓頭-流量曲線變得平坦；存在最佳葉輪出口邊位置和最佳葉片數，可使透平壓頭-流量曲線更加平坦。其中蝸殼包角對壓頭-流量曲線斜率的影響顯著。