4-PRR冗余并聯機構驅動力與能耗優化
胡小亮 謝志江 吳小勇 劉 飛 盧 超 唐小斌
(1.重慶大學機械傳動國家重點實驗室, 重慶 400044; 2.重慶理工大學機械工程學院, 重慶 400054)
0 引言
在某大型連續式跨聲速風洞半柔壁噴管段中,需要設計一種重載3自由度調整機構,調整其中的喉塊段,從而實現對剛柔耦合變形協調、精度控制[1-3]。冗余驅動并聯機構可以提高機構的承載能力與控制精度,獲得較好的剛度特性及動態性能[4-5]。但冗余驅動中驅動數大于自由度數,驅動力與功率分配理論上有無窮多解,需要根據優化目標對其進行優化。
并聯機構的動力學分析可以通過拉格朗日法、牛頓-歐拉法、凱恩法、虛功原理等方法[6-12]得到機構的動力學模型。DONG等[13]采用加權偽逆法優化了驅動力分配,并減小了最大驅動力。NOKLEBY等[14]采用無約束方法對冗余并聯機器人的力旋量能力進行求解,結果表明冗余驅動能夠明顯提升機構的承載能力。王立平等[15-16]采用最小化驅動力的二范數對驅動力進行了優化。卿建喜等[17]提出了最小化驅動器最大瞬時驅動功率和最大瞬時驅動力的優化方法,與非冗余驅動方式相比,冗余驅動能夠顯著降低驅動器的瞬時負載和瞬時輸出功率。LEE等[18-20]利用驅動力二范數及能量矩對2自由度冗余驅動并聯機構進行了能耗優化,結果表明其明顯降低了系統的功耗;文獻[21-22]分析了優化動平臺運動軌跡,表明能減少冗余驅動機構功耗。
本文對平面3自由度4-PRR冗余并聯機構進行運動學與動力學求解,提出驅動力二范數與最小驅動總功率優化方法并對此機構功率進行優化,由驅動功率得到機構運動周期內功耗,與非冗余驅動并聯機構進行對比,得到冗余驅動優化方法的優化特征。
1 機構模型描述與運動學逆解
1.1 機構模型描述
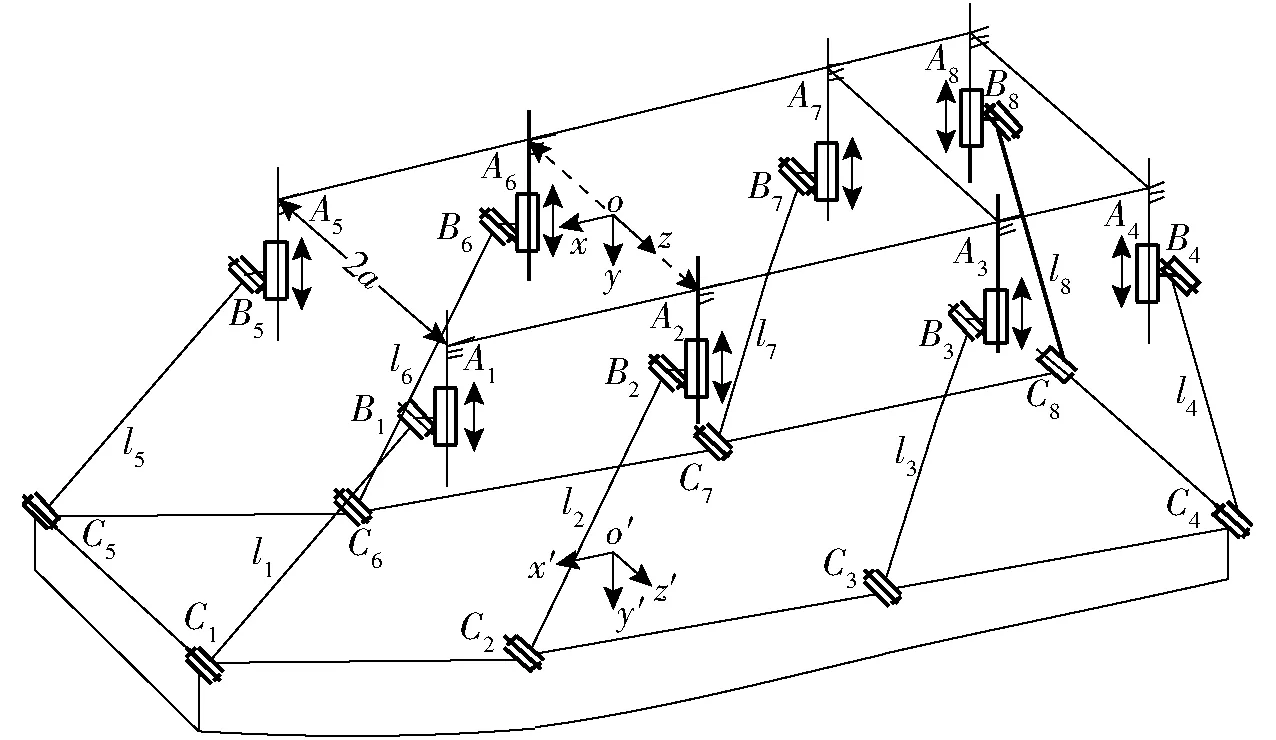
圖1 8-PRR/6-PRR并聯機構結構簡圖Fig.1 Schematic of 8-PRR/6-PRR parallel mechanism
喉塊段驅動實際結構如圖1所示,主要由喉塊、固定基座及連接兩個平臺的拉桿構成。機構共有4組8條運動支鏈,每條分支包含相同的運動部件和運動副,每條支鏈由1個滑塊導軌移動副P和2個轉動副R組成,移動副P為驅動副。將8-PRR冗余驅動并聯機構的第3條和第7條支鏈移除即得到非冗余驅動的6-PRR并聯機構。
由于此機構為1R2T三自由度機構,且關于xoy平面對稱,為便于分析,機構簡化為平面4-PRR冗余驅動并聯機構,如圖2所示。將4-PRR冗余驅動并聯機構的第3條支鏈移除即得到非冗余驅動的3-PRR并聯機構。
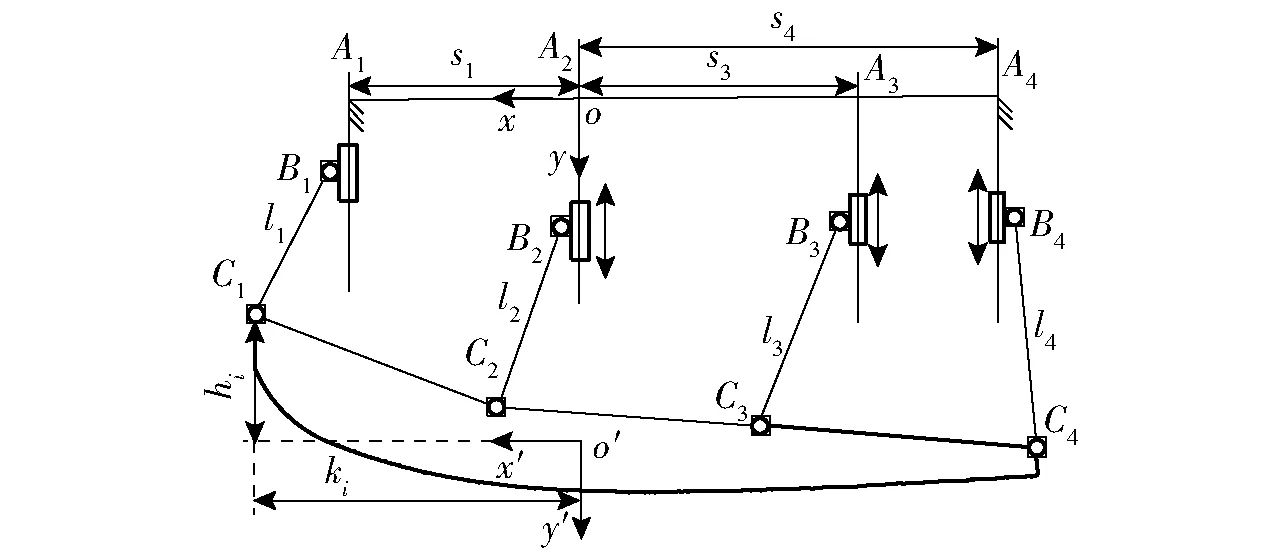
圖2 4-PRR并聯機構結構簡圖Fig.2 Schematic of 4-PRR parallel mechanism
在基座A2建立定坐標系oxyz,在喉塊質心處建立動坐標系o′x′y′z′。各移動副之間的軸線距離為si,拉桿長度為li,下鉸鏈點Ci到平面x′z′的距離為hi, 下鉸鏈點Ci到平面y′z′的距離為ki。其中C1、C2、C3在y′軸的負方向,C4在y′軸的正方向。第i條支鏈的封閉矢量圖如圖3所示。其中,si為移動副軸線在定坐標系中沿x軸的位置矢量,ei為移動副驅動方向單位矢量,ni為上鉸鏈點到移動副軸線的距離矢量,ui為拉桿的單位方向矢量,ci為下鉸鏈點到動坐標系原點的矢量。
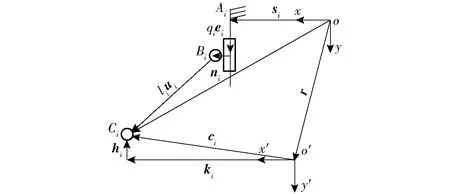
圖3 第i條支鏈封閉矢量圖Fig.3 Vector diagram of the ith PRR kinematic chain
如圖2、3所示,動平臺的位姿可由一個位置矢量r和一個旋轉矩陣oRo′描述。動平臺繞定坐標系z軸旋轉角為θ,則位置矢量r和動坐標系相對于參考坐標系的旋轉矩陣oRo′分別為
(1)
(2)
1.2 運動學求解
平面4-PRR冗余驅動并聯機構和3-PRR并聯機構的運動學求解方法相同,本節以4-PRR關聯機構為模型進行求解。
1.2.1位置逆解
如圖3所示,建立位置封閉矢量方程
(3)
則該機構的位置逆解模型為
(4)
將已知結構參數條件代入式(4),得到4條驅動支鏈的位置逆解表達式為
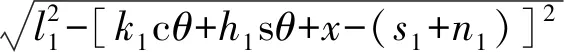
(5)
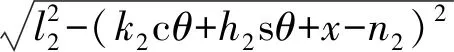
(6)

(7)
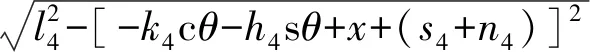
(8)
其中sθ表示sinθ,cθ表示cosθ。
1.2.2雅可比矩陣及速度求解
求解并聯機構的雅可比矩陣一般使用微分變換法或者矢量積法。針對該冗余并聯機構采用基于符號運算的微分變換法,求出一階影響系數矩陣,并采用一階運動影響系數對該機構速度雅可比矩陣快速求解。
滑塊位置可以表示為
(9)
將式(9)對時間求導,得到滑塊速度為
(10)
即得到該機構末端速度與驅動速度的映射關系為
(11)
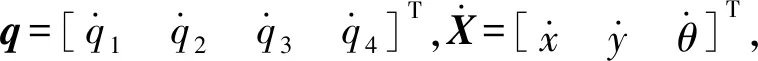
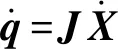
(12)
其中


J——雅可比矩陣,機構的一階影響系數矩陣
對于3-PRR并聯機構,雅可比矩陣為3×3的方陣。
1.2.3加速度求解
機構運動影響系數反映了機構的運動學和動力學本質。本文利用機構的二階運動影響系數求解滑塊加速度。
將式(10)對時間求導表示為
(13)
式中Hi——二階影響系數矩陣

由式(13)求解得驅動加速度
(14)
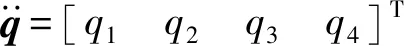
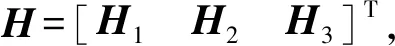
2 動力學建模
動力學建模方法主要包括牛頓-歐拉法、凱恩法、拉格朗日功能平衡法以及虛功原理法。虛功原理建模方法在執行效率和算法上更為出色。本文采用虛功原理進行冗余并聯機構及其非冗余并聯機構的動力學模型建模。由于拉桿的質量相對于動平臺、滑塊及推桿的質量較小,轉動慣量也較小,把拉桿質量轉換到動平臺和滑塊質量上。
動平臺在風洞流場中做平面運動,為便于分析,將其擴展到空間運動。對于動平臺,外力、慣性力和重力合力為
(15)
式中mp——動平臺、下鉸鏈及每根拉桿一半質量的質量和
fe——作用于動平臺的外力
ne——作用于動平臺的外力矩
wp——動平臺角速度

oIp——動平臺在定坐標系下的慣性張量
對支鏈i的滑塊及推桿,只有平動,則作用在滑塊上的驅動力、慣性力和重力合力為
(16)
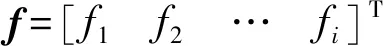
式中mqi——第i條支鏈上滑塊、推桿、上鉸鏈及一半拉桿的質量和
N——滑塊慣性力
Ni——第i條支鏈上的慣性力
f——滑塊驅動力
fi——第i條支鏈上的驅動力
由式(15)、(16)可得,虛功原理可描述為
(17)
其中
δxp=[δxpδypδθp]T
式中 δxp——動平臺虛位移
δq——驅動虛位移
式(17)中,虛位移δxp與δq滿足機構關節的約束,其關系為
δq=Jδxp
(18)
將式(18)代入式(17)得
(19)
式(19)對任意的δxp均成立,因此有
Fp+JTf+JTN=0
(20)
其中
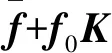
(21)
(JT)+=J(JTJ)-1
f0=(E-(JT)+JT)
式中 (JT)+——JT的廣義逆矩陣
f0——JT的零空間基向量
K——JT的零空間基向量系數
E——單位矩陣
對于3-PRR非冗余并聯機構,(JT)+為JT的逆矩陣,f0不存在。對于4-PRR冗余并聯機構,式(21)有4個未知數、3個線性方程,故解不是唯一的;對于3-PRR非冗余并聯機構,解是唯一的。
3 驅動輸入功率分析
對3-PRR非冗余并聯機構的輸入功率進行分析;并利用驅動力的二范數解、周期內功耗最小兩種方法分別對4-PRR冗余并聯機構的輸入力、功率進行優化分析。
3.1 3-PRR非冗余并聯機構驅動功率
對于3-PRR非冗余并聯機構,其輸入驅動力和驅動功率為
f=-(JT)-(Fp+JTN)
(22)

(23)
其中
3.2 4-PRR冗余并聯機構驅動功率
對于4-PRR冗余并聯機構,分別利用驅動力的二范數解和最小驅動總功率兩種方法求解。
3.2.1驅動力二范數解
對該冗余并聯機構,驅動力配置方式有無窮多種,利用驅動力二范數解,式(21)可寫為
f=-(JT)+(Fp+JTN)
(24)
驅動功率

(25)
其中
即為4-PRR冗余驅動并聯機構驅動力二范數解得的驅動器輸出功率。
3.2.2最小驅動總功率解
由式(21)可得,驅動功率為
(26)
其中
對于第i個驅動器,雖然輸出功率在一個周期內有正負,其輸出功總是正的,故在由功率對時間在一個周期內積分時,應該對功率取絕對值,即
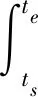
(27)
式中ts——開始時間te——結束時間
則,一個周期驅動器總的輸出功
由式(26)可知,瞬時輸出功率解不唯一,為使一個周期內輸出功最少,則瞬時輸出總功率應該最小,瞬時輸出總功率為
Ps=|P1|+|P2|+|P3|+|P4|
(28)
其中,Ps為關于零空間系數K的非線性函數。當Ps取得最小值時,將K代入式(21)、(26)即得到驅動器瞬時輸出總功率最小時的驅動力與輸出功率。
對每個驅動器,其輸出功率最大不能超過其額定功率,利用Matlab中的工具箱文件fmincon求解有約束的非線性最小值Psmin。通過得到有限個時間點的最小功率來逼近理論上的最小功率變化。其將t時刻的基向量系數返回值kj作為t+Δt時刻的初值循環求解Psmin,流程如圖4所示。
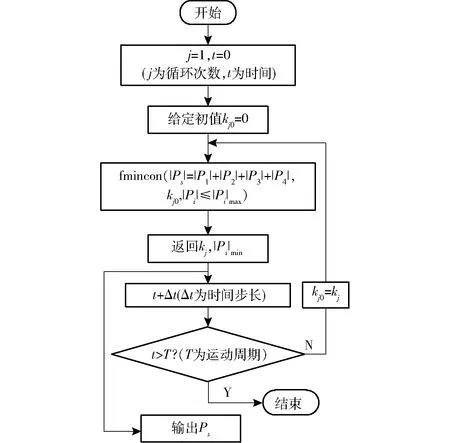
圖4 最小功率變化仿真流程Fig.4 Flow chart of minimum power’s simulation
3.3 周期內驅動器輸出功
對冗余和非冗余并聯機構,驅動器總的輸出功率為
Ps=|P1|+|P2|+…+|Pi| (i=3或4)
(29)
則一個周期內總的輸出功為
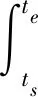
(30)
一個周期內驅動器輸出功率W近似求解計算方法為
(31)
其中
式中n——時間間隔數
tk——一個時間間隔的起始時刻
tk+1——一個時間間隔的結束時刻
4 數值模擬分析
綜合分析風洞試驗條件及并聯機構的實際要求,該并聯機構參數如表1所示。

表1 并聯機構結構參數Tab.1 Geometrical parameters of parallel manipulator
動平臺的質量為12 547.33 kg,其在動坐標系中的慣性張量矩陣為
其在定坐標系中的慣性張量為
oIp=oRo′o′Ipo′Ro
在動坐標系中,作用于動平臺的外力為
則在定坐標系中外力為
根據該并聯機構在風洞中的狀況,選擇一種典型工況進行剛體動力學與能耗分析,其運動軌跡為

由式(11)和式(13)得到滑塊速度與加速度曲線如圖5、6所示。
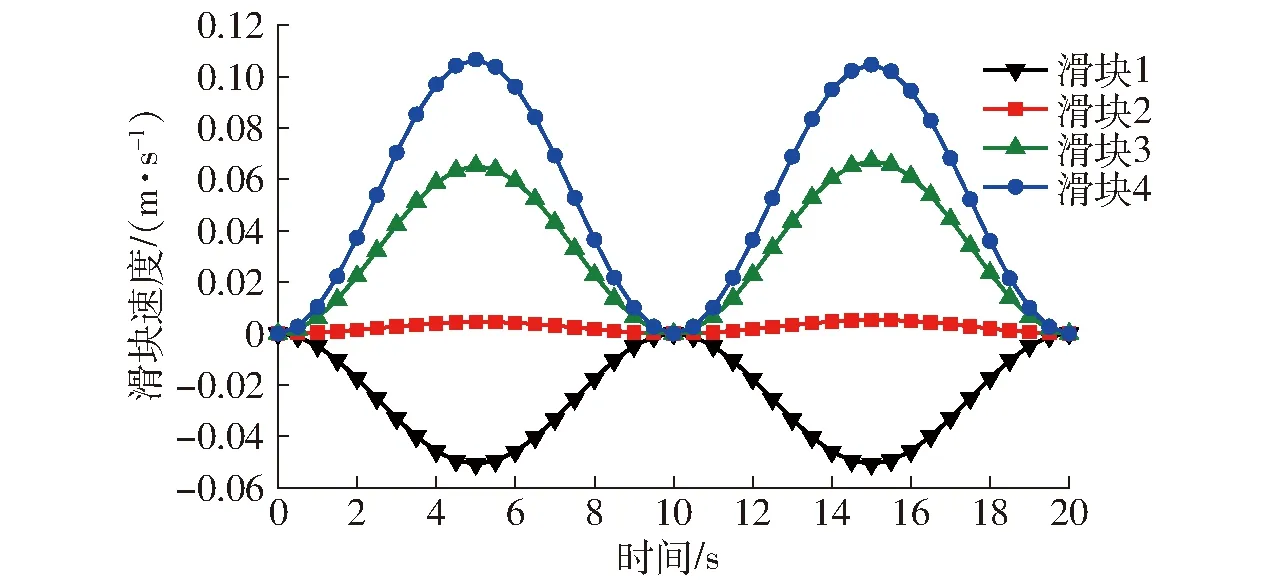
圖5 滑塊速度曲線Fig.5 Velocity curves of sliders
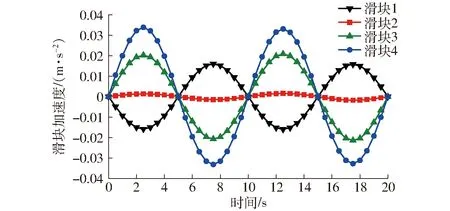
圖6 滑塊加速度曲線Fig.6 Acceleration curves of sliders
由圖5和圖6可得,機構最大速度和加速度都出現在滑塊4,分別為0.107 m/s和0.033 9 m/s2,即最大位移也出現在滑塊4。

圖7 驅動力仿真結果Fig.7 Simulation results of driving forces
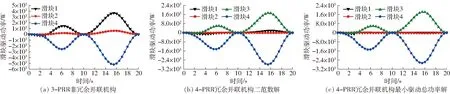
圖8 驅動功率仿真結果Fig.8 Simulation results of driving power
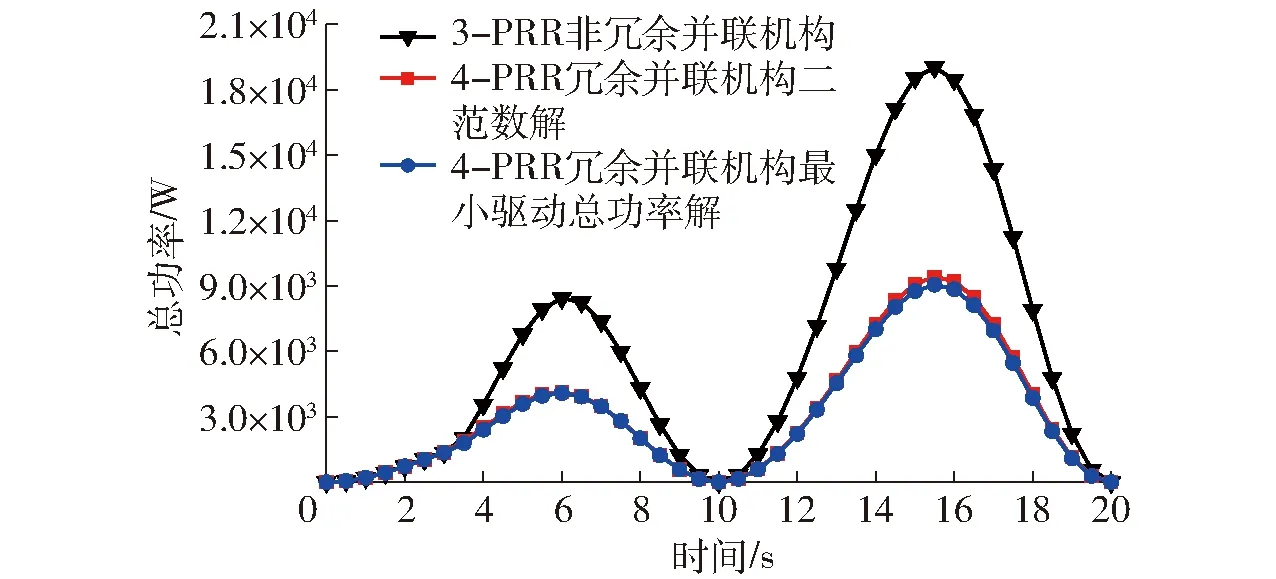
圖9 總功率仿真結果Fig.9 Simulation results of sum of driving power
由式(22)、(24)、(21)得到驅動力仿真結果如圖7所示。由式(23)、(25)、(26)得到驅動功率仿真結果如圖8所示。由式(31)可得,非冗余并聯機構、冗余并聯機構驅動力二范數解和冗余并聯機構最小驅動總功率解在一個周期內的驅動器輸出總功率及總功分別如圖9和表2所示。
對于3-PRR并聯機構對應的6-PRR并聯機構,總功為6個驅動器做功之和;對于4-PRR并聯機構對應的8-PRR并聯機構,總功為8個驅動器做功之和。

表2 驅動器輸出總功Tab.2 Total output power of driver J
從圖7可看出,在運動周期內,3-PRR并聯機構最大驅動力出現在滑塊2,最大驅動力為145.1 kN。由驅動力二范數解和最小驅動總功率解得到的4-PRR冗余驅動并聯機構最大驅動力相比于3-PRR并聯機構最大驅動力都明顯減小,4-PRR冗余驅動并聯機構驅動力二范數解最大驅動力出現在滑塊3,為33.4 kN;4-PRR冗余驅動并聯機構最小驅動總功率解最大驅動力出現在滑塊3,為35.6 kN。4-PRR冗余驅動并聯機構滑塊3和滑塊4起主導作用,兩者的驅動力明顯大于滑塊1和滑塊2;4-PRR冗余驅動并聯機構最小驅動總功率解存在異常驅動,在3.5~20 s內,僅電機2、3、4起到驅動作用,其產生的原因是4-PRR冗余驅動并聯機構的功耗被作為優化模型,并且該優化模型僅與功率的絕對值有關,即為驅動力的絕對值函數。
從圖8可以看出,在運動周期內,3-PRR并聯機構最大驅動功率出現在滑塊4的15.5 s處,為-5 200.9 W(負功);冗余驅動并聯機構最大驅動功率明顯減小,4-PRR冗余驅動并聯機構驅動力二范數解最大驅動功率出現在滑塊4,為-2 788.5 W(負功);4-PRR冗余驅動并聯機構最小驅動總功率解最大驅動功率出現在滑塊4,為-2 665.4 W(負功)。冗余驅動滑塊3和滑塊4的驅動功率遠大于滑塊1和滑塊2的驅動功率。
由圖9和表2可知,冗余驅動并聯機構電機輸出總功明顯減少,分別減少到64 232 J和62 321 J,分別減少49.2%和50.7%;4-PRR冗余驅動并聯機構最小驅動總功率解做功略小于驅動力二范數解做功。
5 結論
(1)建立了4-PRR冗余并聯機構及其非冗余3-PRR并聯機構的運動學逆解模型,根據坐標變換和結構特點得到運動學逆解和機構雅可比矩陣,利用二階影響系數法求解了加速度模型,為動力學分析提供了基礎。
(2)利用虛功原理構建了機構動力學模型,提出以并聯機構運動周期內驅動器做功為優化目標,求解了3-PRR非冗余并聯機構及其4-PRR冗余并聯機構驅動力二范數解、最小驅動總功率解的滑塊驅動力和和驅動功率。
(3)冗余驅動并聯機構能夠有效減少運動周期內驅動器做功,其中驅動力二范數解與最小驅動總功率解的驅動器做功差異較小,且驅動力二范數解不存在驅動奇異,故能夠在均衡驅動力上有效減少驅動器做功。
(4)冗余并聯機構與非冗余并聯機構的驅動力與功率仿真結果表明,驅動力二范數解與最小驅動總功率解所做總功分別減少49.2%和50.7%。

