基于未來效率的兼顧公平與效率的資源分配DEA模型研究
——以各省碳排放額分配為例

王 熒,王應明

(1.福建江夏學院金融學院，福建 福州 350108；2.福州大學經濟與管理學院，福建 福州 350108)

1 引言

評估各生產決策單位(Decision Making Unit，DMU)的投入產出效率及改進潛力，可以為經濟分析、管理決策提供重要參考。Farrell[1]在1957年首創了現代效率的測度技術：首先，構建DMU的生產前沿面，其次，測算DMU的實際投入產出點順著某一路徑改進至生產前沿面的距離作為的該DMU的效率改進空間。該測算技術的前提是要獲知DMU的生產前沿面。Farrell[1]認為可以使用兩種方法來構建生產前沿面：參數型模型法和非參數的數據包絡法(Data Envelopment Analysis， DEA)。

在提出之后，非參數的DEA方法沒有馬上得到多數學者的認可。直到1978年，Charnes等[2]提出的不變規模報酬模式下的CCR模型，DEA方法才得到學術界普遍關注。隨后，Banker等[3]提出生產規模收益可變的BCC模型。迄今為止，CCR模型和BCC模型是應用最廣泛的傳統DEA模型。不過，CCR模型和BCC模型均假設產出僅為期望產出，忽略了現實經濟中，除了期望產出外，產出往往還包括廢水、廢氣、固廢等非期望產出。因此，需要對傳統DEA模型進行拓展。現有文獻主要提出三種思路解決非期望產出[4-6]：(1)將非期望產出當作投入處理[4-5]。(2)以“非對稱”方式處理各種產出，例如，采用曲線測度法[6]、方向距離函數法[7]、多階段DEA模型[8-9]、SBM模型[10]等方法模型，實現增加期望產出的同時，減少非期望產出。(3)數據轉換函數法[11]，例如，采用取倒數等數學變換法，人為地將越小越好的非期望產出轉換成越大越好的“期望產出”。

DEA方法可以得到與經典的邊際分析完全相似的結論[12]。因此，近年來，許多文獻將DEA方法的應用從效率評價拓展到資源分配。現有文獻中，資源分配的DEA模型主要有四種:(1)固定成本分配的DEA模型[13-15]。(2)中央化資源分配的DEA模型[16]。(2)零和博弈DEA模型[17]。(4)資源配置的參數DEA模型，包括了HFM-DEA模型[18]、SFM-DE模型[19]、ASFM-DEA模型[20]、EFM-DEA模型[21]等。

總體而言，對于效率評價和資源分配的DEA模型的研究，現有文獻已經取得了不少成果，但也還存在一些問題需要進一步解決。

首先，現有DEA模型大都根據以往的數據，對各DMU進行效率評價，并在此基礎上進行資源分配。但是，過去的DEA效率并不代表未來時期的DEA效率。假設，當前時間為第t期，現在需要分配未來第t+1期的資源，根據經濟學原理，應該要根據各DMU第t+1期的效率進行分配，才能實現第t+1期的最優資源分配。為此，本研究首先根據歷史數據計算每個生產決策單元過去各期的技術增長率，并預測各DMU未來的技術增長率，進而獲得未來的生產前沿面和生產可能性區域，從而為下文的基于未來效率的資源分配的DEA模型奠定基礎。

其次，現有的DEA模型，大都通過使各DMU移動到生產前沿面，從而實現最優的效率和資源分配[22]。然而，這樣的效率評估與資源分配顯得相對狹隘，對于實際的管理運用也相對有限。因為，現實經濟中，管理往往都是為了實現一定的期望目標，因此，管理者更希望評估各DMU的實際投入產出距離期望目標還有多大的效率改進空間，在此基礎上進行資源分配。Lozano等[16]構建資源分配的DEA模型，實現了一定程度的多目標導向的資源分配：該DEA模型涉及的目標包括最大化總的期望產出、最小化總的可變要素投入和最小化總的非期望產出等三個，管理者可以調整三個目標的優先順序進而形成不同的資源分配方案。盡管如此，在現實管理中，該DEA模型依然難以滿足管理者的各種目標追求。因為，現實中，管理者未必總是希望每個子目標都要實現最優化，而是希望某些子目標實現一定程度優化的基礎上，使另外一些子目標實現最優化，例如，管理者可能希望總的可變要素、總的非期望產出實現一定程度的縮減下實現總的期望產出的最大增長和最優配置。另一方面，管理者追求的目標往往是比較復雜的多目標——不只追求經濟技術上的最優，而且往往也要兼顧諸如社會公平等目標。為此，本研究參考Lozano等[16]提出的DEA模型，基于測算出的未來的生產前沿面，構建了基于未來效率的兼顧公平與效率的資源分配的DEA模型。

該模型賦予管理者充分的靈活度來預先設定各種目標，具體包括九個硬性目標和三個軟性目標。其中，硬性目標是指必須要滿足的目標，三個針對各DMU的投入產出、三個針對全部DMU的投入產出總量、三個針對各種投入產出分配公平，這九個硬性目標均可以按照管理者的期望設定不同的值。在九個硬性目標約束下，分三個階段分別實現三個軟性目標：最大化期望總產出、最小化非期望總產出、最小化要素投入。管理者不僅可以改變九個硬性目標的參數值，以及調整三個軟性目標的優先順序，而且還可以在每個步驟潛力評估的基礎上，根據節能減排潛力通過改變三個軟性目標參數，進一步設定合理的期望目標，從而形成各種目標導向的兼顧效率與公平的資源分配方案。最后，本研究將構建的DEA模型運用于我國各省碳排放額分配研究。

2 變量及生產可能性區域假設

資源分配問題可以描述為：要在生產可能性區間內和目標約束下，合理分配資源，進而盡可能實現管理者期望的目標。為了構建基于未來效率的資源分配的DEA模型，需要對模型中涉及的變量以及DEA模型的生產可能性區域的假設進行說明。

2.1 變量說明

假設，共有J個DMU，每個DMU的投入產出種類相同，即，有I種要素投入，其中，IF種為固定要素，I-IF種為可變要素；共有K+S種產出，其中，K種為期望產出，S種為非期望產出，其他相關變量的名稱與含義具體見表1。

表1 相關變量的名稱與含義

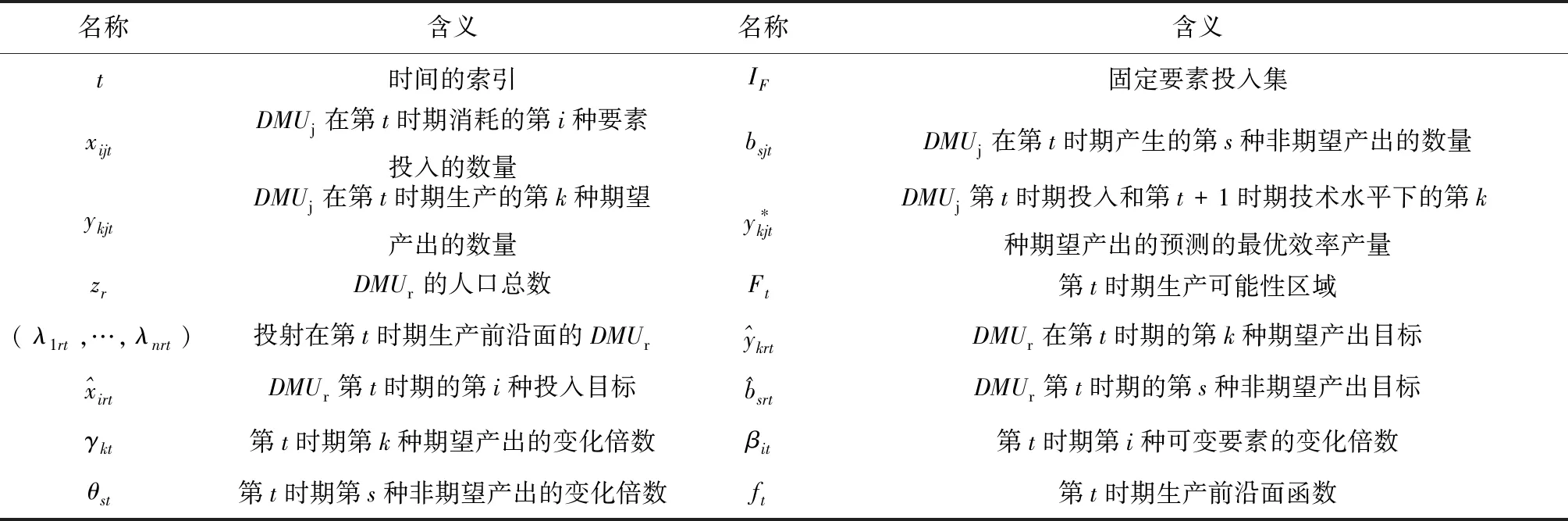
續表1 相關變量的名稱與含義

2.2 生產可能性區域的特征假設

參考Adler和Volta[4]的研究，本文中的生產可能性區域的假設包括以下幾個方面：

Ⅰxijt≥0,ykjt≥0,bsjt≥0 (?i?k?s?t)；

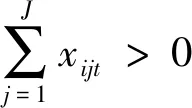
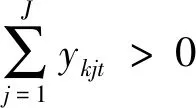
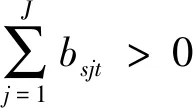
Ⅵ (ykjt,bsjt)∈Ft(Xt,Yt,Bt)?(θykjt,θbsjt)∈Ft(Xt,Yt,Bt)forall0≤θ≤1(?t)；

Ⅶ (ykt,bst)∈Ft(Xt,Yt,Bt),yk′t≤ykt?(yk′t,ykb)∈Ft(Xt,Yt,Bt)(?t)；

Ⅷλj≤1 ?j。

其中，(Ⅰ)式的含義是：任何DMU的任何投入產出均不能小于零；(Ⅱ—Ⅳ)式的含義分別是：任何一種要素(產出)都至少被一個DMU使用(生產)，任何一個DMU都至少使用一種要素，都至少生產一種期望產出和一種非期望產出；(Ⅴ)的含義是：要沒有非期望產出，則也沒有期望產出，即，期望產出和非期望產出具有聯合生產的性質；(Ⅵ)式的含義是：非期望產出具有弱可自由處理性；(Ⅶ)的含義是：期望產出具有強可自由處理性；(Ⅷ)規模收益可變。根據Kuosmanen[23]，同時滿足(Ⅰ—Ⅷ)的生產可能性集合可以描述為以下的線性方程組(1)。

Ft=

(1)

3 未來效率的資源分配的DEA模型構建

3.1 構建總體思路

表2 模型中的硬性目標參數的名稱與含義

3.2 基于未來效率的資源分配的DEA模型

3.2.1 目標參數說明

模型涉及的目標包括硬性目標和軟性目標，具體參數的名稱與含義見表2。其中，硬性目標是指必須要滿足的目標，共有九個：三個是針對各DMU、三個是針對全部DMU的整體、三個是針對各種投入產出分配公平，這九個硬性目標均可以按照管理者的期望設定不同的值。不同公平原則，會有不同的公平含義與目標約束式，本文的公平原則：要盡可能使各DMU的各種投入(產出)的人均量都相等，均等于全國總的人均量。因此，本研究三個反映公平目標的約束式——使得各DMU的人均可變要素、人均期望產出和人均非期望產出與公平合理的人均量的偏離控制在合理的范圍內。軟性目標為盡量要實現的目標，共有三個：產出目標、節能目標和減排目標，每個軟性目標都可以通過構建一個DEA模型予以實現。

3.2.2 基于未來效率的資源分配的DEA模型的構建

假設管理者的目標為：未來時期內，在管理者設定的硬性目標以及實現一定節能、減排目標前提下，最大化期望產出。可以通過構建模型(2)、模型(3)和模型(4)來實現這樣目標追求下的資源分配。

第一階段的模型(2)，主要用來評估未來效率和硬性目標約束下的總可變要素投入的節約潛力。模型(2)中，(2.1)—(2.2)為節能軟性目標式；(2.3)—(2.6)為生產可能性集；(2.7)—(2.15)為硬性目標約束式。其中，(2.7)—(2.9)分別要求未來時期每個DMU的各種要素投入、各種期望產出和各種非期望產出均在管理者設定的范圍內；(2.10)—(2.12)分別要求未來時期全部DMU的各種要素投入、各種期望產出和各種非期望產出控制在在管理者希望的范圍內；(2.13)—(2.15)分別要求未來時期每一個DMU的分配公平狀態控制在在管理者希望的范圍內。由此可見，模型(2)評估了：未來時期，在九個硬性目標下，可變要素投入總量的最大節能潛力。

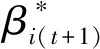
第二階段的模型(3)，主要評估了未來時期內非期望產出的削減潛力: 與模型(2)相比，模型(3)有兩處不一樣：第一，(3.1)—(3.2)為減排軟性目標式；第二，多了限制條件(3.16)：未來時期，每種可變要素總量都實現管理者希望的最小縮減目標。

(2.1)

(2.2)

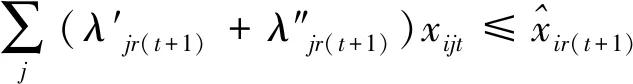
(2.3)

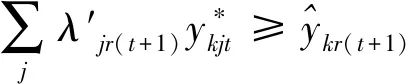
(2.4)

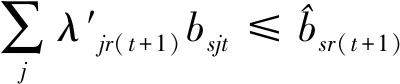
(2.5)

(2.6)

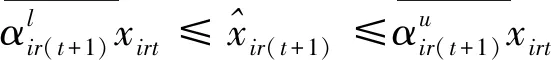
(2.7)

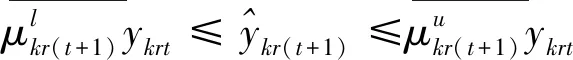
(2.8)

(2.9)

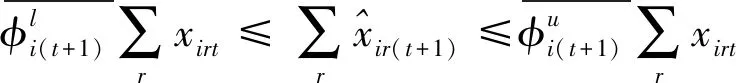
(2.10)

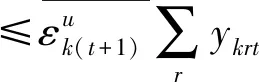
(2.11)

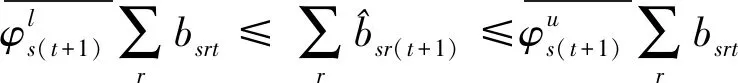
(2.12)

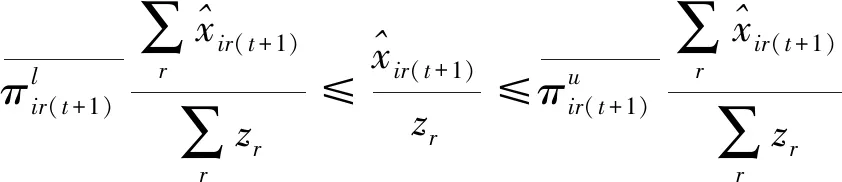
(2.13)

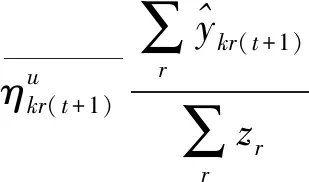
(2.14)

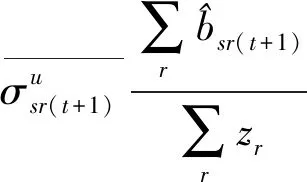
(2.15)

(?i?j?k?s?r)

(3.1)

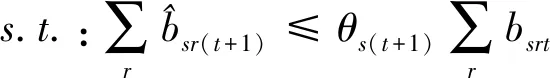
(3.2)

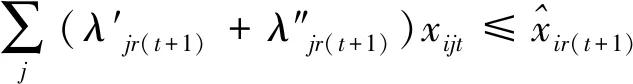
(3.3)

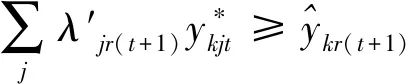
(3.4)

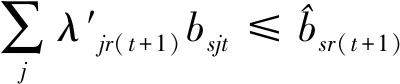
(3.5)

(3.6)

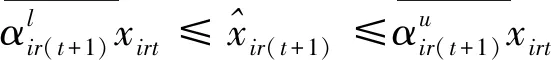
(3.7)

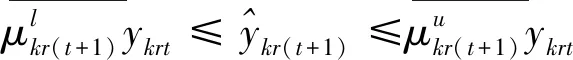
(3.8)

(3.9)

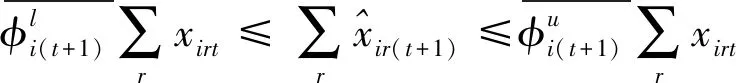
(3.10)

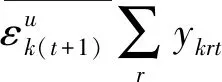
(3.11)

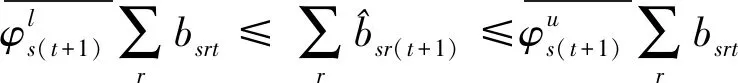
(3.12)

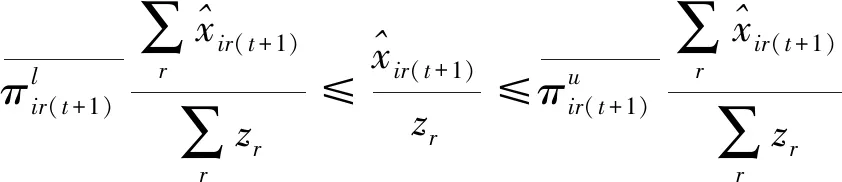
(3.13)

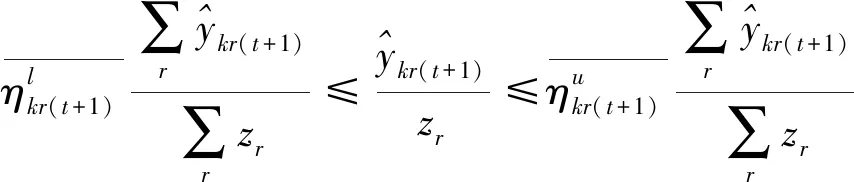
(3.14)

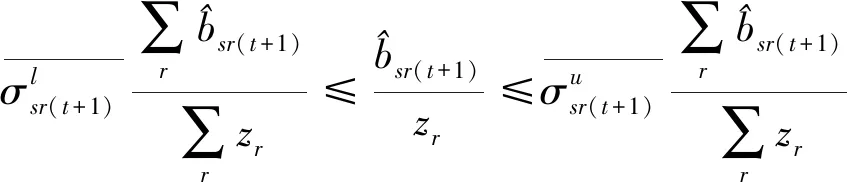
(3.15)

(3.16)

≥0 (?i?j?k?s?r)

(4.1)

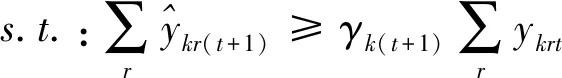
(4.2)

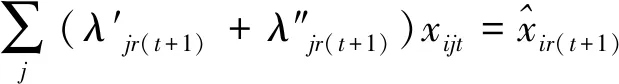
(4.3)

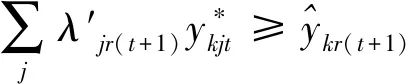
(4.4)

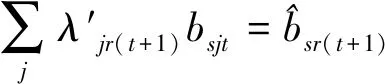
(4.5)

(4.6)

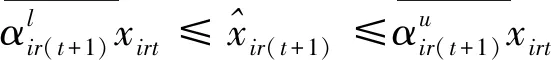
(4.7)

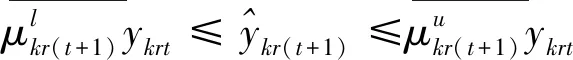
(4.8)

(4.9)

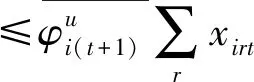
(4.10)

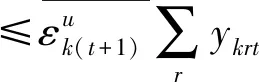
(4.11)

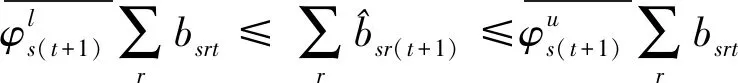
(4.12)

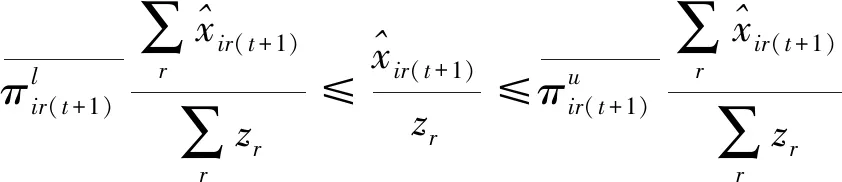
(4.13)

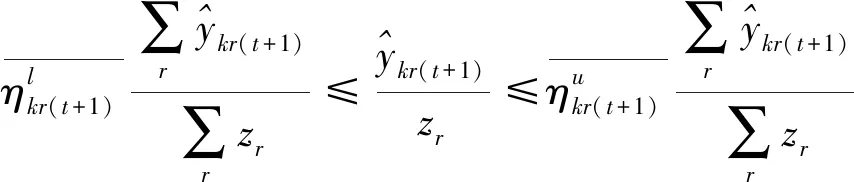
(4.14)

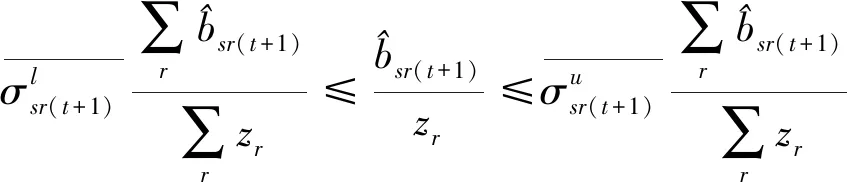
(4.15)

(4.16)

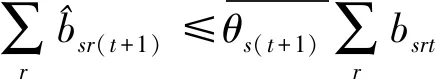
(4.17)

≥0 (?i?j?k?s?r)

第三階段：通過構建模型(4)，實現在管理者設定的硬性約束、總量上實現一定程度的節能減排等前提下總的期望產出最大化的目標。與模型(3)相比，模型(4)有兩處不一樣：第一，(4.1)—(4.2)為產出軟性目標式；第二，多了限制條件(4.17)：未來時期，每種非期望產出總量都縮減至設定的最小縮減目標。

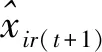
4 實證分析

4.1 實證思路

每個省區當作一個DMU。每個DMU的要素包括勞動投入、能源投入和資本投入等三種，分別用i=1、2、3作為其索引，其中，資本投入為固定要素；期望產出為GDP一種，用k=1作為其索引；非期望產出為廢水排放總量、固體廢棄物總量、碳排放總量等三種，分別用s=1、2、3作為其索引。由于數據的可得性，本研究將四川省和重慶市合并成未進行行政劃分前的四川省，同時沒有將西藏自治區、香港特別行政區、澳門特別行政區以及臺灣省納入分析，即，本研究的實證分析主要包含29個省區。

本研究將采集29個省區所有七個投入產出指標的2000年至2015年的數據，運用構建的基于未來效率的資源分配的DEA模型對我國各省的碳排放額進行分配。

4.2 數據說明

第一，勞動投入。由于我國缺乏平均工作時間的統計數據，因此，本研究以2001年至2016年的各省《統計年鑒》中公布的當年“就業人數”作為各省勞動投入數據。

第二，能源投入。除了2013年以外，采集2001年至2016年的《中國能源統計年鑒》中的“分地區能源消費總量”一值作為各省相應年度的能源投入。其中，2013年的數據采集自各省統計年鑒的“能源消費總量”一值。

第三，資本投入。運用“永續盤存法”[25]估算各省各年份資本存量。計算中所需數據來源與參數設定情況：資本折舊率取值為0.4[25]；采用張軍等[25]測算的各省區2000年的資本存量作為初始資本存量；各年份各省固定資本形成額數據來自各年份的《中國統計年鑒》，并用固定資產投資價格指數折算成以2000年為基期的不變價格的數據。

第四，GDP。各省各年份的數據采集自各年的《中國統計年鑒》，利用平減指數折算成2000年為基年的不變價格的GDP。

第五，廢水排放總量，采集自2001年至2016年《中國統計年鑒》。

第六，固體廢棄物總量，采集自2001年至2016年《中國統計年鑒》。

第七，碳排放量。根據IPCC的《國家溫室氣體清單指南第二卷(能源)》第六章的估算公式來計算碳排放量。估算所需的參數設定以及數據來源情況：各種化石能源的能源凈發熱值的數據來源于《中國能源統計年鑒2013》附錄4；根據IPCC的《國家溫室氣體清單指南第二卷(能源)》的表1.3設定各種化石能源的碳排放因子；將煙煤和無煙煤的碳排放因子按照8∶2的權重加權平均得到煤炭的碳排放因子，碳氧化因子設置為1；采用各省電能凈消費量(電能消費量-電能生產量)來估算各省電能消費產生的碳排放量，同時，按照我國火力發電占比(78.05%)的折算比例將電能折算成標準煤(折算系數為0.1229千克標準煤/千瓦小時)，最后，根據每千克標準煤排放2.763千克二氧化碳的標準，估算出各省電能凈消費導致的碳排放量。

4.3 預測方法的選擇

基于每個省僅有15年的有限樣本數據的事實，本研究擬通過比較分析，在指數平滑法、灰色預測法和ARIMA模型等三種適合小樣本數據的預測方法中選一種用于測算各省區2001年至2016年各年的技術增長率。經過模式識別和檢驗，發現ARIMA模型為ARIMA(0，0，0)，即，實際上ARIMA模型用平均值作為預測值，效果較差，因此，本研究主要在指數平滑法和灰色預測法中進行選擇。

通過表3的比較可以看出，指數平滑法的總平均相對誤差為1.99%小于灰色預測法的2.41%。因此，本研究選擇指數平滑法作為未來技術增長率的預測方法。

表3 主要預測方法預測各省技術增長率的相對誤差比較

根據表3，運用指數平滑法預測各省技術增長率的平均相對誤差都較小，其中，最大的是甘肅省，其平均相對誤差為4.22%，最小是廣東省，其平均相對誤差為0.93%；最后，根據預測的未來時期技術增長率測算未來時期最優的投入產出數據。

4.4 目標設置說明

本實證分析主要為了說明本研究的DEA模型的實際運用，因此，本實證的目標設定僅作為一個特例，具體設置說明如下(具體參數設置見表4)。

表4 實證中的各硬性目標的說明

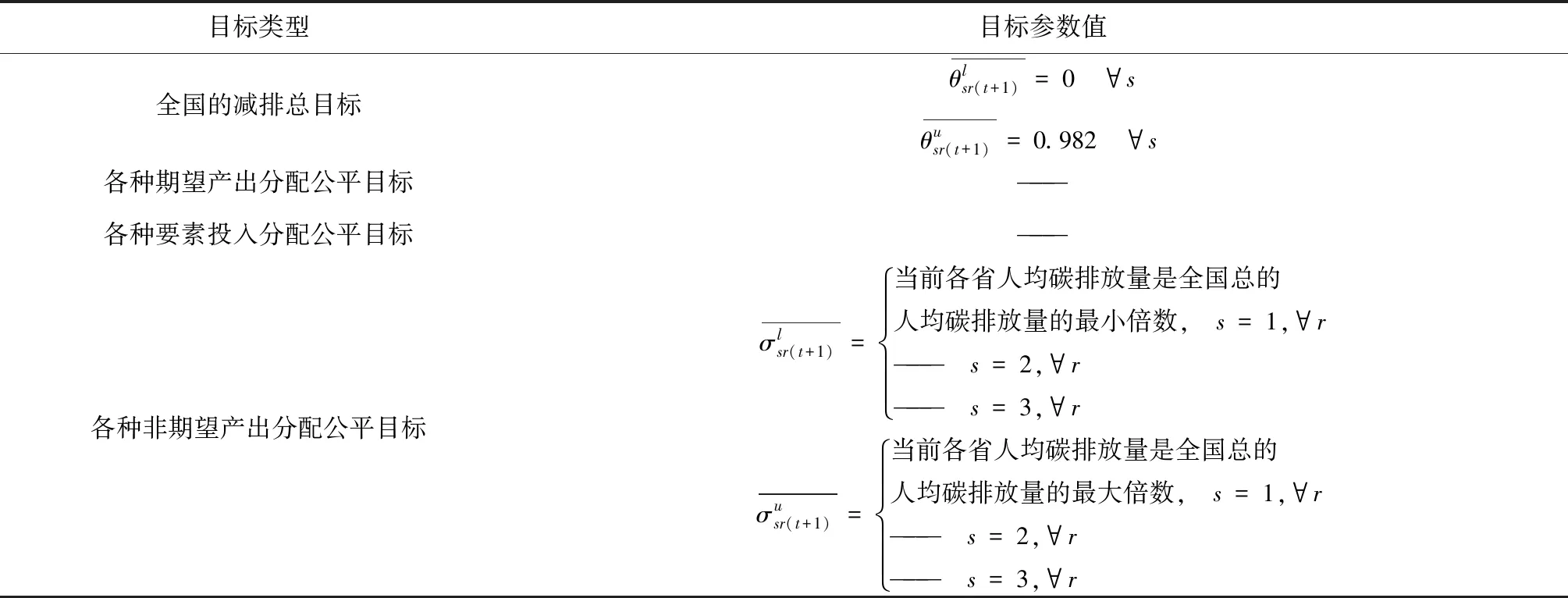
續表4 實證中的各硬性目標的說明

各省產出目標：未來時期各省區GDP不減少。

各省減排目標: 《中華人民共和國國民經濟和社會發展第十二個五年規劃綱要》明確要實現“化學需氧量、二氧化硫排放分別減少8%”，為了兼顧增長，因此將三廢的最大削減幅度設置為目標的2倍，即最大削減幅度為16%；三廢增長的上限設置為“十二五”期間全國三廢的年均增長額，從而保證各省三廢增長速度不超過“十二五”期間的年均增長速度。

各省節能目標：《中共中央關于國民經濟和社會發展第十三個五年規劃的建議》提出“能源資源開發利用效率大幅提高”， “十二五”期間全國能源投入年均增加5.65%，為了保證能源投入效率超過十二五水平，因此，將各省能源投入的增長上限設置為5.65%。和三廢的設置理由類似，為了兼顧增長，能源投入減少不超過16%。“十二五”期間全國資本投入年均增加16.23%，“十三五”期間固定資本投資增長率將很難超過“十二五”，因此，將各省資本投入的增長上限設置為16.23%。

全國的產出總目標：《中共中央關于國民經濟和社會發展第十三個五年規劃的建議》提出全國的GDP增長速度至少6.5%。

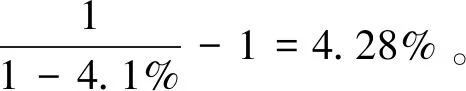
全國的減排總目標：《中華人民共和國國民經濟和社會發展第十二個五年規劃綱要》明確要實現“化學需氧量、二氧化硫排放分別減少8%因此，平均每年需要削減1.8%。

公平目標：未來時(第t+1期)期內，各省區人均碳排放量與全國總的人均碳排放量的最大偏離控制在現有范圍內；其他非期望產出的公平目標不設置。各種要素投入分配和各種期望產出分配的公平目標均不設置。

4.5 實證過程及結果

通過LINGO軟件實現DEA模型的效率評價和資源分配，具體的計算過程與結果分析如下:

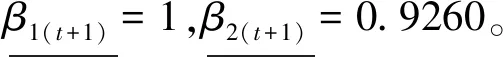
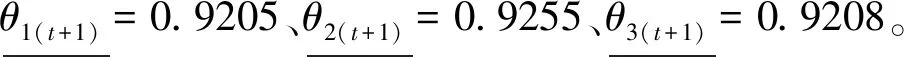
第三步，求解模型(4)，從而獲得實現管理者期望目標下的各省碳排放的分配結果(見表5)，將該分配結果與各省實際碳排放額相減，則獲得各省碳減排任務。

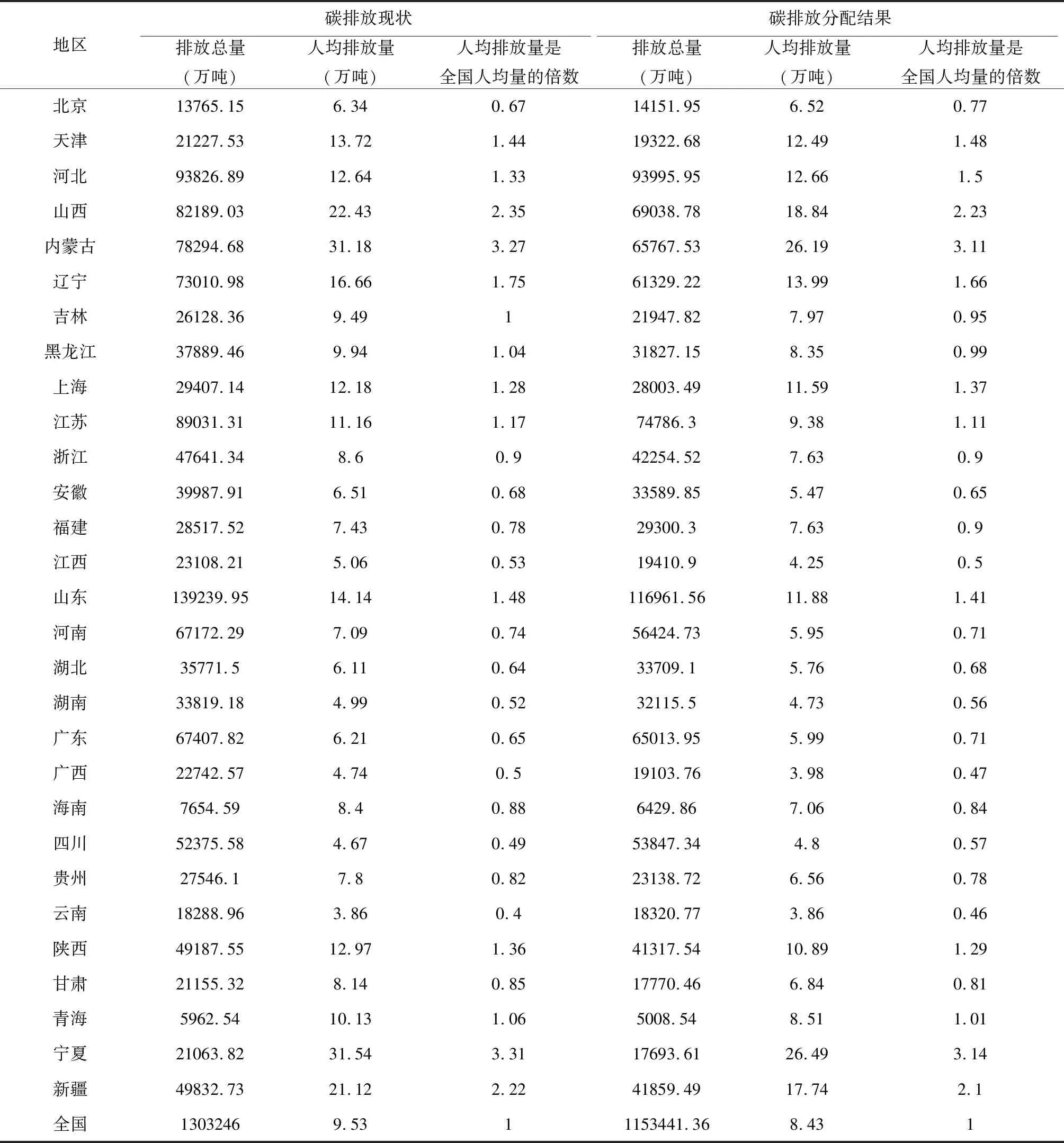
表5 各省碳排放現狀與分配結果的比較

根據表5的比較分析可以得知，本研究的分配方案中，全國碳排放總額為1153441.36萬噸，比當前碳排放總量縮減了8%，同時，各省人均排放分配量與全國人均量的倍數控制在(0.45，3.02)范圍內，比當前的(0.40，3.31)有所縮小，即，人均碳排放分配量與全國總的人均分配量的偏離有所縮小，更加公平了。

5 結語

本研究構建的基于未來效率的資源分配DEA模型具有以下的幾個特色：

首先，該DEA模型是基于未來效率對未來時期的資源進行分配。該模型根據以往的投入產出數據，預測未來時期的效率，從而實現未來時期的資源的最優分配。

其次，該DEA模型是在潛力評估的基礎上設定目標，從而使資源的分配方案更具可行性。該DEA模型分三階段在評估各DMU的要素投入的最大縮減潛力、非期望產出的最大縮減潛力期望產出的最大增長潛力的基礎上，根據管理需要選擇一個合理的目標。

第三，該DEA模型具有多目標決策的特點。管理者不僅可以改變九個硬性目標的參數值以及調整三個軟性目標的優先順序，而且還可以在每個步驟相應軟性目標最大實現潛力評估的基礎上，在相應目標的最大實現潛力范圍內進一步設定一個期望的合理軟性目標，從而形成各種目標導向的資源分配方案。這樣，更適合于管理者運用該分配模型進行分配方案設計。

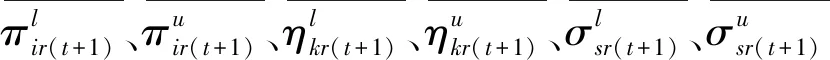
實證分析中，運用本研究構建的DEA方法靈活有效地解決了我國各省碳減排潛力評估及責任分配問題，一方面，在評估各省區經濟增長、節能、減排等方面潛力的基礎上，實現了全國碳排放總額比當前碳排放總量縮減了8%，另一方面，人均碳排放分配額與合理的人均分配量的偏離有所縮小，從而實現了兼顧公平與效率的碳排放額的分配。