初中數(shù)學(xué)解題策略的探究與應(yīng)用

☉江蘇省如皋市如皋高新技術(shù)產(chǎn)業(yè)開發(fā)區(qū)實(shí)驗(yàn)初中 陳衛(wèi)利

在數(shù)學(xué)解題中，思路和方法的選擇、應(yīng)用很重要.如果解題邏輯不正確，解題就費(fèi)時(shí)費(fèi)力，還難以獲得正確答案.在中考數(shù)學(xué)中，證明題型是重點(diǎn)，也是難點(diǎn)，對證明題型解題方法的學(xué)習(xí)，教師應(yīng)引領(lǐng)學(xué)生掌握基本解法，厘清解題思路，提高解題效率.

一、對初中數(shù)學(xué)解題策略的探討

拿到一道數(shù)學(xué)題，需要我們構(gòu)思解題思路.如求證某幾何題中兩個(gè)角相等，不同的學(xué)生面對求證目標(biāo)，其思考的方向也可能不同.總體而言，需要把握幾點(diǎn).一是正向求解.就是根據(jù)題中所給出的條件，從已知入手，一步步去推斷，最終得出求證結(jié)論.該思路是最常見的解題策略.二是逆向求解.就是不從已知入手，而是從結(jié)論入手，逆向推斷，直至可以利用已知條件進(jìn)行驗(yàn)證為止.該法主要應(yīng)用于已知條件偏少或者已知不明朗，從正向梳理解題思路未果時(shí)，可以嘗試逆向求解.不過，對于該法的使用，在求證時(shí)不能將結(jié)論直接當(dāng)成已知，但可以作為梳理解題思路的一部分，在真正解答時(shí)，還要以正向解題為主.三是正逆結(jié)合求解.對于正逆結(jié)合，可以先從正向解題，再融入逆向解題；也可以先從逆向解題，再融入正向解題.該法的應(yīng)用較少，多在已知與結(jié)論沒有直接關(guān)聯(lián)時(shí)才嘗試應(yīng)用.四是特殊題型的解法.針對特殊題型，在解法上也具有多樣性.如對于幾何類題、證明類題、應(yīng)用題型等，需要全面梳理題設(shè)，根據(jù)需要融入“畫圖”解法，嘗試引入作圖工具輔助解題.當(dāng)題設(shè)條件過多難以直接求解時(shí)，可以采用猜想逆推法，以不同的取值方式代入解題，進(jìn)而得出猜想，逆推解題過程，節(jié)省解題時(shí)間，找到更好的解題思路.

二、多角度拓展解題思維，提高解題準(zhǔn)確率

在初中數(shù)學(xué)中，解題思路的明確和選擇很重要.對于證明類題型，可以有多種證明方法，不同學(xué)生對題意的理解不同，得出的證明思路也不同.在平時(shí)教學(xué)中，教師要關(guān)注學(xué)生解題思維的激發(fā)，嘗試從多種視角梳理解題思路，幫助學(xué)生從多個(gè)角度形成證明過程，掌握多種解法.在面對題目時(shí)，能夠找到快速、高效的解題路徑，提升解題正確率.在證明兩個(gè)三角形中有兩條邊相等時(shí)，證明思路可以選擇“三角形全等”，接著尋找能夠證明兩個(gè)三角形相似的條件，逆向求證.如某題中，在圓O上作一條過直徑AB的端點(diǎn)A的切線AC，與直徑AB相等，連接OC與圓交于P點(diǎn)，CP的延長線與圓交于點(diǎn)F，求證CP=AE.如圖1所示.

從該題題設(shè)條件來看，求證某兩條線段相等的方法很多，我們結(jié)合題設(shè)與求證目標(biāo)，對比圖形來梳理解題思路.CP與AE兩條線段與哪些三角形有關(guān)呢？從圖示信息中，并不能找到兩者的直接聯(lián)系.在利用正向解題思維、逆向解題思維都無法找到求證的關(guān)鍵點(diǎn)時(shí)，我們可以結(jié)合兩種思維，從已知條件來進(jìn)行反思，要想獲得CP與AE相等的結(jié)論，還需要具備哪些條件？如果我們利用等量代換思想，可以從△CPE與△PCA入手，先求證這兩個(gè)三角形相似，當(dāng)△CPE與△PCA相似時(shí)，就可以得到PC∶PE=AC∶AP.同樣的道理，我們可以證明△APE與△APB也相似，進(jìn)而得出結(jié)論.

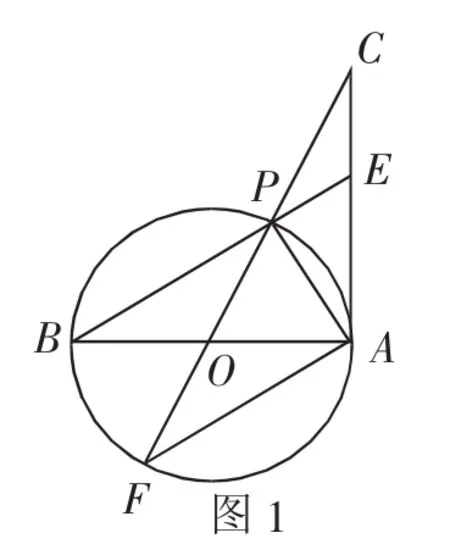
圖1

三、突出解題步驟的規(guī)范性，提高解題質(zhì)量

在數(shù)學(xué)解題過程中，解題方法與對應(yīng)的解題步驟具有邏輯性.平時(shí)，學(xué)生要注意解題方法的選擇，還要注重解題的規(guī)范性，特別是解題步驟要規(guī)范，避免出現(xiàn)解題錯誤.清晰的解題思路是前提，還要把握解題中關(guān)鍵點(diǎn)、關(guān)鍵信息的呈現(xiàn)，厘清解題需要哪些條件，如何將證明、求解過程準(zhǔn)確寫出來，讓教師能夠清晰了解解題過程.讓解題過程規(guī)范化，可以從具體題型解題中來實(shí)現(xiàn).如求證兩個(gè)三角形相似，對于三角形相似，需要具備哪些條件？如何證明兩個(gè)三角形相似？需要我們結(jié)合題設(shè)條件，遵循三角形相似要求來書寫證明過程.很多時(shí)候，學(xué)生習(xí)慣于從逆向視角尋找證明條件.但對于一些題型，題設(shè)與結(jié)論之間缺乏直接對應(yīng)性，或者說給出的條件較混亂，不能直接將求證過程寫出來.這時(shí)，我們就需要從現(xiàn)有題設(shè)條件入手，羅列與證明三角形相似有關(guān)的條件，繼而獲得求證過程.同樣，在證明兩個(gè)三角形全等時(shí)，我們?nèi)匀恍枰凑杖切稳鹊臈l件，找到相應(yīng)的條件，并按照求證三角形全等的步驟，將求證過程清晰羅列.所以，在解題時(shí)，學(xué)生要認(rèn)識到解題步驟的規(guī)范性，要保持卷面整潔，要對相關(guān)題設(shè)條件、證明過程進(jìn)行清晰、準(zhǔn)確呈現(xiàn)，為教師改評留下好印象，獲得高分.

四、培養(yǎng)推理習(xí)慣，增強(qiáng)解題邏輯思維

在解題時(shí)，推理思維是重要內(nèi)容.怎樣推理？首先，學(xué)生在面對題目時(shí)，要做好審題，仔細(xì)閱讀題設(shè)條件，聯(lián)系已有知識，對這些題設(shè)信息進(jìn)行發(fā)問，看有無解題突破口，與求證目標(biāo)之間還存在那些關(guān)鍵信息.其次，學(xué)生在解題時(shí)，注重對各題設(shè)條件的挖掘，從已知中推測中間量，借助中間量化解求證目標(biāo).再次，注重對推理習(xí)慣的培養(yǎng)，要能夠深入挖掘題設(shè)信息，掌握求證定理及運(yùn)用的方法，為解題奠定基礎(chǔ).如某題中，AC為圓的弦，AB為圓的直徑，過點(diǎn)C作切線CE，使得AD垂直于CE，垂足為D.求證AC是∠BAD的角平分線.如圖2所示.

對于該題的結(jié)論，求證角平分線，如果要滿足AC為∠BAD的角平分線，需要滿足∠BAC與∠CAD相等.在求證這兩個(gè)角相等時(shí)，結(jié)合題設(shè)，我們可以獲得哪些條件？從圖2來看，∠ACB為直角，O為圓心，OA與OB相等，AD垂直于CE.結(jié)合這些條件，我們可以得到∠ACD+∠CAD為90°；OC與OA相等，則∠OCA=∠OAC；OC垂直于ED，則∠OCA與∠CAD相等，進(jìn)而得出AC為∠BAD的角平分線.

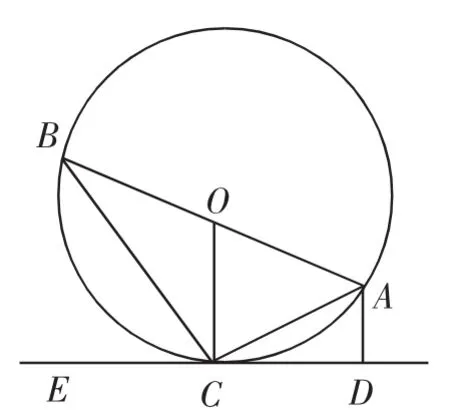
圖2

五、注重?cái)?shù)學(xué)思想的運(yùn)用，提升解題素養(yǎng)

在初中數(shù)學(xué)解題策略中，對數(shù)學(xué)思想的運(yùn)用很重要.常用的數(shù)學(xué)思想有分類思想、數(shù)形結(jié)合思想、函數(shù)與方程思想、化歸思想等.對于分類思想，主要是根據(jù)題設(shè)條件進(jìn)行分類概括.如對于三角形類題目，可以從三角形的特征、考查方向進(jìn)行概括，也可以從證明結(jié)論所需要的定理、思想進(jìn)行歸納.分類思想重在培養(yǎng)學(xué)生的分類意識，分情況來求解問題.數(shù)形結(jié)合思想是重要的解題策略，將抽象的數(shù)學(xué)問題與直觀的圖形相結(jié)合，便于學(xué)生優(yōu)化解題思維，抓住解題核心點(diǎn).在學(xué)習(xí)“反比例函數(shù)”時(shí)，某題題設(shè)條件有y=x-1、y=，當(dāng)y＞y1212時(shí)，求x的取值范圍.對于該題，如果將之轉(zhuǎn)換為x-1＞，求解不等式，則難度大.但如果我們分別參照對應(yīng)的函數(shù)圖像，發(fā)現(xiàn)兩圖像相交于（-1，-2）與（2，1）兩點(diǎn)，如此，我們只需要將兩個(gè)坐標(biāo)代入，從而得出x的取值范圍為-1＜x＜0或x＞2.函數(shù)與方程思想是中學(xué)數(shù)學(xué)的重點(diǎn)，該類題型主要涉及一些函數(shù)的性質(zhì)，如增減性、單調(diào)性、奇偶性、最值問題等.函數(shù)與方程思想，為我們求解問題提供了新的途徑.如某題中，要使方程x2-4x+k=0的兩根在1的兩側(cè)，則k的值是多少？根據(jù)題設(shè)，方程有兩根，則說明Δ＞0，再根據(jù)根與系數(shù)的關(guān)系，很快列出不等式組，從而求解k的值.同樣，我們還可以根據(jù)兩根分布于1的兩側(cè)，假設(shè)x=1時(shí)，該式的值小于0，則快速求解問題.另外，化歸法的應(yīng)用，主要是根據(jù)題設(shè)條件，通過化繁為簡、化難為易等方式，先求解次要問題，再求解目標(biāo)問題.

總之，解題策略的選擇和應(yīng)用，對于提高解題正確率意義重大.但是，面對不同的題型，需要學(xué)生認(rèn)真審題，挖掘和梳理題設(shè)條件，抓住突破口，拓展解題思維，找到解題思路，取得好成績.W