培養學生思維，踐行核心素養
——對一道中考壓軸題的思考

☉湖北省恩施州清江外國語學校 楊昌龍

核心素養的研究是當今的熱潮.研究中考試題對核心素養的評價，對教師在平時的教學中如何落實核心素養，具有很強的現實意義.下面就一道中考壓軸題為例，談談踐行核心素養的一些思考.

一、原題呈現，簡約精彩

原題：矩形AOCD繞頂點A（0，5）按逆時針方向旋轉，當旋轉到如圖1所示的位置時，邊BE交邊CD于點M，且ME=2，CM=4.

（1）求AD的長.

（2）求陰影部分的面積和直線AM的解析式.

（3）求經過A、B、D三點的拋物線的解析式.

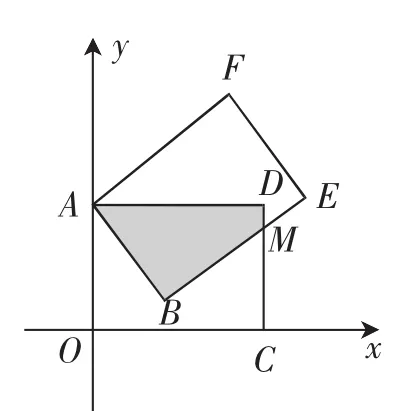
圖1

本題文字言簡意賅，圖形直觀、明了，從知識上看，考查四邊形、旋轉變換、勾股定理、方程模型等知識，融合了矩形、直角三角形及相似形、一元二次方程等有關知識；從核心素養方面看，考查學生直觀想象、數學抽象、數學建模、邏輯推理、數學運算等核心素養.下面從題目條件、圖形、設問等幾個方面進行分析.

1.條件設計精妙

題目條件寥寥數字，結合圖形，清晰明白.條件1：矩形AOCD在坐標系中，且兩邊在兩坐標軸上.條件2：點A的坐標為（0，5）.條件3：矩形ABEF是由矩形AOCD繞點A按逆時針方向旋轉而得的，且BE交CD于點M.條件4：ME=2，CM=4.

由條件1、2可知CD=OA=5，AD=OC. 由條件3可知AB=OA=5，BE=OC=AD. 由條件4可知ME=2，BM=BEME=AD-2，DM=CD-CM=OA-CM=5-4=1.

通過對題目條件的思考，發現題目條件在巧妙的構思中考查學生對矩形、圖形的旋轉等知識的掌握情況，更是對數形結合思想的考查，也體現了對直觀想象及邏輯推理等核心素養的考查.

2.圖形簡約、直觀

本題中的圖形由直角坐標系和兩個全等的矩形組成，簡約、直觀，且陰影部分清晰、明了.學生在分析圖形時，易看、易懂，容易接受，體現了對直觀想象核心素養的考查.

3.設問環環相扣

本題共四問，逐層深入，環環相扣.第（1）問求AD的長是后三問的基礎，因此第（1）問能否順利解答至關重要.第（2）問求陰影部分的面積和直線AM的解析式，只要第（1）問中求出了AD的長，陰影部分就可分解成兩個直角三角形進而求出面積.易知點M的坐標，也就可以求出直線AM的解析式.第（3）問主要是求B點的坐標，只要把B點的坐標求出來，就易求出拋物線的解析式.第（4）問是存在性問題，知道點A、M的坐標尋求P點，利用求三角形面積的方法不難得到方程組，但本問涉及分類思想和較繁的計算，給學生提供了一個較大的思維空間，學生不僅要具備較強的分析能力，而且要有較強的運算能力，因此學生要想得到滿分很困難.每一問相互聯系，逐次遞進，從不同角度考查了學生的數學建模、邏輯推理、數學運算等核心素養.

二、解法多樣，盡展風采

1.構建模型，層層遞進

本題第（1）問緊緊圍繞矩形的特征、旋轉的不變性，尋求等量關系，構建方程模型.本問對學生來說，有一定的難度，不易直接找到思考方法，特別是作輔助線利用相似三角形和勾股定理構建方程模型，或者直接利用勾股定理構建方程模型，是本問的難點.這一問不能突破，將直接影響后繼的解題，所以本問是關鍵.

圖2

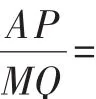
解法2：連接AM，設AD=x，由矩形的性質和旋轉的性質，可知AB=5，BM=x-2，DM=5-4=1.

在Rt△ABM與Rt△ADM中，52+（x-2）2=AM2=x2+12，進而可求得AD的長.

以上兩種解法，均是由勾股定理構建方程模型，解法1是由相似三角形及完全平方公式的變形獲得關系式，兩者的結合是本問的難點；解法2借助兩個直角三角形公共的斜邊構建方程.學生只要充分思考已知條件，想到方程，這樣層層遞進，逐級思考，就能最終獲得求解.

對于第（2）問，易得△ABP和△MBQ全等，通過勾股定理構建方程，求得MQ的長，于是可得BQ的長，陰影部分的面積就易得了，然后利用待定系數法求直線AM的解析式.也可直接求Rt△ABM與Rt△ADM的面積和.

對于第（3）問，只要確定B點的坐標，即可利用待定系數法求得拋物線的解析式.因此，求B點的坐標尤為關鍵.若第（1）問用三角形相似求解，則B點的坐標易知.若按解法2，則需要作輔助線求點B的坐標.

2.挖掘內涵，演繹分類

第（4）問屬存在性問題，是中考壓軸題常考的問題，全方位考查學生的能力，對學生要求較高.特別是分類思想，學生最易出現問題.因此，充分挖掘題目的內涵，找準關鍵所在，尋求恰當的方法，才能使問題得以解決.

方法1：設P點在線段AM下方的拋物線上時，過P點作縱軸的平行線，利用三角形面積為水平寬度與鉛直高度乘積的一半構建方程，從而求得點P的坐標.由P點的坐標，易求過點P且平行于AM的直線的解析式，從而得到P點到直線AM的豎直高度.通過平移，可得過線段AM上方拋物線上P點的直線的解析式，聯立拋物線和直線的解析式，進而求得P點的坐標.

方法2：求出了拋物線的解析式，掌握了求三角形面積的方法，自然可以得到各種情況，不需首先考慮分類.三角形面積是水平寬度與鉛直高度的積的一半.在拋物線上兩定點的水平距離稱為水平寬度，過動點作拋物線的對稱軸的平行線，與經過兩定點的直線相交，其交點和動點之間的線段的長度稱為鉛直高度.這樣第（4）問中，水平寬度為AD的長7，鉛直高度為動點P的縱坐標與交點的縱坐標差的絕對值，進而轉化成兩個一元二次方程，求出方程的解，即可得到動點P的坐標.

當然第（4）問在解一元二次方程時，計算較復雜，要求學生不僅有熟練的計算能力，而且要能靈活變形.

三、探究數學思想，貫徹核心素養

數學思想方法是解決數學問題的核心.中考壓軸題是滲透數學思想方法一個很好的平臺.本題從多個角度讓數學思想方法得到了充分體現，貫徹了數學學科核心素養的培養.

1.建模思想

新課程標準給出了數學學科核心素養的六個方面，其中一個就是數學建模.本題在第（1）問就是利用勾股定理構建方程模型，如解法（2）中利用Rt△ABM與Rt△ADM兩個直角三角形有公共的斜邊AM，作為等量關系，構建方程，從而求得AD的長.當然，本題中的模型構建有一定的難度，輔助線不易想到，入口較窄，致使學生思維受困.

2.數形結合思想

在壓軸題中，數形結合思想非常普遍，幾乎每道題都有涉及，通過坐標系建立起點與數的對應關系，既可應用代數方法研究幾何圖形的性質，又可借助幾何直觀，得到某些代數問題的解答.本題中數形結合較多，第（1）問求AD的長就利用點A的坐標得到了AB的長，進而獲得解答.第（3）問求拋物線的解析式，也是通過求點B的坐標，由待定系數法求得解析式.第（4）問更是體現得淋漓盡致，方法1就是通過圖形得到P點的幾種情況，把直線平移，得到其解析式，從而求得點P的坐標.無論是由坐標得線段長度，還是由圖形得到點P的坐標，都是從數到形，或者從形到數的過程，充分體現了數與形的結合.

3.分類討論思想

分類討論思想是對學生更高層次的考查，不僅檢測學生的知識水平，更檢測學生思維的準確性和嚴密性，常常通過條件的多變性或結論的不確定性來考查.本題的第（4）問就需要進行分類討論，點P在直線AM的下方，以及P點在直線AM的上方，求出P點的坐標后，還要進一步考查P點的合理性.

通過對本題涉及的思想方法的分析，中考題可以以不同的方式進行考查，但數學思想方法始終在壓軸題中得以體現，因此，平時的教學中，應強化對中考題的研究，注重數學思想方法的滲透，有效貫徹核心素養的培養.

四、引申推廣，拓展探究

1.改變條件

本題第（1）問還可以把條件改變，如：把邊BE交邊CD于點M改為直線BE交直線CD于點M，且ME=m，CM=n，這樣在求AD的長的過程中，就需要考慮M點的不同位置了，盡管結果一樣，但對學生的思維的要求提升了.還可把矩形旋轉改為矩形折疊，比如，恩施州2016年中考第24題.

2.改變結論

第（2）問求直線AM的解析式可改為求直線AE、AF、BF、EF等的解析式，主要考查學生對點的坐標及一次函數知識的掌握情況.

第（3）問求拋物線的解析式也可改為過點A、E、D的拋物線，過點A、F、D的拋物線等，主要考查利用待定系數法求二次函數的解析式.第（4）問是存在性問題，可改為求極值問題，比如，在直線AM下方的拋物線上找一點P，使三角形PAM的面積最大.

五、對教學的啟示

1.重視方法總結，探究渠道多樣

平時的教學中，教師應積極研究中考試題及命題方法，有意識地把相關的知識與方法貫穿于教學中.中考壓軸題的教學應注重以下幾個方面.（1）數學思想，主要是數形結合思想、分類討論思想、從特殊到一般的思想.大部分中考壓軸題幾乎都涉及這幾種數學思想方法的考查.本題就注重考查數形結合、分類討論及數學建模等.（2）探究問題，主要是三角形、平行四邊形（包括矩形、菱形、正方形等）、圓等的探究；動點、動線、動圖形的探究，比如，本題就是動圖形的探究；特殊角（直角、45°角、60°角等）的探究；線段極值、面積極值的探究；圖形變換中特殊點活動范圍的探究等.（3）解題方法，主要是直觀觀察法、數形結合法、解析法等.

2.注重學生能力，培養學生核心素養

數學學科核心素養的考查是每一份中考試題都必須關注的.壓軸題就是知識點的綜合，思想方法的集中，解決辦法的多變，思維高度的提升.從背景取材到問題設置，不僅綜合性強，而且創新性強，既注重知識的考查，又注重能力方法的考查，多方面考查學生的核心素養，從本題中可見一斑，方程的數學建模、畫圖后的直觀想象、變化圖形的數學抽象、每問的邏輯推理及最后一問運算能力的考查等都得以體現.因此，在平時的教學過程中，要重視知識的梳理歸納、計算能力的培養、實際問題中數學問題的抽象、數學思想方法的滲透等，最終達到培養學生數學學科核心素養的目的.W