光雷多站測元數據極大似然實時交會算法*

羅成強，胡秋平，張 華 ，胡文華

(1 陸軍工程大學石家莊校區，石家莊 050003；2 中國華陰兵器試驗中心，陜西華陰 714200)

0 引言

常規兵器外彈道測量，常采用多臺套光測(測元為A、E，A指方位角，E指俯仰角)、雷測(測元為R，指雷達距目標的距離)設備聯合組網/接力、中心引導的測量模式，完成武器系統外彈道測試。在這種模式下，中心引導需要實時完成武器系統的外彈道參數解算，并為組網/接力測量設備提供引導數據，數據解算要求解算精度達到米級，實時性要求處理時間≤50 ms。針對光、雷多站測元數據實時處理算法，目前還沒有統一的處理方式，一般根據具體任務采取相應的辦法(如R-AE交會處理，多站最小二乘算法(NLSE))[1]，上述算法一般受布站方式影響，存在較大的限制，如R-AE交會垂直角度盲區引起交會誤差急劇增加、最小二乘迭代不收斂引起死循環使得解算時間長等，在數據故障的情況下需要人工挑選組網/接力測量設備或者切換其它計算方法，不能夠完全滿足武器裝備外彈道測試實時性和測量精度要求。

對此，文中從概率角度出發提出一種基于距離估計的光電經緯儀-雷達多站測量數據極大似然交會算法，采用基于立體網格的模型實時求解方法，通過限定待求目標的空間坐標范圍，使得目標以目標初值為中心，以3倍的交會精度為半徑的保精度立體網格內，通過遍歷法求出每個網格的似然函數值，似然函數值最大的網格點就是解算出的目標坐標，網格劃分越小，定位精度越高。該方法避免了求解時間過長和可能發生的迭代死循環，仿真結果表明，目標坐標解算精度與多站最小二乘估計方法相當，6站交會情況下解算時間優于15 ms。

1 基于距離估計的光-雷多站測元數據交會算法(NMLE)

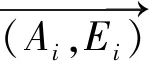
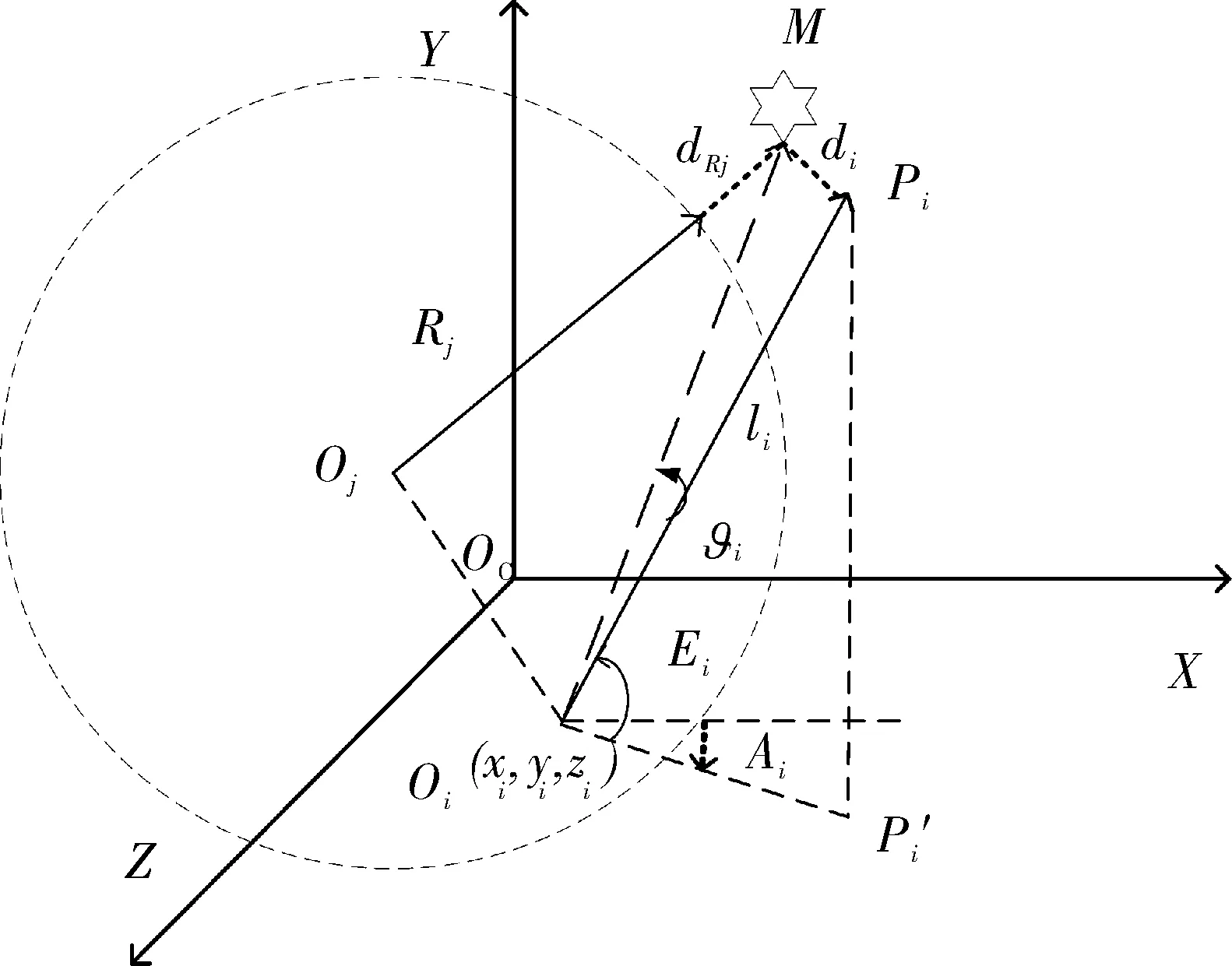
圖1 設備觀測示意圖

(1)

(2)

其中：

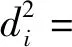
(x-xi)(z-zi)mihi+(y-yi)(z-zi)nihi),

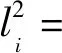
2((x-xi)(y-yi)mini+(x-xi)(z-zi)mihi+

(y-yi)(z-zi)nihi),

mi=cosAicosEi,ni=sinEi,hi=sinAicosEi。

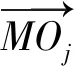
(3)

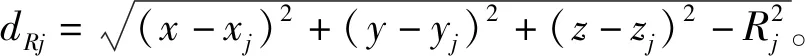
現有光測分站N臺，雷測分站M臺，則(N+M)臺觀測設備的多站似然函數為：

(4)

似然方程為：

(5)

根據極大似然原理，目標最有可能落在使似然方程極大的位置上，該位置即為目標的最優估計；即目標的最優估計模型為：

(6)

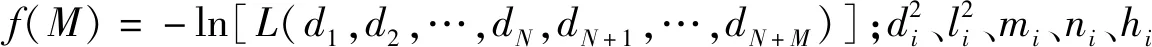
2 基于立體網格的模型實時求解

從式(6)可以看出，該模型為一無約束最優化求解問題，可以使用非線性無約束最優化解算方法進行解算迭代求解，要求初值(M0)要具有較好的精度值，使得迭代收斂較快，并且不易產生迭代死循環。理論上初值解算有兩種情況：一是兩站為光測站，則采用兩站極大似然算法求解M0；二是兩站為一臺光測、一臺雷達，則采用單站光雷算法(R-AE)[1]求解M0。但是從實時融合處理角度出發，為避免求解時間過長和可能發生的迭代死循環，采用通過限定待求目標的空間坐標范圍，使得目標按照初值大概率位于以初值為中心，以交會精度為半徑的保精度立體網格內，其中交會精度的給出根據初值求解算法精度按照實時系統的散布程度確定，這樣處理后就把式(6)轉化成有約束最優化問題，再通過遍歷法相結合求解，求出每個網格的似然函數值，似然函數值最大的網格點就是解算出的目標坐標。

2.1 保精度立體網格的確定

保精度立體網格的確定采用優選方法，方法是先從多站光雷中確定初值，該初值應該是所有采用兩站交會方法得出初值中精度最高的。初值確定后，根據相應的精度ε確定搜索網格半徑長度為3ε。當中心引導系統在某一時刻接收到各測量站的測元數據時，若第i站和第j站為不同的測站，則可依據參考文獻[1]計算其交會坐標M0和交會精度ε的值。

2.2 遍歷法求解

采用“遍歷法”求解式(6)，遍歷程序如下：

①接收多站測量數據，計算兩兩交會精度形成精度矩陣A。

②對精度矩陣A按照冒泡法排序得到精度最高測站精度ε。

③按照兩站交會得到初始點M0及立體網格半徑3ε。

④命k=0；定義遍歷步長H。

⑤計算f(Mk；令P=f(Mk)。

⑥若(k+1)H<3ε，否則Mk即為所求M(x，y，z)；計算f(Mk+H)，若f(Mk+H)<|P|，P=f(Mk+H)，進行⑦。

⑦命k=k+1，Mk+1=Mk+H；進行⑤。

3 算法分析

1)算法驗證

假定待求目標為M(x，y，z)，現有光測觀測設備N=2臺；現有雷測設備M=1臺，稱為測量分站O3，測元數據為R3。測元數據如下：

O1=(0，0，-1 000)，σ1=0.005，(A1，E1)=(90.005，45)；O2=(0，0，1 000)，σ2=0.005，(A2，E2)=(270.005，45)；O3=(0，0，0)，σR3=1，R3=999。

選取初始點(0，0，999)及網格步長0.2；最終求得M為M(-0.087 2，1 000，0)。從結果可以看出，求解值M(-0.087 2，0，1 000)與真值M(0，1 000，0)誤差小于0.1 m，計算結果是可信的。

2)仿真分析

為了評價算法是否滿足實時性和解算精度要求，設計以下仿真方案：仿真生成測元數據，包括理論彈道、分站站址坐標、分站測角精度、分站測元數據(加入觀測誤差)。針對某時刻數據，首先進行兩站(精度最高的兩站)交會計算估計坐標參數M0，并計算交會精度值，同時確定網格大小和遍歷步長；利用兩站交會初始值，進行多站最小二乘估計和極大似然估計，估計空間坐標參數，計算交會精度值；通過增加分站數量，改變布站方式，檢查有無無法求解的情況出現，最后統計NMLE算法的計算時間和處理精度。以某型火箭彈數據為例，理論彈道數據為幀頻20 Hz，時間25 s，距離0～15 km。

仿真結果如下：

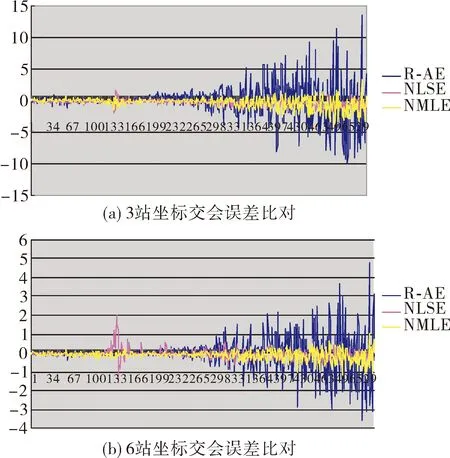
圖2 3種交會方法彈道坐標處理誤差比對

表1 NMLE極大似然算法數據處理結果表

從圖2 3種交會方法彈道坐標處理誤差比對可以看出，NMLE算法交會誤差精度相比兩站交會具有處理精度較高的優勢，與NSLE算法相當，6測站交會結果相對3測站也具有處理精度高的特點。從表1結果看出，6站交會情況下，NMLE算法交會精度在15 km范圍內優于3 m，處理時間優于15 ms。仿真結果表明，該算法實時處理時間、解算精度滿足要求。

4 結束語

文中提出一種基于距離估計的多站光雷數據極大似然交會算法，面向中心引導實時處理系統對處理時間和精度的需求，建立了基于立體網格的數值解算求解方法，算法不涉及迭代處理，沒有過基線、布站局限大、計算盲區等影響，通過對數值計算區域的限制(立體網格)解決了計算不收斂問題，滿足實時數據處理的要求。仿真結果表明，目標坐標解算精度與多站最小二乘估計方法相當，6站交會情況下解算時間優于15 ms，坐標解算精度優于3 m，目前該算法已經成功應用于某型外彈道測量數據實時融合處理系統中。