隨從力作用下薄膜的非線性自由振動特性研究

邵明月，武吉梅,，應戍狄，王 硯，盧 瑤

(1.西安理工大學 機械與精密儀器工程學院，陜西西安710048； 2.西安理工大學 印刷包裝與數字媒體學院， 陜西 西安 710048； 3.西安理工大學 土木建筑工程學院， 陜西 西安 710048)

作用于系統的非保守力隨結構的變形而變化，一般稱其為隨從力(follower force)或伴生力[1]，其作用機理與分布阻力有一定的相似性。非保守系統的動力學分析在工程中有著廣泛的應用，如運動的薄膜、飛行器等受到的空氣阻力都屬于非保守力。在印刷過程中，受到空氣阻力的影響，薄膜的振動會出現更為復雜的動態特性，從而嚴重影響印刷品的套印精度。本文以運動薄膜為研究對象，將空氣阻力模化為隨從力，對隨從力作用下的薄膜的非線性動力學特性及其穩定性進行研究，為印刷機的設計、制造以及印刷機的穩定性提供理論指導和依據。

對于隨從力作用下的系統運動穩定性研究，國內外學者已經做了大量的工作。Higuchi 和Dowell[2]研究了受到切向隨從力的柔性矩形板的動態穩定性，結果表明阻尼和板的長寬比對穩定性有很大影響。Choo 和Kim[3]采用多尺度法研究了四個自由邊受脈沖隨從力作用下的各向同性和非對稱層合板的動力穩定性。Alidoost 和Rezaeepazhand[4]研究了受集中隨從力作用下的分層組合梁的振動、屈曲和顫振不穩定性問題。Robinson 和Adali[5,6]應用微分求積法研究了切向均勻分布力和三角分布切向隨從力下粘彈性矩形板的動力穩定性問題。Lad 和 Kartik[7]研究了隨從力作用下軸向運動弦線的橫向振動特性，分析了隨從力和粘性耗散對系統特征結構的影響。Karimi-nobandegani等[8]應用有限元法研究了裂紋對分布隨從力作用下旋轉非均勻梁的顫振不穩定性的影響。李清祿等[9]研究了由陶瓷和金屬兩種材料組成的功能梯度材料(FGM)圓板在非保守隨從力作用下的穩定性問題。Wang等[10]應用無網格Galerkin方法研究了隨從力作用的粘彈性壓電層合板的穩定性。Guo等[11]采用微分求積法研究了均勻分布的切向隨從力作用下熱彈性耦合矩形板的動力特性和穩定性。

近年來，已有人對運動矩形紙帶非線性振動特性及穩定性進行研究。Marynowski[12]將運動薄膜簡化成梁模型，并采用Galerkin 法和4階龍格庫塔法研究了二維軸向運動薄膜的非線性振動特性。Soares 和Gon?alves[13]應用有限元法研究了拉伸超彈性薄膜的非線性振動和穩定性問題。Liu等[14]采用數值分析法研究了預應力矩形正交各向異性薄膜結構在沖擊載荷作用下的非線性振動響應。王硯等[15]采用微分求積法研究了非均勻張力作用下薄膜的張力變化系數、長寬比和運動速度對薄膜動力特性及穩定性的影響。Li等[16]研究了沖擊載荷下的各向異性薄膜結構的非線性振動響應，并進行了可靠性分析。

綜上，鮮見對隨從力作用下運動薄膜非線性振動的研究。本文以印刷運動薄膜為研究對象，研究隨從力作用下的薄膜的非線性振動特性。基于Von Karman薄板理論建立薄膜的橫向振動方程，應用Galerkin方法對振動偏微分方程組進行離散，利用數值法分析隨從力和無量綱速度對薄膜非線性振動特性的影響。

1 紙帶的非線性振動方程

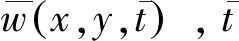
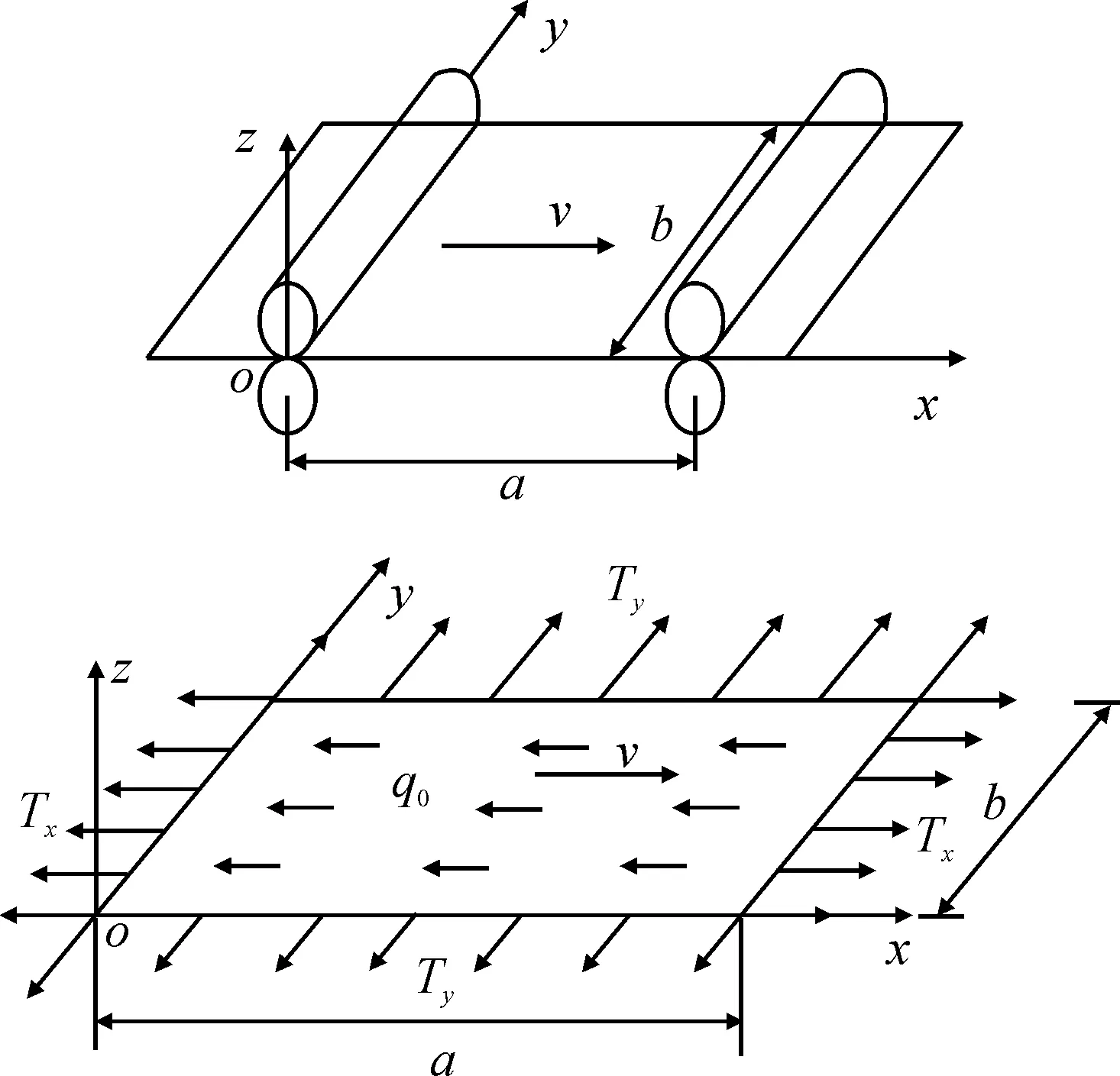
圖1 隨從力下運動紙帶力學模型Fig.1 The mechanical model for the axially moving web subjected to follower force

平衡微分方程為：

(1)

其中Nx、Ny、Nxy、Nyx是薄膜單位長度所受的張力值。

彈性曲面微分方程為：

(2)

式中，φ為內力函數。

由中面內力及撓度所表示的系統相容方程：

(3)

式中，μ為泊松比；E為彈性模量；h為薄膜厚度。

薄膜力用內力函數φ可表示成：

(4)

由于薄膜單元的各個平衡微分方程相互之間是獨立的，所以可認為：

(5)

根據Von Karman大撓度薄板理論[18]得到隨從力作用下運動薄膜的非線性振動方程組為：

(6)

對式(6)引入下列無量綱量：

(7)

則式(6)可化為無量綱形式：

(8)

對于上述大撓度振動的基本方程，其邊界條件為:

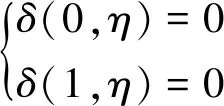
(9)

(10)

2 系統狀態方程

采用分離變量法和Galerkin法對式(8)進行離散，令:

w(ξ,η,t)=W(ξ,η)q(t)

(11)

f(ξ,η,t)=F(ξ,η)q2(t)

(12)

式中，q(t)為時間變量。

取滿足邊界條件的位移函數為：

W(ξ,η)=sinπξsinπη

(13)

將式(13)代入式(8)中，得到

(14)

求解式(14)，得出:

(15)

由Galerkin法得：

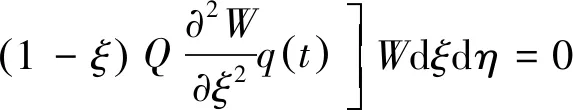
(16)

因此運動薄膜非線性振動的系統狀態方程為：

(17)

其中

(18)

則有:

(19)

其中:

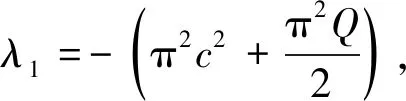
(20)

3 數值法求解

對式(19)首次積分得：

(21)

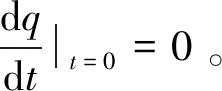
令:

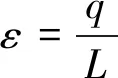
(22)

可以得:

(23)

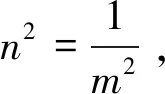
(24)

其中Z(n)為第一類完全橢圓積分，由此可得隨從力下運動薄膜非線性振動的頻率為：

(25)

其中:

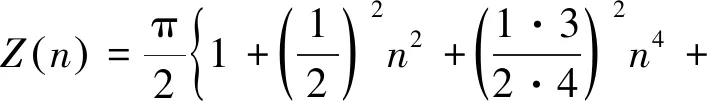
(26)

可得:

(27)

其中:

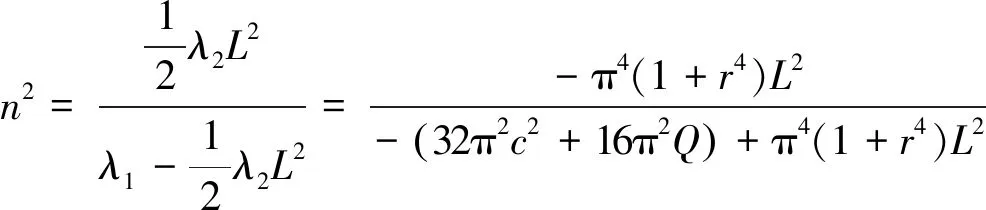
(28)

4 結果及分析

4.1 非線性振動頻率與隨從力的關系

圖2為初始運動條件L=1和無量綱速度c=0.5，長寬比r分別取0.5、1、2時，軸向運動薄膜非線性振動復頻率ω與隨從力Q之間的變化曲線。

令薄膜的長寬比r不變，由圖2可知：當隨從力Q=0時，無量綱復頻率ω是一個實數；隨著隨從力Q的逐漸增大，復頻率ω的實部逐漸減小，而虛部始終為零，說明運動薄膜進行的大撓度振動很小；當隨從力Q繼續增大到0.13，且長寬比r=0.5時，模態頻率ω的實部減小至零，當隨從力為0.195時，虛部開始由零逐漸增大，此時薄膜開始發散失穩。

因此，比較不同長寬比r的運動薄膜，可以明顯看出，長寬比r越小，隨從力Q越大時，薄膜越容易產生振動發散失穩現象。

圖3為初始運動條件L=0和無量綱速度c=0.5，長寬比r分別取0.5、1、2時，軸向運動薄膜非線性振動復頻率ω的實部和虛部與隨從力Q之間的變化曲線。

由圖3可知：隨著隨從力的逐漸增大，薄膜非線性振動的無量綱復頻率ω實部始終為零(即頻率ω為純虛數)，而虛部始終為定值。由此說明薄膜始終是發散失穩的，隨從力的變化不影響系統發散失穩的快慢，且該現象與薄膜的長寬比無關。

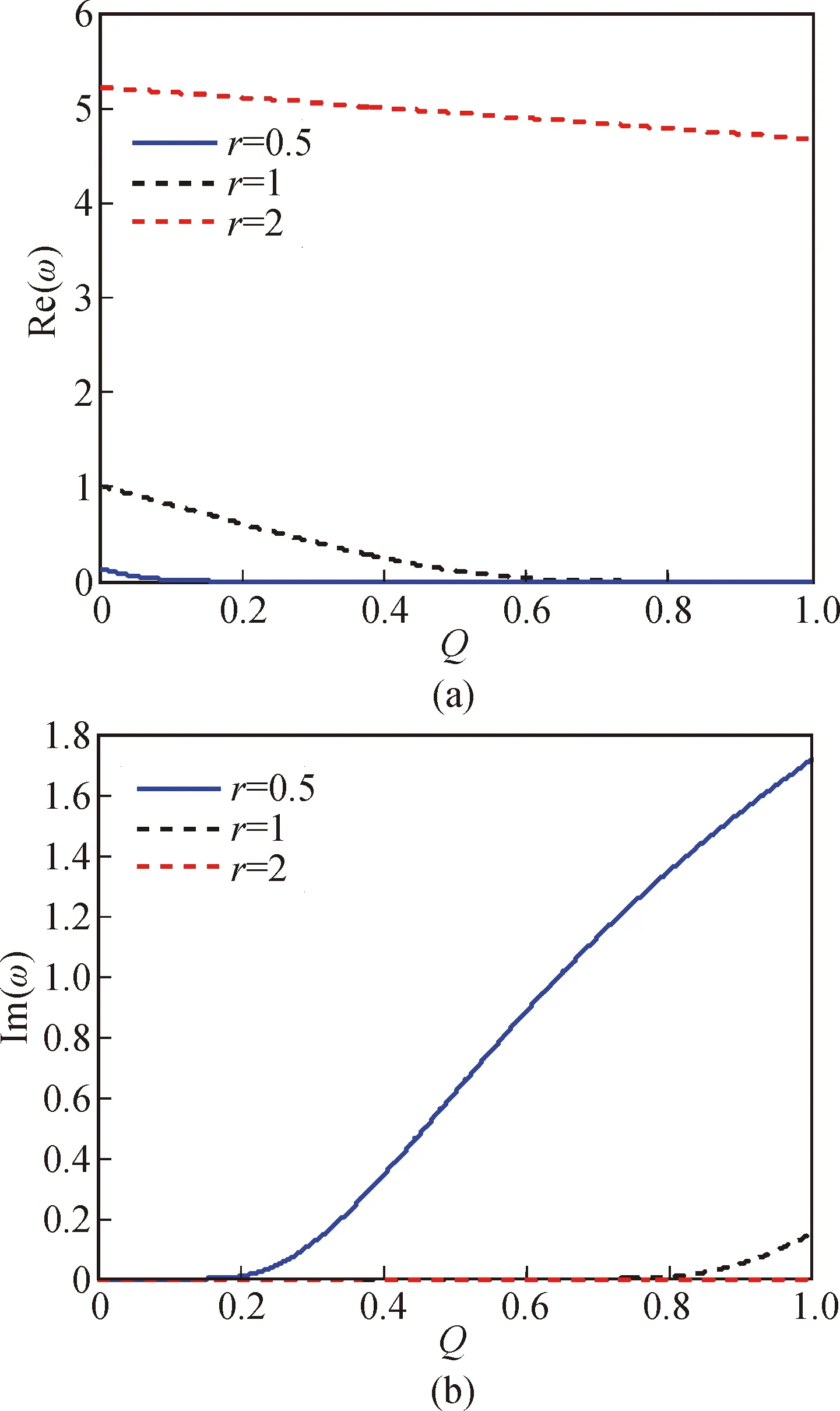
圖2 L=1時無量綱非線性振動復頻率ω與隨從力Q的變化曲線Fig.2 The relationship between dimensionless complex frequency and follower force when L=1

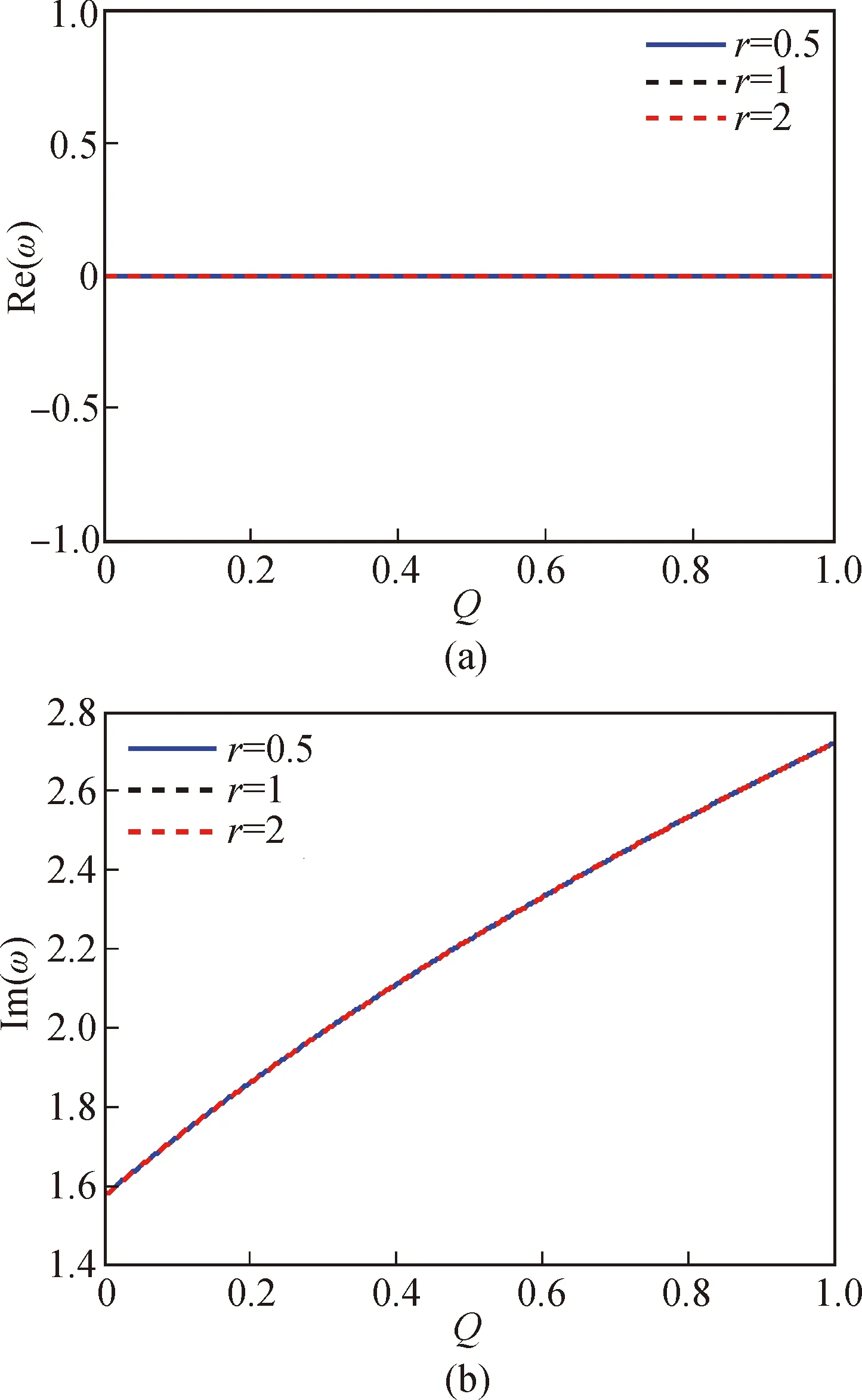
圖3 L=0時無量綱復頻率ω與隨從力Q的變化曲線Fig.3 The relationship between dimensionless complex frequency and follower force when L=0

4.2 非線性振動頻率與速度的關系

圖4為初始運動條件L=1和長寬比r=1，隨從力Q分別取0、0.5、1時，軸向運動薄膜非線性振動復頻率ω隨運動速度變化的關系曲線。

令薄膜的隨從力Q不變，由圖4可知：當無量綱速度c=0時，無量綱復頻率ω是一個實數；隨著無量綱速度c的逐漸增大，復頻率ω的實部逐漸減小，而虛部始終為零，說明運動薄膜進行的大撓度振動很小；若速度c繼續增大到某個值時，模態頻率ω的實部減小至零，而虛部開始由零逐漸增大，此時薄膜開始發散失穩。

因此，比較不同隨從力Q的運動薄膜，可以明顯看出，隨從力Q越小，薄膜振動失穩的臨界速度越大，也就是說，減小薄膜的隨從力Q可提高薄膜振動失穩的臨界速度，使失穩的臨界速度高于薄膜的工作速度，能夠有效地保證薄膜工作在穩定的狀態。

圖4 L=1時無量綱復頻率ω與無量綱速度c的變化曲線Fig.4 The relationship between dimensionless complex frequency and dimensionless velocity when L=1

圖5給出的是初始運動條件L=0，長寬比r=1，隨從力Q分別取0、0.5、1時，軸向運動薄膜非線性振動復頻率ω的實部和虛部隨運動速度變化的關系曲線。由圖5可知：隨著運動薄膜無量綱速度的逐漸增大，薄膜非線性振動的無量綱復頻率ω實部始終為零(即頻率ω為純虛數)，而虛部由零開始增大。由此說明薄膜始終處于發散失穩的狀態，速度越大，發散失穩越快，且該現象與薄膜的隨從力無關。

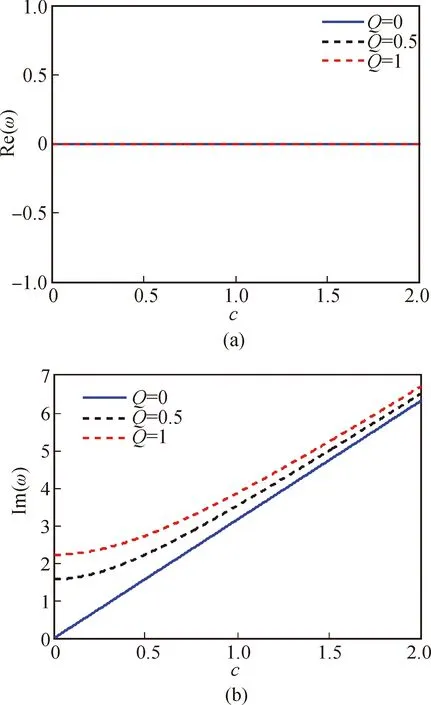
圖5 L=0時無量綱復頻率ω隨無量綱速度c的變化曲線Fig.5 The relationship between dimensionless complex frequency and the dimensionless velocity when L=0

5 結 論

1) 薄膜的非線性振動對初始運動條件有敏感依賴性，運動條件不同，薄膜的非線性振動特性有顯著差別。

2) 初始運動條件L=1和無量綱速度c=0.5，長寬比r越小，薄膜隨從力越大時，薄膜越容易產生振動發散失穩現象。適當增加薄膜的長寬比，減小隨從力，可有效避免大撓度非線性振動的產生。

3) 當初始運動條件L=0和無量綱速度c=0.5時，薄膜始終處于大撓度振動狀態，隨從力的變化不影響系統發散失穩的快慢，且該現象與薄膜的長寬比無關。

4) 初始運動條件L=1和長寬比r=1時，減小薄膜的隨從力Q可提高薄膜振動失穩的臨界速度，使失穩的臨界速度高于薄膜的工作速度，能夠有效地保證薄膜工作在穩定的狀態。

5) 初始運動條件為L=0，長寬比為r=1時，薄膜始終處于發散失穩的狀態，速度越大，發散失穩越快，減小薄膜無量綱運動速度c，可以有效避免大撓度非線性振動現象的產生。