基于能量損失率最小原理求解穩定滲流場的自由面曲線

王鳳梅，侯興民，鄭珊珊

(煙臺大學土木工程學院，山東煙臺264005)

0 引 言

壩體滲流自由面又被稱為壩體的生命線，只有計算出自由面的位置，才能得到準確的滲流域范圍。采用有限元法計算壩體穩定性，通常以壩體自由面為分割線。自由面以下視為飽和區，自由面以上為非飽和區[1]。用有限元法計算滲流場時，自由面的求解是關鍵。

在穩定滲流求解中，自由面應同時滿足水頭邊界條件和流量邊界條件，而自由面位置事先是未知的。國內外學者在解決該問題時，多根據水頭邊界條件或流量邊界條件逐步迭代逼近計算滲流自由面[2-5]，如自由面適應網格法[6]是同時逼近水頭和流量邊界條件的迭代計算；虛單元法[7- 8]、丟單元法[9]則是通過逼近水頭邊界條件的迭代計算；初流量法[10]、改進初流量法[11-13]、改進截止負壓法[14]是逼近流量邊界條件的迭代計算。采用以上方法計算滲流自由面時，為減少誤差，使計算結果更加接近實際的自由面，需提高迭代次數，從而增加了計算量。

本文提出了一種基于滲流場能量損失率最小原理確定穩定滲流場自由面的方法。首先對滲流場做有限單元劃分，計算滲流逸出點；然后由逸出邊界向上游邊界逐層推進有限單元，并基于能量損失率最小原理計算每層單元的自由面點，直至上游匯入邊界；最后將每一層的自由面點以及逸出點連線得到完整的自由面曲線。采用該方法計算了有電模擬試驗解的矩形壩、有甘油模型試驗解的矩形壩、有解析解的梯形壩，并與試驗結果或解析解作了對比，結果表明該方法具有很高的計算精度。

1 滲流域能量損失率最小原理

1.1 滲流域能量損失率

根據達西定律和地下水運動的連續性條件，不考慮土體和水體的壓縮性，均質各向異性土體的二維穩定滲流滿足以下控制微分方程：

??xkx?h?x+??zkz?h?z=0

(1)

式中，h為水頭函數；kx、kz分別為x方向、z方向的滲透系數。

對穩定滲流場，邊界條件有：①上、下游的水頭邊界條件；②自由滲出段的水頭邊界條件和流量邊界條件；③底部不透水邊界的流量邊界條件；④滲流自由面的水頭邊界條件和流量邊界條件。其中，②、④邊界是未知的。

根據給定的邊界條件，由式(1)求解滲流水頭函數等價于求滲流域Ω內泛函的極值問題[1]：

I(h)=?Ω12kx?h?x2+12kz?h?z2dxdz

(2)

式中，kx?h?x、kz?h?z分別為x、z方向的滲流速度；?h?x、?h?z分別為x、z方向的水力坡降，與滲透力成正比；γwkx?h?x2+kz?h?z2相當于單位時間滲透力做的功，數值上等于滲流域的能量損失率。因此，式(2)的積分I(h)與整個滲流域的能量損失率成正比。

對式(2)求極小值，將所得線性微分方程組匯總成如下的矩陣形式

[K]{h}={f}

(3)

式中，[K]為總滲透矩陣；{h}為節點水頭列陣；{f}為已知常數項列陣。式(3)為采用有限單元法計算滲流問題的基礎。

滲流計算域包括完全實域單元、自由面穿過單元、完全虛域單元3部分。本文利用侯興民等[18]對自由面穿過單元處理的方法，計算能量損失率時，考慮去除滲流計算域中的完全虛域單元與自由面穿過單元中的虛域部分所求的能量損失率最小值，與僅去除計算域中的完全虛域單元(后文將僅去除完全虛域單元后的計算域稱為滲流全域[18])所算得的能量損失率最小值，兩最小值對應的自由面點位置相同，故無需對自由面穿過單元作特殊處理。圖1為矩形壩滲流計算中的兩組坐標系：①以不透水層和矩形壩左邊界交點A為坐標原點，水平向右為x軸的正方向，垂直向上為z軸正方向的直角坐標系；②以下游水平面上任一點O為坐標原點，水平向右為正方向，垂直向上為正方向的直角坐標系。求解滲流自由面時，采用點A為原點的坐標系，設壩上游水位為h1，下游水位為h2，式(2)的泛函只考慮滲流全域，即由底部不透水邊界AF、上游匯入邊界AB、下游流出邊界EF、自由滲出邊界DE和滲流自由面BD所圍成的區域。計算滲流場的能量損失率時，采用點O為坐標原點的直角坐標系，其中，水平方向表示滲流逸出點(自由面點)位置不同時滲流全域能量損失率I(h)的大小，垂直方向表示滲流逸出點(自由面點)的坐標h。

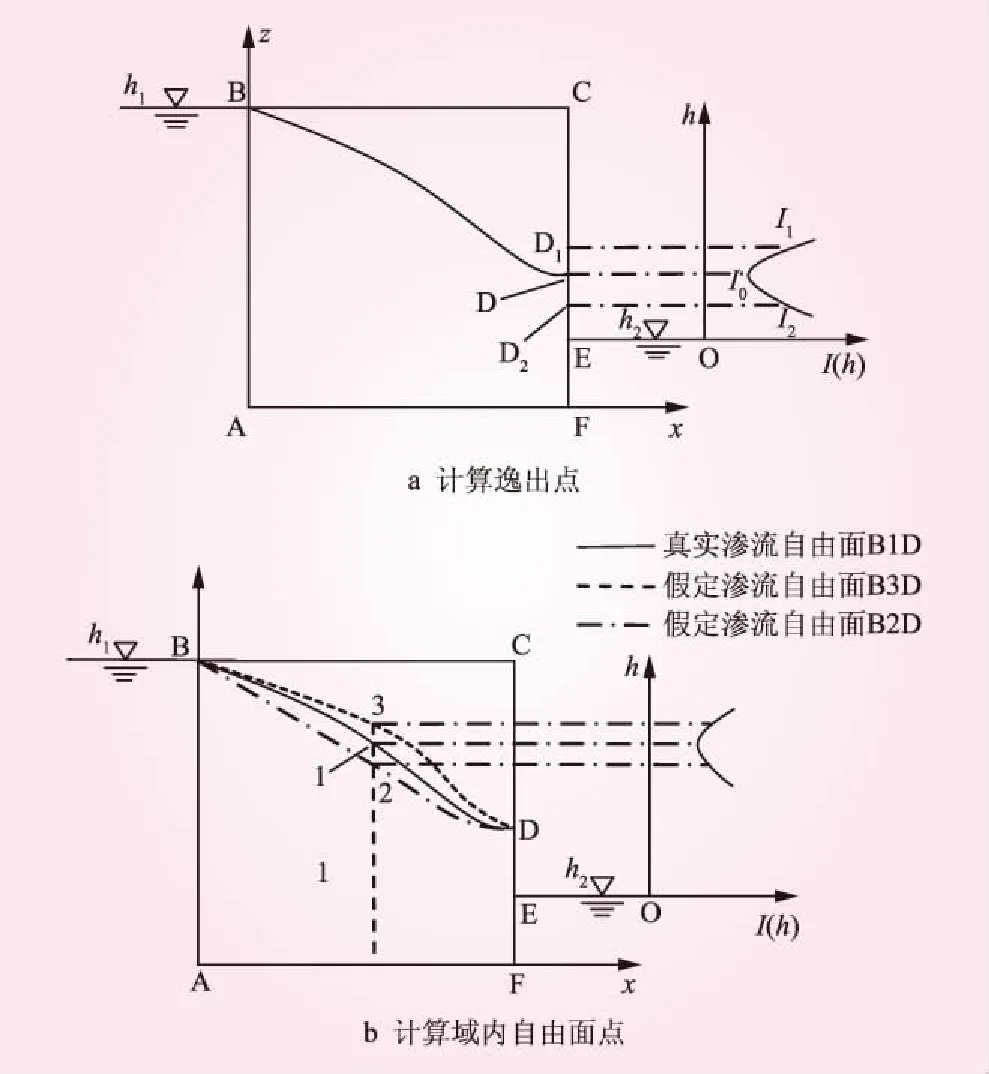
圖1 逸出點和自由面點的全域能量損失率變化示意

1.2 能量損失率最小原理

在已確定上、下游邊界的滲流場中，已知上下游以及逸出面的邊界條件，當滲流達到穩定狀態時，滲流全域的能量損失率最小，此時應滿足δI(h)=0[1]。

如圖1a所示，當滲流場達到穩定狀態時，設點D為真實的滲流逸出點，滲流全域內的能量損失率為I0；若其他條件不變，將滲流逸出點D抬高到D1點，滲流全域的能量損失率為I1，基于以上分析此時應有I1>I0。若其他條件不變，將滲流逸出點D壓低到D2點，計算出滲流全域的能量損失率為I2，此時也應有I2>I0。因此，在上、下游邊界確定的情況下，穩定滲流場中滲流逸出點總使得全域內能量損失率，也就是式(2)中的泛函I(h)最小。

同樣地，在已確定上下游邊界和逸出面邊界的條件下，當滲流達到穩定狀態時，圖1b中自由面曲線上的任一點都滿足使得全域能量損失率最小。設B1D為真實的滲流自由面，滲流全域B1DFA內的能量損失率為I1；若其他條件不變，將滲流自由面的1點抬高到3點，即自由面為B3D時，滲流全域B3DFA的能量損失率為I3，基于以上分析，此時應有I3>I1。若其他條件不變，將滲流自由面的1點壓低到2點，自由面為B2D時，計算出滲流全域B2DFA的能量損失率為I2，此時也應有I2>I1。因此，在上、下游及逸出邊界確定的情況下，穩定滲流場中使得滲流全域內能量損失率最小的位置即為所求的自由面點，這樣，求解自由面曲線，實質上成為求解I(h)最小值的問題。

2 基于滲流場能量損失率最小原理求解滲流自由面

圖3 有限元計算程序流程

2.1 基于能量損失率最小求解滲流自由面的原理

由能量損失率最小原理求解滲流逸出點位置，再由所求出的滲流逸出點向上游入滲點逐層單元逆推，每逆推一層單元，確定該層滲流自由面節點的位置，直至逆推到入滲點位置，將每層求得的自由面節點及逸出點連接成曲線即為所求的自由面曲線。以圖2所示的均質矩形壩為例，介紹基于能量損失率最小求解滲流自由面的原理。

首先，由能量損失率最小原理計算出滲流逸出點1，然后設點1左上方相鄰的節點2為此層單元的待求自由面節點，假定線段1-2為局部滲流自由面，賦予其自由面的邊界條件。不計其上虛域單元，計算全域的滲流能量損失率。依次調整假定自由面節點2的高程，按照1.2所述方法計算出滲流全域能量損失率最小所對應的節點位置，即為該層單元的自由面點。當自由面節點分別位于2、2a、2b位置時，域內能量損失率分別為I2、I2a、I2b。節點位于2處的全域能量損失率最小，所以2點即為該層單元處的自由面位置。依據上述原理，依次求解出各層單元滲流自由面節點的位置。將求解出的每層自由面節點、逸出點以及入滲點連成一條曲線，即為自由面。

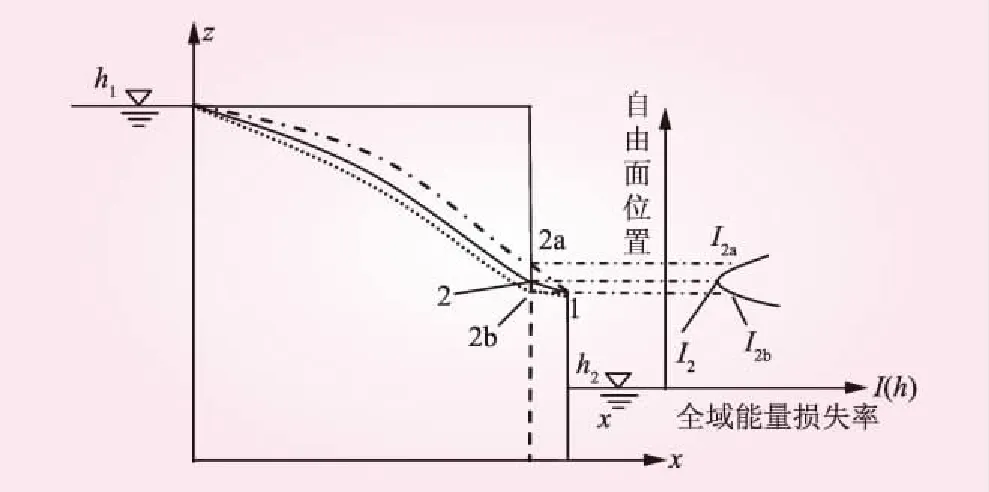
圖2 剖面2處自由面位置的計算

2.2 計算步驟

根據上述原理，采用Fortran語言編制求解平面穩定滲流場自由面的有限元程序，程序流程如圖3所示，具體計算步驟為:

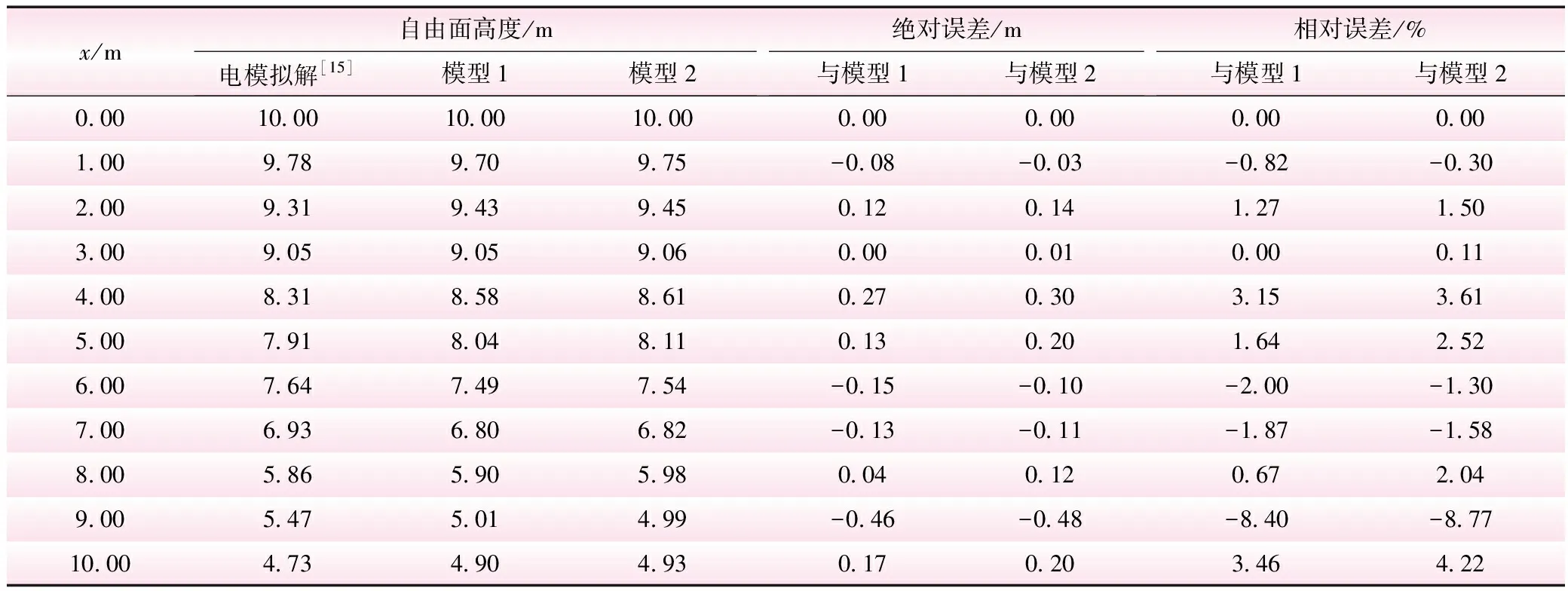
表1 有電模擬試驗解的矩形壩自由面計算結果比較

(1)選取六節點三角形單元劃分計算模型，假設在x軸方向共劃分了m層單元。

(2)假定逸出點初始水頭值為z0=h2+α。其中，h2為下游水位；α為最小誤差限(α的取值詳見本文算例1)。

(3)將已知的上下游和假定的逸出面各點水頭值代入式(3)中，求解計算域內所有節點的水頭值。引入單元分類函數pb(i)，若單元位于滲流虛區，即單元內三個角節點的水頭值與高程的差值均小于零，則pb(i)=0；反之，pb(i)=1。

(4)依據式(2)，計算滲流全域的能量損失率，即pb(i)=1單元的能量損失率總和。

(5)將假定的逸出點高程調整為z0=h2+nα，n為逸出點試算次數(n=1， 2， 3…)。重復步驟(3)～(5)，計算出相應的滲流全域能量損失In(h)。若In(h)In-1(h)，并依據圖1a計算滲流逸出點。

(6)由逸出點位置往上游方向逆推一層網格，如圖2所示，假定自由面節點位置為高于逸出點位置的節點2，連接1-2，不計其上的有限單元：可引入單元函數zb(i)以區分已求得的自由面(包括待求的前一層自由面)以上及以下的單元，zb(i)=0表示面上單元并丟棄；zb(i)=1表示面下的單元并保留。

(7)將已知的上、下游和所求逸出面各節點水頭值以及圖2中假定的待求自由面1-2的水頭值代入式(3)中，重復步驟(4)，求解計算域的全域能量損失率。

(8)將假定自由面節點高程調整為zq=zq-1+nα。其中，q為逆推單元層數；n為第q次逆推的試算次數。重復步驟(7)，計算出相應滲流全域的能量損失率In(h)。若In(h)In-1(h)；依據圖1b確定第q層的自由面點。

(9)由第(8)步確定的自由面節點往上游方向遞推一層網格，重復步驟(7)、(8)，直至確定出全部自由面點。將上游入滲點、逸出點以及確定的各自由面節點連成一條曲線，即為所求的滲流自由面曲線。

3 算例

3.1 計算模型1、2(與電模擬試驗解對比)

尺寸為10 m×10 m的均質土壩，上、下游水位分別為10 m和2 m，無垂向補給，其底部為不透水邊界，建立如圖4所示的2種有限元計算模型：①將矩形壩劃分為200個兩直角邊為1 m的六節點三角形單元，共有441個節點；②將矩形壩劃分為800個兩直角邊為0.5 m的六節點三角形單元，共1 681個節點。利用能量損失率最小原理分別求解兩種模型的自由面，與電模擬試驗解的精度進行對比，結果見表1。

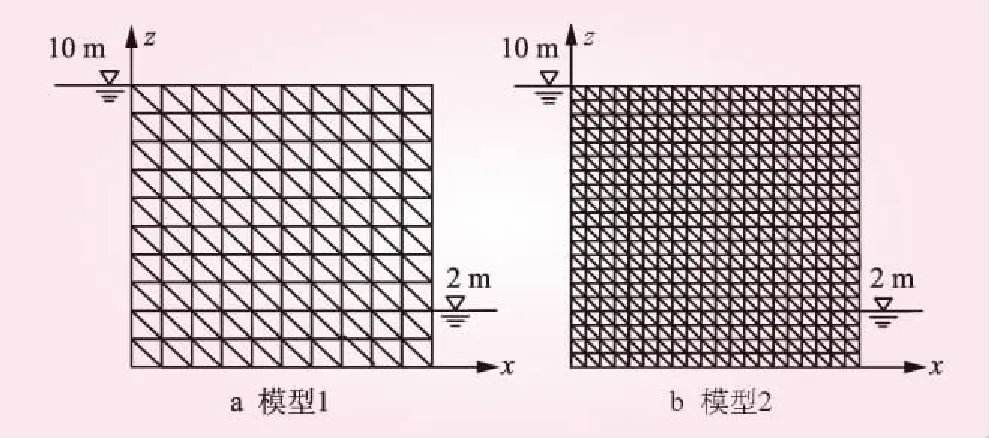
圖4 有限元計算模型

求解逸出點及自由面點時，α取0.01 m。由表1可看出，本文方法計算精度比傳統數值計算方法精度高。盡管也需要做多次調整自由面節點的位置以獲取能量損失率最小值，但是編制的有限元計算程序的計算速度快。不存在其他有限元法計算方法中可能出現的不收斂情況。

3.2 計算模型3(與甘油模型試驗解對比)

均質土壩尺寸6 m×4 m，上、下游水位分別為6 m和1 m，無垂向補給，其底部為不透水邊界。建立如圖5所示的計算模型3，將矩形壩劃分為48個兩直角邊長分別為1 m的六節點三角形單元，共有117個節點。本文方法與甘油模型試驗解計算結果的對比見圖6，精度對比見表2。

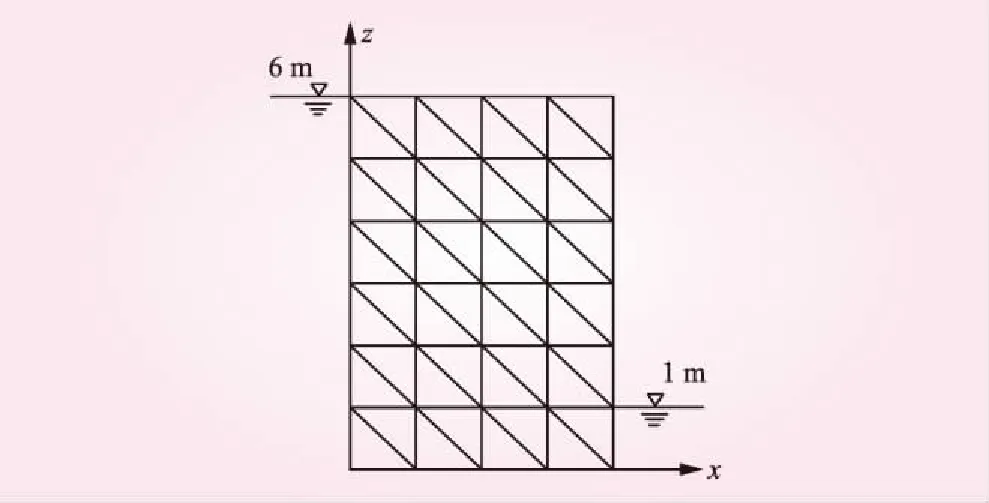
圖5 計算模型3網格劃分

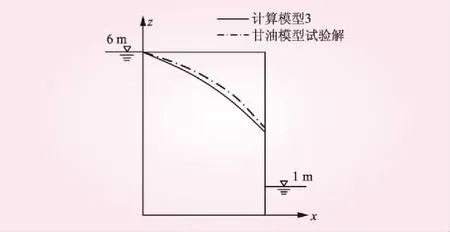
圖6 自由面位置比較

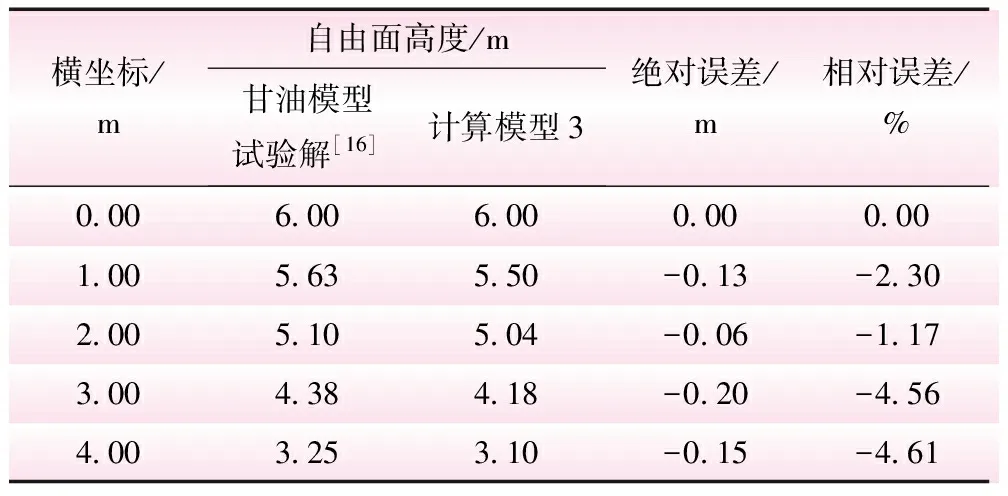
橫坐標/m自由面高度/m甘油模型試驗解[16]計算模型3絕對誤差/m相對誤差/%0.006.006.000.000.001.005.635.50-0.13-2.302.005.105.04-0.06-1.173.004.384.18-0.20-4.564.003.253.10-0.15-4.61

由表2可知，本文方法計算結果與甘油模型試驗解對比的最大絕對誤差為-0.20 m，最大相對誤差-4.61%，盡管單元劃分較少，該方法仍保持了很高的計算精度。

3.3 計算模型4(與解析解對比)

圖7所示為不透水地基上均質梯形土石壩，上游坡面邊坡系數m1=3，下游坡面邊坡系數m2=2。上游水位h1=15 m，下游水位h2=4 m。壩體高hHC=17 m，壩頂長lHG=12 m，壩底長lBE=97 m。壩體豎向三角形有限單元的劃分尺寸為1 m，其中BC、CD、DE段的橫向網格尺寸分別為3、2、2 m。基于能量損失率最小原理求解梯形壩上、下游水位之間的滲流自由面位置，與解析計算結果的對比見表3。

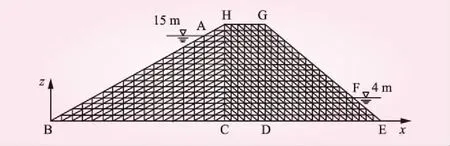
圖7 梯形壩的網格劃分

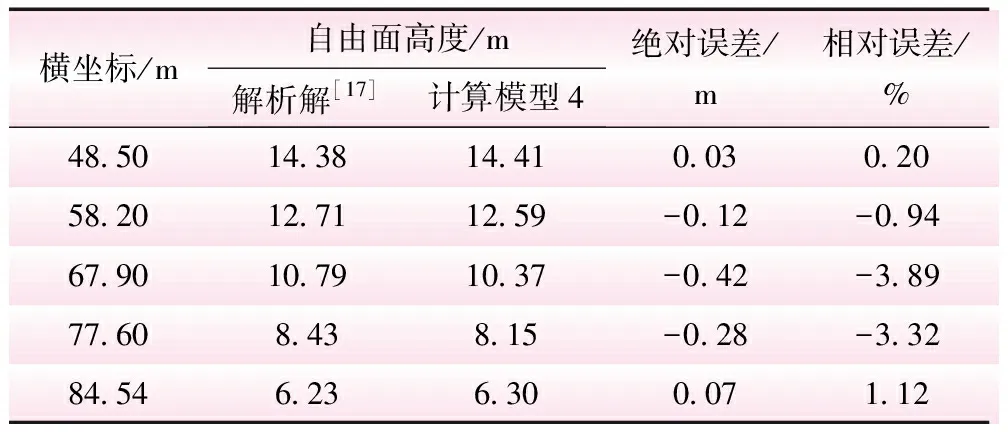
表3 有解析解的梯形壩自由面計算結果對比

由表3可知，本文方法計算結果與解析解對比，最大絕對誤差為-0.42 m，最大相對誤差為-3.89%，計算精度很高。

4 結 論

從泛函的物理意義出發，將穩定滲流場自由面的求解問題轉化為求解已知上、下游邊界條件和自由滲出邊界條件下，滿足滲流全域能量損失率最小條件的滲流自由面位置。依據全域能量損失率最小原理求出逸出點，基于該原理由逸出邊界逐層單元推至上游匯入邊界，將所求各層自由面點與逸出點連線得滲流自由面曲線。利用該方法求解了有電模擬試驗解的矩形壩、有甘油模型試驗解的矩形壩、有解析解的梯形壩的滲流自由面，并與試驗解或解析解作了對比分析，該方法具有很高的計算精度，計算結果穩定。

本文只驗證了二維穩定滲流場自由面的求解，應進一步論證所提方法在更復雜滲流問題中的適用性，所提出的逸出點求解及滲流自由面求解方法的理論研究以及工程驗證值得做進一步研究的課題。