基于共軛梯度法迭代優(yōu)化的圖像分類算法

楊子琳， 朱志斌， 馬金瑤

(桂林電子科技大學 數(shù)學與計算科學學院，廣西 桂林 541004)

近年來，基于深度學習的圖像分類受到越來越多人的關注，其典型模型是深度卷積網(wǎng)絡。深度卷積網(wǎng)絡主要由卷積層、池化層以及全連接層構成，通過一系列的卷積層與池化層將提取的圖像特征進行壓縮[11]，從而結合分類器，實現(xiàn)圖像的分類。

假設對于k分類，具有m個訓練樣本為{(x(1),y(1)),…,(x(m),y(m)),y(i)∈(1,2,…,k)}。深度卷積網(wǎng)絡最常用softmax作為分類器，該分類器是根據(jù)輸入x,估算出每個類別j的概率值P(y=j|x)。其中，softmax函數(shù)表達式為

(1)

其中：hθ(x(i))的每個元素P(y=j|x;θ)表示樣本x(i)屬于類別j的概率；θ為模型參數(shù)向量。

確定分類器的輸出后，圖像分類任務的目的是最小化模型代價函數(shù)：

(2)

其中，1condition表示condition為真時，其值為1，否則為0。因此，圖像分類的神經(jīng)網(wǎng)絡訓練問題轉化為通過優(yōu)化問題求解模型的最優(yōu)參數(shù)的問題。用于深度學習中的優(yōu)化算法主要有一階算法和二階近似算法。一階算法有固定學習率算法，如隨機梯度算法；自適應學習率算法，如AdaGrad算法[10]。二階近似算法如共軛梯度算法。

共軛梯度算法求解問題(2)的常用迭代公式為

xk+1=xk+αkdk；

(3)

(4)

其中：gk為目標函數(shù)梯度；dk為搜索方向；αk為步長，αk≥0；βk為迭代更新參數(shù)。通過改變參數(shù)βk，可得到不同的共軛梯度算法。著名的βk公式有FR、PRP、HS、DY等[4,7]。當目標函數(shù)保持嚴格凸性以及搜索時采用精確搜索，這幾個公式是一樣的，但當目標函數(shù)為一般函數(shù)時，它們存在顯著區(qū)別。對于全局收斂性，F(xiàn)R、DY公式表現(xiàn)良好[6,8]；數(shù)值效果上，HS、PRP公式占優(yōu)勢，但HS、PRP公式不一定收斂[1-3,9]。

1 一種修正的HS共軛梯度算法

受文獻[3，8]的啟發(fā)，通過改變參數(shù)θk、βk，提出了一種修正的HS共軛梯度算法：

(5)

(6)

其中，1≤μ≤2，yk-1=gk-gk-1。

對于任一線搜索，有

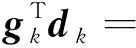
顯然，該算法的搜索方向均具有充分下降性。

算法步驟為：

1)初始化x0∈Rn,ε>0，ρ∈(0,0.5),σ∈(ρ,1),μ∈(1,2),k=1。

2)若‖gk‖≤ε，則停止；否則，轉步驟3)。

3)由Wolfe準則計算步長因子αk：

(7)

(8)

4)令xk+1=xk+αkdk。

5)令k=k+1，轉步驟2)。

2 全局收斂性分析

為確保問題(1)的局收斂性，作假設H：

1)f(x)在水平Ω={x∈Rn|f(x)≤f(x1)}有界；

2)f(x)在水平集Ω內連續(xù)可微，且滿足Lispchitz條件，則存在常數(shù)L>0，使得

‖g(x)-g(y)‖≤L‖x-y‖,?x,y∈Ω。

(9)

由假設H知，存在一個常數(shù)m>0，使得

‖g(x)‖≤m, ?x∈Ω。

(10)

引理1[2]若假設H成立，則算法是良定的。

由(7)可知，目標函數(shù)數(shù)值序列{f(xk)}是一下降序列，故有

結合式(10)得

(11)

在證明算法全局收斂性之前，首先給出新的搜索方向下Wolfe搜索下的Zoutendijk條件。

引理2[3]若f(x)滿足假設H，αk由式(7)、(8)確定，則有

(12)

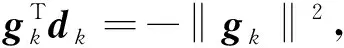
(13)

由式(9)得：

又由式(8)得：

所以，

(14)

結合式(7)、(8)得：

f(xk+αkdk)-f(xk)≤

兩邊同乘-1，并結合式(14)可得：

f(xk)-f(xk+αkdk)≥ραk‖gk‖2=

兩邊累加可得：

因f(x)在水平集Ω={x∈Rn|f(x)≤f(x1)}有界，故結論成立。

在此基礎上，進一步分析新算法的全局收斂性。

定理1若f(x)滿足假設H，xk由式(3)確定，αk由式(7)、(8)確定，dk由式(5)確定，則有

(15)

證明由式(5)中搜索方向dk的定義及式(9)、(10)、(14)可得：

‖dk‖≤‖gk‖+2μ‖gk-1‖2×

由式(11)可知，存在常數(shù)ρ∈(0,1)和正整數(shù)k，使得當k≥k0時，有

因此，對任意k>k0，有

‖dk‖≤m+ρ‖dk-1‖≤m+ρ(m+ρ‖dk-2‖)≤

m(1+ρ+…+ρk-k0-1)+ρk-k0‖dk0‖≤

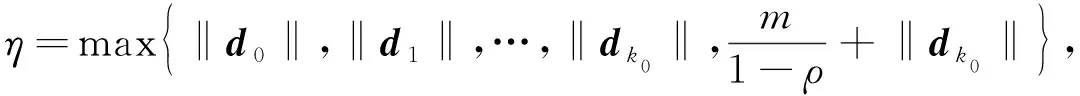
3 數(shù)值實驗

為了驗證本算法在圖像分類任務中能夠較快地得到模型的最優(yōu)參數(shù)，從而提升分類速度和分類準確率，對本算法進行數(shù)值實驗。其中，誤差ε=10-5，μ=1.8。

1)針對文獻[3]中的問題進行相關測試。本算法對不同維度的問題進行了相關測試，并與文獻[3]測試結果進行對比，結果如表1所示。

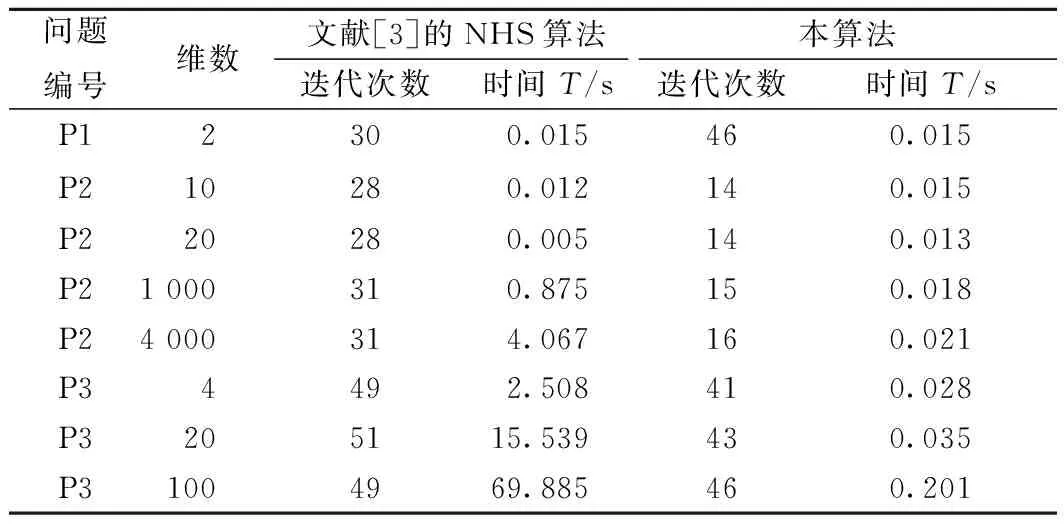
表1 本算法與文獻[3]算法的測試結果

2)將本算法應用于神經(jīng)網(wǎng)絡中。本實驗構造了一個簡單的二分類邏輯回歸網(wǎng)絡，用于識別貓。其中，訓練集為209張64×64×3的帶標簽圖片，測試集為50張64×64×3的帶標簽圖片，標簽為“1”表示貓，標簽為“0”表示不是貓。將本算法與神經(jīng)網(wǎng)絡中常用的隨機梯度算法進行對比，測試結果如表2所示，本算法在網(wǎng)絡中的成本損失如圖1所示。

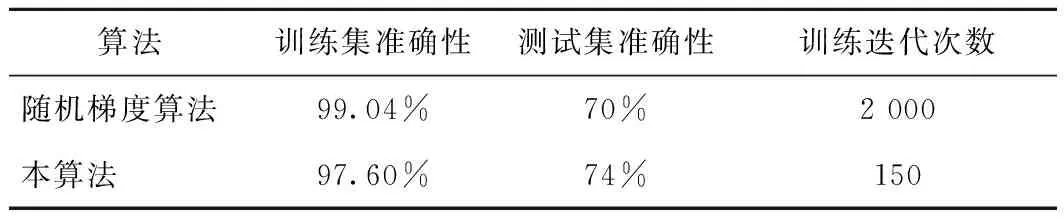
表2 本算法與隨機梯度算法的測試結果

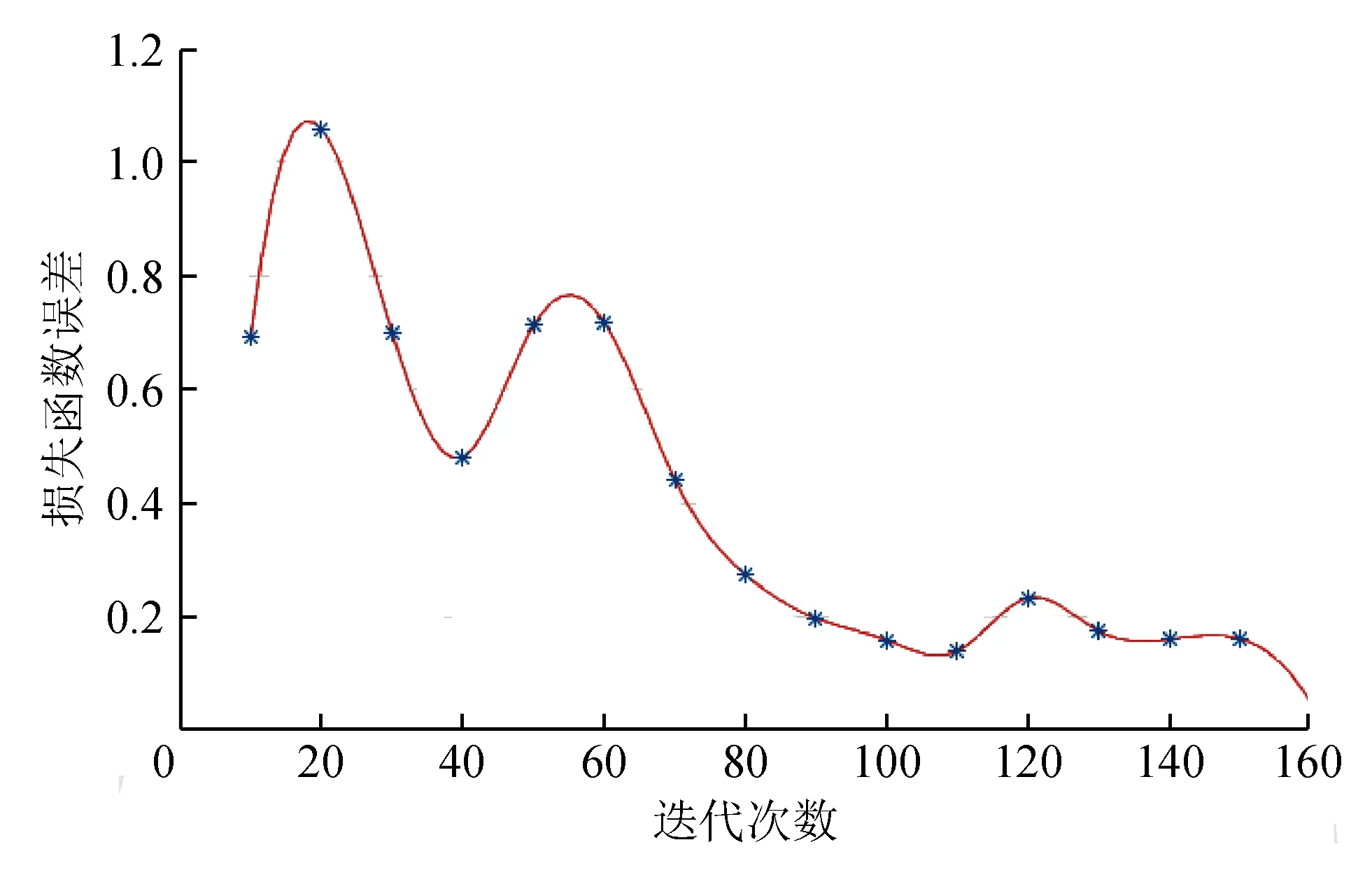
圖1 本算法在每10次迭代下的成本損失

從表1可看出，本算法在迭代次數(shù)較少及在維數(shù)較多情況下均能以較短的時間中求解到最優(yōu)解。從表2可看出，在邏輯回歸網(wǎng)絡中，本算法比隨機梯度法具有較少的迭代次數(shù)，測試集準確率有所提升。從圖1可看出，損失值隨迭代次數(shù)變化，最終趨向于一個較小的值。實驗結果進一步表明了算法的有效性。

4 結束語

基于傳統(tǒng)的HS方法，引入一個譜參數(shù)θk，通過對參數(shù)θk、βk的修改，提出了一種修正的HS共軛梯度算法。在Wolfe搜索下，證明了該算法具有全局收斂性，并通過實驗測試，進一步驗證了算法的有效性。