基于FTA方法的浮式風機基礎-塔柱系統定量風險分析

(天津大學 水利工程仿真與安全國家重點實驗室， 天津 300350)

0 引 言

海上風電場由復雜的大型風力發電機組成，需有高可靠性、可用性、可維護性和安全性。海上鹽霧濃度高、濕度大，有礙機械和電氣設備運行。風浪流的聯合作用也為風機運行帶來諸多潛在風險。海上風電大規模開發時間尚短、運行數據不足，不利于全面掌握其風險因素。已有研究表明，對于海上風電場，在一個項目的壽命中其操作和維護成本可占其電力成本的20%～30%[1]。采用合適的狀態監測(Condition Monitoring，CM)技術，可檢測許多故障，并在操作條件下對其進行控制[2]。海上風機發生的高概率事故主要出現在電氣系統、傳感器、葉片和變槳系統，損失嚴重的高停機事故主要發生在齒輪箱、主軸和軸承、塔柱、基礎和偏航系統[3]。

PéREZ等[4]通過對已有文獻數據的匯總和比較得出葉片和齒輪箱問題往往導致較長的停機時間，且大型風機比小型風機更易出現故障。BAI等[5]利用故障樹分析方法(Fault Tree Analysis，FTA)和失效模式與影響分析方法(Failure Mode and Effect Analysis，FMEA)相結合的分析方法對海上浮式風機吊裝和運輸風險問題進行分析和研究，并給出推薦的操作和管理措施。MARUGN等[6]采用臨界方法的FTA分析，考慮天氣因素，建立海上浮式風機各系統的故障樹，并給出相應的維修管理方法。JIN等[7]系統地歸納和總結現有風機故障評價方法，并對各方法的應用進行分析，為工程應用和研究發展做出指導。萬文濤[8]分析海上風機在運輸和安裝中的風險，研究表明考慮氣候、潮汐、浪涌、地質等因素的制約，海上風電的運輸安裝風險和安裝成本均高于陸地風電。郝二通等[9]研究基礎與船舶的碰撞風險，運用LS-DYNA 軟件數值模擬5 000 t船舶以2 m/s 的速度撞擊單樁基礎海上風機。

總體來看，目前對海上浮式風電系統的風險研究側重于風險識別過程，在分析中更多地采用定性分析方法，部分定量研究主要針對零件或單一風險事件展開。同時，FTA的底事件概率確定對SCADA工程數據和專家打分的依賴性較強。鑒于此，本文采用數值計算與概率統計相結合的方法確定海上浮式風機基礎-塔柱系統失效的概率，拓寬底事件概率數據來源，增強準確性，同時改進原有FTA方法，進行時域失效概率研究，并根據計算結果給出維修及風險控制建議。

1 基礎-塔柱系統風險識別與故障樹建立

引起基礎-塔柱系統最終失效的因素相對較多，關系也較復雜，本文最終采用FTA方法進行基礎塔柱系統的失效概率計算工作。FTA又稱事故樹方法，是安全系統工程中最重要的分析方法之一。FTA利用事件符號、邏輯門符號和轉移符號等描述系統中各事件之間的邏輯關系，從而達到系統可靠性分析的目的。

1.1 塔柱-基礎系統風險識別

基礎-塔柱系統整體上可分為兩部分，即基礎-塔柱部分和偏航系統部分，其主要故障類型可分為機械結構損傷和材料疲勞損傷兩方面。其中：浮式基礎結構易發生缺損、裂紋等表面結構損傷；環境腐蝕將貫穿于結構壽命的全過程；結構故障主要為疲勞破壞；偏航系統主要故障形式為齒輪磨損、斷裂和減速裝置過熱導致的效果不佳。基礎塔柱系統的主要失效原因為風載荷與波浪力產生的交變應力及其作用下結構的一系列響應，特別是在結構內部連接出現問題的情況下，容易出現異常振動，增加系統運行風險[10]；偏航系統故障的原因主要包括建造安裝和維護檢查兩方面，建造的精度不足會增加齒輪傳動的磨損，而在運行中的潤滑不佳又增強部件振動，縮短偏航系統整體壽命，影響風機系統運行[11]。

1.2 塔柱-基礎系統故障樹建立

在充分了解半潛型海上浮式風機故障類型與失效原因的基礎上，參考相關研究給出的FTA模型[12]，建立海上浮式風機基礎-塔柱系統的FTA模型，如圖1所示，并針對結構過載損傷和連接疲勞進行詳細的失效概率計算，結合OREDA數據庫和已有研究對其他風險事件做出概率估算。

圖1 基礎-塔柱系統故障樹模型

2 基礎-塔柱系統失效概率計算

考慮到海上浮式風機基礎-塔柱系統的風險類型和在分析方法上的區別，本文將塔柱基礎系統的風險事件分為結構風險事件和非結構風險事件。

2.1 結構風險事件失效概率計算

在結構風險計算上采用有限元數值分析方法。彌補目前浮式風機風險分析缺乏工程數據支撐的缺陷，增加故障樹底事件概率的來源，彌補通常依靠專家打分、數據庫和風險等級等方法選取概率的精確性問題，更為結構設計階段沒有實際作業數據的情況提供風險評估方法。

2.1.1 塔柱-基礎系統故障樹建立

適用于FTA分析的概率分析模型大致可分為3類，即隨機概率模型、時間相關概率模型和物理參數可靠性模型，而與結構相關的過載和疲勞分析通常采用物理參數可靠性模型進行概率模擬。其對數正態分布的可靠性表達式[13]為

(1)

式中：Ф表示正態分布；s為對數正態分布的形狀參數，在該研究中取值為0.1[14]；k為許用應力，本文采用S355鋼進行計算，安全因數取1.1，故k值為323 MPa；Xmax為最大應力。

國內外學者的分析研究給出動態可靠性模型計算公式為

Rt=exp[-(1-R)·α·t]

(2)

式中：Rt為結構的動態可靠度；R為式(1)靜載荷作用下結構的可靠性；α為該載荷的年循環次數；t為服役時間，a。

2.1.2 有限元模型建立

采用有限元分析方法，以OC4半潛型浮式風機為研究對象，根據具體參數建立浮式基礎三維模型，如圖2和圖3所示，具體有限元參數如表1所示。

圖2 浮式基礎三維視圖(SESAM模型) 圖3 浮式基礎三維視圖(ANSYS模型)

表1 有限元分析相關參數

2.1.3 相關載荷與邊界條件計算

考慮浮式風機的工作特點，分別對額定工況、切出風速工況和極限工況下的3種波浪環境進行模擬，具體工況參數如表2所示。

表2 環境載荷計算參數表

根據《CCS海上移動平臺入級規范(2012)》的風載荷及風傾力矩計算方法，分別計算在不同工況下的風載荷與風傾力矩情況，將極限風速下的結果匯總于表3。

表3 極端工況風壓載荷計算表

在風載荷計算中，將錐筒型塔柱劃分為8段進行計算，同時對中心立柱和浮筒水面以上部分風載荷進行計算。表中具體參數如下：D為構件直徑(前者為上直徑，后者為下直徑)，H為構件頂端高度(基于水平面)，S為構件迎風面正投影面積，Cs為受風構件形狀因數，Ch為受風構件高度因數，V為H高度處的平均風速，F為構件風壓載荷，M為構件風傾力矩。

根據表2，采用譜峰因子為1的3個JONSWAP譜產生隨機波，其波幅時域曲線如圖4所示。根據結構動力學相關知識，一階波浪力可表達為波浪幅值與波浪力傳遞函數乘積的形式：

圖4 波浪幅值時域曲線

式中：A為入射波波幅；ω為入射波角頻率；β為入射波傳播方向；φ為入射波的初始相位；t為時間；H(ω,β)為波幅-波浪力計算傳遞函數。通過SESAM HydroD計算半潛型浮式風機在0°浪向角下一階波浪力傳遞函數，最終計算得到一階波浪力時域曲線如圖5所示。

圖5 一階波浪力時域曲線

計算作業海域出現的最大流速，考慮流速垂向分布，在極端海況下的流壓計算如表4所示。

表4 極端海況下不同水深處的流壓計算

位移邊界：考慮浮式風機基礎運動，在ANSYS瞬態分析中，將結構升沉和縱搖運動以動邊界的方式施加到浮式基礎上，盡可能真實還原結構的運動和受力狀態，采用FAST計算其升沉和縱搖運動的時域結果，如圖6和圖7所示。

圖6 升沉運動時域曲線 圖7 縱搖運動時域曲線

2.1.4 結構失效概率計算

采用S355高強度鋼作為材料進行分析，其屈服應力為355 MPa，彈性模量為208 GPa，泊松比為0.3，考慮工程實際，取安全因數為1.1，則許用應力為323 MPa。采用ANSYS瞬態分析，考慮塔柱與基礎連接處作為危險節點，在3種工況載荷作用下，其應力變化如圖8所示。圖8表明，在定常風壓作用下，塔柱的應力大小逐漸趨于穩定，最大應力出現在開始階段。對基礎過載事件，考慮主斜撐與浮筒連接處存在應力集中現象，以主斜撐-浮筒連接點作為危險節點，在3種工況下應力變化的時程曲線如圖9所示。

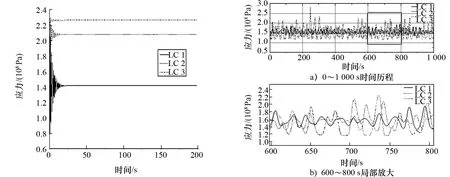
圖8 塔柱基礎連接點應力曲線 圖9 基礎-主斜撐連接點應力曲線

在疲勞分析中，采用Dirlik表達式作為危險節點應力時間歷程雨流計數過程的概率密度函數，其表達式[14] 為

(4)

考慮疲勞極限服從正態分布，其概率密度函數可表示為

(5)

式中：μ為疲勞極限均值；σ為疲勞極限方差；xn為節點強度的統計值；V=σ/μ。結構的失效概率可表示為

(6)

采用雨流計數法，對3種工況下的主斜撐-浮筒連接點應力值進行統計，確定不同工況下的平均應力、應力幅值和各應力幅值的出現次數，對不同應力幅值的出現進行概率密度統計。圖10和圖11以在切出風速工況下的計算結果為例，給出主斜撐-浮筒連接點的平均應力與峰值應力統計圖和循環應力概率密度曲線。

圖10 LC 2下平均應力與應力峰值次數統計 圖11 LC 2下循環應力幅值概率密度

采用應力結果統計方法，同時考慮選用材料的疲勞應力參數，將其代入式(6)進行疲勞時效概率計算，可得結構風險相關事件的失效概率，具體結果如表5所示。

2.2 非結構風險事件的失效概率計算

由于環境腐蝕事件貫穿結構壽命的全過程，且海洋結構物通常具備較好的防腐措施，而焊縫損傷會受人為因素影響，可認為二者的失效概率為最低等級，即0.000 1。極端風載荷可采用威布爾分布進行模擬[15]，在結構物自存狀態的極限風速為51.5 m/s的情況下，可計算事件的發生概率約為0.002 6，則其年平均失效概率為0.001 39。關于螺栓的斷裂和松動，其年失效概率應為0.001 53。對于偏航系統的機械故障，通過已有文獻[16]的查閱，可知其年失效概率約為0.013。

表5 基礎塔柱系統基本事件的失效概率匯總表

續表5 基礎塔柱系統基本事件的失效概率匯總表

3 全生命周期FTA定量計算

采用MATLAB語言編寫時域動態故障樹程序，基本邏輯運算基于傳統的FTA方法完成，考慮部分風險事件的失效概率隨服役年限的增長會明顯升高，采用不同概率統計模型實現對失效概率的時域動態描述，其中物理方法的動態可靠性模型如式(2)所示，而隨機指數型與隨機常數型的可靠性模型如式(7)和式(8)所示：

Rt=e-λ·t

(7)

Rt=1-t·(λ/t)

(8)

式中：λ為事件的靜態失效概率；t為服役時間。

圖12 失效概率對比

根據文獻[17]提出的記憶強度還原模型算法，對定期維修進行初步研究，計算模型為

λt=(1-ρ)·λT

(9)

圖13 底事件概率重要度因數變化曲線

式中：λt為修復后系統的恢復失效概率；ρ為不完全維修因數(越大則維修程度越高)；λT為維修前系統整體失效概率。本文計算采用該模型。

3.1 有/無維修情況頂事件發生概率對比

將前文計算得到的失效概率輸入編寫好的FTA時域分析程序，在考慮每5年維修一次、不完全維修因數為0.5的情況下，得到有、無維修狀態下的失效概率曲線如圖12所示。

由圖12可知，水平軸浮式風機塔柱-基礎系統在無維修的情況下，當達到服役年限時失效概率約為0.000 7，而在維修周期為5年的情況下，其最終失效概率下降約60%，僅為0.000 3，在很大程度上延長了塔柱-基礎系統的使用壽命，提高結構使用的安全性。

3.2 基礎-塔柱系統底事件概率重要度分析

考慮服役年限為25 a，通過時域動態FTA程序計算，可獲得各底事件的概率重要度因數隨服役年限的變化規律，如圖13所示。

圖13表明：在服役年限內塔柱基礎系統整體上保持較低的失效率；事件7(極端環境載荷)在整個壽命周期內的重要度最突出，隨服役年限增長，極端環境載荷對結構的危害性逐年增加；事件1～事件6隨服役時間的增長，重要度逐年增加。這證明本文提供的關于結構的安全評價方法具有重要的實用價值。事件8～事件10的重要度隨服役時間的增長并沒有產生明顯變化。

4 結 論

針對海上浮式風機基礎-塔柱系統進行了有限元分析，采用瞬態分析方法和雨流計數法得到了結構風險事件的失效概率，有效彌補了因工程數據不足引起的概率來源不足問題，增加了風險分析的準確性。另外，完成了全面的失效概率分析，進行了各事件概率重要度分析。主要結論如下：

(1) 基礎與主斜撐的連接點在風浪流聯合作用下更易出現較大應力和疲勞風險，應在實際工程中加強對該點的應力監測和安全維護。

(2) 該風機的基礎-塔柱系統整體結構風險概率較低，在服役年限內，最大風險概率約為0.000 7。在不完全維修因數為0.5的情況下，系統達到設計壽命時，其整體風險概率較不維修時下降約60%。

(3) 在服役年限內，極端環境載荷的威脅具有最高的失效概率重要度，應加強對服役海域的海況預報。隨著風機服役時間的推移，結構安全性風險的概率重要度不斷升高，建議服役時間較久的風機縮短可靠性檢驗周期，并加強結構風險評估工作。