問渠那得清如許 為有源頭活水來

馬兆兵

數(shù)學教材中的例題和習題是教材的重要組成部分，也是一些中考題的來源。我們在復習時，應從教材入手，理清知識之間的內(nèi)在聯(lián)系，既要知其然，又要知其所以然。

【原題再現(xiàn)】蘇科版八（上）95頁第21題：

在矩形紙片ABCD中，AB=6，BC=8。（1）將矩形紙片沿BD折疊，點A落在點E處（如圖1），設(shè)DE與BC相交于點F，求BF的長；（2）將矩形紙片折疊，使點B與點D重合（如圖2），求折痕GH的長。

圖1

圖2

【解析】（1）設(shè)BF=x，由題意可得，∠FDB=∠ADB=∠FBD，即DF=BF=x，則CF=8-x。則在Rt△CDF中，CF2+CD2=DF2，即（8-x）2+62=x2，解

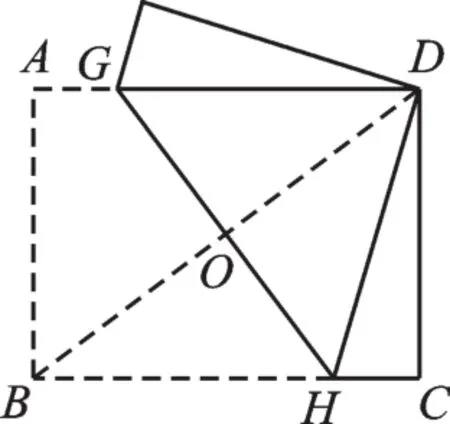
圖3

【點評】本題給出了兩種不同形式的折疊，都能體現(xiàn)折疊的基本性質(zhì)：折疊只改變了圖形的位置，沒有改變圖形的形狀、大小。在解決問題時，需要充分利用已知條件，合理使用平行線性質(zhì)、等腰三角形性質(zhì)、勾股定理等知識。

考點一 折疊中的對應點的坐標

例1 如圖4，四邊形OABC是矩形，點A的坐標為（8，0），點C的坐標為（0，4），把矩形OABC沿OB折疊，點C落在點D處，則點D的坐標為 。

圖4

圖5

【解析】如圖5，由折疊得：∠CBO=∠DBO，∵矩形ABCO，∴BC∥OA，∴∠CBO=∠BOA，∴∠DBO=∠BOA，∴BE=OE。

在△ODE和△BAE中，

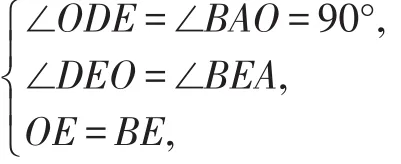
∴△ODE≌△BAE（AAS），

∴AE=DE。

設(shè)DE=AE=x，則有OE=BE=8-x。

在Rt△ODE中，根據(jù)勾股定理得：OD2+DE2=OE2，即42+x2=（8-x）2，解得：x=3，即DE=3，OE=5。

【點評】求點的坐標，關(guān)鍵在求點到坐標軸的距離。常利用勾股定理或等積法求有關(guān)線段的長。

考點二 折疊中的三角函數(shù)問題

例2 如圖6，矩形紙片ABCD，AB=4，BC=3，點P在BC邊上，將△CDP沿DP折疊，點C落在點E處，PE、DE分別交AB于點O、F，且

OP=OF，則cos∠ADF的值為（ ）。

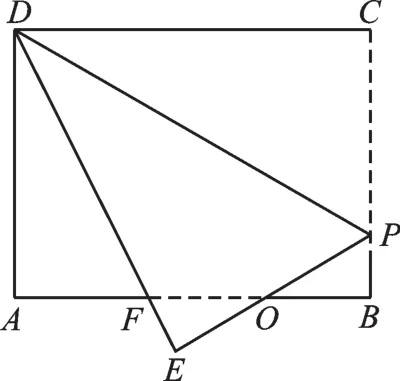
圖6

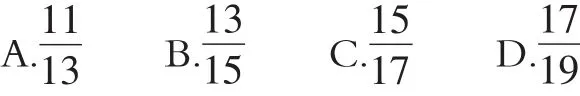
【解析】根據(jù)折疊，可知：△DCP≌△DEP，∴DC=DE=4，CP=EP。

在△OEF和△OBP中，

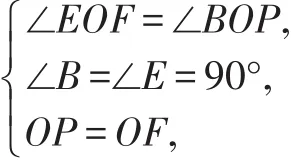
∴△OEF≌△OBP（AAS），

∴OE=OB，EF=BP。

設(shè) EF=x，則 BP=x，DF=DE-EF=4-x，又∵BF=OB+OF=OE+OP=PE=PC，PC=BC-BP=3-x，∴AF=AB-BF=1+x。

在Rt△DAF中，AF2+AD2=DF2，即（1+x）2+32=（4-x）2，解得：，∴DF=4-x=，∴cos

故選：C。

【點評】三角函數(shù)問題一般是在直角三角形中研究，若題目給出的不是直角三角形，可以通過作一邊上的高得到。有時也可以通過等角的性質(zhì)，將角轉(zhuǎn)換，再根據(jù)相似三角形（或全等三角形）求出對應角的三角函數(shù)值。

考點三 折疊中的最值問題

例3 如圖7，在Rt△ABC中，∠C=90°，AC=6，BC=8，點F在邊AC上，并且CF=2，點E為邊BC上的動點，將△CEF沿直線EF翻折，點C落在點P處，則點P到邊AB距離的最小值是 。

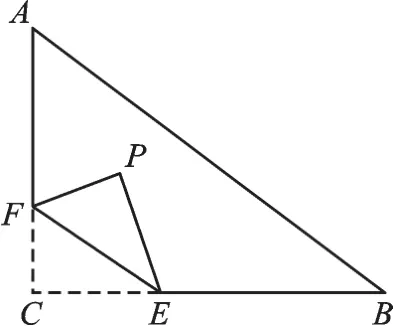
圖7

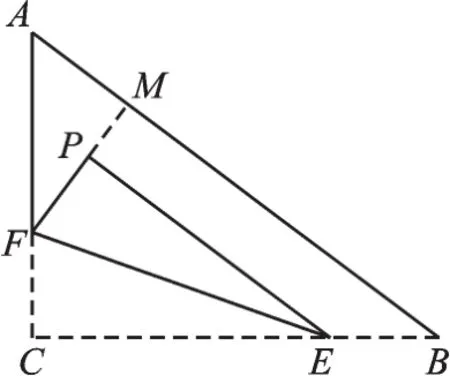
圖8

【解析】見圖8，延長FP，交AB于M，當FP⊥AB時，點P到AB的距離最小。

∵∠A=∠A，∠AMF=∠C=90°，∴△AFM∽△ABC，∴，∵CF=2，AC=6，BC=8，∴AF=4，AB= AC2+BC2=10，∴，∴FM=3.2，∵PF=CF=2，∴PM=1.2，∴點P到邊AB距離的最小值是1.2。

【點評】解題關(guān)鍵在于能正確確定點P的位置。點到線的距離就是點到線的垂直距離，因此當F、P、M在一條直線上，P到AB的距離最小。

考點四 菱形的折疊

例4 對角線長分別為6和8的菱形ABCD，如圖9所示，點O為對角線的交點，過點O折疊菱形，使B、B′兩點重合，MN是折痕。若B′M=1，則CN的長為（ ）。

A.7 B.6 C.5 D.4

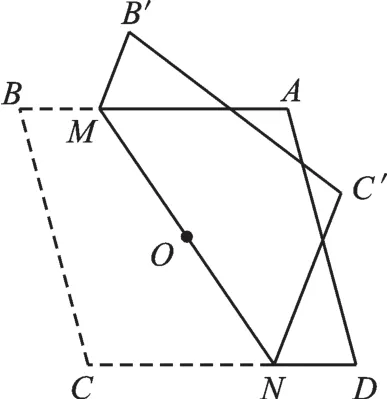
圖9

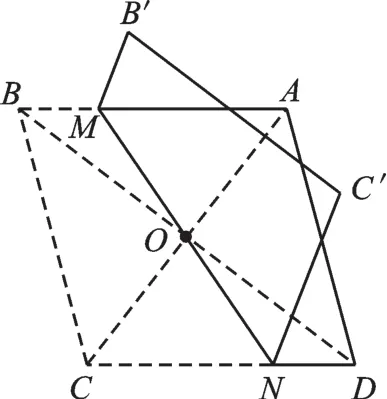
圖10

【解析】連接AC、BD，如圖10，∵點O為菱形ABCD的對角線的交點，∴OC=AC=3，OD=BD=4，∠COD=90°。

在Rt△COD中，CD=32+42=5。

∵AB∥CD，∴∠MBO=∠NDO，在△OBM

和△ODN中，

∴△OBM≌△ODN（ASA），

∴DN=BM。

∵過點O折疊菱形，使B、B′兩點重合，MN 是折痕，∴BM=B′M=1，∴DN=1，∴CN=CD-DN=5-1=4。

故選：D。

【點評】菱形折疊問題有時還需要根據(jù)菱形的一些特殊性質(zhì)如四邊相等、對角線互相垂直等解決問題。

考點五 折疊中的角度問題

例5 如圖11，將矩形ABCD沿EF折疊，使點B落在AD邊上的點G處，點C落在點H處，已知∠DGH=30°，連接BG，則∠AGB= 。

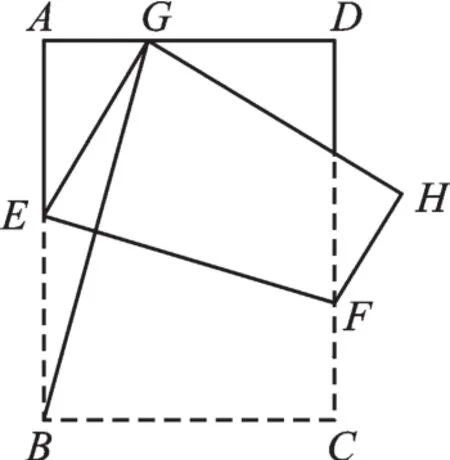
圖11

【解析】由折疊的性質(zhì)可知：GE=BE，∠EGH=∠ABC=90°，∴∠EBG=∠EGB。∴∠EGH-∠EGB=∠EBC-∠EBG，即：∠GBC=∠BGH。又∵AD∥BC，∴∠AGB=∠GBC。∴∠AGB=∠BGH。∵∠DGH=30°，∴∠AGH=150°，∴∠AGB=∠AGH=75°。故答案為：75°。

【點評】判斷折疊中對應點的連線被對稱軸垂直平分是解決此類問題的關(guān)鍵。

折疊問題只是教材習題中的冰山一角，但可以衍生出很多類型的中考試題。因此，我們在復習時，要學會回歸教材，注重“知識的形成與結(jié)論并重”，從而達到“舉一反三”“觸類旁通”的效果。