基于宏觀基本圖的城市擁堵區(qū)域優(yōu)化研究

秦山根

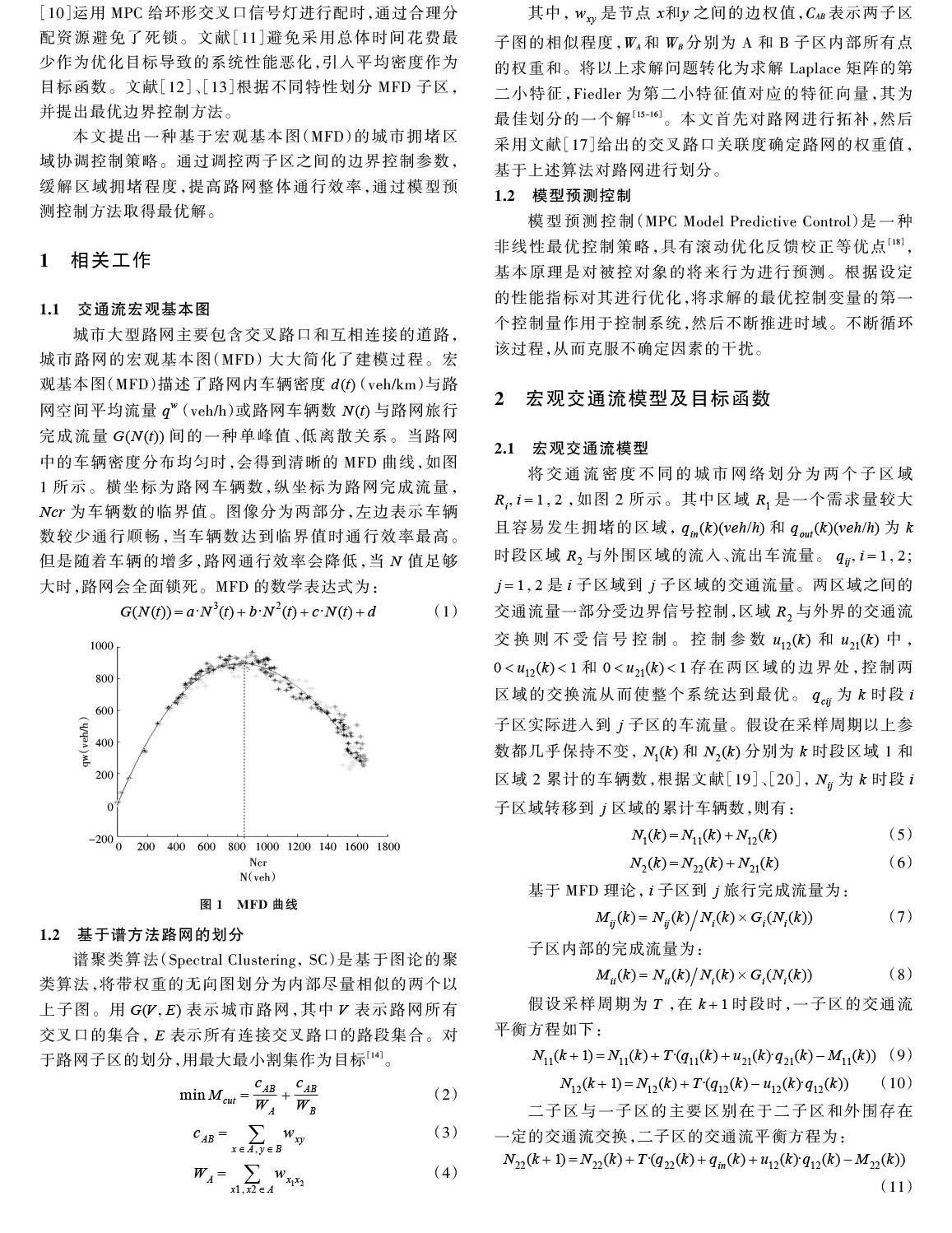
摘 要：為了解決交通高峰時段城市部分區(qū)域因需求過大而導致?lián)矶虑彝ㄐ行实拖聠栴}，設計了基于不同擁堵程度的子區(qū)域宏觀基本圖（Macroscopic fundamental diagram MFD），建立擁堵區(qū)域優(yōu)化控制模型，利用模型預測（Model Predictive Control MPC）方法獲得最優(yōu)解。根據(jù)譜聚類方法將路網劃分為擁堵與非擁堵區(qū)域，獲得清晰的MFD曲線，在此基礎上建立優(yōu)化模型，并用遺傳算法對處理過的目標函數(shù)進行求解。仿真實驗結果表明，在該模型的作用下，擁堵區(qū)域的擁堵情況得到明顯改善，區(qū)域通行能力得到了優(yōu)化。

關鍵詞：宏觀基本圖；模型預測；交通擁堵

DOI：10. 11907/rjdk. 182388

中圖分類號：TP319 文獻標識碼：A 文章編號：1672-7800（2019）005-0158-04

Abstract： In order to solve the problem of congestion and low efficiency due to excessive demand in some areas of the city during traffic peak hours， a macroscopic fundamental diagram （MFD） of sub-areas based on different congestion levels is designed to establish an optimal control model for congested areas. This problem is solved by model predictive control（MPC）. According to the spectral clustering method， the road network is divided into congested and non-congested areas， and a clear MFD curve is obtained. Based on this， an optimization model is established， and the processed target function is solved by genetic algorithm. The simulation results show that under the action of the model， the traffic volume of the road network in the congested area and the cumulative number of completed vehicles in the whole area are optimized.

Key Words： MFD； MPC； traffic congestion

0 引言

隨著社會的發(fā)展，私家車數(shù)量越來越多，城市交通擁堵問題越來越嚴重，部分區(qū)域早高峰和晚高峰時擁堵程度特別嚴重，但是外圍區(qū)域情況良好，調控城市特定區(qū)域的擁堵問題倍受關注。

傳統(tǒng)的區(qū)域交通控制系統(tǒng)如SCOOT、SCART等[1-2]很難解決飽和交通狀態(tài)下的路網交通控制問題，更加復雜的系統(tǒng)如OPAC[3]、RHODES[4]等無法圍繞某一個核心擁堵區(qū)域進行宏觀控制。城市交通擁堵都是區(qū)域性的，對于路網中的每個交叉口以及車流進行動態(tài)建模很難。與這種微觀路網建模相反，宏觀基本圖（MFD）則可很好地對區(qū)域網絡進行建模。Daganzo[5]提出了MFD模型，通過實驗數(shù)據(jù)證明了交通流參數(shù)之間的關系和MFD的基本特性，MFD成為交通控制領域一個重要理論。文獻[6]將微觀的交通流與MFD進行整合，用來限制控制策略的搜索空間，發(fā)揮了各自的優(yōu)勢。文獻[7]提出迭代學習策略，使路段平均占有率收斂到合理值。Keyvan-Ekba-tani等[8-9]基于MFD理論，提出了門限控制和魯棒控制。這些控制方法均可有效緩解擁堵區(qū)內部的交通狀況， 然而均未考慮擁堵區(qū)域外路網狀態(tài)及邊界控制對受控車輛的影響。

模型預測控制（MPC）具有滾動優(yōu)化、反饋校正的優(yōu)點，這種控制機制已經應用到交通控制的各個方面。文獻[10]運用MPC給環(huán)形交叉口信號燈進行配時，通過合理分配資源避免了死鎖。文獻[11]避免采用總體時間花費最少作為優(yōu)化目標導致的系統(tǒng)性能惡化，引入平均密度作為目標函數(shù)。文獻[12]、[13]根據(jù)不同特性劃分MFD子區(qū)，并提出最優(yōu)邊界控制方法。

本文提出一種基于宏觀基本圖（MFD）的城市擁堵區(qū)域協(xié)調控制策略。通過調控兩子區(qū)之間的邊界控制參數(shù)，緩解區(qū)域擁堵程度，提高路網整體通行效率，通過模型預測控制方法取得最優(yōu)解。

1 相關工作

1.1 交通流宏觀基本圖

2.2 控制目標與多目標函數(shù)

假設MFD為路網的固有屬性，邊界控制不影響擁堵區(qū)域內外的MFD形式。

系統(tǒng)的控制目標為增大路網輸出量，也就是使宏觀路網的旅行車輛流量最大化。為了提高車輛運行效率，需要減少交叉口的延誤時間，將路網各交叉口的平均延誤時長作為優(yōu)化目標。因此，可建立多目標函數(shù)評價路網的運行狀態(tài)。

3 實驗仿真

為檢驗以上模型效果，本文選取上海陸家嘴面積大約為4.5km2的城市中心區(qū)域進行仿真。將選取的區(qū)域地圖（見圖3）導入到仿真軟件VISSIM中。利用VISSIM的COM接口和Matlab2014聯(lián)合進行仿真，仿真時長為 5 400s。路網物理參數(shù)為：路段長度240m～460m，路段車道數(shù)為2，其中陰影區(qū)域為通過實時數(shù)據(jù)和分類算法得出的擁堵區(qū)域[R1]。兩區(qū)域的MFD擬合曲線如圖4所示，實驗結果如圖5和圖6所示，仿真結果的所有評價數(shù)據(jù)都來自VISSIM。實驗設置了固定配時方案（FC）和本文設計的邊界控制方案（PC）。

擁堵區(qū)域[R1]車輛完成流量的平均值分別為：邊界控制（PC）和固定配時（PC）為727.45（veh/h）和667.18（veh/h），優(yōu)化提高了9.03%，區(qū)域[R2]車輛完成流優(yōu)化前后的平均值為653.76（veh/h）和670.55（veh/h），優(yōu)化提高了2.5%，如圖5所示。整個區(qū)域的累計完成車輛數(shù)平均值分別在邊界控制（PC）和固定配時（FC）為9 986.2輛和9 698.4輛，優(yōu)化提高了3.0%，如圖6所示。本文模型提高了路網整體運行效率，有效緩解了城市部分區(qū)域擁堵現(xiàn)象。

4 結語

基于宏觀基本圖的擁堵區(qū)域優(yōu)化模型通過預測控制，給出了邊界交叉口的信號配時。仿真結果顯示交通網絡得到了邊界優(yōu)化控制，區(qū)域擁堵程度得到了緩解，整體路網運行效率得到了很大提升。

參考文獻：

[1] ROBERTSON D I，BRETHERTON R D.Optimizing networks of traffic signals in real time-the scoot method[J]. IEEE Transactions on Vehicular Technology， 1991， 40（1）：11-15.

[2] ？OCHOWSKA R，CELI？SKI I，SOBOTA A，et al. Selected issues of a coordinated adaptive road traffic system application within the Silesian conurbation[C]. Transport Systems Telematics Conference，2010：364-373.

[3] GARTNER N H. Development and testing of a demand-responsive strategy for traffic signal control[C].American Control Conference. IEEE， 2009：578-583.

[4] MIRCHANDANI P，HEAD L. A real-time traffic signal control system： architecture， algorithms， and analysis[J]. Transportation Research Part C， 2001， 9（6）：415-432.

[5] GEROLIMINIS N，DAGANZO C F. Existence of urban-scale macroscopic fundamental diagrams： some experimental findings[J]. Transportation Research Part B， 2008， 42（9）：759-770.

[6] CHU T，WANG J. Traffic signal control with macroscopic fundamental diagrams[C]. American Control Conference. IEEE，2015：4380-4385.

[7] DING Y，JIN S，YIN C，et al. ILC based perimeter control for an urban traffic network[C]. International Conference on Control， Automation， Robotics and Vision. IEEE， 2017：1-6.

[8] KEYVAN-EKBATANI M，KOUVELAS A，PAPAMICHAIL I，et al. Exploiting the fundamental diagram of urban networks for feedback-based gating[J]. Transportation Research Part B，2012，46（10）：1393-1403.

[9] HADDAD J，SHRAIBER A. Robust perimeter control design for an urban region[J]. Transportation Research Part B，2014（68）：315-332.

[10] 葉寶林. 城市路網交通信號協(xié)調控制理論與方法研究[D]. 杭州：浙江大學， 2015.

[11] 丁宏飛，劉碩智，秦政. 基于模型預測控制的城市快速路交通協(xié)同控制[J]. 公路交通科技，2016，33（10）：111-117.

[12] 丁恒，郭放，蔣程鑌，等. 多個MFD子區(qū)邊界協(xié)調控制方法[J]. 自動化學報，2017，43（4）：548-559.

[13] SIRMATEL I I，GEROLIMINIS N. Model predictive control of large- scale urban networks via perimeter control and route guidance actuation[C]. IEEE Conference on Decision and Control，2016：6765-6770.

[14] 高琰，谷士文，唐琎，等. 機器學習中譜聚類方法的研究[J]. 計算機科學，2007，34（2）：201-203.

[15] 李曉丹. 城市道路網絡交通小區(qū)動態(tài)劃分理論與方法研究[D]. 上海：同濟大學，2009.

[16] 馬瑩瑩，楊曉光，瀅. 基于譜方法的城市交通信號控制網絡小區(qū)劃分方法[J]. 系統(tǒng)工程理論與實踐，2010，30（12）：2290-2296.

[17] 盧凱，徐建閩，李軼舜. 基于關聯(lián)度分析的協(xié)調控制子區(qū)劃分方法[J]. 華南理工大學學報：自然科學版，2009，37（7）：6-9.

[18] 席裕庚，李德偉，林姝. 模型預測控制——現(xiàn)狀與挑戰(zhàn)[J]. 自動化學報，2013，39（3）：222-236.

[19] GEROLIMINIS N，HADDAD J，RAMEZANI M. Optimal perimeter control for two urban regions with macroscopic fundamental diagrams： a model predictive approach[J]. IEEE Transactions on Intelligent Transportation Systems，2013，14（1）：348-359.

[20] HADDAD J，GEROLIMINIS N. On the stability of traffic perimeter control in two-region urban cities[J]. Transportation Research Part B， 2012， 46（9）：1159-1176.

（責任編輯：杜能鋼）