基于機動檢測的自適應IMM目標跟蹤算法

鄧麗穎，陳 磊

(中國電子科技集團有限公司第三十八研究所，安徽 合肥 230088)

0 引 言

機動目標跟蹤是雷達數據處理中的關鍵環節，實現精確穩定的跟蹤需要有效地抑制量測誤差，精確估計目標的運動參數，其難點在于目標運動方式的不確定性[1]。若采用的運動模型與目標實際的運動模型不匹配，將導致濾波器的估計精度下降，甚至會造成濾波器發散。

根據目標不同的運動狀態，常用的運動模型有勻速運動模型、勻加速運動模型、Singer模型和當前統計模型等。對于出現轉彎、急停等高機動性能的目標，勻速和勻加速運動模型無法適用于其運動狀態。Singer模型和當前統計模型均為機動目標自適應的跟蹤算法，Singer模型把機動控制項作為相關噪聲建模，認為目標的加速度是具有指數自相關的零均值隨機過程，而當前統計模型是一種具有自適應非零均值加速度的Singer模型[2]。但如何選取正確的機動頻率是采用Singer模型和當前統計模型面臨的問題。因此單一的模型無法描述目標復雜時變的運動過程[3]。

本文提出了一種基于機動檢測的自適應交互式多模型算法，通過交互式多模型算法根據目標的機動和未機動的運動狀態自適應調整CV模型和Singer模型的模型概率，其中Singer模型參數可根據目標的強弱機動等級自適應地調整，仿真結果表明了該算法的有效性。

1 數學模型

1.1 CV模型

CV模型，即勻速運動模型。目標做勻速直線運動時，加速度為零。由于存在隨機擾動，可以將目標的加速度看作是隨機噪聲產生的結果，如下式所示：

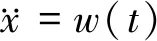
(1)

式中：w(t)為均值為0、方差為q的高斯白噪聲：

E[w(t)]=0

(2)

E[w(t)w(t+τ)]=q2δ(τ)

(3)

取系統的狀態變量為：

(4)

則系統的連續時間狀態方程為：

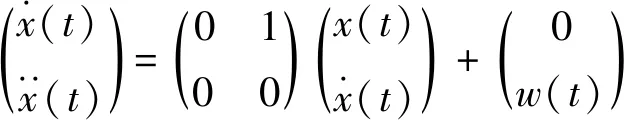
(5)

將式離散化得到系統離散時間狀態方程為：

x(k)=FCVx(k-1)+WCV

(6)

式中：FCV為CV模型狀態轉移矩陣，表達式為：

(7)

其過程噪聲WCV具有協方差QCV為：

(8)

1.2 Singer模型

Singer模型又稱為時間相關模型，它用有色噪聲對機動加速度建模。假設目標機動的加速度a(t)為一個平穩的時間相關隨機過程，其時間相關函數表達為：

(9)

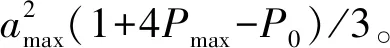
該模型采用Kalman濾波進行目標跟蹤時，需要對有色噪聲白化處理，白化后的相關函數Ra(τ)為：

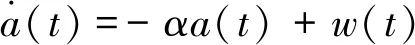
(10)

取系統的狀態變量為：

(11)

則系統的連續時間狀態方程為：

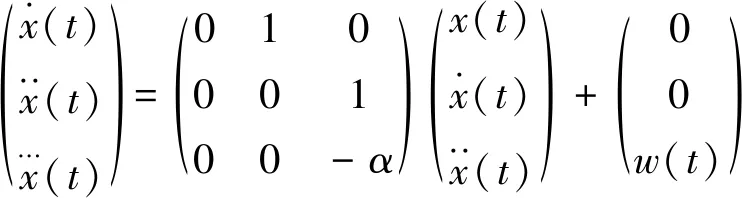
(12)

離散化得到系統離散時間狀態方程為：

x(k)=FSingerx(k-1)+WSinger

(13)

式中：FSinger為Singer模型狀態轉移矩陣，表達式為：

(14)

其過程噪聲WSinger具有協方差QSinger為：

(15)

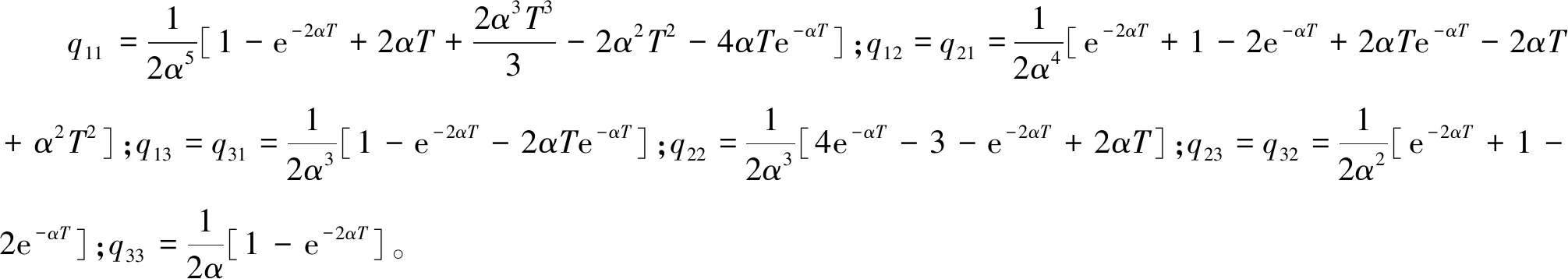
1.3 基于機動檢測的自適應參數Singer模型

Singer模型通常將機動頻率和加速度方差取為常數，若目標作不同等級的機動，固定的機動頻率和加速度方差將不能匹配于目標的真實運動情況。以機動頻率為例，當目標的實際機動頻率小于模型設定的機動頻率，跟蹤會出現延遲，導致強機動、急轉彎跟不上，進而造成目標的丟失；當目標的實際機動頻率大于模型設定的機動頻率，會引起系統的狀態誤差增大，導致跟蹤不穩定。一般通過對目標的機動檢測來實現模型參數的自適應，本文采用跟蹤濾波時的歸一化殘差，來判斷目標的機動等級，根據機動等級的強弱來自適應地調整Singer模型的機動頻率和加速度方差的取值。

采用Kalman濾波對目標進行跟蹤，取雷達站心系下XYZ方向上的位置、速度和加速度為狀態變量：

(16)

則系統的狀態方程為：

x(k)=Fx(k-1)+W

(17)

式中：F為狀態轉移矩陣；W是協方差為Q的過程噪聲。

取雷達站心極坐標系下目標的距離、方位和仰角作為量測量：

z=[RAE]T

(18)

則系統的量測方程為：

z(k)=Hx(k)+V

(19)

式中：H為量測矩陣；V是協方差為R的量測噪聲。

在k時刻系統的殘差d(k)為：

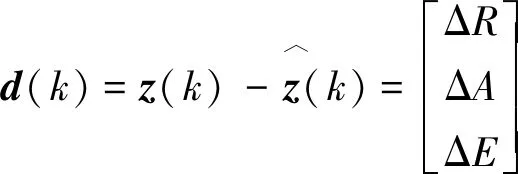
(20)

式中：ΔR、ΔA和ΔE分別為預測的距離、方位和仰角與量測之差。

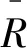
(21)

通過計算每一時刻的歸一化距離，來判斷每一時刻的機動狀態，再根據不同的機動等級來調整Singer模型的機動頻率和加速度方差的取值，從而實現模型參數的自適應調整。

2 交互式多模型算法

在進行目標跟蹤時，目標常常存在多種運動狀態，采用單一的模型往往不能匹配目標時變的運動特性，也不能保證固定的模型參數長期可靠，因此通常采用多模型的估計理論，通過建立多個模型來逼近目標復雜時變的運動過程。本文采用的是交互式多模型算法(IMM)，相比于傳統的多模型算法，IMM算法將系統視為有限狀態的Markov鏈，不同模型間通過轉移概率進行交互，模型轉移符合Markov過程。設每個子模型為線性跳躍的Markov系統：

(22)

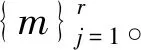
本文將CV模型和基于機動檢測的自適應參數Singer模型組成模型集，模型間的跳變滿足Markov轉移概率矩陣：

(23)

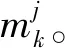
(1) 輸入交互

假設系統在k-1時刻匹配的模型為i，并在k時刻發生跳變為模型j，則此時的轉換概率為綜合Markov轉移概率以及量測條件下的后驗概率的混合概率：

μij(k-1/k-1)=

(24)

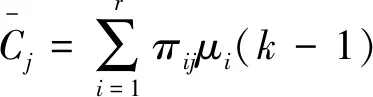
因此，可通過該轉移概率初始化每個模型在k時刻的輸入：

(25)

(26)

(2) 模型濾波

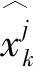
(27)

(3) 模型概率更新

采用Bayes假設檢驗法計算當前時刻模型概率，檢驗各個模型的濾波殘差。若k時刻匹配為模型j，則其模型j的濾波殘差rj(k)為零均值、方差為Sj(k)的高斯白噪聲，似然函數可表示為：

(28)

那么k時刻匹配為模型j的概率為：

(29)

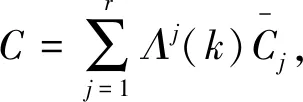
(4) 輸出綜合

將各子模型的估計結果進行加權融合可得到系統最終的狀態估計：

(30)

(31)

3 仿真研究

假設目標在XY平面內做水平機動，目標的初始方位30°，初始斜距15 km，初始速度為400 m/s，過正北向西南方向飛行。目標仿真時間150 s，在0～70 s和110～150 s內做勻速直線運動，在70～110 s內發生轉彎，最大機動加速度為9g，最大徑向速度為600 m/s。采樣的數據率1 Hz，仿真的軌跡如圖1所示。

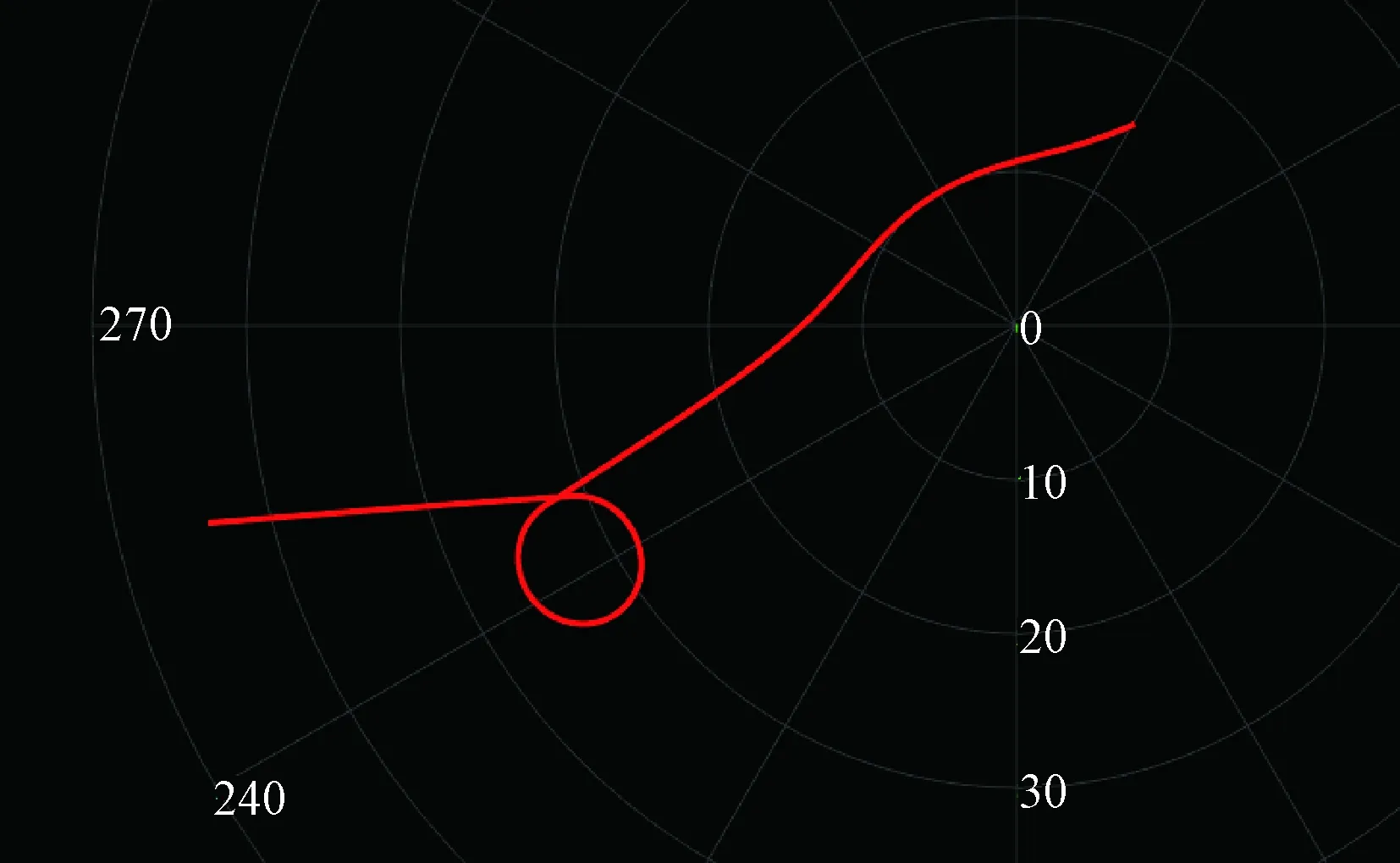
圖1 仿真目標真實軌跡

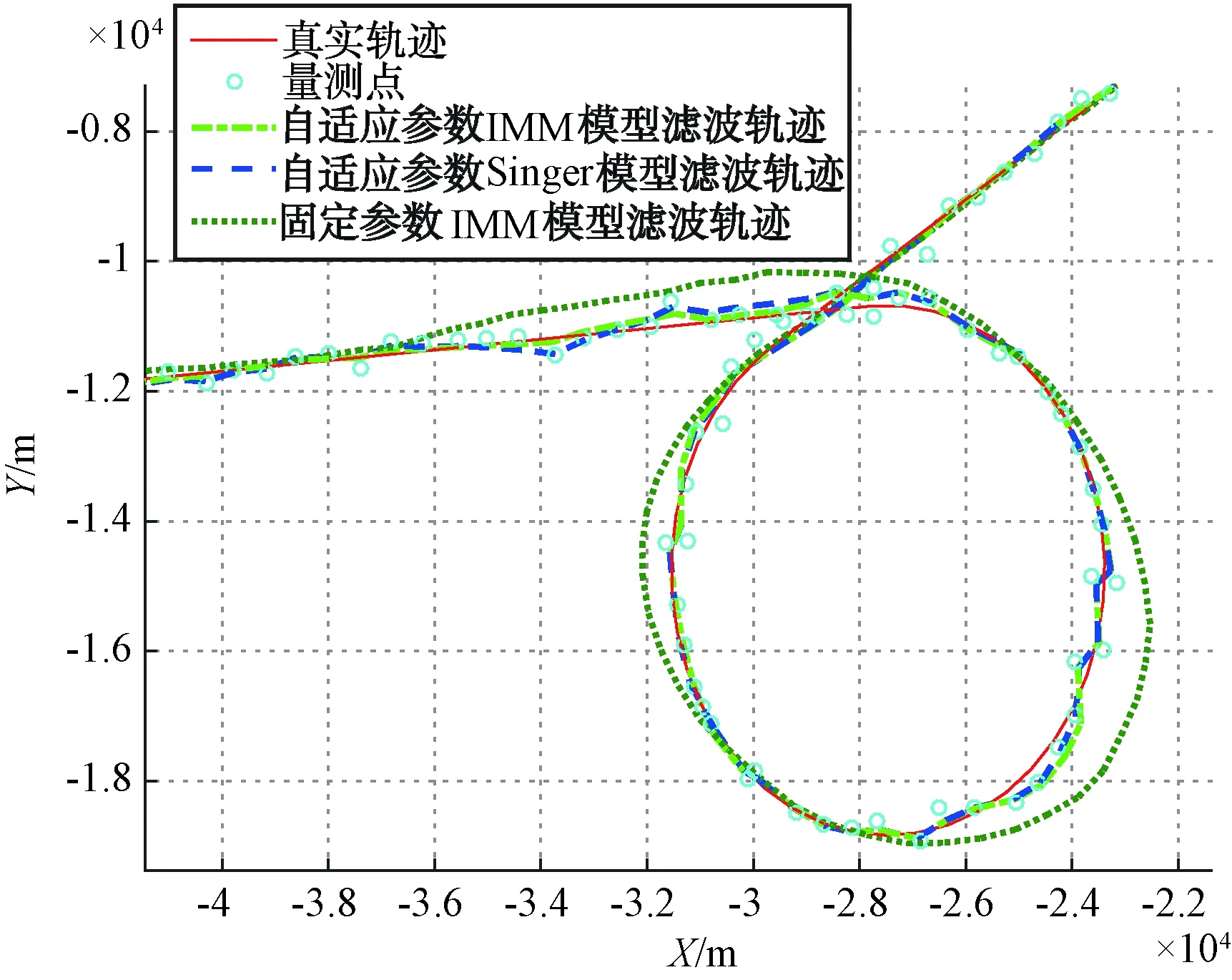
圖2 不同算法濾波點軌跡

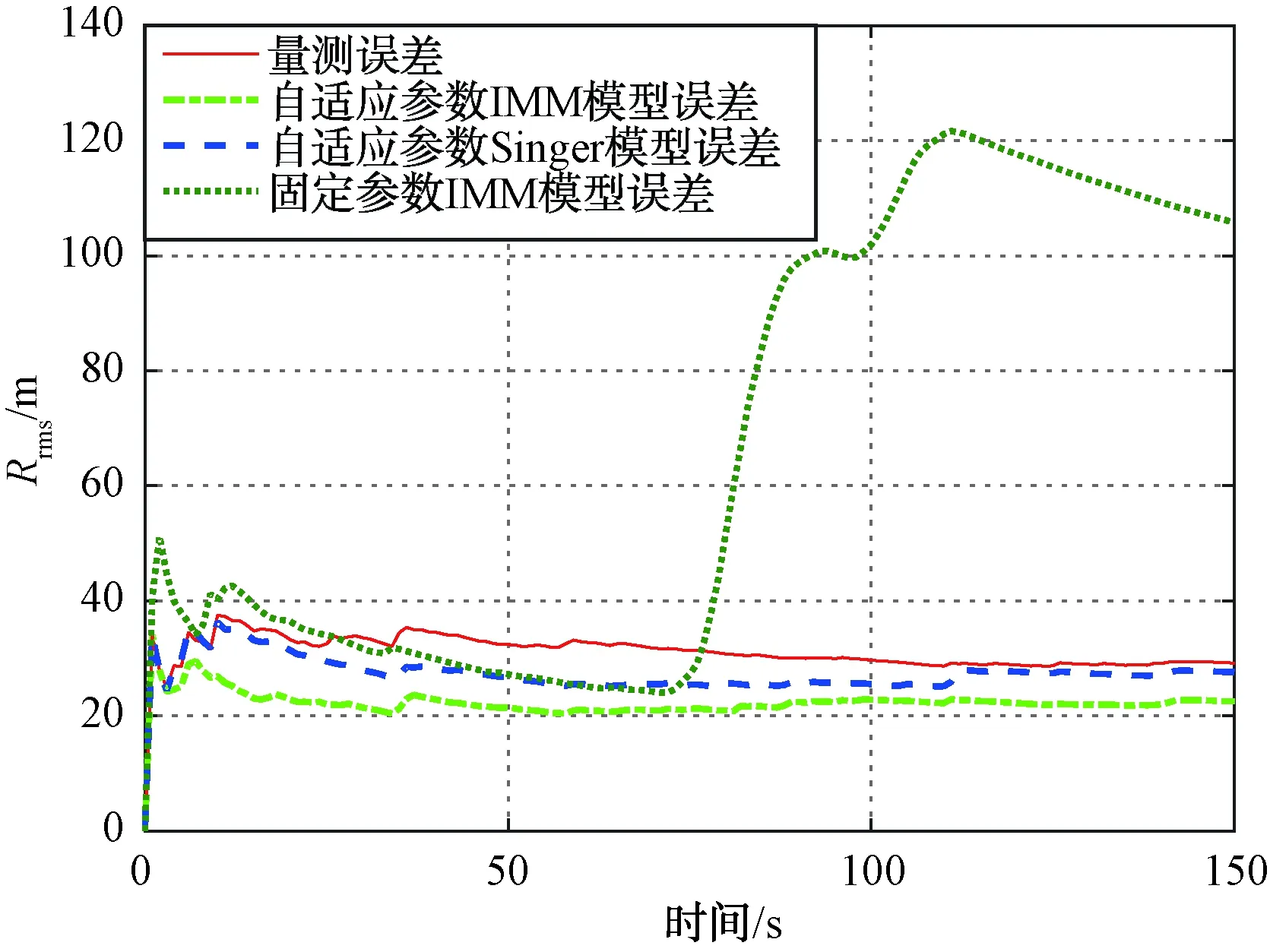
圖3 不同算法距離均方根誤差比較圖

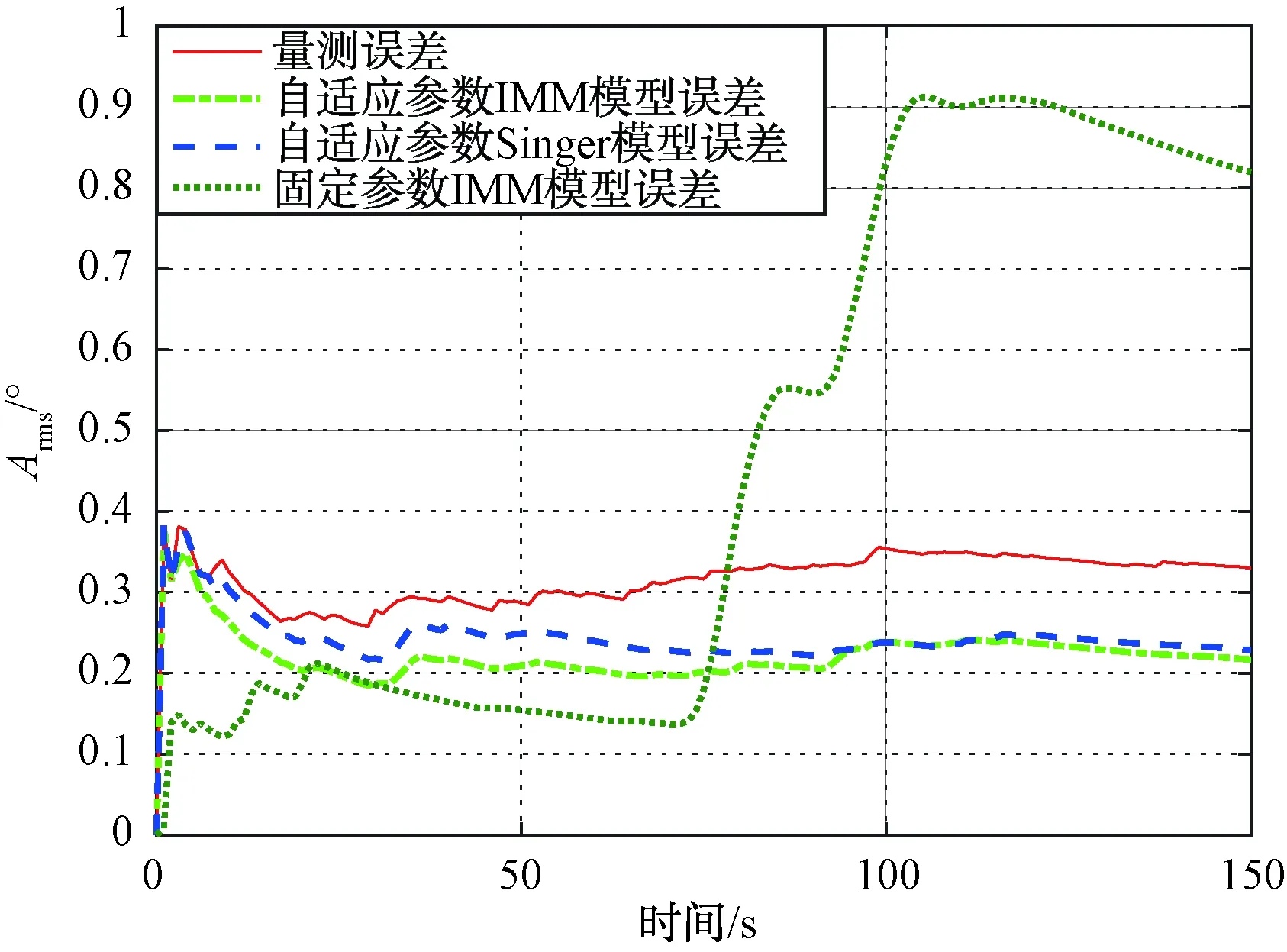
圖4 不同算法方位均方根誤差比較圖

由圖2可得，采用固定參數的IMM模型在70 s目標開始機動時，跟蹤結果出現延遲，跟不上目標的機動轉彎，距離和方位的均方根誤差也開始發散，最終的距離均方根誤差為105.829 3 m，方位均方根誤差為0.822 3°。這是因為在70 s時目標的機動性能增強，目標實際機動頻率小于模型中設定的機動頻率，導致機動轉彎跟不上。因此固定參數的IMM模型，不能隨著目標的機動狀態實時地調整模型參數，無法對機動性能發生改變的目標進行穩定跟蹤。

當采用基于機動檢測的自適應IMM算法時，相比于單個Singer模型算法的跟蹤結果，IMM模型的跟蹤更穩定，如圖3、圖4及表1所示。其估計的距離和方位的均方根誤差都小于單個Singer模型算法的均方根誤差。這是因為IMM模型中包含了CV模型和Singer模型，能根據目標的運動狀態，實時地調整模型概率，選擇與目標運動更匹配的模型。綜上，相比于單個Singer模型算法和固定參數IMM算法，本文提出的基于機動檢測的自適應參數IMM算法的跟蹤結果更好。

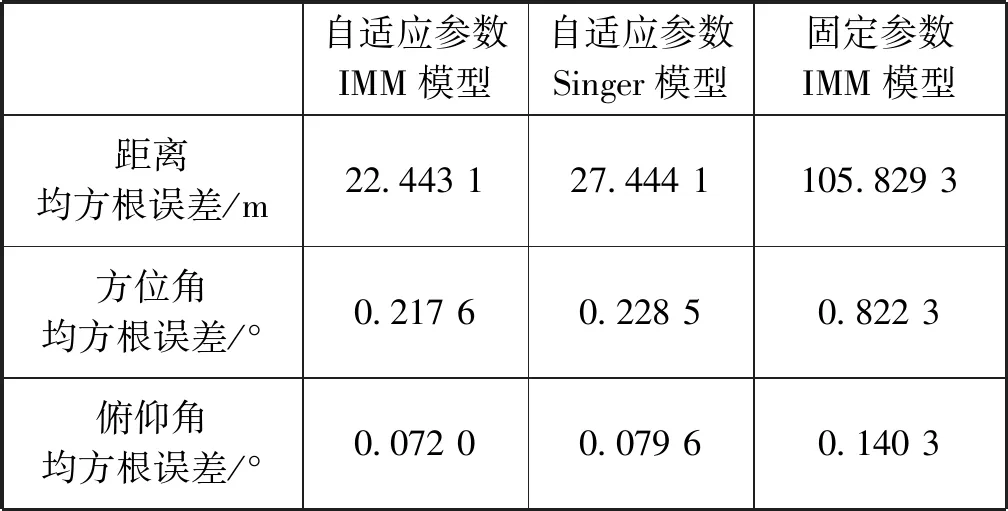
表1 不同算法跟蹤結果均方根誤差表

4 結 論

本文采用了一種基于機動檢測的自適應交互式多模型算法，通過IMM算法根據目標的機動和未機動的運動狀態自適應調整CV模型和Singer模型的模型概率。同時，針對目標機動時，存在不同的機動等級這一問題，采用基于歸一化殘差的機動等級判斷，根據目標的強弱機動等級自適應地調整Singer模型的機動頻率和加速度方差的取值，有效地提高了機動目標的跟蹤精度，實現了機動目標的穩定跟蹤。