矩形法蘭孔孔口模態輻射阻抗的計算與分析?

李家柱 葉望青 鐘秤平 陳 劍 劉 策

(1 合肥工業大學機械工程學院噪聲振動工程研究所 合肥 230009)

(2 安徽省汽車NVH 工程技術研究中心 合肥 230009)

(3 江西省汽車噪聲與振動重點實驗室 南昌 330001)

0 引言

孔口模態輻射阻抗的計算是矩形法蘭孔聲傳遞損失(Transmission loss, TL)計算的基礎，是開展大尺寸百葉窗隔聲量計算的關鍵環節。大尺寸百葉窗結構在建筑物外立面、暖通系統以及高鐵減載式聲屏障等領域應用廣泛。矩形法蘭孔孔口模態輻射阻抗表達式是包含半空間格林函數和兩組模態振型的四重積分，該積分存在奇異點，現有的高階積分算法和計算軟件無法直接求解[1]。對于這類問題，多數學者通過坐標變換將積分降為三重或二重積分，然后采用高斯求積來求解[2?5]。這種方法實現了積分的精確求解，但在積分變換后，表達式需根據相應的階次進行討論，且高斯求積方法雖較成熟，但并非MATLAB 等軟件的內置函數，仍需編寫高斯求積程序。Sha 等[1]則在將四重積分降為二重積分后，將結構劃分為網格，利用邊界條件、波數近似和傅里葉變換等方法來加速求解模態輻射阻抗，該方法需根據結構的尺寸、波數等參數改變網格大小，計算過程較復雜且計算速度不夠理想。Li 等[6?7]、沈蘇等[8]和Leppington 等[9]等通過坐標變換、參數討論等方法將這類積分降為一重積分，簡化了積分最終的求解表達式并提高了計算速度。Davy等[10]在將四重積分降為一重積分的基礎上，通過改寫最終表達式消除了奇異積分的影響。然而，這類將四重積分降為一重積分的方法推導過程復雜且需進行參數討論，如果初始的模態輻射阻抗表達式與文獻中的表達式有差異，就需重新推導，對理論知識要求較高且工作量大。

鑒于此，本文在吸收以上學者成果的基礎上，通過坐標變換將四重積分轉換為二重積分并消除奇異積分，且將該過程直接采用MATLAB 的內置函數來實現。在實現四重積分求解的基礎上，通過詳細計算和對比，驗證方法的正確性，最后分析矩形法蘭孔孔口模態輻射阻抗的性質。

1 矩形法蘭孔孔口模態輻射阻抗計算

1.1 矩形法蘭孔孔口模態輻射阻抗表達式

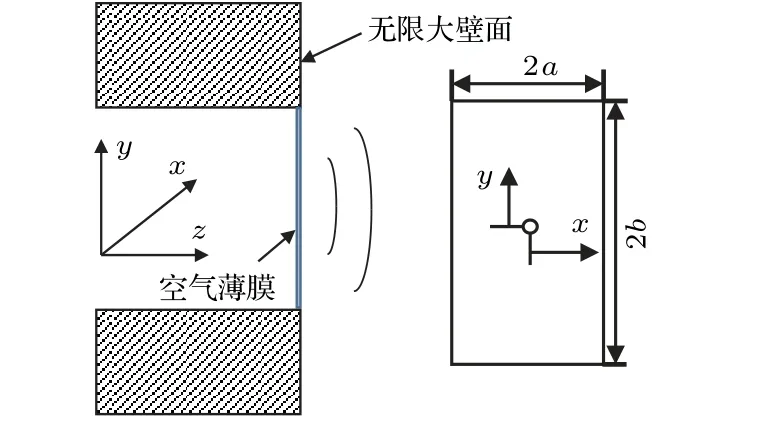
圖1 矩形法蘭孔示意圖Fig.1 Schematic diagram of flanged rectangular aperture

聲源表面的聲壓與振速的比值稱為聲源的輻射阻抗[11]。圖1為矩形法蘭孔示意圖，該孔孔口處為無限大壁面形成的半空間，孔口的振動單元可視為空氣薄膜，由于受孔口約束，空氣薄膜的四邊僅有圖1所示的z向平動自由度，其振動模態對應孔口截面模態。空氣薄膜各階振動模態對應的輻射阻抗即為矩形法蘭孔孔口模態輻射阻抗，其表達式為[5]

式(1)中，j為虛數單位，kf和Zf分別為波數和聲傳播介質的特征阻抗，本文以空氣為聲傳播介質，則Zf為空氣的特征阻抗，?mn(x,y)和?pq(x0,y0) 分別為空氣薄膜的(m,n)和(p,q)階模態的振型，表達式分別為

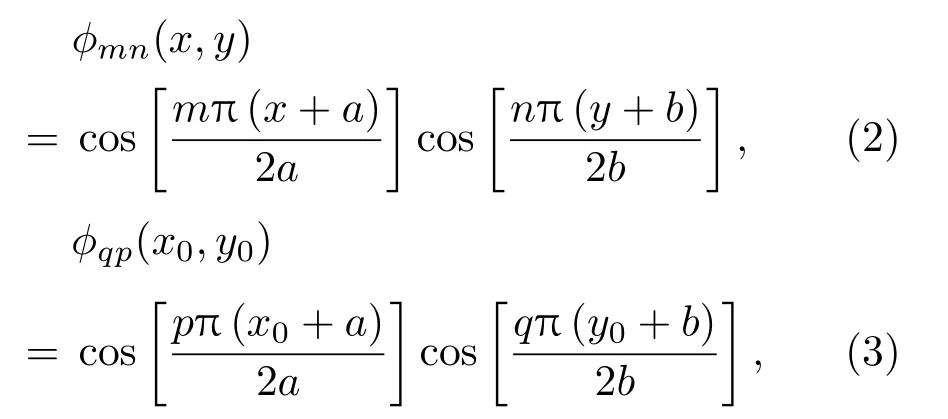
G(x,y,x0,y0)為半空間格林函數，其表達式為

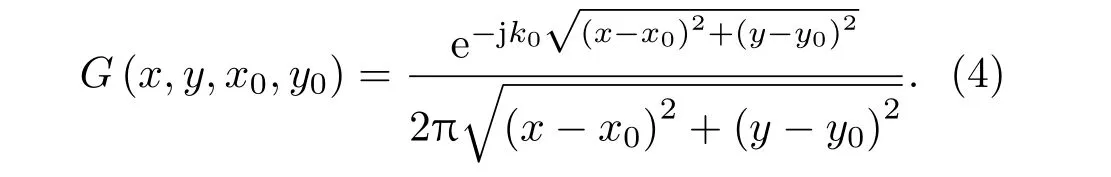
將 式(2)～(4)以 及S= 4ab代 入 式(1)可 得(m,n,p,q)階模態輻射阻抗表達式為

1.2 積分變換

式(5)是以x0、y0、x、y為積分變量的四重積分，積分區間分別為(?a,a)、(?b,b)、(?a,a)、(?b,b)，在x=x0且y=y0處，積分函數趨于無窮大，無法直接計算。為求解該積分，采用換元法，令

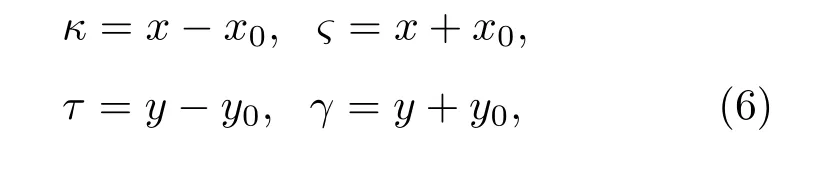
可得

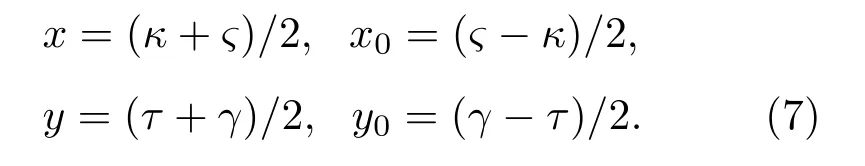
雅可比矩陣為

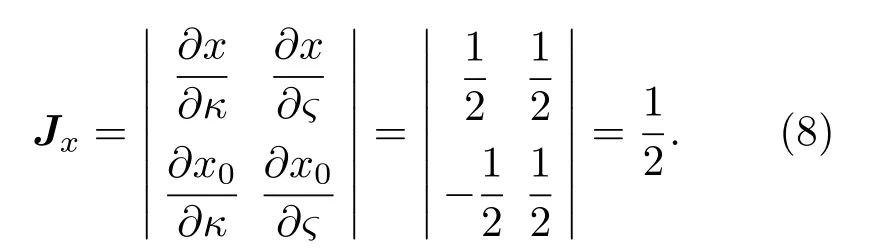
同理，Jy=1/2，此時式(5)變換為

式(9)中：

式(10)～(13)均可對ζ和γ積出解析表達式，式(9)將被轉換為四個以κ和τ為積分變量的二重積分之和。然而，當κ和τ趨于零時依然會造成積分中格林函數分母趨于零，該積分存在奇異性，需做一次極坐標變換，令：

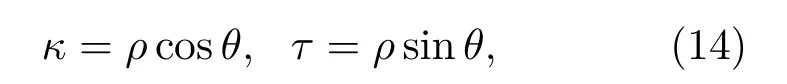
變換后的式(9)被轉換為極坐標下的二重積分，該積分可直接使用MATLAB內置的數值積分函數求解，無需采用高斯求積或對模態階次進行討論。

1.3 MATLAB求解

第1.2 節所述過程可在MATLAB中完成，主要有以下幾步：

(1) 根據式(2)～(4)，在MATLAB 中定義模態振型函數?mn(x,y)、?pq(x0,y0)以及半空間格林函數G(x,y,x0,y0)。

(2) 將變量代換式(7)帶入第(1)步定義的函數，得到變量代換后的模態振型表達式和半空間格林函數表達式。

(3) 將變量代換后的模態振型和半空間格林函數表達式代入式(5)，即得到新的模態輻射阻抗表達式(9)，要對式(9)求解，需分別對式(10)～(13)求定積分。

(4) 在MATLAB 中 采 用int 函 數 對 式(10)～(13)中的變量ζ和γ求定積分，將式(10)～(13)由四重積分轉換為僅含變量κ和τ的二重積分，此步在MATLAB中可積出解析表達式。

(5) 降維后的式(10)～(13)由于包含半空間格林函數而存在奇異性，此時在MATLAB 中根據式(14)進行極坐標變換，消除奇異積分，得到極坐標下的積分表達式。

(6) 最后利用MATLAB積分函數quad2d分別對降維和極坐標變換后的式(10)～(13)求數值積分，將式(10)～(13)求解結果代入式(9)即可求得矩形法蘭孔孔口模態輻射阻抗。

2 計算結果驗證

2.1 (0,0,0,0)階模態輻射阻抗驗證

矩形法蘭孔孔口的(0,0,0,0)階模態輻射阻抗就是矩形活塞聲源的輻射阻抗，矩形活塞聲源輻射阻抗表達式和相關計算數據可在文獻[12]中查閱。如圖2所示，法蘭孔孔口尺寸為長寬均為1 m 的正方形，圖2中Z(0,0,0,0)為(0,0,0,0)階模態輻射阻抗，Z0為空氣的特征阻抗，Z(0,0,0,0)/Z0為歸一化的模態輻射阻抗，k為波數，req為等效半徑由圖2可知，本方法算得的(0,0,0,0)階模態輻射阻抗與矩形活塞聲源輻射阻抗實部和虛部一致性很好，說明本方法計算(0,0,0,0)階模態輻射阻抗是正確的。

圖2 (0,0,0,0)階模態輻射阻抗驗證Fig.2 Radiation impedance validation of order(0,0,0,0)

2.2 高階模態輻射阻抗驗證

由于高階模態輻射阻抗難以通過仿真或實驗直接得到，因此本文將模態輻射阻抗計算方法代入矩形法蘭孔聲傳遞損失計算中來。通過代入本文阻抗計算方法的Superposition 法與Sgard 等[5]、聲學有限元法以及實驗[13]的對比，間接驗證本方法的正確性。

矩形法蘭孔的聲傳遞率與其孔口模態輻射阻抗的關系為[13]

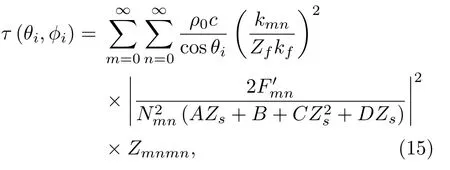
式(15)中，Zmnmn為孔口第(m,n,m,n)階模態輻射阻抗，該式已利用本文的結論之一：互模態輻射阻抗相比于自模態輻射阻抗在多數計算中可以忽略不計的性質進行了簡化，只計算了自模態輻射阻抗部分。關于孔口模態輻射阻抗性質的分析將在本文后續小節中加以論述。

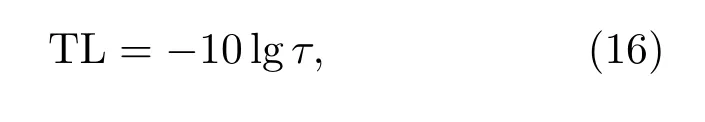
聲傳遞損失與聲傳遞率的關系為[13]從而可以根據式(16)求得矩形法蘭孔的聲傳遞損失，式(15)和式(16)中部分參數的具體描述請見參考文獻[13]。

圖3和圖4對比了代入本文阻抗計算方法的Superposition法[13]和Sgard等[5]方法的計算結果，矩形孔尺寸均為Lx=0.4 m，Ly=0.2 m，Lz=0.3 m。圖3為法向入射時的聲傳遞損失，圖4是入射角度為斜45?時的聲傳遞損失。圖3中Sgard 等的數據為采用其論文中的算法計算得到，經對比二者幾乎相等。圖4中Sgard 等的數據為直接從其論文的圖中提取出來，略微存在一定誤差，這主要是提取數據的誤差造成的。

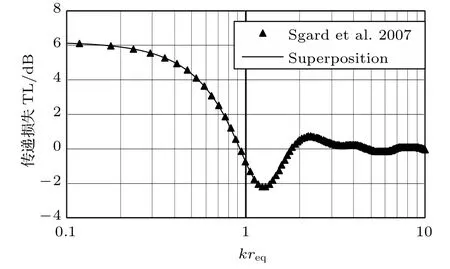
圖3 法向入射條件下矩形孔聲傳遞損失驗證Fig.3 TL validation of a rectangular aperture with normal incident

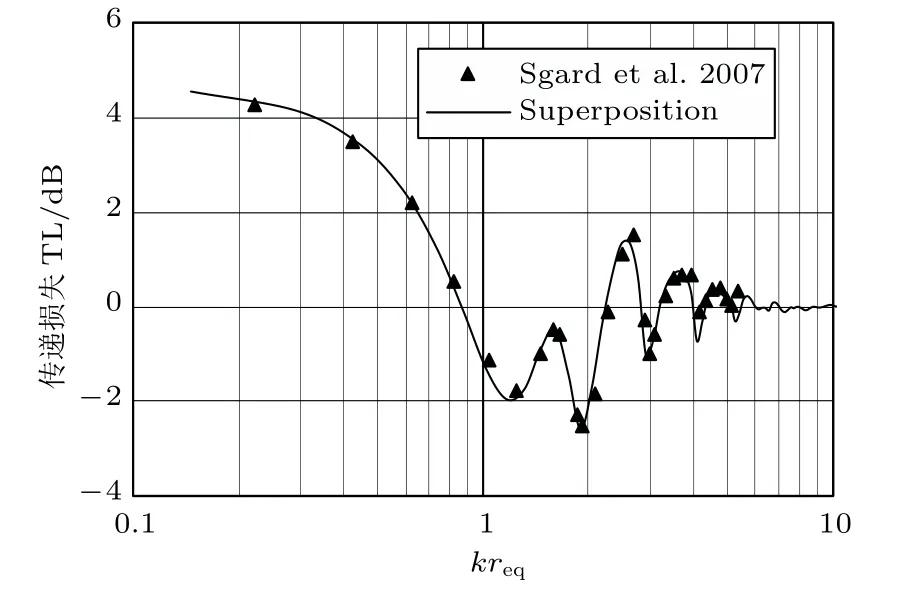
圖4 傾斜入射條件下矩形孔聲傳遞損失驗證Fig.4 TL validation of a rectangular aperture with oblique incident

圖5為散射聲場中代入本文阻抗計算方法的Superposition 法[13]、Trompette 等[14]的實驗以及聲學有限元法的對比，矩形孔尺寸為Lx=0.06 m，Ly=0.13 m，Lz=0.3 m。觀察圖5可知，三條曲線一致性較好。

以上通過將本文模態輻射阻抗計算方法代入Superposition 法， 與Sgard 等的計算結果、Trompette 等的實驗結果以及聲學有限元法的結果對比，取得了很好的一致性，從側面驗證了本方法計算高階模態輻射阻抗的正確性。

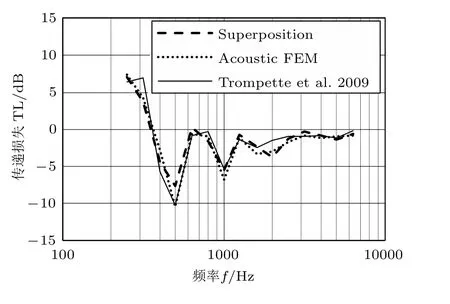
圖5 散射聲場中矩形孔聲傳遞損失對比Fig.5 TL validation of a rectangular aperture in diffuse acoustic field

3 計算結果分析

3.1 自模態輻射阻抗分析

當式(1)中m=p或n=q時的模態輻射阻抗稱為自模態輻射阻抗，圖6和圖7為孔口邊長為1 m的正方形法蘭孔孔口的前7 階自模態輻射阻抗實部和虛部的對比。

觀察圖6和圖7，可得如下結論：

(1)隨著模態階次的增加，自模態輻射阻和自模態輻射抗的峰值總體呈減小趨勢，但不是單調遞減的，高階次的峰值可能高于低階次的峰值。

(2)隨著模態階次的增加，自模態輻射阻和自模態輻射抗的峰值對應的kreq均逐漸增大，由于req為等效半徑，為常數，即對應的波數k增大，亦即對應的頻率逐漸增大。

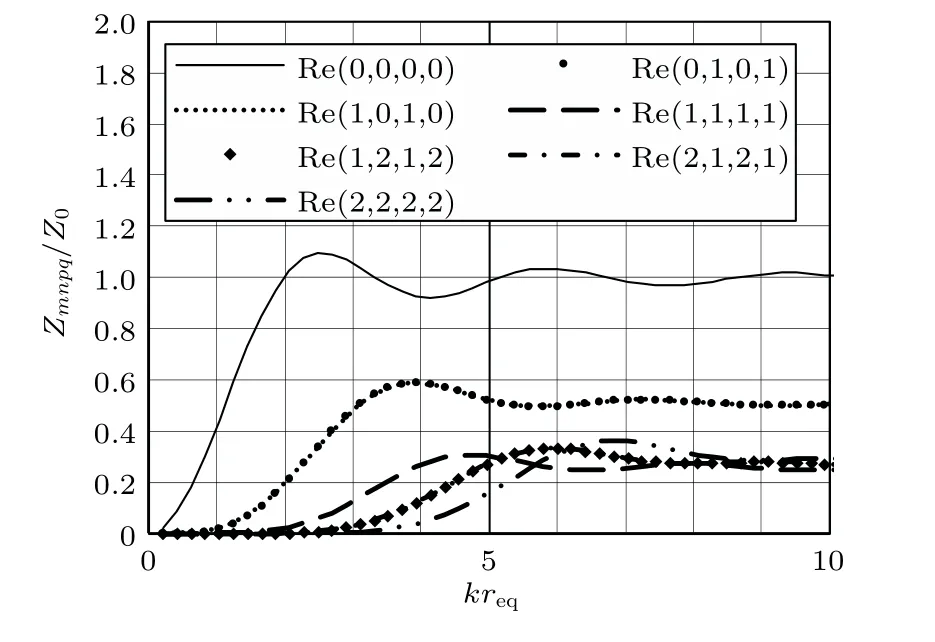
圖6 自模態輻射阻對比(Lx = 1 m、Ly = 1 m)Fig.6 Resistance comparison of self-modal radiation impedance(Lx = 1 m、Ly = 1 m)

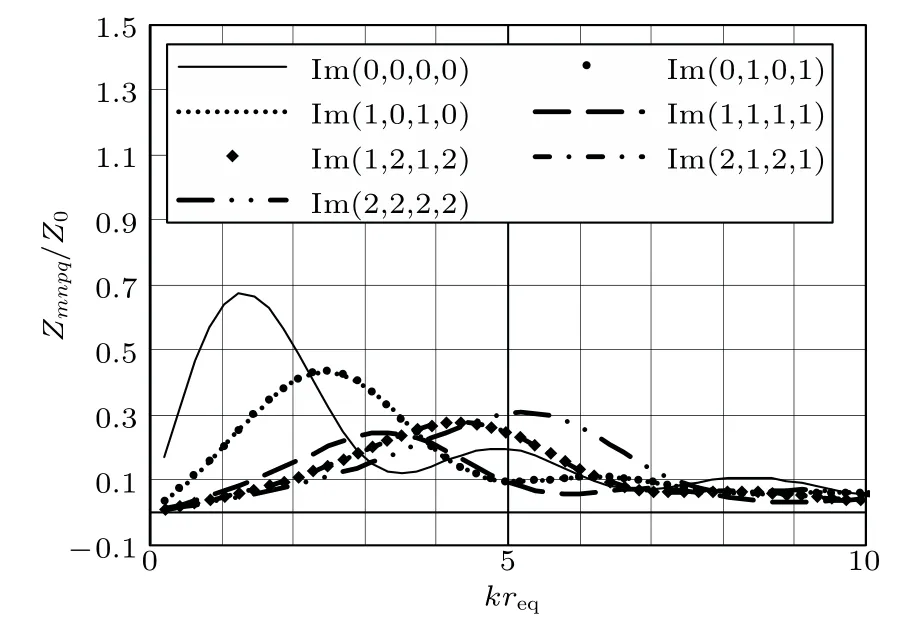
圖7 自模態輻射抗對比(Lx =1 m、Ly =1 m)Fig.7 Reactance comparison of self-modal radiation impedance(Lx =1 m、Ly =1 m)

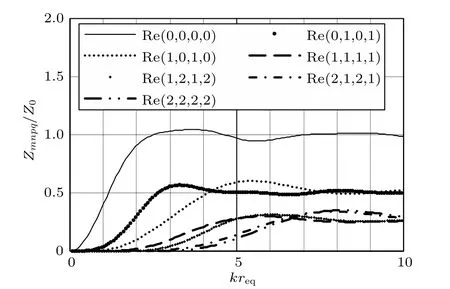
圖8 自模態輻射阻對比(Lx = 0.5 m、Ly = 1 m)Fig.8 Resistance comparison of self-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

圖9 自模態輻射抗對比(Lx = 0.5 m、Ly = 1 m)Fig.9 Reactance comparison of self-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

(3)孔口形狀為正方形時，由于對稱性，(m,n,m,n)與(n,m,n,m) 階自模態輻射阻和自模態輻射抗相等。

進一步，選取孔口邊長分別為Lx= 0.5 m、Ly=1 m的矩形法蘭孔，計算其孔口模態輻射阻抗并分析其規律。

觀察圖8和圖9，并結合圖6和圖7可知，當法蘭孔孔口形狀為長方形時，其模態輻射阻抗的性質與孔口形狀為正方形時相似。不同之處在于，其不具有(m,n,m,n)與(n,m,n,m)階模態輻射阻和模態輻射抗相等的對稱性，是因為長方形的邊長不相等。

3.2 互模態輻射阻抗分析

(1)四個階次的互模態輻射阻和輻射抗的峰值相比于自模態輻射阻和輻射抗的峰值均小很多，峰值最大的(1,2,3,4)階互模態輻射阻抗也比自模態輻射阻抗小1～2個數量級。

(2)由圖10、 圖11 和表1可知， 另三階比(1,2,3,4)階模態輻射阻抗小多個數量級。

圖10 互模態輻射阻對比(Lx = 0.5 m、Ly = 1 m)Fig.10 Resistance comparison of cross-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

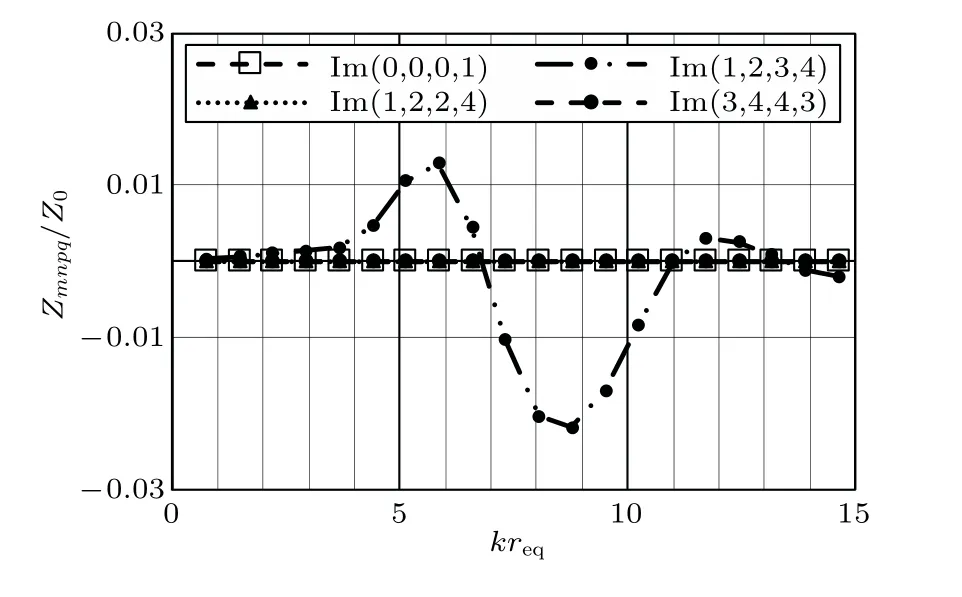
圖11 互模態輻射抗對比(Lx = 0.5 m、Ly = 1 m)Fig.11 Reactance comparison of cross-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

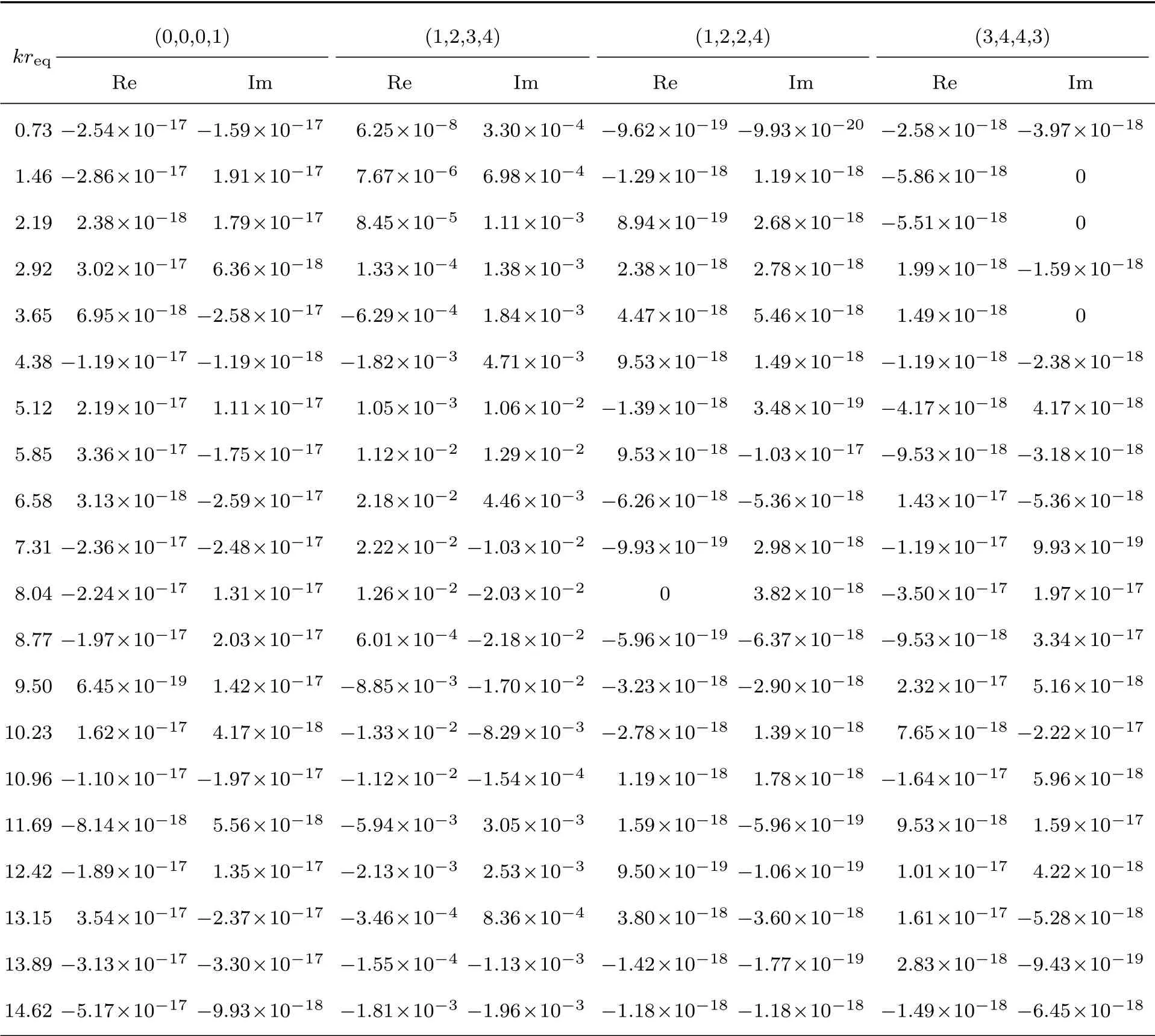
表1 互模態輻射阻抗對比Table1 Comparison of cross-modal radiation impedance

4 結論

論文詳細闡述了矩形法蘭孔孔口模態輻射阻抗積分表達式坐標變換的過程及其在MATLAB中的實現方法，對計算結果進行了驗證并分析了模態輻射阻抗的性質，結論如下：

(1)通過坐標變換將四重積分轉換為二重積分并消除了奇異積分，且將計算過程直接利用MATLAB 軟件的內置函數實現，不再需要推導公式且不再需要根據模態階次討論模態輻射阻抗的具體表達式，顯著降低了積分求解的復雜程度。

(2)隨著模態階次的增加，自模態輻射阻抗峰值總體呈減小趨勢但并非單調遞減，峰值對應的頻率逐漸增大。

(3)自模態輻射阻抗顯著大于互模態輻射阻抗，往往相差多個數量級，結合實際情況可只計算自模態輻射阻抗部分，以顯著降低計算工作量、提高計算速度。