基于數據庫進行乏燃料鑒別的多元統計分析研究

蘇佳杭 伍鈞 胡思得

1) (中國工程物理研究院研究生院,北京 100088)

2) (中國工程物理研究院戰略研究中心,北京 100088)

3) (中國工程物理研究院,北京 100088)

近年來,隨著國際核軍控形勢的變化,包含防擴散、防核恐及核安保的多邊國際軍控合作越來越受到重視.核取證技術作為防擴散、防核恐及核安保的一項核心技術,在對涉核非法活動的威懾、阻止以及響應方面具有重要作用,值得深入研究.目前針對核取證技術的研究較多,主要集中于材料的表征和數據的解讀.其中解讀作為核取證研究技術中最重要的一環,所面對的對象是多種多樣的,包括鈾礦石、黃餅、核燃料、乏燃料等,而其中乏燃料由于其潛在的威脅越來越受到重視.本文聚焦于在核取證場景中利用多元統計分析方法進行乏燃料鑒別的研究,主要是利用因子分析、判別分析和回歸分析方法對乏燃料組分進行分析,研究各方法的適用范圍,并為未來可能的利用數據庫進行乏燃料鑒別的工作提供理論依據與可行方案,為相關核取證溯源工作的順利開展提供支撐.

1 引 言

核取證學是對截獲的非法販賣的核材料或放射性物質以及其任何相關材料進行的分析,為核歸屬分析提供證據[1].核取證學是在核擴散日益嚴峻的背景下發展起來的,通過核取證學與行政法律手段的結合,可以幫助國際社會在源頭及路徑上控制核擴散與核恐怖活動.冷戰結束以后,核走私事件增多,核取證學開始受到初步重視;近些年,隨著國際恐怖主義威脅增加,核取證學開始應用于可能的核恐怖爆炸的樣品的取證分析,以此獲得核材料的識別特征,以及它們的工業加工過程,為溯源提供重要依據.因此,核取證學更加受到重視,越來越多的國家開始進行核取證學的研究與合作[2].

目前針對核取證技術的研究較多,主要集中于材料的表征和數據的解讀.“表征”是為了確定放射性證據及相關證據的性質.基本表征給出放射性物質(包括主要成分、次要成分和微量成分)的全部元素分析結果.而“解讀”則是將材料表征與生產歷史進行關聯的過程,目標是確定生產的方法和時間,是核取證學實驗室的最終產品[1].相比較而言,表征多是應用實驗室測量技術,而解讀則涉及更為廣泛的方法,也是目前核取證研究的熱門方向.解讀將經表征過程后有用的數據(通常稱之為“識別標志”)進行處理,以還原與材料來源相關的信息.識別標志通常可分為兩類,預測型和比較型[3].預測型識別標志是基于物理、化學以及工程等相關專業知識發現的材料特征,而比較型識別標志是基于對有問題的樣品和已知樣品的材料特征的比較而發展的.之前的許多研究中,一直試圖通過尋找合適的核素或核素對特征(預測型)來表征未知核材料的來源信息,但很多情況下結果并不盡如人意,原因是理論上求出的差別很難在現實測量中給出高置信的結論.

而隨著國際原子能機構(International Atomic Energy Agency)推動核取證數據庫的建立[4],基于數據庫的利用多元統計方法表征未知核材料(鈾礦石、黃餅、UF6、鈾燃料塊以及乏燃料等)來源信息的研究日趨活躍.而作為核恐怖活動的潛在使用對象,乏燃料溯源研究也日趨增多.核恐怖活動涉及的裝置包括放射性擴散裝置、簡易核爆炸裝置和核爆炸裝置,其中放射性擴散裝置的風險最大[5].放射性擴散裝置可使用的放射性材料包括醫用放射源、工業用放射源、走私的核材料以及乏燃料等.其中乏燃料由于其強放射性一直受到高度關注,是制作放射性擴散裝置的一個重要選擇.與此同時,乏燃料的處置問題一直也是個熱點問題,且目前尚無合理的解決方案,無論是后處理還是放置貯存,都是有爭議的.目前乏燃料均處于放置貯存狀態,但隨著乏燃料數量的日趨增多,現有的貯存設施越來越難以滿足需求,這也就增大了乏燃料的擴散風險.雖然目前尚未出現乏燃料走私的案例(當然也有可能是發生了尚未被發現),但針對可能發生的場景進行相應的研究是非常必要的.而一旦截獲了乏燃料,通過α譜、β譜、γ譜以及各種質譜方法進行測量可以得到相應的核素信息,也即核取證技術中“表征”的主要工作,目前已經較為成熟.而對此進行的分析則屬于“解讀”工作的范疇,方法比較多元化,其中之一就是多元統計分析.多元統計分析在核取證溯源中的應用研究由于受到缺乏足夠實際測量數據的限制,因此在近些年才逐漸開展起來.此項研究的基本思路是：首先對各種堆型的乏燃料組分進行模擬,構建相應的數據庫;然后選取合適的核素用多元統計分析方法進行處理;最后對所得結果進行分析與評價.模擬的軟件通常包括ORIGENS,FISPIN等燃耗計算軟件[6],核素選取主要包括鈾钚同位素、穩定裂變產物或根據需求選取的裂變產物組等[7-14],數據處理方法包括因子分析、主成分分析、偏最小二乘法、線性判別分析等[15-27],但目前主要研究還是聚焦于方法的可行性分析.

本文主要聚焦于在核取證場景中的乏燃料鑒別方法研究,重點研究利用多元統計分析方法(包括因子分析、判別分析和回歸分析)進行乏燃料鑒別,以論證鑒別的可行性并對方法的適用性進行分析,為可能的乏燃料鑒別工作提供理論支撐.

2 理論與方法

多元統計分析是運用數理統計的方法來研究多變量問題的理論和方法,它可以對多個隨機變量間的統計規律進行研究,應用范圍較廣.多元統計分析具有包括簡化數據結構、分類與判別、變量間的相互關系以及多元數據的統計推斷等功能.在本文的研究中,希望利用因子分析、判別分析和回歸分析來實現數據的降維與可視化、未知乏燃料反應堆類型和初始裝料以及燃耗的判斷等功能.由于目前并沒有非常合適的公開的乏燃料數據庫,因此需要通過模擬計算來構建一個可供進一步研究的數據庫.在構建好數據庫后,分別利用因子分析、判別分析和回歸分析的方法對乏燃料的初始信息進行反演,并將結果相互比較,論證各方法的適用范圍,并以此形成較為合理的乏燃料鑒別方案.

2.1 因子分析

因子分析是多元統計分析方法中用于降維的一種方法.因子分析根據研究對象的不同可以分為R型和Q型因子分析.R型因子分析研究變量(指標)間的相互關系,通過對變量的相關陣或協方差陣內部結構的研究,找出控制所有變量的幾個公共因子(或稱主因子、潛因子),用以對變量或樣品進行分類;Q型因子分析研究樣品之間的相關關系,通過對樣品的相似矩陣內部結構的研究找出控制所有樣品的幾個重要因素(或稱主因子)[28].這里基于研究場景采用Q型因子分析.基本想法是,選定n個核素,通過數值模擬得到不同初始條件(堆型、初始裝料、燃耗)下乏燃料樣品中的這些核素的計算數據,并以此構建數據庫,這樣在數據庫中每個樣品的數據均為n維向量.然后尋找若干互不相關的n維向量,稱之為公共因子,并用這些公共因子的線性組合來表征初始的向量.這里舉個簡單的例子來進行具體的說明.例如選取9個鈾钚同位素(U-234,U-235,U-236,U-238,Pu-238,Pu-239,Pu-240,Pu-241,Pu-242)在乏燃料中的組分做研究,這樣每一個樣品提取出來的都是個9維向量.選擇4個樣品(A,B,C,D)進行分析,并利用三個公共因子(I,II,III)的線性組合來重新表征這4個樣品,即

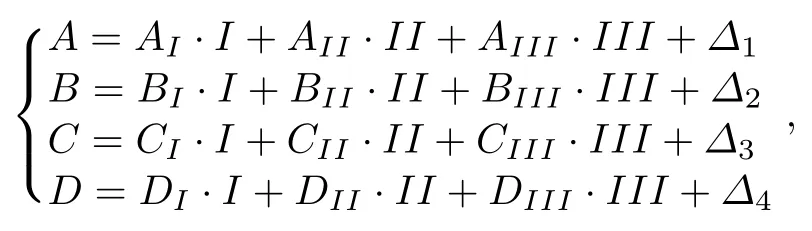
這里,AI,···,DIII等均為常數;Δ則是對于不同樣品的特殊因子,在滿足分析精度的要求時是可以省略掉的.這樣,之前的9維向量就可以投影到由I/II/III構成的新的三維空間的一個點上了,也就實現了將數據從9維降到3維的功能.

2.2 判別分析

判別分析是用于判斷樣品所屬類型的一種統計分析方法.判別分析問題通常可以這樣描述：設有k個m維總體G1,G2,···,Gk,其分布特征已知(如已知分布函數分別為F1(x),F2(x),···,Fk(x),或知道來自各個總體的訓練樣本),對給定的一個新樣品X,要判斷它來自哪個總體.根據判別函數的形式不同,判別分析可分為線性判別分析和非線性判別分析.對于本文研究情景而言,由于各組樣品的相互對立性較好,因此選取線性判別分析來進行研究.研究的基本思路是對已知的乏燃料數據按照堆型分組并計算各組的線性判別函數,然后將未知乏燃料數據代入進行分類判別.

2.3 回歸分析

回歸分析方法是多元統計分析的各種方法中應用最為廣泛的一種.它是處理多個變量之間相互依賴關系的一種數理統計方法.建立回歸分析的模型,就是將關心的問題具體化,考慮這些問題與哪些因素相關,然后用數據來估計因變量與自變量之間的關系.具體而言,就是將我們所關心的問題y表示成各個因素x的函數,即

y=f(x1,x2,···,xn).

如果將f(x) 具體化成線性形式,即這里u為誤差項,就得到了線性回歸模型.在本文的研究中,y可以是初始裝料或者是燃耗,而x則是乏燃料中我們所關心的核素的組分.

y=f(x1,x2,···,xn)=β0+β1x1+···+βnxn+u,

3 數據準備

本文的研究是基于乏燃料中的同位素組分,通過多元統計方法對乏燃料的來源信息(包括反應堆堆型、初始裝料以及燃耗等)進行鑒別.由于目前并沒有非常合適的公開的乏燃料數據庫,因此選擇利用程序MCORGS對不同的反應堆進行模擬[29,30],并選取各乏燃料樣品中的9種鈾钚同位素(U-234,U-235,U-236,U-238,Pu-238,Pu-239,Pu-240,Pu-241,Pu-242)組分構建數據庫.

根據反應堆堆型、初始裝料及燃耗的不同共選擇了148種不同的樣品,其中包括了初始裝料為UO2或者钚鈾氧化物混合(MOX)燃料的壓水堆(pressurized water weactor,PWR),初始裝料為天然鈾或者UO2的加拿大重水鈾反應堆(Canada deuterium uranium reactor,CANDU),初始裝料為MOX燃料的液態金屬快速增值反應堆(liquidmetal fast-breeder reactor,LMFBR),初始裝料為天然鈾的鎂諾克斯氣冷堆(MAGNOX),初始裝料為UO2的氣冷堆(gas-cooled reactor,GCR),以及初始裝料為高濃鈾的高溫氣冷堆(high temperature gas-cooled reactor,HTGR),具體參數見表1.這樣基于計算結果就可以構建相應的數據庫了.

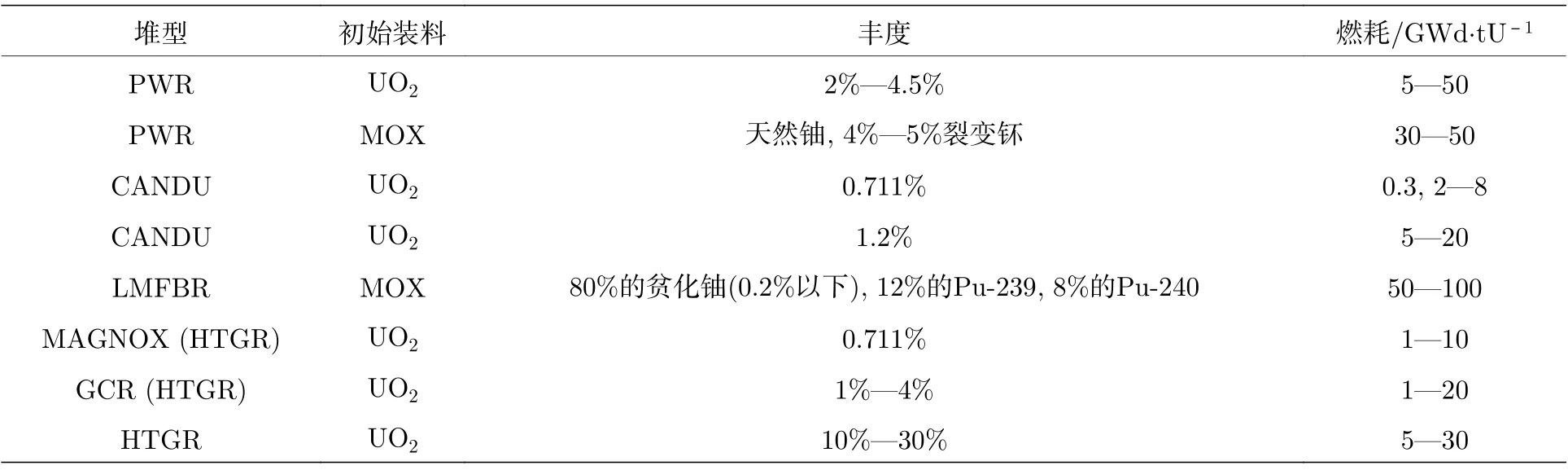
表1 反應堆模擬的輸入參數Table 1.Input parameters for reactor simulation.

此外,用同樣的方法選取了另外三個乏燃料樣品作為未知樣品(Uk1,Uk2,Uk3),其輸入參數如表2所列.

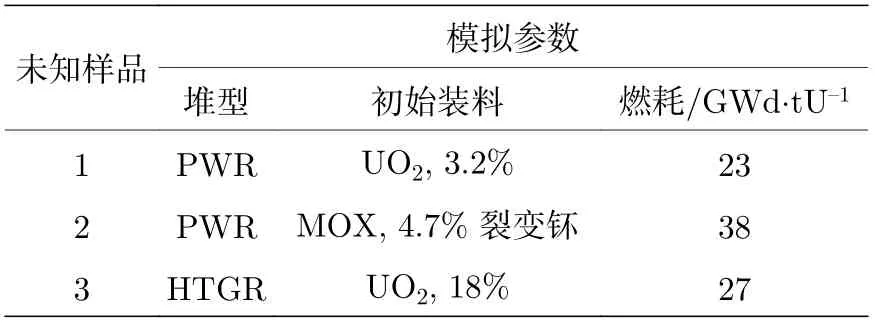
表2 未知乏燃料的輸入參數Table 2.Input parameters for unknown spent nuclear fuel.

4 結果分析

4.1 因子分析

4.1.1 降維與可視化

利用因子分析方法可以實現數據的降維與可視化.將數據庫中的每一個樣品都投影到三維空間上,即將每個樣品從9維降到3維,可以達到可視化的目的(見圖1)[31].

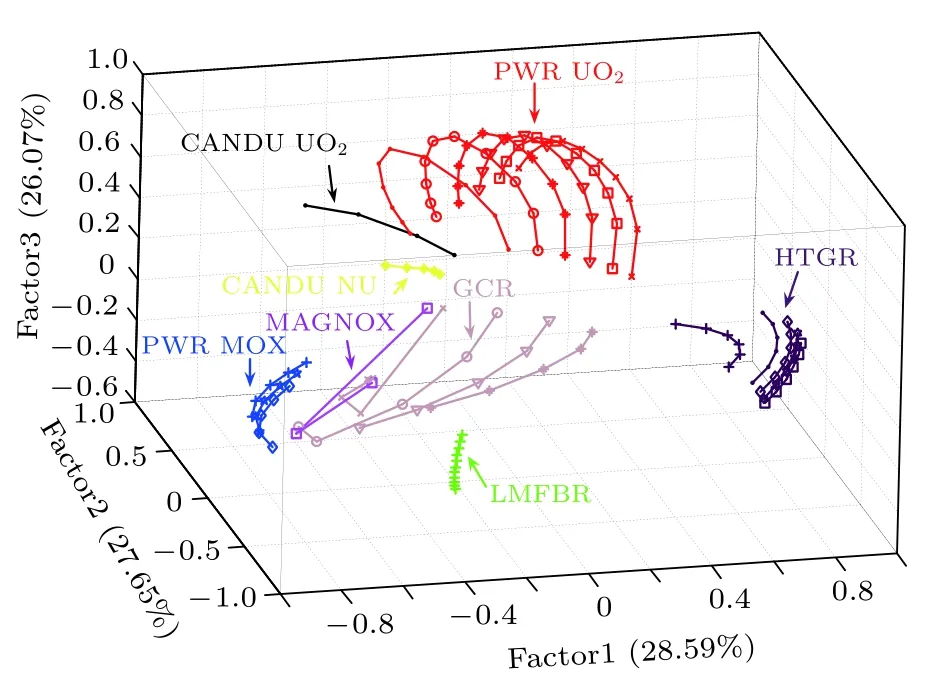
圖1 數據庫在3維空間的可視化處理Fig.1.Visualization of database in three-dimensional space.

圖1中的三個坐標軸就是前面提到的公共因子,在此例中均為9維向量.而不同顏色的點代表著來自不同反應堆的樣品(這里將反應堆類型及初始裝料類型都相同的視為同一來源),明顯地,不同來源的樣品在三維空間上形成了不同的組,并占據了不同的空間,也就是說因子分析方法可以用于區分反應堆類型.但這種區分能力是定性的,也就是說,在增加未知乏燃料樣品的數據后再進行因子分析,未知樣品在三維空間中落在哪個樣品堆里,就定性地判斷它們為同一堆型的.

4.1.2 初始裝料與燃耗的鑒別

通常來講,因子分析的作用在于降維與可視化處理以及分類工作,并沒有直接進行定量化鑒別的功能.也就是說,并不能直接通過因子分析方法鑒別出未知樣品的燃耗與初始裝料.但可以在因子分析結果的基礎上通過其他的方法近似預測一下未知樣品的燃耗與初始裝料,雖然這樣的精度并不一定非常好.

這里將三個未知樣品的乏燃料數據插入之前的數據庫中,然后通過已知樣品來預測未知樣品的燃耗與初始裝料.具體的方法是針對不同未知樣品選取合適的二維投影,并利用其周圍的四個點,通過海倫公式定量計算未知樣品的初始裝料與燃耗(如圖2所示).

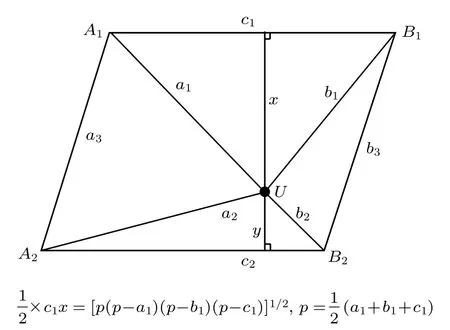
圖2 海倫公式示意圖(U點為未知樣品點,A1,A2,B1,B2為已知樣品點)Fig.2.Diagram for Heron’s formula (Ustands for unknown sample,A1,A2,B1,B2stand for known samples).

這里存在兩個假設,首先要假設平面上的數據變化是單調、線性的,此外還要近似認為未知樣品所落區域是平行四邊形.同時還要適當選取投影平面,不同的樣品需要的投影平面是不一樣的,因此通常誤差也是比較難以控制的,具體結果見表3.

不難看出,這種方法進行的定量鑒別還存在一定的誤差.值得注意的是,這是在三個投影平面的鑒別結果中的最優解,而在實際情況中,由于并不知道未知樣品的初始參數,因此并不一定會選取到最優解,這也就可能會進一步增加相對誤差.

4.2 判別分析

4.2.1 反應堆類型判斷結果

從因子分析的結果中不難發現,不同類型反應堆的乏燃料數據之間的差別還是很可觀的.因此將數據庫中的數據按照反應堆類型進行分類,其中PWR UO2和PWR MOX由于初始裝料本身存在很大的差異,因此看作兩種不同的反應堆.而后對數據庫中的數據進行線性判別分析,并將三個未知乏燃料的數值代入進行反應堆類型的判斷,結果如表4所列.

表3 因子分析鑒別結果Table 3.Result of identification by using factor analysis.

表4 反應堆類型判斷結果Table 4.Result for the determination of reactor type.

不難看出,利用線性判別分析對三個未知樣品反應堆類型的判斷所得到的結果都是正確的.其中未知樣品2和3的反應堆類型判斷是非常準確的,而未知樣品1的反應堆類型判斷稍有誤判概率.這是因為在本文的模擬中,PWR和CANDU堆所選取的反應堆模型是一樣的,再加上初始裝料類型相同,只有裝料量和燃耗上的區別,因此在進行反應堆類型的判斷時,會產生一些誤差,但并不影響判斷結果.而將線性判別分析的結果與因子分析的結果進行比較可以發現,因子分析對反應堆類型的判斷是定性的,也就是說是通過未知樣品落在降維后的空間中的位置來判斷其應該屬于哪一類型;而線性判別分析則可以更直觀地、定量地給出未知樣品屬于某一反應堆的概率,并選取最高概率確定其反應堆類型.因此相較于因子分析而言,線性判別分析更適合用于反應堆類型的判斷.

4.2.2 乏燃料初始裝料與燃耗的相關鑒別

根據前面對判別分析的描述不難看出,和因子分析一樣,判別分析并不適于進行定量化的鑒別,即當需要定量化地描述未知樣品的某一自變量,而這個自變量又并不完全和已知樣品的自變量相吻合的時候,判別分析是不適用的.

這里,基于線性判別分析,可以用以下的方法來近似計算初始裝料和燃耗.基本思路為：計算未知樣品對各個總體的線性判別函數值,對燃耗/初始裝料和各線性判別函數值進行多項式擬合,尋求極值點,并求出極值點對應的未知樣品的燃耗/初始裝料.這里應用到了距離判別的思想.利用馬氏距離來進行計算,其定義為[12]

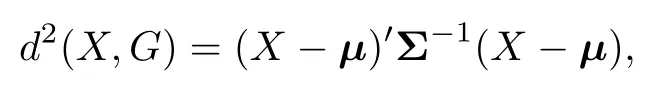
其中,G為考察的總體;X為未知樣品;μ為均值向量;∑為協方差陣.而線性判別函數值是與未知樣品和各總體的馬氏距離相關的,即

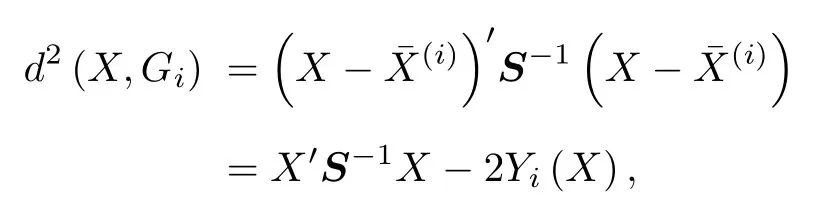
這里Gi是各數據組,為各數據組的均值,S為合并樣品協方差陣.也就是說,線性判別函數值越大,證明其馬氏距離越小,當線性判別函數取極大值時,馬氏距離為0,此時對應的燃耗/初始裝料值即為未知樣品的預測值.以未知樣品Uk1為例,將數據庫中的PWR UO2組的數據按照初始裝料繼續分組,然后通過線性判別分析來計算各組的線性判別函數,再將Uk1的數據代入到各線性判別函數中,擬合初始裝料-線性判別函數值(如圖3所示),尋求極大值點的初始裝料值,即認為是Uk1的初始裝料.

這里橫坐標為初始裝料值,縱坐標為線性判別函數值,擬合的結果為二次多項式,只要求極值處的橫坐標值即可.這樣按照該方法可以對三個未知樣品的初始裝料與燃耗進行鑒別.值得注意的是,對于不同的情形擬合出的多項式的階次是不一樣的,要根據擬合度進行判斷選擇.這樣得到線性判別分析結果與因子分析結果的比較,如表5所列.

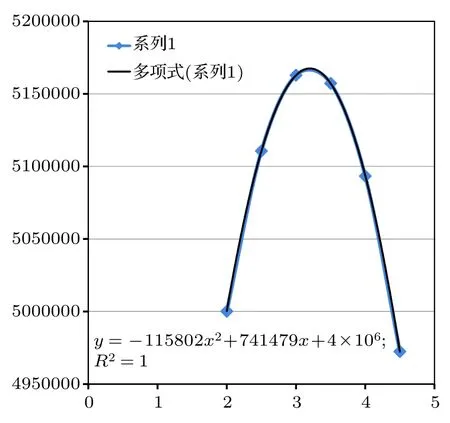
圖3 對未知樣品1的各線性函數值的多項式擬合Fig.3.The Polynomial fitting of the linear function values of unknown sample 1.

不難看出,線性分析的鑒別結果要普遍好于因子分析的鑒別結果.這里有幾點需要說明：首先,對于堆型的判斷,因子分析是定性的,而線性判別分析是定量的,因此雖然判斷的結果相同,但是還是線性判別分析要好一些;其次,對于初始裝料和燃耗的判斷,因子分析有很多假設和不確定性,線性判別分析則少很多.因子分析是3個投影平面選取最好的,這在現實應用中是不可能的,而線性判別分析則沒有這方面的要求.但仍需要注意到,對判別函數值擬合求極值的方法仍然會引入一些誤差.

4.3 線性回歸分析

通過之前的分析已經可以較好地分辨未知乏燃料的反應堆類型了,但是初始裝料和燃耗的相關反演還不盡如人意,因此這里采用線性回歸分析再次進行鑒別分析.對于三個未知樣品,選取其同反應堆類型的樣品數據重新構建數據庫,再利用線性回歸分析進行初始裝料與燃耗的鑒別分析,結果如表6所列.

不難看出,在初始裝料和燃耗的鑒別方面,線性回歸分析的結果要好于前兩種方法.這主要體現在兩方面：首先,線性回歸分析得到的結果更接近于真實結果,鑒別精度更高;其次,線性回歸分析的假設與限制更少,更具有普適性.同時,如果數據庫中自變量和因變量之間不是線性關系的話,回歸分析也能給出相對更為準確的鑒別結果.

5 三種多元統計方法比較

綜上所述,不同的多元統計方法針對的數據處理目的不同,可以實現的功能與適用范圍也就有所差別.簡言之,因子分析的主要作用是對數據進行降維,即簡化數據結構,使問題得到簡化而損失的信息又不太多.同時因子分析還具有初步的分類能力,但多偏于定性;判別分析的主要作用是對數據按照相似程度進行分類,且這種分類能力是定量的,相對于因子分析而言更為準確和實用.同時判別分析可以在一定條件下進行數值預測(在本文的場景里就是對未知樣品的初始裝料和燃耗進行預測);回歸分析則側重于對初始參數的預測,通過對已知樣品的乏燃料組分和初始參量進行回歸分析,來預測未知樣品的初始參量,因此在本文的場景中更適于進行未知樣品的初始裝料與燃耗的鑒別.具體的分析結果如圖4所示.

表5 線性判別分析與因子分析結果比較Table 5.The comparation of the results from discrimination analysis and factor analysis.

表6 利用線性回歸分析進行初始裝料與燃耗的鑒別分析的結果Table 6.Results for the determination of initial enrichment of uranium and burn-up by linear regression analysis.

圖4 三種多元統計方法的比較Fig.4.Comparation of the three multivariate analysis methods.

圖4中線性判別分析和線性回歸分析在數據簡化方面并不是不適用,而是其數據簡化過程并不像因子分析那樣可以直觀展示出來,二者的數據簡化過程都是為了后面的分類與鑒別做鋪墊的.從圖4不難看出,乏燃料的鑒別過程是首先通過因子分析進行數據簡化,通過可視化初步展示鑒別的可行性,然后通過判別分析進行未知乏燃料反應堆堆型的判斷,最后再用回歸分析來確定未知乏燃料的初始裝料和燃耗.這是一個串行過程,例如在進行完反應堆堆型的判斷后,會對數據庫進行一次縮減,將堆型不符合的數據舍棄,然后用剩下的數據再進行下一步分析.與此同時,因子分析在此過程中并不是必需的,可視情況決定此步驟是否進行.

6 結 論

本文對利用多元統計分析方法進行乏燃料鑒別開展了研究,主要應用了因子分析、線性判別分析以及線性回歸分析的方法.通過研究發現,利用不同的多元統計方法可以實現不同的功能,通過這些方法的有機組合,可以形成一個比較完整的乏燃料鑒別方案.這樣基本理清了乏燃料鑒別的流程框架,即利用不同的多元統計方法對乏燃料的不同來源信息依次進行鑒別,并根據鑒別結果精簡數據庫,然后進行下一步鑒別.研究表明,多元統計分析方法可以通過已知的乏燃料數據庫來進行未知乏燃料鑒別,隨著各國以及國際核取證數據庫的不斷發展以及核取證研究與應用的不斷推進,多元統計分析方法在未來核取證溯源工作中可以發揮相應的作用.