一種基于卷積神經網絡的信號調制方式識別方法

桂祥勝，洪居亭，代華建，孫田亮

（四川大學電子信息學院，成都 610065）

1 背景介紹

在通信信號處理領域，特別是在非協作通信信號盲解調研究領域，每時隙突發信號的調制方式不同，必須進行信號的調制方式自動識別。信號的調制方式識別效果會影響整個盲解調系統。傳統的專家系統已經被研究多年，然而依然存在準確性低、效率低等問題。近年來，深度學習方法廣泛應用于圖像處理[1-2]和語音識別[3-4]領域，取得了不錯的效果。信號星座圖是表征數字調制信號的一種重要方式，它能夠直觀地將信號以圖片幾何特征的形式展示出來，便于人們觀察和分析。傳統的人眼分辨方法依賴于一定的專業知識、耗時且識別準確率較低。我們將深度學習方法引用到通信信號處理領域，提出了一種基于卷積神經網絡的信號調制方式自動識別方法。

2 生成數據集

2.1 原始數據的生成

實驗需要獲取多種調制方式、寬信噪比范圍、帶有標簽的數據，這在短時間內難以通過采集真實信號來實現。本次實驗所需數據通過仿真產生，實驗選取部分數據進行訓練學習，使用另外的數據進行驗證測試。仿真生成數據過程主要有生成隨機0-M 數字（M為調制階數）、MQAM/MPSK 調制、成形濾波、載波上變頻、信道仿真（加性高斯白噪聲信道）、IQ 正交解調、匹配濾波、重構信號星座圖并保存。整個生成數據流程如下所示。

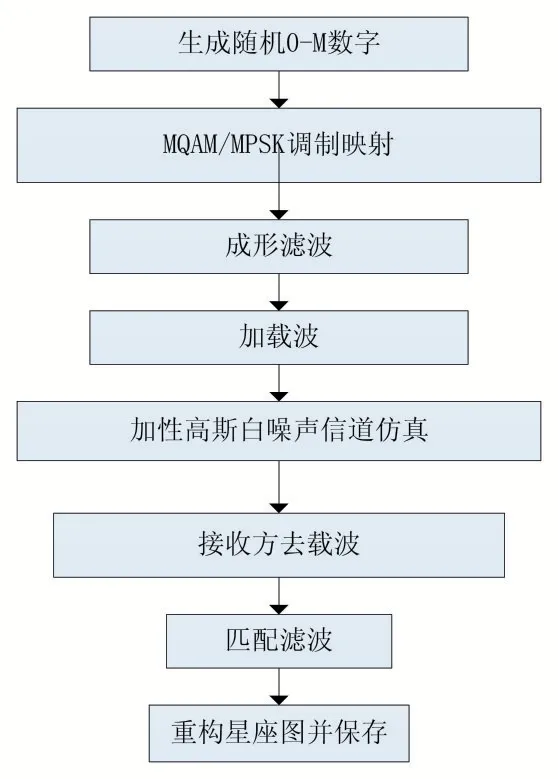
圖1 生成信號流程圖

本次仿真共生成 7 種調制方式（BPSK、QPSK、8PSK、QAM8、QAM16、QAM32、QAM64）信號，每種調制方式信號信噪比為-20dB、-18dB、…、+16dB、+18dB。每種調制方式在某一信噪比下共有1000 條數據，生成1000 張星座圖片，每張圖片包含1000 符號信息（即每張星座圖圖上有1000 個點）。仿真生成的基帶信號經成形濾波后時域圖形如下所示。

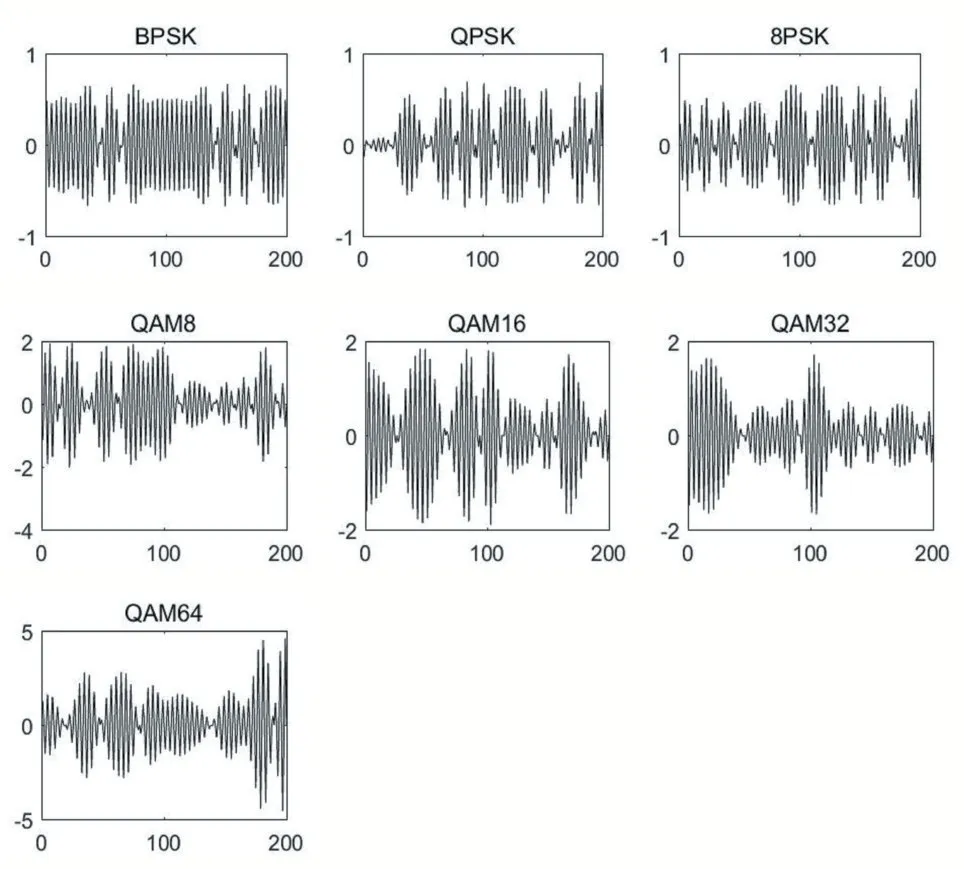
圖2 經成形濾波后的信號時域圖

2.2 IIQQ正交解調和星座圖

在通信系統接收方通常需要將接收到的中頻信號變成基帶信號這就需要數字下變頻操作。數字下變頻（DDC）通常包括IQ 正交解調和低通濾波兩部分。IQ 正交解調需要知道信號的載波頻率，低通濾波器截止頻率的設置和信號帶寬相關。經過低通濾波過后即可得到IQ 兩路信號，此時得到的IQ 路信號還需要經過匹配濾波、下采樣符號同步等過程，才能重構信號星座圖。

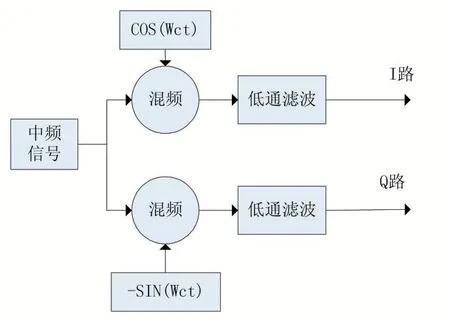
圖3 數字下變頻原理說明圖

圖4 IQ兩路信號和幅度相位關系說明圖

IQ 信號能夠同時包含信號的幅度和相位等信息，IQ信號可以輕松地形成一個復信號。大多數數字調制將數據映射到IQ 平面中的許多離散點，稱之為星座圖[5]。

3 基于CNN的調制方式識別工作原理

3.1 卷積網絡結構

基于CNN 的調制方式識別模型網絡框圖如下所示。輸入層輸入的是150×120 像素尺寸大小的信號星座圖，經過3 個卷積層、3 個池化層，扁平層，到最后按照7 種調制類型輸出。訓練集數據都是帶有標簽的，即事先知道某信號的調制方式，不斷學習圖片對應調制類型，整個系統通過梯度反向傳播機制，不斷調節其中的相關參數，使整個系統的輸出結果和標簽結果的誤差最小。這就是整個模型系統的一個學習過程。

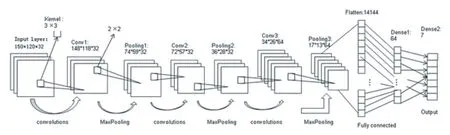
圖5 CNN網絡模型結構圖

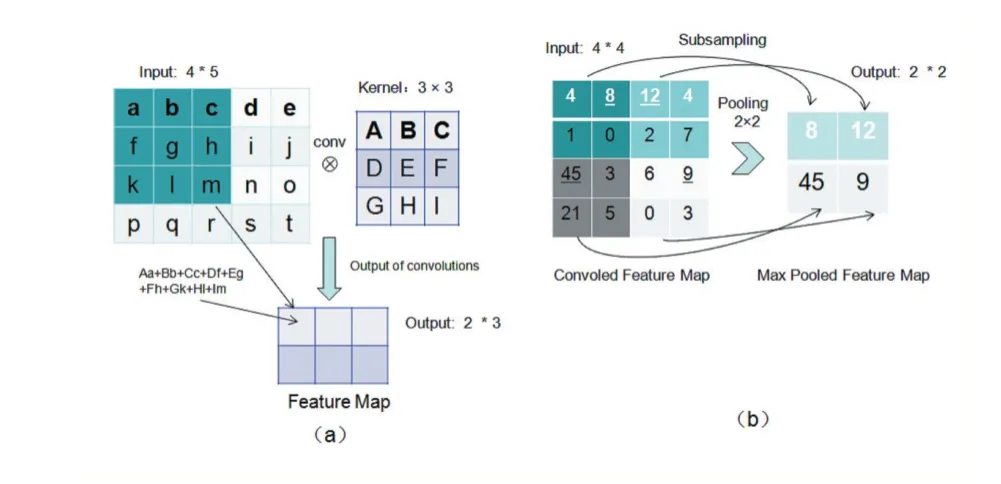
圖6 卷積操作池化說明圖

卷積池化操作是CNN 中重要的組成部分，上圖左圖中假設了4×5 大小的輸入矩陣數據，和3×3 的卷積核進行卷積運算的過程，得到信號的特征圖。上圖右圖是4×4 的特征層進行2×2 最大池化的運算過程。

CNN 的功能是從特定模型中提取特征，然后根據特征進行分類識別、預測或做出決策。在此過程中，最重要的一步是特征提取，即如何提取能夠最好地區分事物的特征。如果提取的特征不能進行分類，那么特征提取步驟將毫無意義。網絡模型中卷積層層數越多，更容易把握輸入信號的細微特征[6]。然而，在深度神經網絡的設計中，應該在每個階段考慮卷積層數和核大小，嘗試以最少的計算量獲得最佳結果，網絡設計需要平衡網絡結構的寬度和深度。

對于相同的CNN 網絡結構，迭代的次數，數據量的大小和學習率都會影響模型的分類結果和有效性。這些參數的設置都需要在實踐中不斷嘗試、不斷分析修改。在本實驗中，設計的CNN 模型使用3 層卷積網絡層，卷積核大小為3×3，迭代次數為40，隨著訓練量的變化調整參數大小。

3.2 每層輸入和輸出大小

輸入層：150×120 像素大小的信號星座圖。卷積層1（Conv1）：由 3×3 內核生成的 148×118 個特征圖。池化層第 1 層（Pooling1）：從 2×2 區域進行二次采樣后的74×59 個像素圖。卷積層 2（Conv2）：由 3×3 內核生成的 72×57 個特征映射。池化層第 2 層（Pooling2）：從 2×2 區域進行二次采樣后的36×28 個特征映射。卷積層3（Conv3）：由 3×3 內核生成的 34×26 個特征映射。池化第 3 層（Pooling3）：從 2×2 區域進行二次采樣后的17×13 個特征映射。完全連接層（F1atten）：從 Pooling 3的所有像素轉換的 14144 個節點，即 17×13×64=14144。Dense1：64，Dense2（輸出層 Output）7 個結點，Softmax 分類器分類輸出，輸出7 個節點，代表七種不同的調制方法。

3.3 星座圖

由于卷積和池化操作，CNN 可以從圖像細微差別中檢測到信號特征，來分類識別信號。我們使用七種最常用的調制方法（BPSK，QPSK，8PSK,QAM8,QAM16，QAM32，QAM64）作為例子來說明。從下圖可以看出，BPSK 信號星座圖分布在x=0 軸兩端，成2 個塊團狀；QPSK 信號分布X 軸Y 軸正負兩側。呈現4 個團塊狀；8PSK 分布成8 個塊團，且每個塊團離坐標原點的距離相等，8 個塊團形成了一個圓。QAM16 均勻分布在坐標軸四個象限，每個現象有四個團塊，共16 個團塊。綜上所述，不同數字調制信號星座圖的幾何形狀不同，在實際工程中，通信工程師經常會根據星座圖形狀來判斷信號的調制方式。

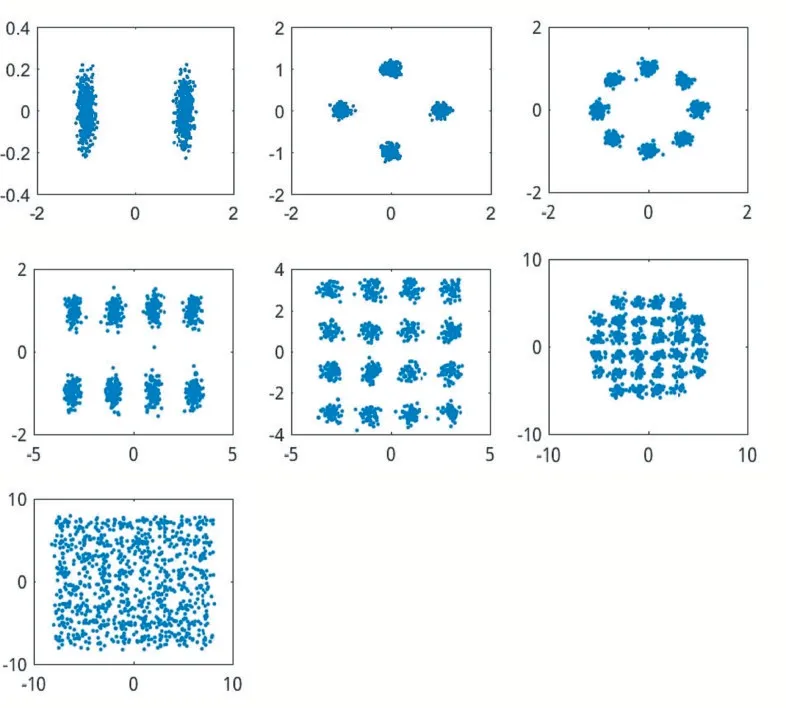
圖7 在SNR為10dB時BPSK、QPAK、8PSK、QAM8、QAM16、QAM64調制信號的星座圖

4 實驗和結果

4.1 機器學習模型的選擇

實驗時選擇了通信系統中常用的七種調制方式，并在不同數量的訓練集下進行訓練分類識別測試。基于其他研究人員以前的工作，知道卷積神經網絡具有計算復雜度低和識別準確率高的優點[7-8]。特別是在圖像處理領域，卷積神經網絡更是具有其他模型結構不可替代的效果，實驗中選擇卷積神經網絡模型來訓練星座圖。

4.2 圖片尺寸

當執行CNN 圖像分類時，不可避免地要考慮模型輸入圖像的大小，圖像越大，模型計算量就越大，分類識別也就越耗時；圖像太小又會看不清圖像幾何輪廓，影響模型判斷識別。經過多次反復嘗試，最終確定輸入的星座圖像大小為150×120 像素。

4.3 圖片類型

為了得到最佳分類識別效果，選擇信號不同的特征圖，分別進行實驗。選擇相同的信號，分別生成相同圖像大小的時域頻域星座圖形，利用相同的模型進行訓練測試，信噪比為8 時的識別效果如下表1 所示。從表1 可以看出，星座圖具有更好的特征表現效果。

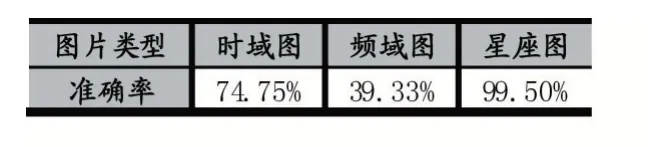
表1 當SNR 為8dB 時，不同的特征圖像分類識別精度

在某一信噪比下，訓練集中包含了7 種調制方式信號星座圖，每種調制方式400 張圖片，共2800 張星座圖片。驗證集數量和訓練集一樣，總共也是2800 張圖片。測試集包含7 種調制方式信星座圖，每種信號200 張圖片，總共有1400 張圖片。部分信噪比下，模型的訓練表現如圖8 所示。

圖8 不同信噪比下的訓練表現

如圖8 所示，不同信噪比下的信號隨著訓練迭代次數的增加，模型的損失值越來越小，模型驗證的準確率越來越高。信號信噪比較低時，損失函數起始瞬時值較大，損失值下降較慢。在-20dB 和-6dB 時，信號起始損失值均大于1.5。信噪比較低時，模型的驗證準確率也較低，比如在-20dB 是，模型的準確率在76%左右。

4.4 驗證結果

在每個SNR 下，選擇七種調制方式共1400 張圖片輸入到已經訓練的模型網絡中進行分類識別，實驗結果如圖9。

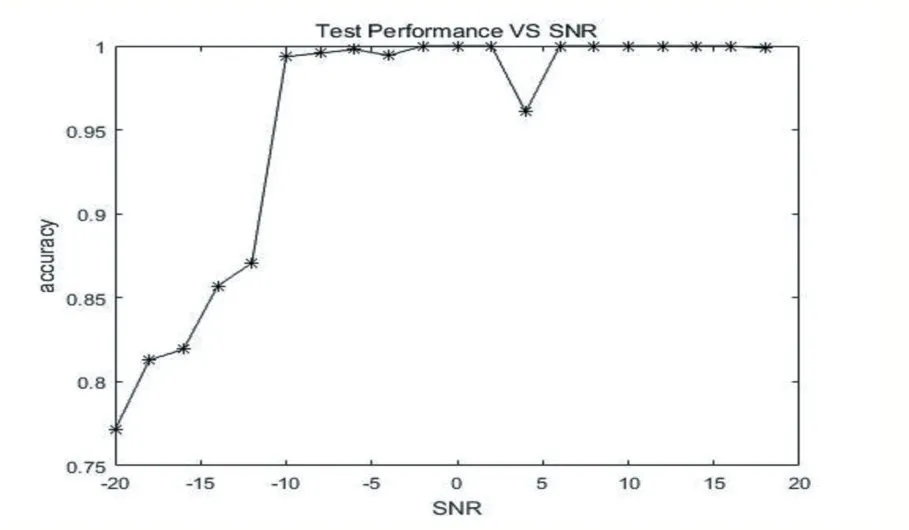
圖9 不同信噪比下的測試表現

從實驗結果來看，利用星座圖特征，基于卷積神經網絡的識別模型識別準確率高。在-20dB 下，識別效果得到77%，-10dB 及以上，模型的分類識別準確率趨近100%。分類效果遠優于傳統分類方法。

5 結語

在圖像分類領域，CNN 訓練模型具有其他機器學習方法所不具備的優點。通信信號星座圖蘊藏著調制特征信息，卷積神經網絡具有較強的特征學習能力，利用卷積神經網絡模型能夠很好的實現調制分類識別。本文提出的一種基于CNN 的信號調制方式識別方法，選用七種常用的數字調制信號進行實驗，結果表明該方法能夠高效準確實現信號調制方式自動識別。與其他調制分類方法相比，CNN 使用少量數據集圖片，花費較少的訓練時間，即可獲得理想的分類結果。對于信噪比大于-10dB 的信號，模型分類準確率接近100%。結果表明，本文提出的分類識別方法切實有效。同時，它還為我們提供了一種新的思維方式，當一維數據信號進行實驗效果不佳時，我們可以考慮換種思路，例如增加特征的維度，將一維數據轉換成二維圖像，可以從二維圖像方面著手開始解決問題，可能效果會變得更好。

6 未來工作

實驗結果比傳統專家系統產生了更好的結果，但對于新興的機器學習領域（深度學習），信號處理缺乏大量真實有效帶標簽的數據。本文在實驗中使用的數據采用仿真產生，與實際接收的通信信號數據之間存在差異，特別是實際信號中的頻偏、相偏、多徑干擾等，都會對實驗結果產生影響。僅依靠機器學習（深度學習）本身并不是有效的解決方案，期待能夠在不久的將來結合機器學習方法與信號處理方法，在通信信號處理領域取得突破。雖然我們也在努力優化CNN 的網絡結構，不斷調整模型參數，但仍然有很大的空間來優化模型，以期達到最佳的分類結果。例如卷積層的層數增加，卷積核的大小變化，迭代次數修改等。當然，在實驗中將訓練數據集從一維數據轉換為二維圖像是一種處理思想上的突破。研究人員[9]已經在時域和頻域進行了語音信號分析，無論數據信號是否可以轉換到其他域進行訓練分析，或者轉換為多維域進行測試和分析，還有很多工作需要去做。