直方圖受限的窄動態范圍彩色圖像細節增強

王海峰 章 怡 杜卓明

1(江蘇理工學院信息中心 江蘇 常州 213001)2(江蘇理工學院計算機工程學院 江蘇 常州 213001)

0 引 言

一些圖像(如水下圖像、遙感圖像和紅外圖像等)在采集時，由于受到天氣環境、場景、光照不均勻等因素的制約，使得得到的彩色圖像動態范圍比較窄、對比度偏小，顯得局部細節不突出，層次感差等缺陷，從而無法滿足實際應用[1-3]。因此，常常需要對彩色圖像進行增強處理，主要是為了方便后續圖像處理與分析(如邊緣提取、模式與識別等)和顯示設備對視覺效果的改善。相對于灰度圖像，彩色圖像包含的信息更豐富，對后續圖像分析更有優勢[4-6]。

在已提出的各種圖像增強技術中，基于全局直方圖均衡(GHE)的圖像增強技術由于其簡單性和有效性而備受關注[7]。雖然GHE應用較為廣泛，但是它仍然存在三種缺陷：過增強、不期望的偽影和細節信息容易丟失，于是，人們又提出了各種基于HE的圖像增強技術來克服這些缺點[8]。Kim通過灰度均值將原始直方圖分割成兩個子直方圖，提出一種亮度保持的雙直方圖均衡BBHE算法(Brightness preserving bi-histogram equalization)[9]。然后，Wang等用灰度中值代替均值，提出了二元子圖像直方圖均衡DSIHE(Dualistic sub-image histogram equalization)[10]。基于BBHE思想，研究者們又提出了許多類似的算法，如最小平均亮度誤差雙邊直方圖均衡MMBEBHE(Minimum mean brightness error bi-HE)[11]、遞歸均值分割的直方圖均衡RMSHE(Recursive mean-separate HE)[12]和修改直方圖的雙邊均衡BHEMHB(Bi-histogram Equalization using Modified Histogram Bins)等[13]。除了上述直方圖分割方法，還提出了諸如對比度受限的自適應直方圖均衡CLAHE(Contrast limited adaptive histogram equalization)[14]與平臺受限的雙邊直方圖均衡BHEPL(Bi-histogram Equalization with a Plateau Limit)等直方圖剪切方法[15]。

上述直方圖均衡的相關方法可以改善正常范圍[0,255]的彩色圖像視覺效果，但對動態范圍比較窄的圖像，如低照度的水下圖像(動態范圍處于低段)、低對比度“蒙紗”圖像(動態范圍處于中段)、曝光過度(動態范圍處于高段)等容易出現過增強，增強的圖像視覺效果不明顯[16]。因此，本文提出了一種直方圖受限的窄動態范圍的彩色圖像增強，在RGB空間直接對三分量進行直方圖受限的增強。算法主要分為3個階段：首先，算法設定累積概率密度閾值CT，計算對應的直方圖閾值HD，并通過直方圖閾值HD將輸入圖像直方圖分割成兩個子直方圖H1和H2；其次，對大于直方圖閾值的子直方圖H1，在[A,B]范圍內進行等間隔分布，進而得到等間隔分布的直方圖H1-1；最后，對小于直方圖閾值的子直方圖H2進行非線性映射至H1-1，從而得到增強的圖像。與現有的幾種基于直方圖的圖像增強算法相比，該算法不僅在視覺效果和圖像質量評估指標上都取得了很好的性能，而且為研究人員如何控制增強圖像的對比度提供了另一種途徑。

1 算法設計

1.1 設計原理

RGB色彩就是常說的三原色，R代表Red(紅色)，G代表Green(綠色)，B代表Blue(藍色)。自然界中肉眼所能看到的任何色彩都可以由這三種色彩混合疊加而成，因此也稱為加色模式。在日常生活中，圖像顯示設備如電視機、計算機顯示屏、智能手機屏幕等都采用RGB模式。因此算法設計直接在RGB模式中處理，無需轉換顏色模型，算法設計框圖如圖1所示。

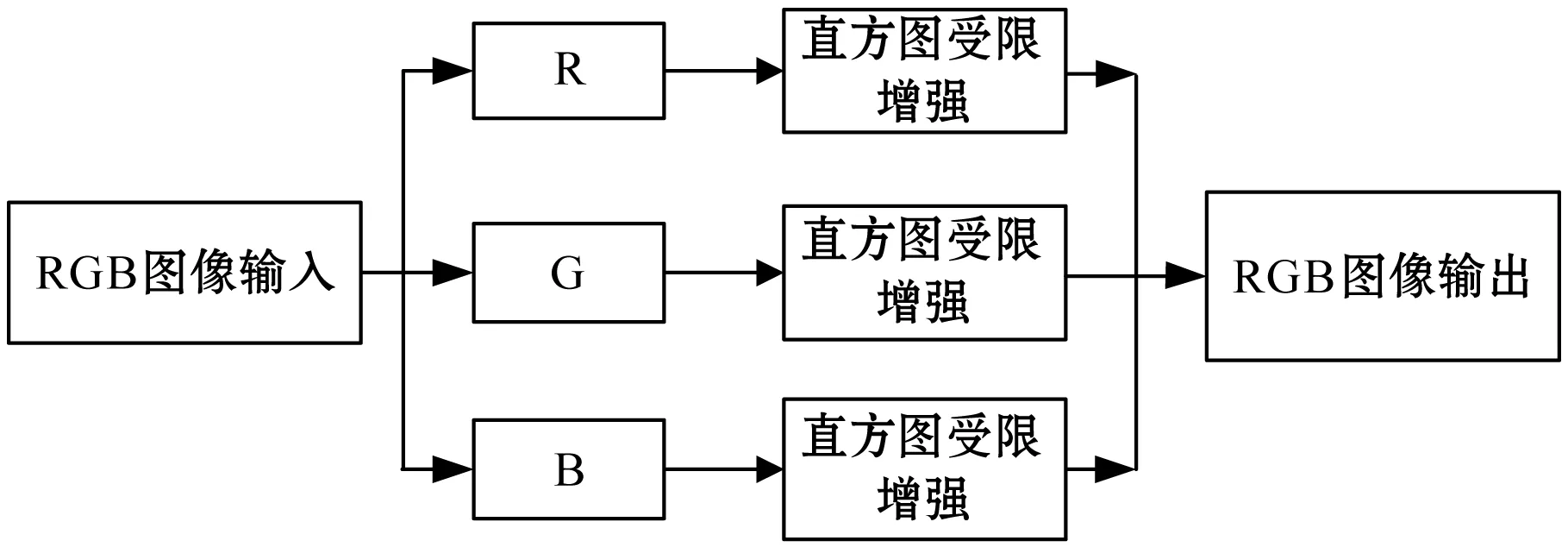
圖1 算法設計框圖

1.2 直方圖受限的對比度增強

一幅M×N灰度圖像I的直方圖、灰度概率密度函數、累積概率密度函數[17-19]分別定義為:

H(i)=nii=0,1,…,S-1

(1)

(2)

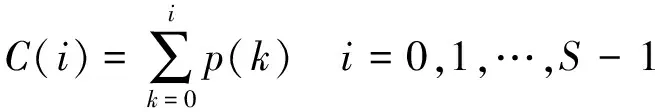
(3)

式中：i為灰度值，S為最大灰度級，8位灰度圖S=256。

使用最廣泛的對比度增強方法是基于直方圖均衡化的相關算法，這些算法在處理圖像時經常會出現偽影及信息量的丟失。因此，我們希望能夠找到一種方法，在改善不同場景圖像(如動態范圍比較窄的低對比度圖像)對比度的同時，能夠減少視覺偽影，提高輸出圖像中的信息含量，使得增強的圖像達到最佳視覺效果。算法主要分為直方圖分割、直方圖調整和直方圖映射三部分。

算法的初始階段是對輸入圖像直方圖的分割。設原始直方圖的累積概率分布閾值為CT，由式(1)和式(2)計算對應的直方圖閾值HD,通過該直方圖閾值HD將輸入圖像直方圖分別分割成H1和H2兩個子直方圖，H2稱為受限制的直方圖，分割示意圖如圖2所示，分割表達式如下：

(4)

(a) 原始直方圖

(b) 分割后的直方圖H1

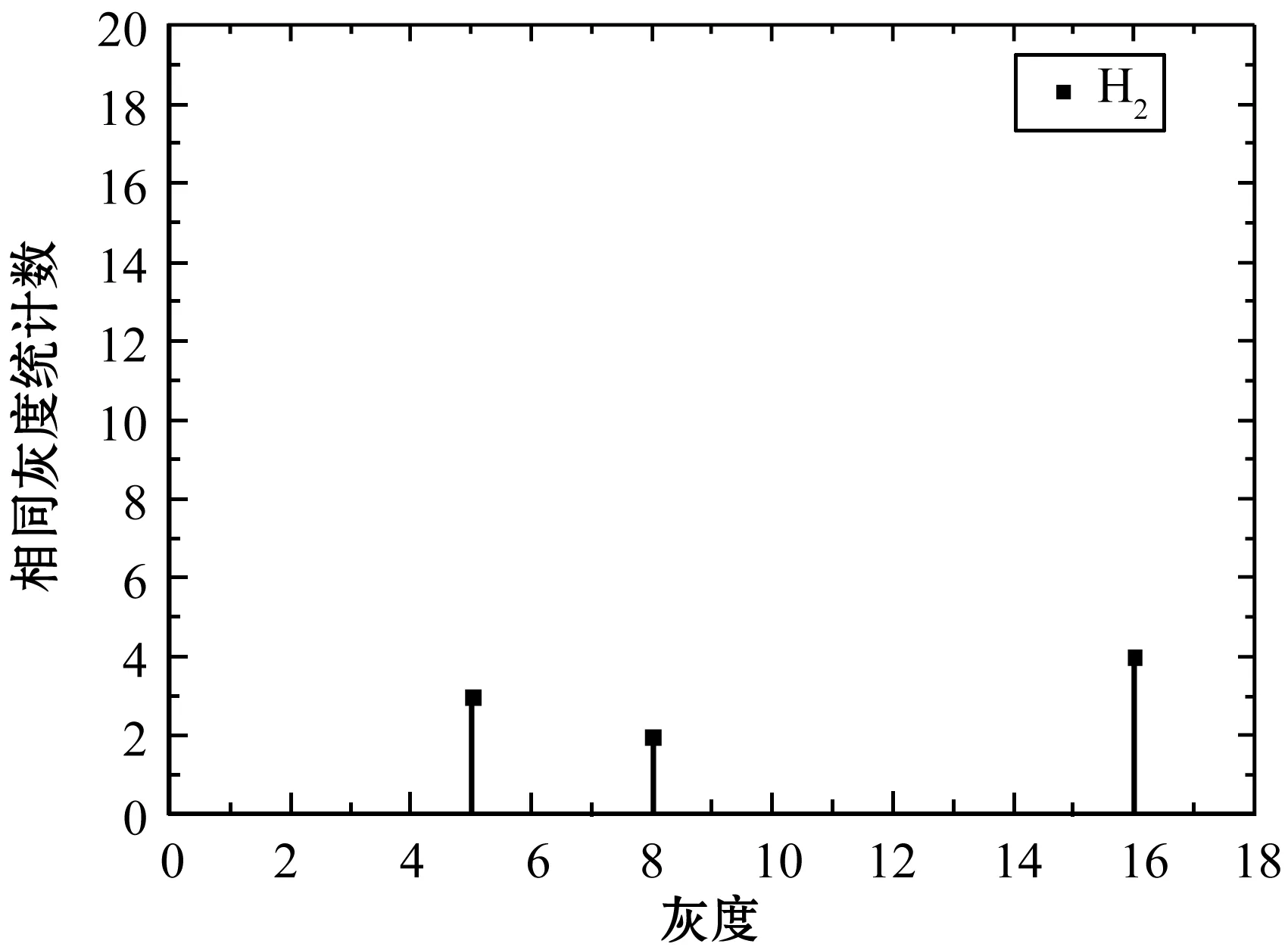
(c) 分割后的直方圖H2圖2 直方圖分割示意圖

算法的第二階段是對子直方圖H1做等間隔分布。設灰度值范圍為[a,b]，讓子直方圖H1在此灰度范圍等間隔分布，等間隔分布后的直方圖記為H1-1，直方圖等間隔分布定義為：

(5)

式中：y為子直方圖H1-1對應的新灰度值，m是子直方圖H1不等于0的個數，j是個數變量； 8位灰度圖像中a=0，b=255；round()為取整函數。

算法的最后階段是將受限子直方圖H2映射至子直方圖H1-1中。設i是子直方圖H1的索引灰度值變量，q是受限子直方圖H2的索引灰度值，映射的原則是：(1) 依次從受限子直方圖H2中取出一直方圖(該直方圖所處位置的索引灰度值是q)，將索引灰度值q逐個與i值比較，選出最接近索引灰度值q的i值(即it)，數學表達式為式(6)；(2) 確定it在子直方圖H1的位置t(即it對應的直方圖處于第t個)；(3) 最后，在子直方圖H1-1中，找到第t個直方圖對應的新索引灰度值yt(yt即為灰度值q需要映射后的新灰度值), 計算公式如式(7)，映射過程示意圖如圖3。

(6)

(7)

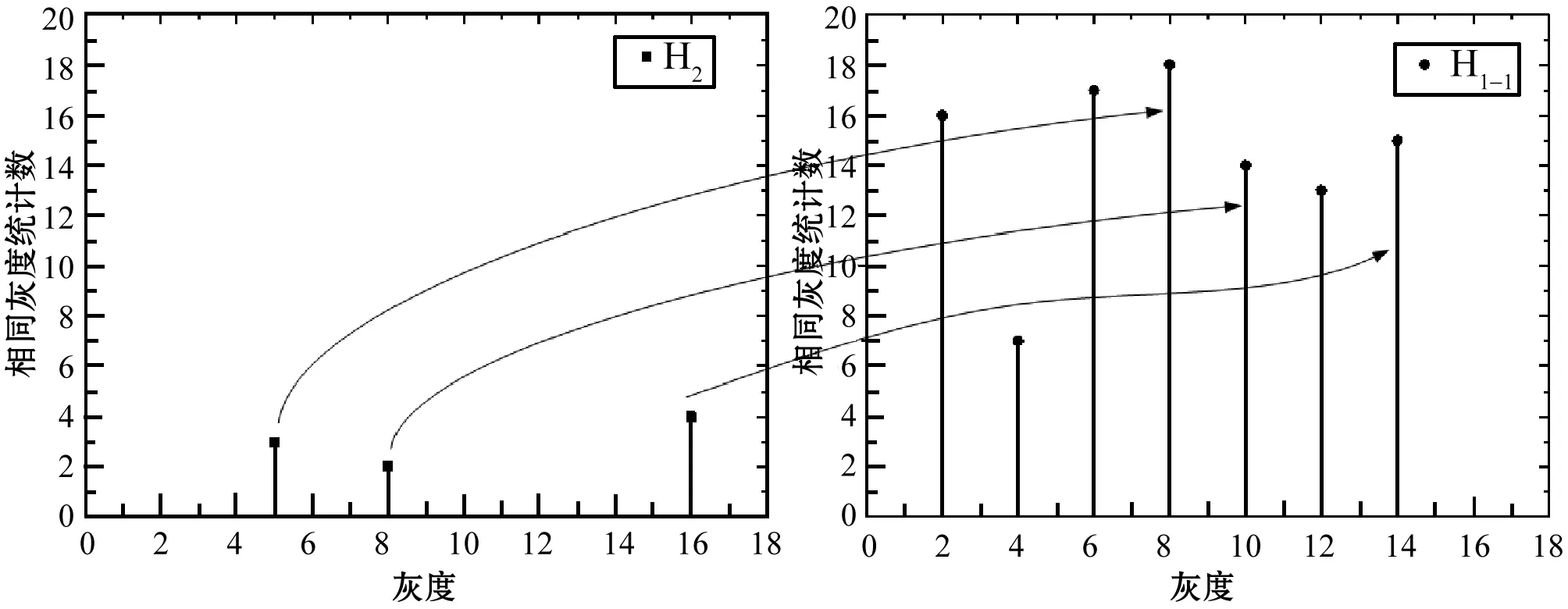
圖3 受限直方圖的映射過程示意圖

2 實驗結果與分析

本文實驗圖像小部分來自互聯網，大部分為相機拍攝，網絡圖片未用于商業目的，主要用于算法測試。實驗環境：Windows7系統Intel Pentinum CPU G860，主頻3.0 GHz，內存4 GB，算法語言MATLAB 2016b。

2.1 對比度可控性

為保證增強圖像不失真，參數CT的取值范圍一般為[0.9，1]，CT值越小，輸出圖像的對比度越大，反之對比度則越小。實驗中用圖像的標準差衡量對比度指標，標準差越大，說明圖像明暗對比大，即圖像對比度則大，反之則相反。圖4是對100幅彩色圖像進行測試對比度可控性，計算增強圖像的標準差均值隨參數CT變化情況：a=0、b=255，參數CT在[0.9，1]變化。

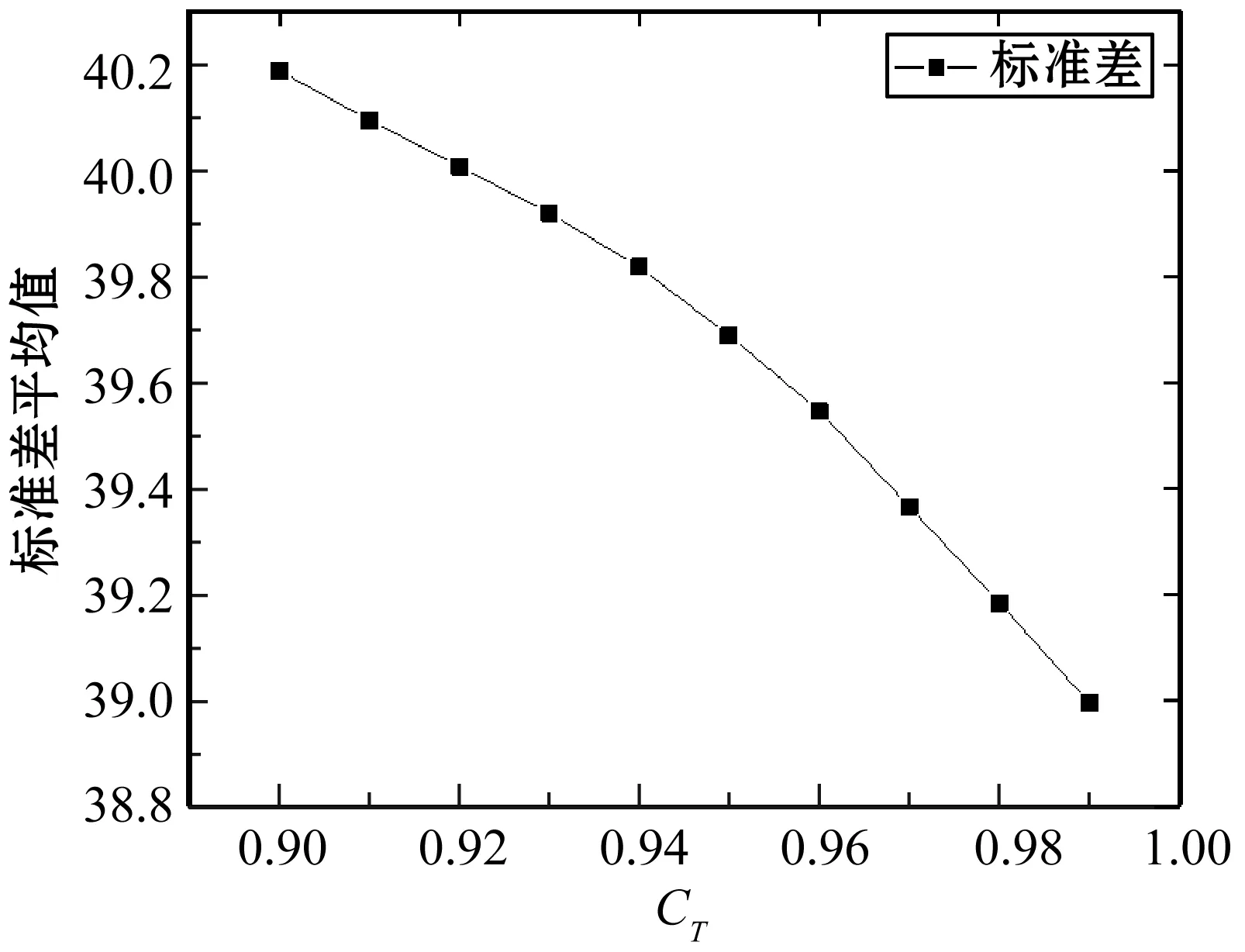
圖4 對比度可控性測試圖

2.2 算法比較

為檢驗算法處理不同動態范圍圖像的有效性，實驗選取了3幅窄動態范圍在低段(夜間圖像)、中段(水下圖像)和高段(大霧圖像)圖像，以及1幅全動態范圍[0，255]的紅外圖像，動態范圍如對應直方圖所示。與本文算法相比較的算法為BBHE、MMBEBHE、BHEMHE、DSIHE、RMSHE與BHEPL6種算法，并采用標準差、信息熵和峰值信噪比3項客觀指標評價實驗結果，結果表中最大數值用粗斜體加以突出。

(1) 實驗1：窄動態范圍處于低段的夜間圖像如圖5所示。

(a)原圖(b) BBHE

(c) MMBEBHE(d) BHEMHE

(e) DSIHE(f) RMSHE

(g) BHEPL(h) 本文

(a′) 原圖(b′) BBHE

(c′) MMBEBHE(d′) BHEMHE

(e′) DSIHE(f′) RMSHE

(g′) BHEPL(h′) 本文圖5 增強效果與直方圖

表1標準差數據顯示7種算法都圖像都進行了增強，其中增強效果比較明顯的為DSIHE(70.17)、BBHE(63.56)和本文算法(59.35)，其余算法則稍弱，這與人的視覺感覺一致。從暗區域細節的視覺效果來看，本文算法增強圖像的暗區域細節比其他任何一種算法處理得更清晰。表1中信息熵最大數值是本文算法(7.46)，進一步表明本文算法增強的圖像細節信息與其他算法相比最豐富。

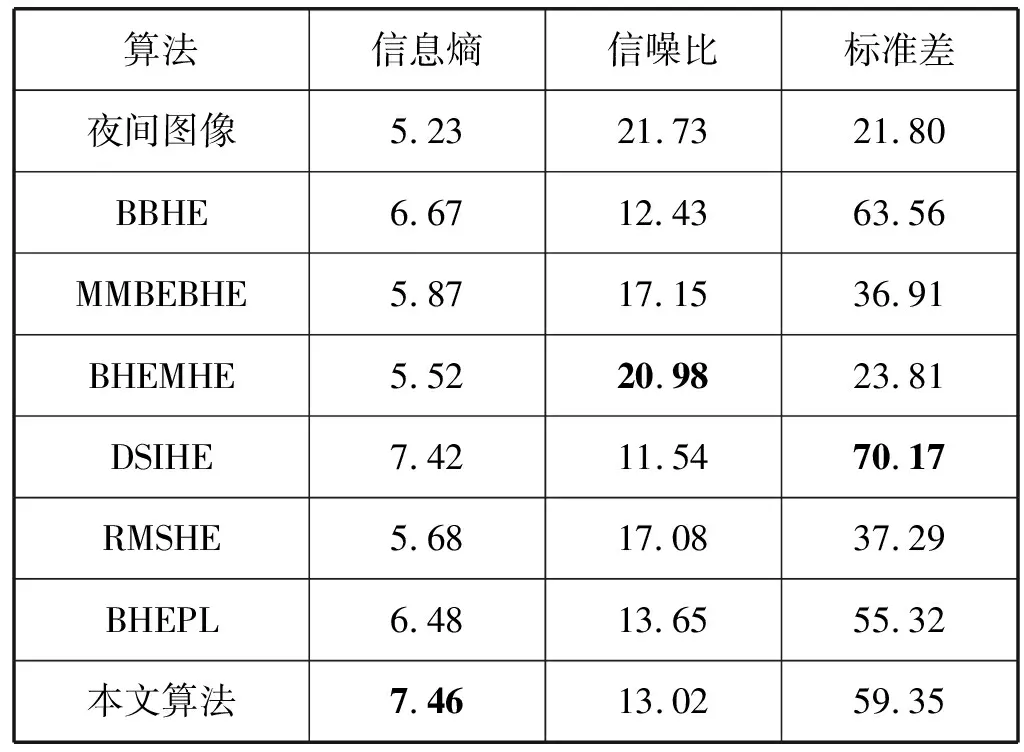
表1 實驗1結果數據

(2) 實驗2：窄動態范圍處于中段的水下圖像如圖6所示。

(a) 原圖(b) BBHE

(c) MMBEBHE(d) BHEMHE

(e) DSIHE(f) RMSHE

(g) BHEPL(h) 本文

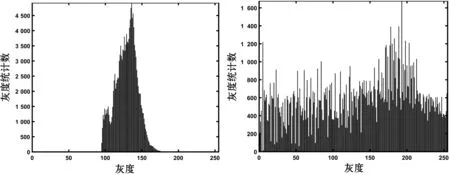
(a′) 原圖(b′) BBHE

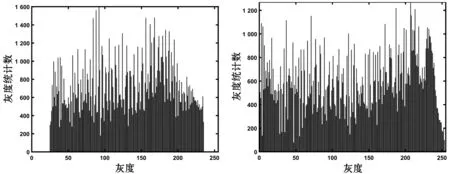
(c′) MMBEBHE(d′) BHEMHE

(e′) DSIHE(f′) RMSHE

(g′) BHEPL(h′) 本文圖6 增強效果與直方圖

從圖6各種算法對水下圖像增強的視覺效果看，7種算法中，本文算法和BBHE算法增強的效果較好，其他算法增強效果稍差些。表2中本文算法信息熵值最大為7.77，說明本文算法增強的圖像細節信息最多。

表2 實驗2結果數據

(3) 實驗3：窄動態范圍處于高段的大霧圖像如圖7所示。

(c) MMBEBHE(d) BHEMHE

(e) DSIHE(f) RMSHE

(g) BHEPL(h) 本文

(a′) 原圖(b′) BBHE

(c′) MMBEBHE(d′) BHEMHE

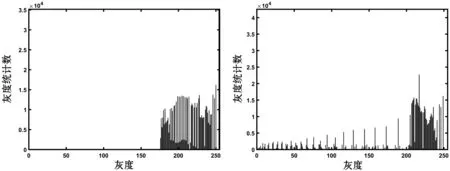
(e′) DSIHE(f′) RMSHE

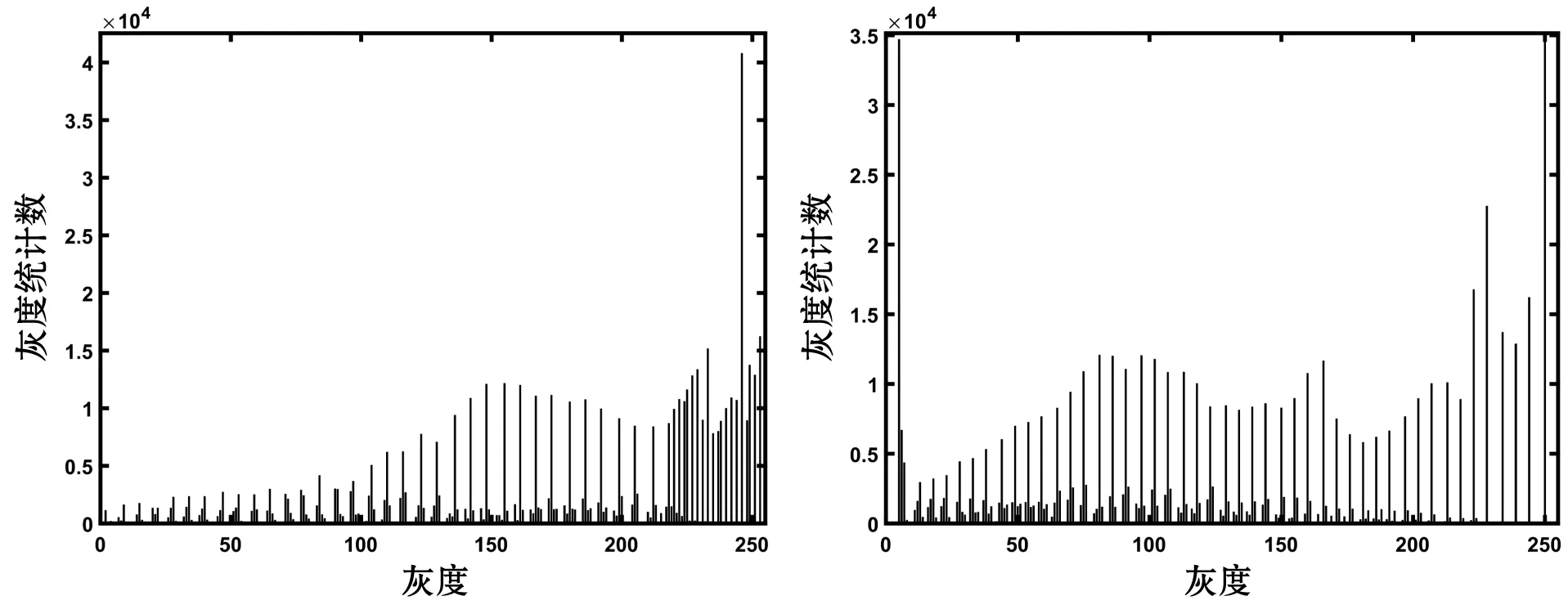
(g′) BHEPL(h′) 本文圖7 增強效果與直方圖

從圖7增強效果看，BBHE、BHEMHE、RMSHE、BHEPL和本文算法對原圖都起到了增強與去霧效果，DSIHE和MMBEBHE效果較差，且MMBEBHE有色斑。從圖像層次及去霧細節看，BBHE、BHEMHE、RMSHE、BHEPL及本文的5種算法中，本文去霧效果最優、細節層次更豐富，例如河岸兩邊樹木與橋后面的樹木都清晰可見。從表3的信息熵數值大小比較，本文信息熵最大(6.55)表明本文細節最豐富。

表3 實驗3結果數據

(4) 實驗4：正常動態范圍的紅外圖像如圖8所示。

(c) MMBEBHE(d) BHEMHE

(e) DSIHE(f) RMSHE

(g) BHEPL(h) 本文

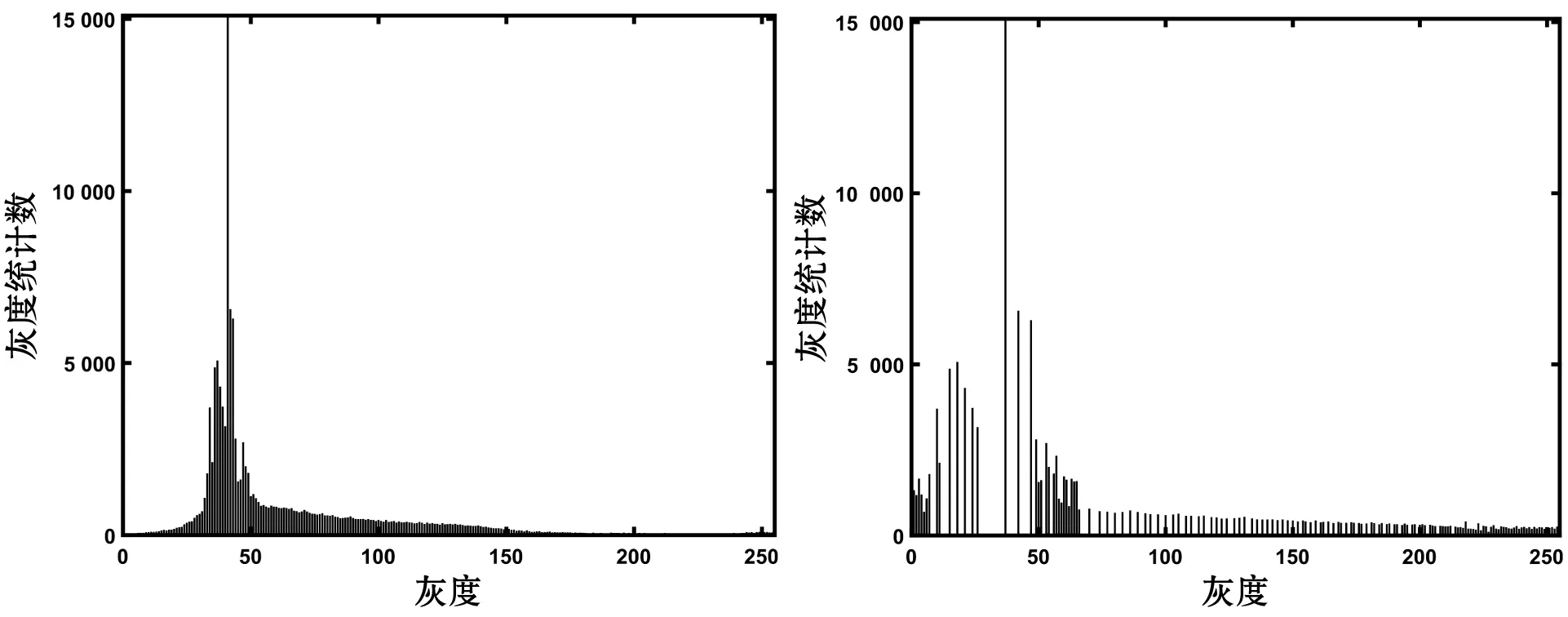
(a′) 原圖(b′) BBHE

(c′) MMBEBHE(d′) BHEMHE

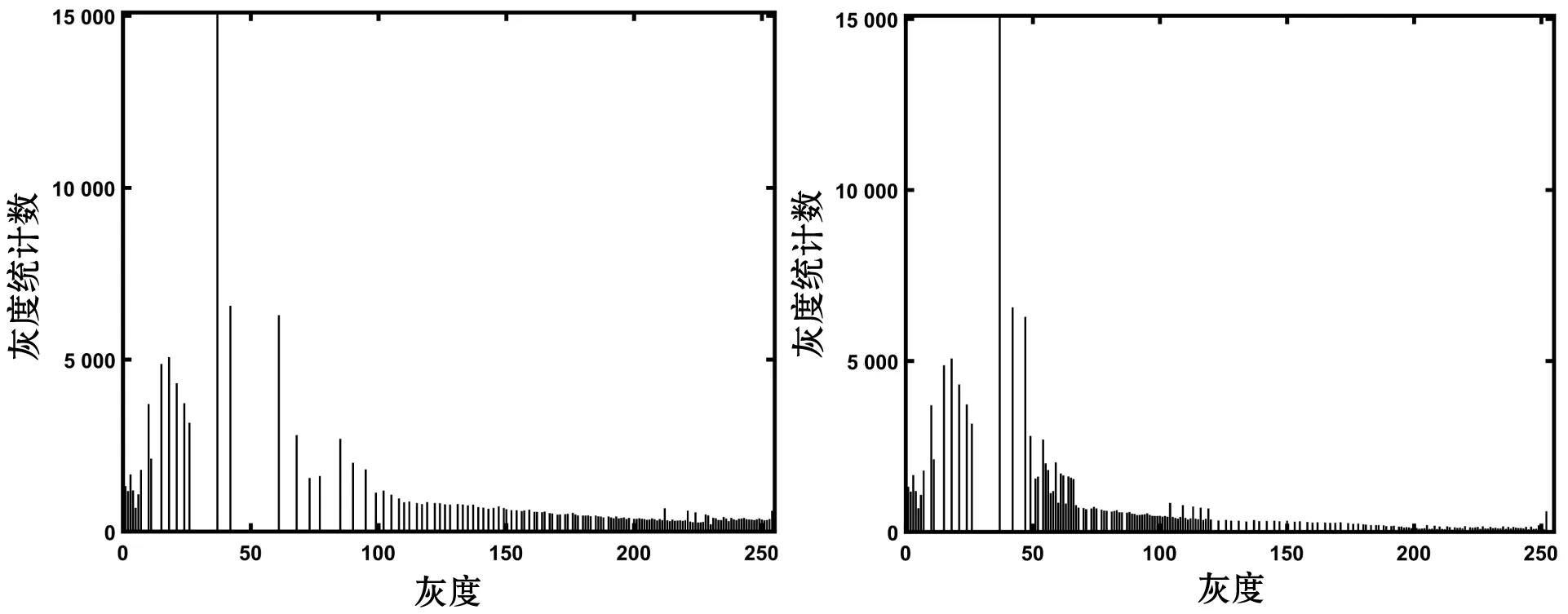
(e′) DSIHE(f′) RMSHE

(g′) BHEPL(h′) 本文圖8 增強效果與直方圖

圖8為紅外焦平面探測器探測出的紅外圖像，從增強視覺效果看，BBHE、MMBEBHE、BHEMHE、DSIHE、 RMSHE與BHEPL增強的圖像在暗區域存在過增強，視覺感覺上出現明顯“發白”的塊效應，例如圖像天空中出現發白現象。與前面6種算法相比，本文算法增強的紅外圖像，暗區域沒有出現過增強的塊效應，視覺效果最好；表4的客觀指標也顯示，本文算法的信息熵最大，信噪比排名第二，表明了本文算法增強的紅外圖像噪聲抑制較好、細節信息最豐富。

表4 實驗4結果數據

綜上所述，不管圖像的動態范圍處于何種位置，本文算法都能有效提高圖像對比度與清晰度，大大改善圖像視覺效果。從表5的60幅圖像增強結果數據看，七種算法中，本文算法的信息熵指標始終保持第一，在增強圖像的同時又充分展現了本文算法優越的細節信息保持性能。

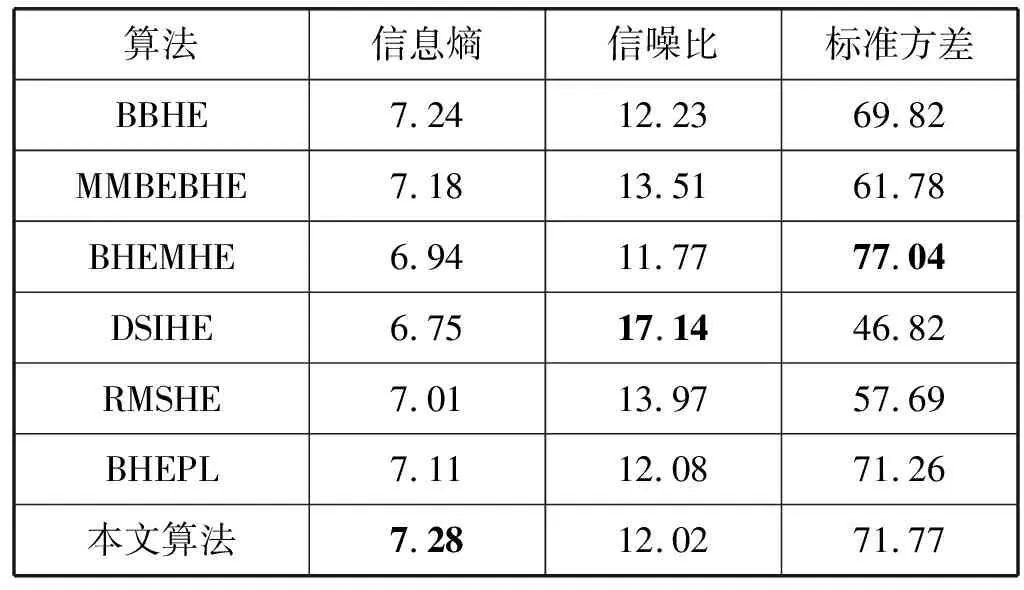
表5 60幅圖像平均結果數據

3 結 語

本文提出了一種直方圖受限的窄動態范圍的彩色圖像增強方法，無論彩色圖像的動態范圍是在低段(如低照度圖像)、中段或高段(如曝光過亮圖像)，該方法都能夠自動將窄動態范圍的彩色圖像調節到最大動態范圍[0,255]。算法能夠在提高圖像對比度的同時，不僅輸出圖像中的信息熵保持最大，而且達到了人眼視覺最佳觀看效果。本文算法的創新性主要是：通過圖像直方圖的累積概率分布閾值CT將原圖像直方圖分割成2個獨立的直方圖(圖2中的H1和H2)，再將H2(受限的直方圖)非線性映射至H1的均勻分布直方圖中。雖然該算法是基于直方圖的方法，但是和先前算法不同的是不需要作直方圖均衡。實驗結果表明，使用該方法得到的增強圖像信息熵值最高，彩色圖像的細節最為豐富。同時，算法還可以根據用戶需求，選擇不同的參數CT調節輸出圖像的對比度大小與細節豐富程度，可應用于視頻監控、數字機頂盒等視頻處理設備。