基于多示例遺傳神經網絡的室內PM2.5預測

陳 成 吳宏杰,2* 柳維生 傅啟明 湯 燁

1(蘇州科技大學電子與信息工程學院 江蘇 蘇州 215009)2(蘇州大學江蘇省計算機信息處理技術重點實驗室 江蘇 蘇州 215006)3(蘇州市立醫院(北區) 江蘇 蘇州 215000)

0 引 言

近年來，隨著我國工業化和城市化進程加快，空氣質量逐漸成為一個百姓關注的熱點問題。在眾多的空氣污染物中，PM2.5由于粒徑小、活性強且易附帶有害物質，成為我國環境空氣污染的重要污染物之一。現有的空氣污染監測與預測主要關注室外空氣質量。但是，人們每天在室內環境中停留時間占一天的80%以上，年老、幼小及患有慢性病的人群在室內停留更久的時間[1]，室內空氣污染往往比室外空氣污染對人體造成更持久的危害[2]。PM2.5對人體健康的影響包括損害呼吸系統、致癌、破壞人體免疫系統等[3-4]，這提示著人們室內環境與人群健康密切相關。因此，研究室內外空氣中PM2.5的監測和預測有重大的科學意義和現實意義。

經驗模型和統計模型是早年對空氣質量進行預測的主要方法，隨著大氣物理、化學機制研究的發展，機理模型逐漸取代之前的預測方法。在基于機理模型的空氣質量預測方法研究中，主要的思路是對污染物在空氣中的傳播、擴散、化學反應等過程實施抽象模擬，通過研究大氣污染物的物理化學特性及其在特定條件下的轉化規律，對未來的空氣質量狀況做出預測[5-6]。目前國內外使用的空氣質量預測模型一般是機理模型[7]，但是對于我國室內空氣的重要污染物之一PM2.5來說，其來源具有多樣性且其形成機理較為復雜，研究其在室內空氣中的擴散及復雜的轉化機理并進行有效的建模難度較大[8]。同時，在實際條件下，多種因素都可能影響空氣中污染物的含量，如溫度、濕度、光照等，所以空氣中污染物的含量具有很高的復雜性和不確定性。而隨著人工智能的發展，很多研究者開始嘗試使用機器學習方法來進行空氣質量預測的研究。如Feng等[9]提出了一種將PM2.5軌跡分析與小波變換相結合的混合模型，以提高人工神經網絡預測PM2.5的平均預測精度；Yegaeh[10]將局部最小二乘方法與支持向量機方法結合對CO的日均值進行了預測，Garcia[11]利用支持向量回歸方法對臭氧濃度進行了小時級預測。為了提高預測模型的精度，Kamali[12]提出一種通過譜分解構建的模型預測空氣污染物濃度，通過Kolmogorov Zurbenko濾波器得到的人工神經網絡(ANN)，用于分離和單獨預測空氣污染物短期、季節和長期時間序列的三個光譜成分。盡管上述單示例方法在空氣質量預測上取得了一定的效果，但是仍然存在兩個問題：第一，樣本采集粒度與預測粒度不一致，導致單示例方法難以準確描述本問題的實質；第二，對室內PM2.5預測的重要特征研究不足。因此上述方法預測精度難以進一步提高。且以上研究方法大多使用小時級測量的數據作為訓練樣本，忽略了小時內連續時刻的污染物數據隱藏的序列關系，導致最終預測的小時級污染物濃度不夠準確。

基于此，本文提出一種基于多示例遺傳神經網絡的室內外PM2.5實時預測方法，將遺傳神經網絡與多示例方法結合，用遺傳神經網絡構建深層次預測模型，利用多示例機制將小時內的多個連續數據進行融合來挖掘其時序特征，最終提高了室內PM2.5小時級預測的精度。室外預測模型中以時間戳、溫度和相對濕度作為輸入特征，室內預測模型中選取與室內PM2.5密切相關的氣溫、相對濕度等屬性作為輸入特征。同時，研究表明[13]，當室內無內擾動及污染源時，由室內外環境條件和外窗等特性決定的通風率成為影響室內PM2.5的重要因素，因此將通風率也作為一項模型輸入特征。最后通過對醫院辦公室內外歷史空氣質量數據進行分析和深度挖掘，構建預測模型并進行了驗證。

1 基于多示例遺傳神經網絡的PM2.5預測方法

1.1 數據采集與特征選取

分別于測試房間室內外設置監測點，室外監測點布于醫院大樓3層，室內監測點布于1.5米呼吸帶區域。我們分別于2017年7月、10月和2018年1月，即夏季、秋季、冬季3個季節采集連續的7天數據，形成3個數據集。采樣間隔為全天24小時每隔1分鐘進行一次采樣，所采集數據分別為室內外氣溫(單位：℃)、室內外相對濕度(單位：%)以及室內外PM2.5(單位：μg/m3)，每個樣本集包含9 600條數據，同時把時間戳也作為模型輸入特征之一。分別定義如下室外和室內預測模型。

moutdoor=F(t,wout,sout)

(1)

mindoor=F(t,pout,win,wout,sin,sout,v)

(2)

對于室內模型，當前室內的PM2.5與當前室內外溫度、相對濕度、室外PM2.5以及通風率共7個參數有關[14]，對應于示例子網的7個輸入，而當前室內PM2.5對應于每個包的輸出。每個數據集中以9 000條樣本數據作為網絡的訓練集，600條數據作為測試集，室外和室內模型示例子網的特征輸入如表1所示。

表1 室內外模型輸入特征數據表

v表示當前房間室內通風率，計算公式如下：

v=s×|wout-win|

(3)

式中：s是為窗口打開的面積，wout為室外溫度，win為室內溫度。在實驗前先對樣本進行歸一化處理，歸一化公式如下所示，使之分布在[-1,1]之間。

(4)

1.2 基于多示例遺傳神經網絡的PM2.5預測模型

多示例框架下的遺傳神經網絡可由圖1來描述。我們把N個樣本作為N個包數據，把1小時內每隔1分鐘所測的數據作為1個示例，則每個包中有60個示例。每個示例均為一個7維的特征向量，分別對應示例子網神經網絡的室內外溫濕度等7個輸入特征，記包Bi中的第j個示例為[Bij1,Bij2, … ,Bij7]T。圖中F1至F7表示表1室內特征所示的7個特征。

圖1 多示例遺傳神經網絡模型框圖

在多示例神經網絡的回歸學習問題中，包的實值標記是已知的[15-16]。因此，本文利用訓練包的實際輸出，在包的基礎上定義全局誤差函數為:

(5)

式中:Ei為包Bi對應的輸出誤差。

已有的相關研究指出[17]，在多示例學習問題中，包的實際輸出主要由包中示例的最大實際輸出所決定。將包Bi的誤差定義為:

(6)

式中:Ei為示例Bij經過模型得到的預測值。

神經網絡隱藏層節點數的設置至今還沒有確定的指導方法[18]，試湊法是比較常見的方式。通常是使用不同的隱藏層節點數構建多個網絡，分別對同一組訓練數據進行訓練，取最優模型的隱藏層節點數作為最佳網絡參數。

也有研究者總結出一些經驗公式[19]，用來計算可能的隱藏層節點數目，把它設成試湊法的起始數值。常用的經驗公式為：

(7)

式中:j、l、k分別對應輸入、輸出、隱藏層神經元數目，ξ為1到10 范圍內的整數。綜合前文分析，本實驗中的示例子網輸入層節點數為7，即j為7，輸出層節點數為1，即l=1，根據式(7)可算出該神經網絡隱藏層的節點數范圍是3到12。經過多次實驗對比論證，當隱藏層節點數k為11的時候，該多示例遺傳傳神經網絡模型能得到最佳的預測結果。

1.3 多示例遺傳神經網絡預測流程

多示例遺傳神經網絡預測算法流程如圖2所示。

圖2 多示例遺傳神經網絡訓練算法流程圖

在圖2所示的訓練流程中，初始化網絡結構包括每個包的多個示例子網中的前向神經網絡結構，每個包的輸出變量為預測的PM2.5數據。同時，根據本文前述分析針對本項目的實際情況，多示例子網中的隱藏層節點數設置為11。

初始化種群中，對包中示例子網的權重和偏置進行實數編碼，然后求出種群中每個個體的適應度并進行評價，評價函數為誤差平方和的倒數，即Fitness=1/SSE。

(8)

若滿足進化結束條件則將當前權重和偏置作為示例子網的最優初始值來計算當前網絡的預測結果與實際值的誤差，并進行權重和偏置更新，否則產生新的種群繼續迭代尋優。迭代停止后，將全局較好解作為初始權值和偏置進行接下來的多示例神經網絡訓練。

多示例遺傳神經網絡的優化停止條件為如下兩個條件之一成立：

1) 運行到某一代時，全局誤差Ei小于預先給定的閾值；

2) 訓練次數達到預先設置好的最大訓練次數。

1.4 多示例遺傳神經網絡初始權值訓練算法

三層單元的神經網絡可以滿意地再現任何連續函數[20]，神經網絡具有自適應、自組織和實時學習的特點。常見的網絡一般都使用誤差導數來更新網絡參數，從原理上來看并不是全局尋優算法，在隨機初始化網絡權重和偏置的情況下很可能導致輸出結果陷入局部極小值點。

遺傳算法起源于自然界“優勝劣汰”法則，是一種全局尋優算法。區別于傳統優化算法的是，遺傳算法能同時處理種群中的不同個體并根據不確定性原則來引導算法搜索方向，極大地擴展了問題解的覆蓋面和搜索方向的多樣性，降低陷入局部極小值點的可能性。由此，可以使用遺傳算法來對示例子網的初始權值和偏置進行選取，以此來降低得到局部最小值的可能性，從而提高多示例框架下的神經網絡的預測性能，算法實現如下所示：

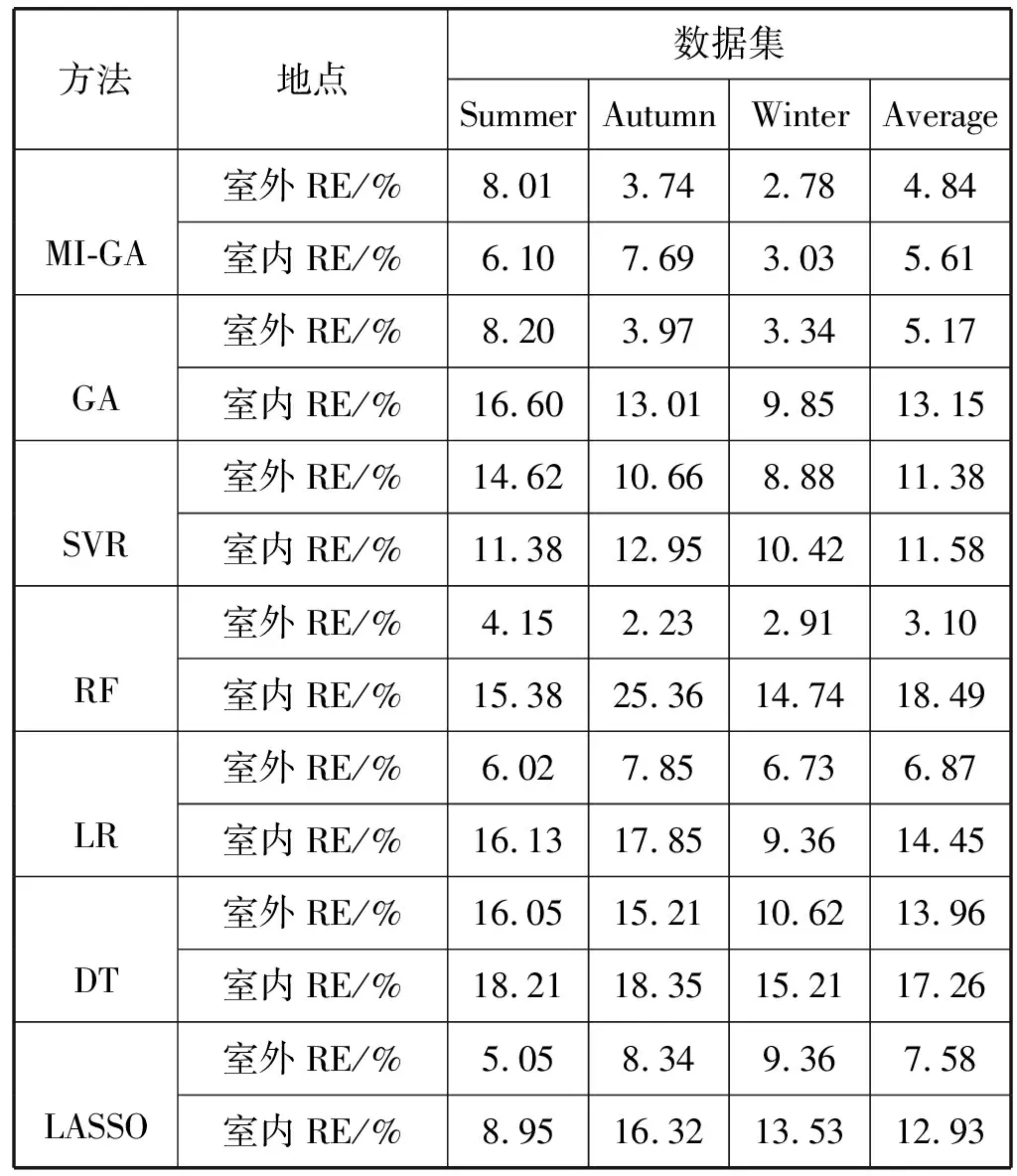
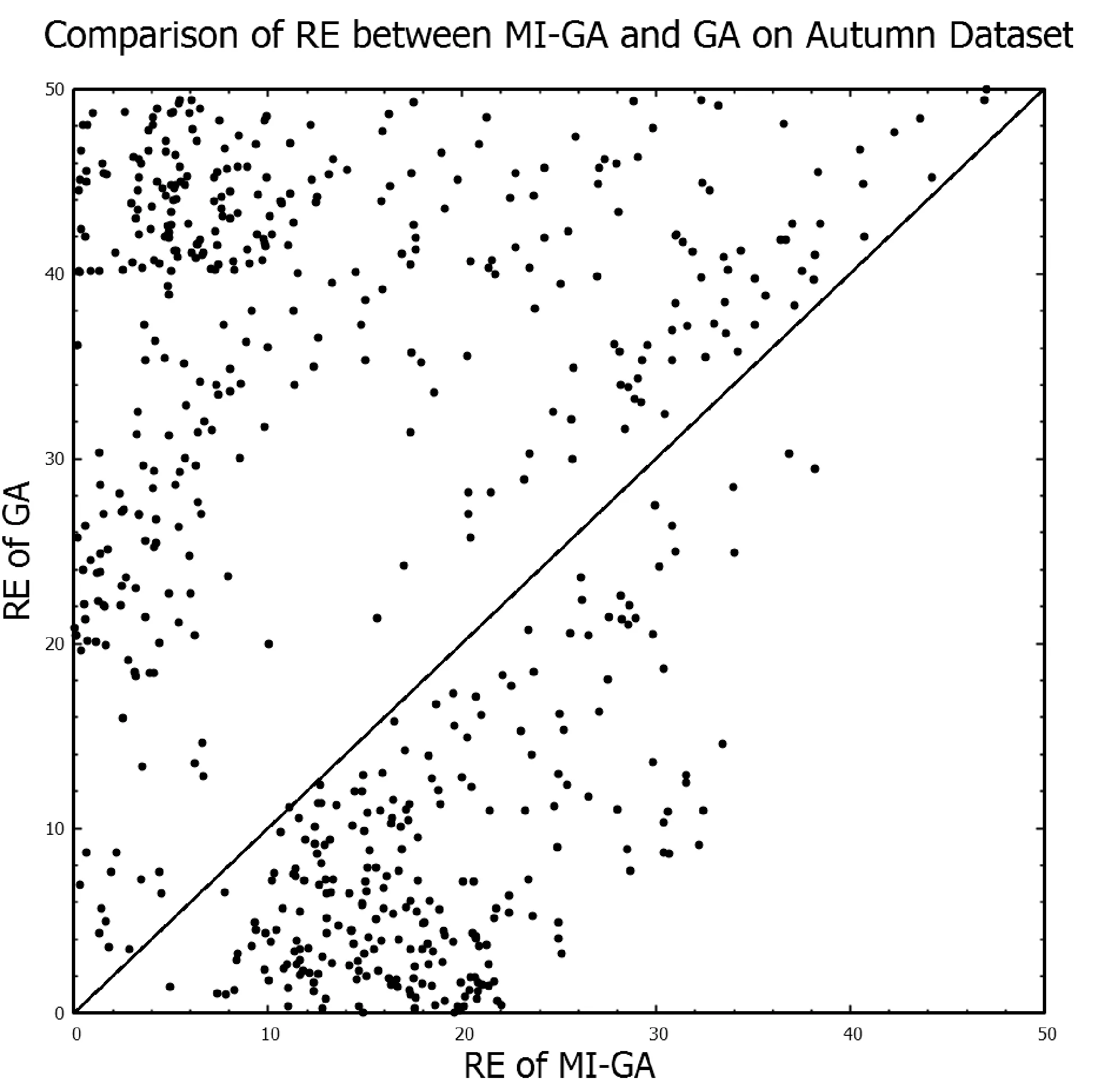
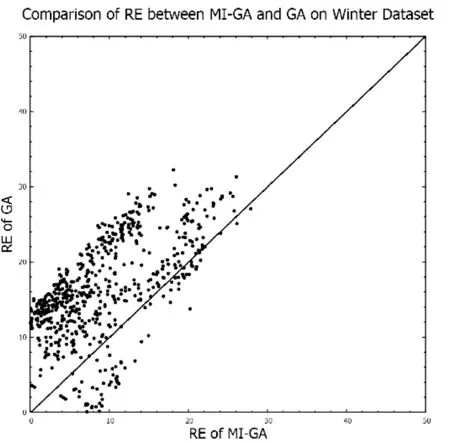
G:停止進化代數; Iter:繁殖代數 w:網絡的權重CalFitness:計算適應度;Copy:選擇個體進行復制;Crossover:交叉;Mutation:變異;M:個體個數;TN,Q:由N個包構成的數據集,每個包包含Q個示例1. Input: TN,Q2. Initialize(Sk, k=1,2,…,M)3. whileTrue4. w=Encoding(Sk)5. for(i=0; i

CalFitness(w,N,Q)用于按式(8)計算包的適應度函數。該算法的時間復雜度為O(M×G)，遺傳算法搜索最優權值的停止條件定義為如下兩個條件之一成立。

1) 運行到一定代數時，適應度函數中最高的適應度函數小于預先設定的閾值；

2) 進化次數增長到初始給定的最大進化次數。

2 結果分析

2.1 評價指標

多種指標可用于對預測模型的性能進行評價，其原理都是對標簽和預測值之間的差距進行分析。對于回歸問題來說，可以從2個方面來評價這種差異，分別是預測值與標簽之間在數值上的偏差，以及二者的一致性程度。因此，本文采用2種指標對預測結果進行評價，分別是相對誤差RE(Relative Error)、和擬合指數IA(Index of Agreement)[22]，RE反映了預測值與標簽之間在數值上的偏差，IA反映了預測值與標簽之間的一致性，可以用來表示模型預測的效果，計算公式如下：

(9)

(10)

2.2 結果與分析

根據式(9)和式(10)可知，RE是越小越好，IA是越大越好。表2是多示例遺傳神經網絡算法MI-GA(Multi-Instance Genetic Neural Network Algorithm)、遺傳神經網絡算法GA(Genetic Neural Network Algorithm)、支持向量回歸(Support Vector Regression)、隨機森林(Random Forest)、線性回歸(Linear Regression)、決策樹(Decision Tree)、LASSO(Least Absolute Shrinkage and Selection Operator)，在室外和室內的3個測試集(每個測試集為600條數據)上預測所得結果的平均相對誤差RE的比較，表3為這七種方法在是否加“通風率”特征的實驗比較。

表2 室內和室外預測結果相對誤差(RE)比較

表3 MI-GA 與其他六種方法在室內數據上預測結果比較

續表3

(1) 室內與室外預測比較：

從表2中可看出，在對室內和室外PM2.5的預測中，對同一種方法，室外預測結果的相對誤差RE都要小于室內預測結果，這是因為室內PM2.5來源復雜，相較于室外PM2.5而言更加難預測。在對室外PM2.5的預測中，本文提出的MI-GA方法獲得了僅次于RF的預測結果，這是因為本文實驗中，室外特征較少，而在特征較少和小數據集的情況下，相對于其他算法， RF能發揮更大的優勢。而相對于GA、SVR、LR、DT、LASSO，MI-GA方法取得了更好的預測效果，平均RE降低了0.33%、8.31%、2.03%、9.12%和2.74%。對于難度較大的室內PM2.5的預測，因為特征由3個增加到7個，MI-GA方法取得了最好的預測效果，相較于GA、SVR、RF、LR、DT和LASSO，平均RE分別降低了7.54%、5.97%、12.88%、8.84%、11.65%和7.32%。

(2) 特征是否含通風率實驗比較：

窗戶是連接室內和室外的重要通道，通風情況是影響室內PM2.5的一個關鍵因素，因此，通風率成為預測室內PM2.5的一個重要特征。本文對室內的3個數據集進行了是否含“通風率”特征的實驗比較，實驗結果見表3。從表3中可看出，在加入“通風率”特征的情況下，七種方法預測結果的相對誤差RE分別降低了1.93%、0.04%、12.02%、3.93%、3.89%、3.77%和8.09%，擬合指數IA提高了0.07、0.10、0.01、0.04、0.06、0.10和0.06。實驗結果證明了“通風率”特征對于預測室內PM2.5的重要性，為今后的模型改善提供了一個新思路，同時也可以為其他相關專業研究人員提供新的參考特征。

2.3 MI-GA方法與其他六種方法預測結果比較

從表3中可見，在加入“通風率”特征的結果中，本文提出的MI-GA方法預測結果RE為5.60%，比GA降低7.55%，比SVR降低5.98%，比RF低8.36%，比LR低7.66%，比DT低14.69%，比LASSO低8.21%。可見，使用多示例機制將預測時間與采樣間隔時間有效融合后的遺傳神經網絡預測模型，預測結果的相對誤差得到了很好的降低。

圖3為MI-GA與GA方法在3個室內數據集(包含“通風率”特征)上所得結果相對誤差分布的散點圖。從圖中可以看到，分布于對角線上方的數據點都要多于直線下方的數據點，即相較于GA方法所得結果中，MI-GA方法所得結果中相對誤差RE較大的點要更少，即MI-GA方法預測結果中有更多的數據比較接近標簽。

(a) Summer數據集預測結果

(b) Autumn數據集預測結果

(c) Winter數據集預測結果圖3 MI-GA與GA方法在三個數據集上的RE比較散點圖

圖4為測試樣本在六種方法上預測結果在不同誤差區間內的分布直方圖。從圖中可以看出，本文提出的MI-GA方法在室內數據集預測結果中，RE低于5%的樣本個數有517個，比GA方法多339個，比SVR方法多252個，比RF方法多226個，比LR方法多92個，比DT多194個，比LASSO多138個。而在RE大于30%樣本中，MI-GA方法的樣本點最少，由此可見MI-GA方法不僅具有較高的預測準確度，還具有很好的穩定性。MI-GA能取得更好的預測結果，原因可能是多示例神經網絡方法將某個時間范圍內的多條數據集中于一個包中，充分考慮了包中各個示例之間隱藏的關系，進而更深層地挖掘出PM2.5的序列特征，從而提高預測的精確度。

圖4 不同RE區間內樣本分布直方圖

3 結 語

綜合以上對多示例遺傳神經網絡模型的分析和實驗的實現，表明以時間戳、溫濕度、通風率以及室外PM2.5等因子作為網絡的特征輸入，可以較為準確地預測出室內的PM2.5。最后從醫院房間采集了28 800條數據進行實驗驗證，結果顯示相對誤差為5.60%，比傳統遺傳神經網絡降低7.55%，比支持向量回歸方法降低5.98%，比隨機森林低8.36%，比線性回歸低7.66%，比決策樹低14.69%, 比LASSO回歸低8.21%。這樣的結果對于醫院房間內預警污染的發生是可行的。

本文中所采用的遺傳算法是最基本的遺傳算法，遺傳算法的設定在一定程度上會影響神經網絡參數的優化，所以如何對遺傳算法做進一步的改良或者選取更優的進化算法，進而優化多示例神經網絡的模型結構，從而降低預測模型的誤差率將是我們下一步的研究方向。同時，醫院室內空氣質量的預測是一種小范圍問題，接下來的工作將考慮到將算法用于住宅、教室等更為復雜的環境，進一步驗證算法的性能。