DARPA2潛艇模型非定常流動粘性流場和水動力計算

于向陽，姚凌虹，孟慶昌，劉巨斌，張志宏

(1. 海軍航空大學青島校區，山東 青島 266000；2. 海軍工程大學，湖北 武漢 430033)

0 引 言

潛艇水下操縱性能研究，與潛艇的安全航行密切相關，是其進行戰術機動的重要保證，同時有著直接的作戰應用背景。實際航行中的潛艇是一種復雜運動的組合體。一方面，其高速、大攻角及強機動的運動特征，使其呈現出非定常性與強非線性；另一方面，潛艇作有攻角機動時，即使攻角保持不變，由于邊界層分離產生漩渦，流動仍然會呈現出非定常特征。這就給理論和試驗研究帶來了很大的困難，采用數值模擬是切實可行的研究方法[1–3]。

本文以DARPA2潛艇模型為研究對象，采用基于非結構化網格的有限體積法，數值求解非定常、不可壓縮的RANS方程，湍流模型采用SA模式，在SA模式中，速度-壓力耦合SIMPLE方法處理，對流項采用2階迎風格式，非定常項采用2階精度離散，隱式迭代求解方程組，非穩態迭代時間步長=2.322 4×10–3s（無量綱時間步長=3.73×10–2），步進200歩，非穩態流場速度由UDF給定，得到非定常粘性流場和水動力數值計算結果，并與文獻[1]的實驗結果進行對比。

1 數值離散方法

采用CFD軟件數值求解DARPA2潛艇模型粘性流場和水動力，采用基于非結構化網格的有限體積法，數值求解非定常、不可壓縮的RANS方程。

湍流模型采用SA模式，在SA模式中，生成項所采用的形式為：

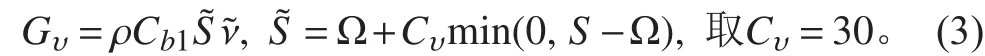
速度-壓力耦合采用SIMPLE方法處理，對流項采用2階迎風格式，非定常項采用2階精度離散，隱式迭代求解方程組。計算雷諾數Re=5.52×106，初值收斂準則為所有求解變量的無量綱殘差下降4個量級，非穩態迭代時間步長=2.322 4×10–3s（無量綱時間步長=3.73×10–2），步進200歩，模型的運動狀態由UDF定義。

1.1 計算模型

計算對象為DARPA2潛艇模型（見圖1），模型主要參數如表1所示，包括艇主體、指揮臺圍殼、尾附體。數值計算在慣性坐標系中進行，采用直角坐標系，原點取在模型頭部頂端，x軸與艇體的對稱軸重合，方向與無攻角時來流方向一致，z軸豎直向上，y軸水平，計算時直角坐標系保持為模型處于零攻角時的位置，當模型作操縱運動時，坐標不變，而模型與坐標系產生相對運動；在所定義的坐標系下， 規定來流的z方向速度分量正時為正攻角，初始攻角為0°。

圖 1 全附體DARPA2模型Fig. 1 DARPA2 submarine model with sail and stern appendages mounted

表 1 DARPA2潛艇模型主要參數Tab. 1 DARPA2 model scale

考慮到模型本身的對稱性，同時操縱運動僅為xz面內的非定常回轉運動，在不影響數值計算的準確性前提下，僅對半艇體流動進行數值計算，以減少計算量；計算域為半圓柱體區域，范圍：–2.0≤x/L≤5.2，–2≤z/L≤2，0≤y/L≤2，其中 L為艇體長度，L=2.236 m，計算域如圖2所示。

圖 2 模型的邊界條件設置Fig. 2 Boundary setting of the computational domain

1.2 邊界條件

邊界條件設置可分為初始流場狀態和非穩態運動狀態2個階段。

初始邊界條件（見圖2）：半圓柱體的左半圓面AEB（x/L=–2.0處）定義為速度入口，給定速度大小和方向；半圓柱體的右半圓面DFC（x/L=5.2處）定義為壓力出口；半圓柱面的上、下兩部分（EBCF/AEFD），及主體、指揮臺圍殼、尾附體，定義為無滑移壁面，速度分量和湍動能為0，以加速收斂，獲得較好的初值；對稱面上，法向速度分量為0，平行于對稱面的速度分量的法向導數和所有標量的法向導數為0；初始攻角為0。

非穩態時模型作操縱運動，攻角發生改變，變化范圍由0°～–25°，須調整邊界條件，以適應運動狀態的變化，此時定義半圓柱面的上半部分EBCF（z＞0）為速度入口；半圓柱面的下半部分AEFD（z≤0）為壓力出口，考慮到在迭代過程中，有可能存在數值上的反向流動，設置出口回流方向的方式為垂直于出口面；由于采用慣性坐標系，體網格是運動的，定義體網格和物面旋轉中心（0.659 62，0，0）和旋轉軸y軸，角速度由UDF定義。角速度曲線，具體描述如如圖3及表2所示（實驗數據來自文獻[1]）。

1.3 網格設置

體網格采用基于四面體的非結構化網格形式，邊界層網格進行加密處理，網格密度由模型表面至遠場由密到疏分布。

圖 3 角速度ω隨時間變化曲線Fig. 3 ω vs. time

表 2 不同模型的角速度函數Tab. 2 The function of ω for different model

表 3 網格主要參數Tab. 3 The grids for simulation

考慮到對模型進行非穩態運動模擬時，網格動態變化，網格需要均勻銜接，以避免網格的奇異變化導致迭代不收斂。

2 動態邊界處理

本文中應用動網格技術處理含有動態邊界問題的非穩態運動狀態，邊界運動由UDF定義。

2.1 UDF編寫

用戶自定義函數UDF（User-Defined Function）是CFD軟件提供的一個用戶接口，使用者可以通過它與CFD軟件的內部數據進行交流，方便用戶解決一些標準的CFD軟件模塊不能解決的問題[4–6]。

圖 4 攻角–25°物面（model-1）Fig. 4 for the wall at –25° （model-1）

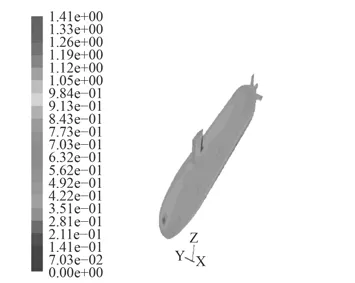
圖 5 攻角–25°物面 （model-2）Fig. 5 for the wall at –25° （model-2）

本文考慮到非穩態問題的復雜性，以及計算機本身的運行環境（已安裝Visual Studio C++ 開發軟件），采用編譯的UDF定義其運動（非穩態場的角速度函數），以提高執行速度[7]。

2.2 網格更新

動網格模型，即在每一個時間歩迭代之前，根據邊界或物體的運動和變形來更新和重新構建計算域網格，從而達到求解非定常問題的目的[8–10]。而邊界的形變和運動由UDF加以定義。計算中的網格更新情況如圖6所示。

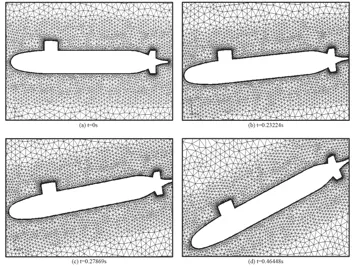
圖 6 網格更新示意圖（model-1）Fig. 6 The view of mesh motion （model-1）

由圖6可知，艇體和附體的物面邊界層都參與了網格的重構過程，網格質量沒有受到影響，網格更新過程中沒有負體積和大長寬比網格出現，從而保證了數值迭代的延續。

3 初始流場計算

為了得到較好的非定常結果，需要對初始流場進行討論。本文中非定常因素，一方面，大攻角時，分離流動導致伴隨渦的出現；另一方面，給定的模型運動狀態，即角速度的定義本身就是隨時間變化的函數。圖7給出不同計算參數和邊界條件下的初始流場變量收斂曲線。最初，分析初始時刻時，沒有過多地考慮零攻角的流場特征，將邊界條件半圓柱面的上、下兩部分（EBCF/AEFD）分別定義為壓力出口和速度出口，在迭代過程中流場變量波動起伏，近似周期性變化，但收斂精度未達到要求，如圖7（a）所示；分析上述收斂精度持續不下的情況，可能是松弛因子過大的原因，將部分松弛因子降低30%，流場變量的波動情況消失，但收斂精度未出現改觀，如圖7（b）所示；觀察到速度分量殘差未發生變化，追溯根源，可能是邊界條件有待優化，在圖7（a）所定義的邊界條件的基礎上，將半圓柱面的上、下兩部分（EBCF/AEFD）分別定義為無滑移壁面，速度分量殘差迅速收斂，如圖7（c）所示；圖7（d）再次調整部分松弛因子，流場變量在925次迭代后達到收斂精度。

4 時間步長選取

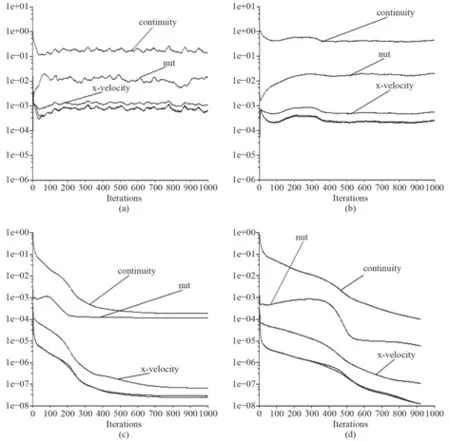
圖 7 初始流場變量收斂歷史Fig. 7 Convergence history of flowfied variables

初始流場由零攻角定常結果給出，進行非定常計算時需給定時間步長。依據文獻[1]中的模型實驗，給定角速度隨無量綱時間t'的變化關系如圖8所示，無量綱時間定義為，無量綱時間取值范圍0～7.463 7時，對應的有量綱時間為0～0.464 48，計算時采用有量綱時間進行計算，非定常攻角范圍0～–25°，考慮到時間步長對數值計算結果的影響，認為10–3s數量級已滿足計算精度的要求。

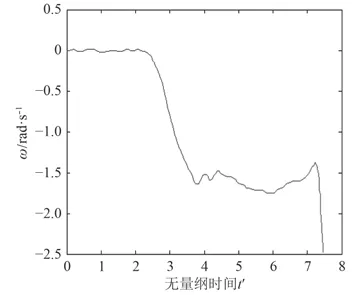
圖 8 角速度ω（rad/s）隨無量綱時間變化曲線Fig. 8 ω（rad/s） vs. non-dimensional time

5 計算結果分析

應用表2中的3種模型曲線，對模型運動進行定義。初始化流場后，進行非定常數值模擬。

為追求曲線擬合的精確性，采用最小二乘法高階多項式擬合實驗數據，如圖3（model-3）所示，當n=18時，除波動較復雜的拐點處略有差別外，整條曲線基本重合；但進行非定常數值計算時，角速度給定值持續增加，在不到100歩的迭代過程中，迭代時間不到半數，殘差竟迅速增至102數量級，超出預定值近100倍，最后導致計算結果發散。分析原因，認為是時間精度不夠的原因，將時間步長下降一個量級后，結果仍舊如前所述。嘗試時間步長的一味降低，勢必導致計算量的增大。

重新分析計算結果發散的原因，非穩態問題本身需要進行空間和時間的離散，變量之間的耦合關系將導致非線性增強，同時高階曲線擬合容易造成較大的截斷誤差，綜合上述原因，應用model-2，降低多項式階次擬合實驗數據，以驗證是否是截斷誤差過大導致結果發散；非定常結果穩定，且角速度按給定值正常迭代。

但model-2對實驗數據擬合效果不夠理想，需要尋找其他函數，進行數值計算。本例采用model-1對實驗數據進行擬合，同時略去角速度變化較大的尾端，擬合效果較好，數值計算結果穩定。

5.1 水動力分析

圖9給出了模型進行非定常數值計算時，升力系數CL隨時間的變化情況。圖中曲線unsteady，Quais-Steady+Time Lag和Quais-Steady為文獻[1]中的實驗結果，曲線unsteady為某一次非定常試驗結果，Quais-Steady+Time Lag為20次非定常試驗結果的平均值，Quais-Steady為準定常狀態下的試驗結果。

圖 9 升力系數與時間的關系Fig. 9 Normal force development against time

從圖中可以看到，定義相同的運動狀態，unsteady的升力系數卻表現出較強的不確定性，Quais-Steady+Time Lag曲線在描述unsteady曲線時符合程度也存在較大的偏差。分析上述問題產生的原因（參考圖3），本文在對實驗所定義的運動曲線的模擬上也存在局限性；同時，不得不指出非定常試驗本身所具有的不確定性因素，如風洞中溫度、風速的變化、及氣流對操縱運動裝置的影響（易使模型發生振動）等，隨著時間的變化，流場中物理量的變化容易受到這些不確定因素的影響。

比較2種模型的數值計算結果，升力系數隨時間變化平穩，在前0.25 s與實驗值符合較好；模型model-1對升力系數的計算值在中間段（0.15～0.25 s）有較明顯的減小過程（參考圖3），這與model-1所定義的角速度曲線在中間段有一個負向加速過程相對應；模型model-2在初始階段，升力系數由正轉負，是與其所定義的角速度值在初始階段大于0相一致的；要取得與實驗一致的模擬效果，由實驗中的不確定因素產生的誤差需要加以考慮。

5.2 粘性流場分析

圖10～圖13給出了分別采用2種模型得到攻角–25°時物面壓強系數和物面切應力系數的數值計算結果，兩者在物面上的連貫性和均勻性均較好，在迎風處出現極值，這與理論上此處對應速度的最小值是相符合的。與定常攻角–25°（見圖14和圖15）時的結果相比，在變化趨勢和數值分布上一致。

圖16給出了攻角–25°時x/L=0.863截面速度向量圖（model-1），在背風面可以清晰地看到有分離渦出現，反映了流場的粘性分離特性。

6 結 語

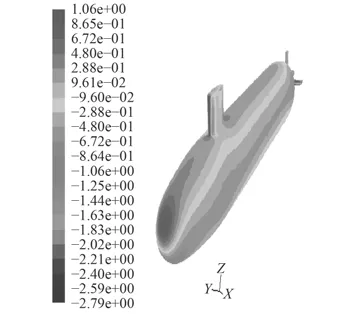
圖 10 攻角–25°物面壓強系數（mode-l）Fig. 10 Surface pressure cofficient at –25° （mode-2）

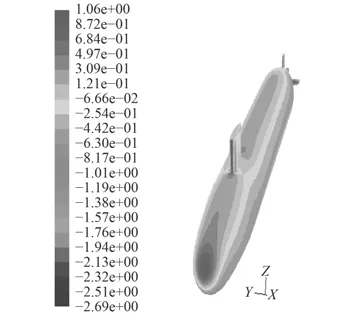
圖 11 攻角–25°物面壓強系數（mode-2）Fig. 11 Surface pressure cofficient at –25° （mode-1）

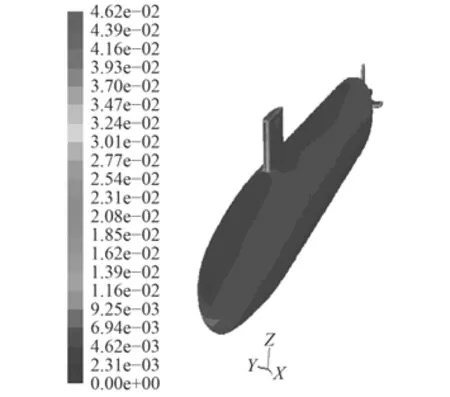
圖 12 攻角–25°物面剪切力系數（mode-l）Fig. 12 Surface friction cofficient at –25° （mode-l）

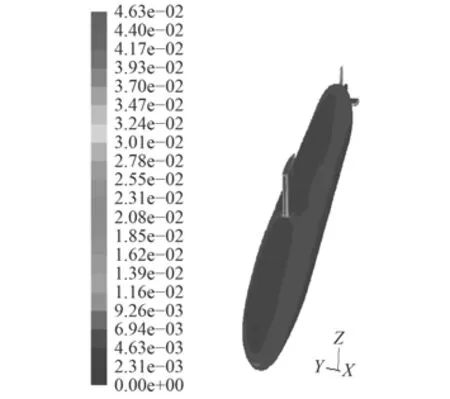
圖 13 攻角–25°物面剪切力系數（mode-2）Fig. 13 Surface friction cofficient at –25° （mode-2）

圖 14 攻角–25°物面壓強系數Fig. 14 Surface pressure cofficient at –25°

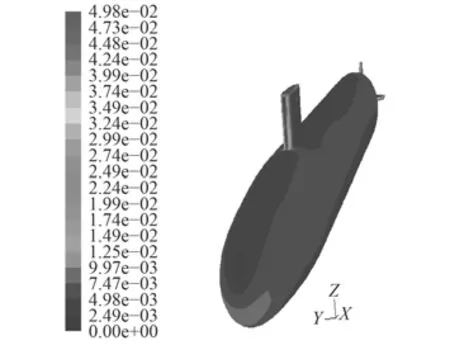
圖 15 攻角–25°物面切應力系數Fig. 15 Surface friction cofficient at –25°

采用CFD軟件數值求解非定常的DARPA2潛艇模型粘性流場和水動力，采用基于非結構化網格的有限體積法，數值求解非定常、不可壓縮的RANS方程，湍流模型采用SA模式，在SA模式中，速度-壓力耦合采用SIMPLE方法處理，對流項采用2階迎風格式，非定常項采用2階精度離散，隱式迭代求解方程組，非穩態迭代時間步長=2.322 4×10–3s（無量綱時間步長=3.73×10–2），步進200歩，非穩態流場速度由UDF給定。采用編譯的UDF定義其運動（非穩態場的角速度函數）。

為了得到較好的非定常結果，需要對初始流場進行討論。通過調整邊界條件和部分松弛因子，初始流場變量在925次迭代后達到收斂精度。

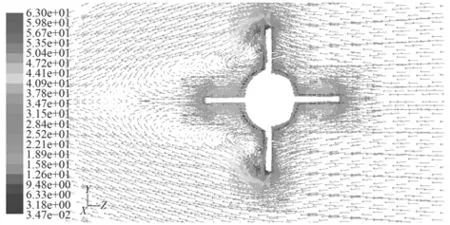
圖 16 攻角–25°時x/L=0.863截面速度向量圖Fig. 16 Velocity vector diagram at x/L=0.863 section and –25°angle of attack against time

在初始流場穩定的基礎上，應用表2中的3種模型曲線，分別定義運動狀態，進行非定常數值模擬。過分追求曲線擬合的精確性，采用高階多項式擬合實驗數據導致將計算結果發散；降低多項式階次，得到穩定的非定常結果；采用model-1對實驗數據進行擬合，擬合效果較好，數值計算結果穩定。

要取得與實驗一致的模擬效果，由實驗中的不確定因素產生的誤差需要加以考慮。攻角–25°時物面壓強系數和物面切應力系數的數值計算結果，在壁面上的連貫性和均勻性均較好，與定常攻角–25°時的結果在變化趨勢和數值分布上一致。