亞里士多德的顯示法的擴展應用

杜鵬昊

（中央財經大學，北京 100081）

1 亞里士多德的三段論系統簡介

亞里士多德的三段論證明體系中，用現代邏輯理論來理解，是把第一格的四個式：AAA、EAE、AII、EIO作為他的證明系統中的公理。在亞里士多德最后的闡釋中，又把第一格的AII和EIO化歸為第一格的AII和EIO，所以亞里士多德的三段論證明系統中，最核心的公理只有第一格的AAA和EAE（盧卡西維茨，2009）。亞里士多德證明其他格的有效式主要用到了化歸法、歸謬法，僅在證明第三格AAI式OAO式時提及可用顯示法證明，而且能用顯示法證明的式也可以用其他的方法證明（張家龍，2004）。所以看似顯示法的作用并沒有多么廣泛，但是顯示法所運用的思想是非常巧妙的，而且顯示法也可以擴展應用到其他三段論式的證明中。

區別于傳統形式邏輯所認可的四個格，亞里士多德只把三段論系統分為三個格，根據張家龍先生（2004）的說法，亞里士多德把第四格的三個式劃歸為第一格的三個非標準式。之后，亞里士多德的學生德奧夫拉斯特把其數量擴充為五個，這個補充就是現在所說的第四格的有效式。所以，亞里士多德的三段論系統是可以擴充到第四格的，即使亞里士多德當時未提及第四格，第四格也僅僅是在第一格AAA、EAE式兩條公理下所能推理出的定理（郝旭東，2015）。本文采用包含第四格的三段論理論來論述，三段論的四個格及其對應的有效式如下：

第一格 第二格 第三格 第四格

M----P P----M M----P P----M

S----M S----M M----S M----S

S----P S----P S----P S----P

第一格的有效式為：AAA（核心公理），EAE（核心公理），AII（公理），EIO（公理），AAI，EAO

第二格的有效式為：AEE，EAE，AOO，EIO，AEO，EAO

第三格的有效式為：AAI，EAO，AII，EIO，IAI，OAO

第四格的有效式為：AAI，EAO，AEE，EIO，IAI，AEO

2 顯示法的運用

亞里士多德在《前分析篇》中提及可以運用顯示法證明的為第三格的AAI和OAO的證明。我運用了命題邏輯的方法對這兩例的具體如何運用顯示法證明進行了說明。

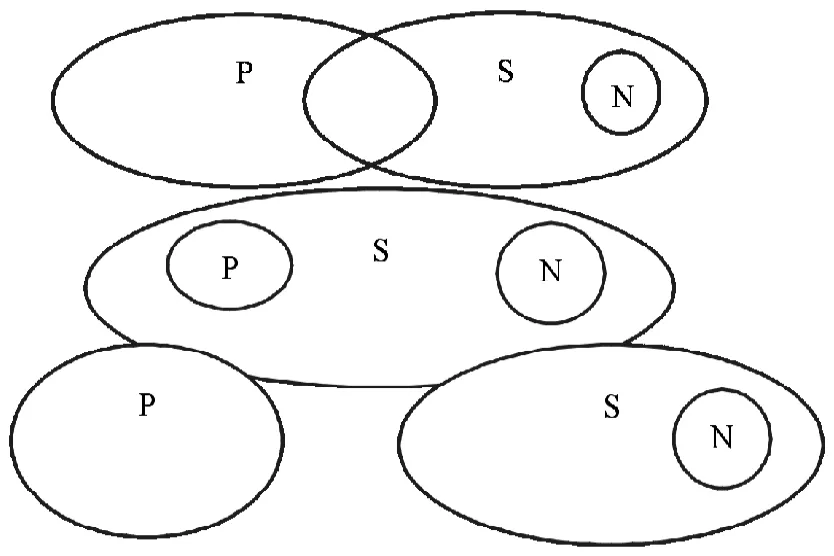
圖1 SOP表示的P、S、N的關系圖

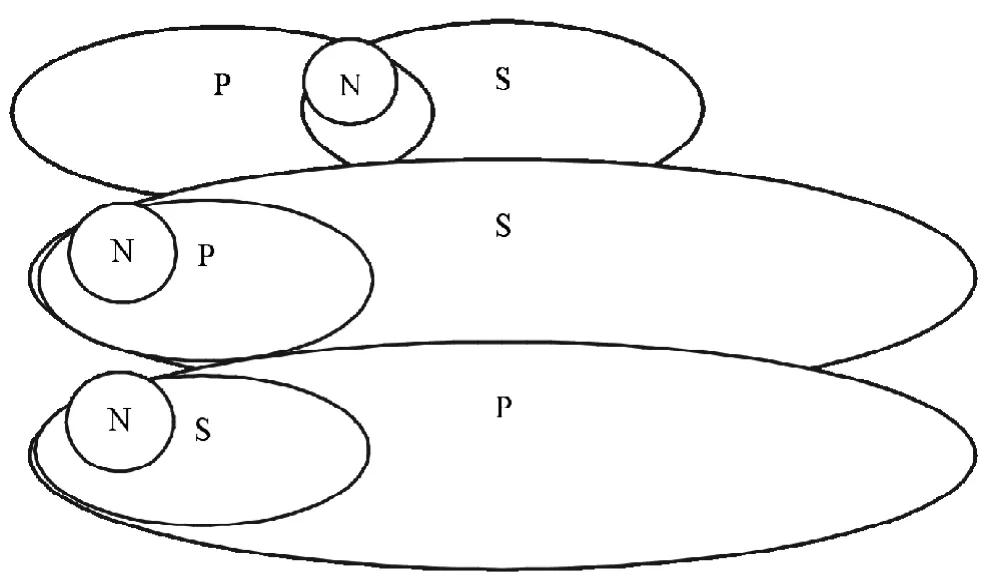
圖2 0SIP關系圖

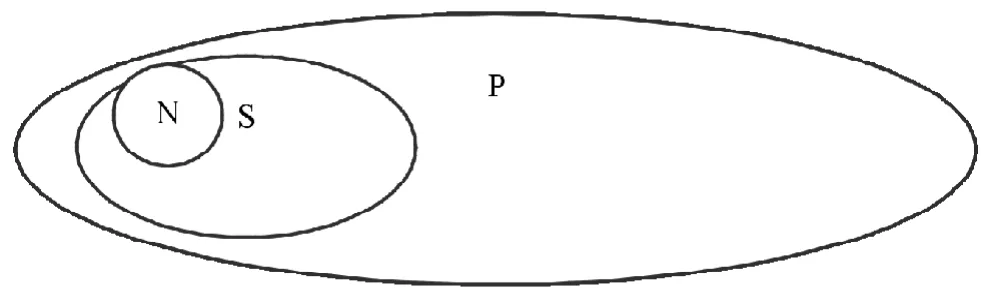
圖3 SAP關系圖

2.1 運用顯示法證明第三格AAI

（2）選取顯示詞項N，從S中選出N，N滿足所有N是P，所有N是R

（3）所以有SAP→NAP，SAR→NAR

（4）通過換位法NAR→RIN

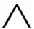
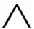
2.2 運用顯示法證明第三格OAO

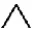
（2）選取顯示詞項N，從S中選出N，使N滿足所有N不是P。

（3）所以有SOP→NEP，SAR→NAR

（4）通過換位法NAR→RIN

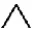
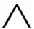
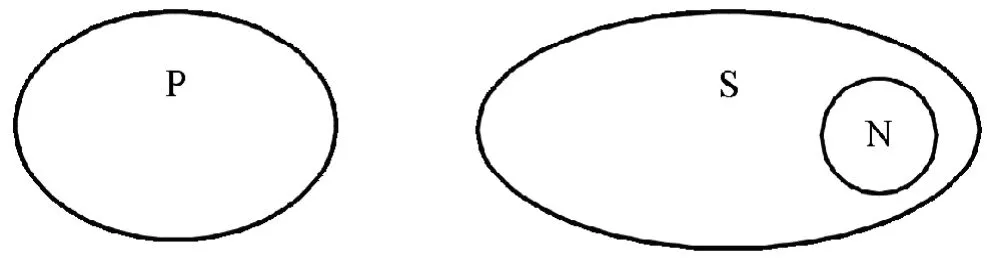
圖4 SEP關系圖

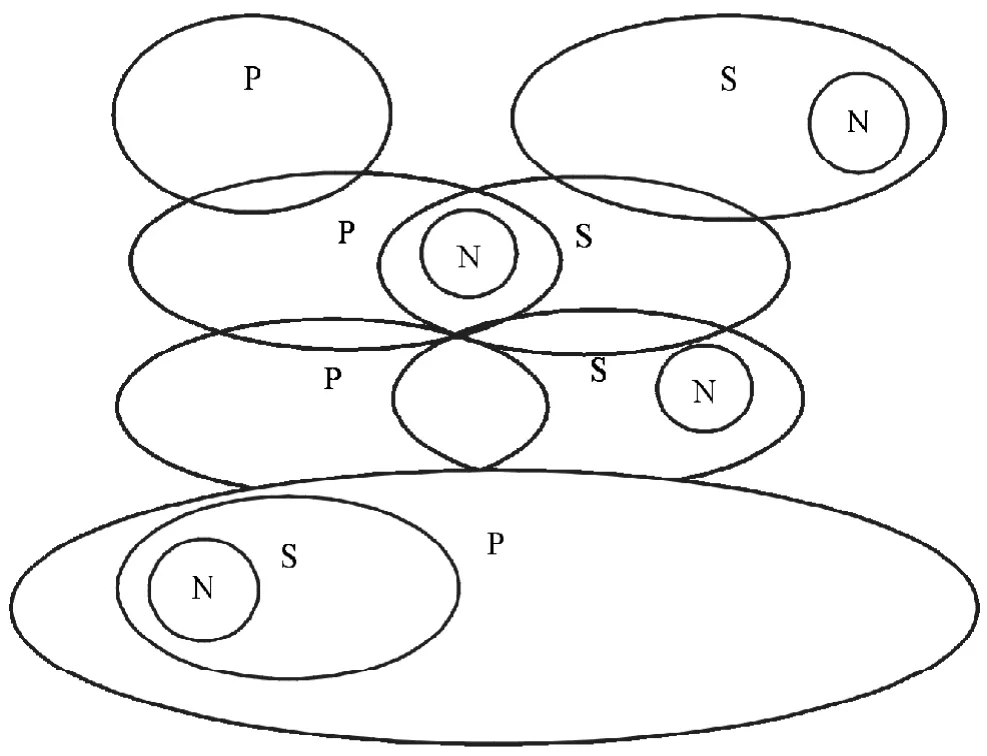
圖5 POS關系圖

第一個證明的意義不大，只是運用了顯示法，但核心的思路還是與亞里士多德書中給出的化歸法證明方式相同。第二個證明凸顯出了顯示法的作用，它與亞里士多德給出的歸謬的方法是完全不同的思路。

3 顯示法的原理及運用條件

顯示法在三段論的證明體系中，本質也是化歸的方法，更像是一種與換位法類似的證明途徑，為了更好的將要證明的式化歸為第一格的四條公理。顯示法的核心是選取適宜的顯示詞項，顯示詞項在原詞項范圍中，將原詞項的范圍縮小，從而可以具有更加明顯地與其他詞項的關系。

例如，在證明2中，從S中選出N，N滿足所有N不是P，因為原式含義是有的S不是P，用歐拉圖表示P、S、N的關系如圖1。

SOP所表示的P與S的關系共包含以上三種可能，在這三種可能下均可以選出顯示詞項N滿足所有N不是P的。所以有SOP→NEP。

為了運用顯示法證明其他各式的有效式，需要總結出各類三段論命題運用顯示法后所能得出的結果。

（1）0SOP：SOP表示有的S不是P。如上所述SOP→NEP。同時，在上圖所述的三種情況下，也可使選出的N滿足有的N不是P，即SOP→NOP。

（2）0SIP：SIP表示有的S是P，從S中選出N，使N滿足所有N是P，用歐拉圖表示三者的關系如圖2。

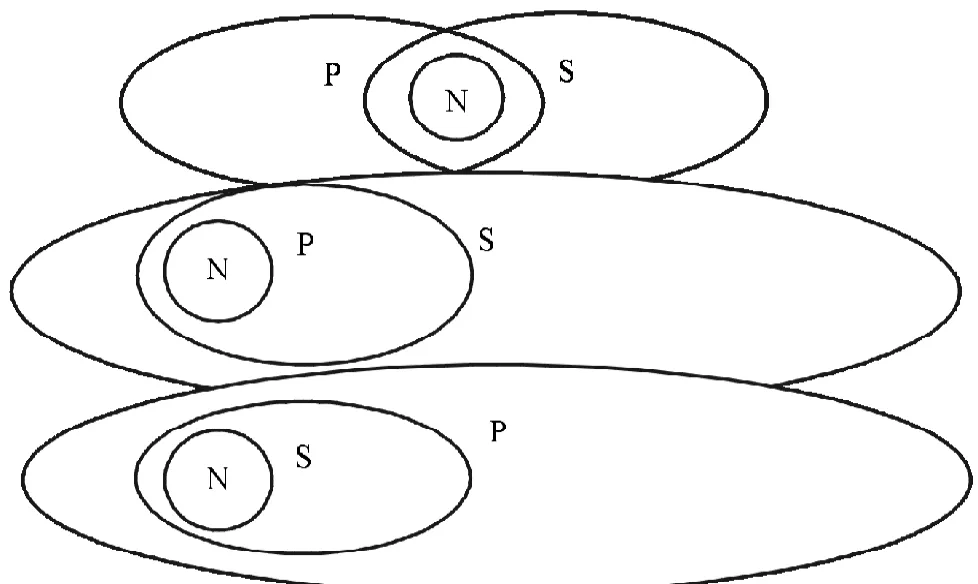
圖6 PIS關系圖

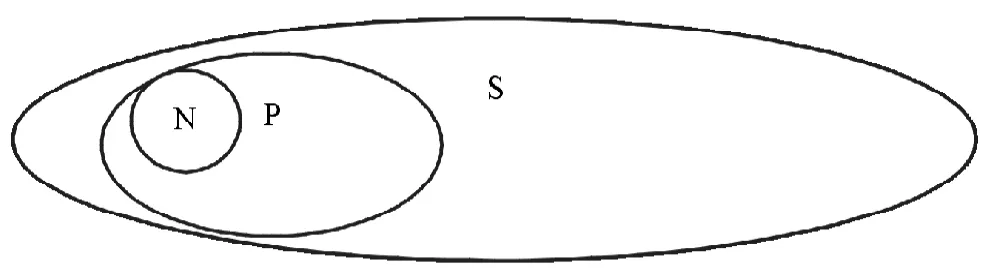
圖7 PAS關系圖

在SIP所包含的S與P的三種可能情況下，均可以選出N滿足所有N是P，所以有SIP→NAP

同時，在上圖中，也可以使N均滿足有的N是P，所以SIP→NIP。

（3）SAP：SAP表示所有S是P，從S中選出N，用歐拉圖表示所有可能的情況如圖3所示。

從圖中可以看出，無論N如何選擇，N均滿足所有N是P，所以SAP→NAP。

（4）SEP：SEP表示所有S不是P，從S中選出N，用歐拉圖表示三者可能的情況如圖4。

從圖中可以看出無論N如何選擇，均滿足所有N不是P，所以有SEP→NEP。

（5）POS：POS表示有的P不是S，從S中選出N，用歐拉圖表示三者之間關系如圖5所示。

無論N如何選擇，均滿足有的P不是N，所以POS→PON。

（6）PIS：PIS表示有的P是S，從S中選出N，使N滿足有的P是N，用歐拉圖表示P、S、從S中選出的顯示詞項N這三者之間的關系如圖6。

在P和S這三種關系的情況下，可以使N滿足有的P是N，所以有PIS→PIN。

（7）PAS：PAS表示所有P是S，從S中選出顯示詞項N，使N滿足有的P是N，如圖7所示。

所以可以選出符合條件的N，所以PAS→PIN。

同時也可以使N滿足所有P是N，如圖8。

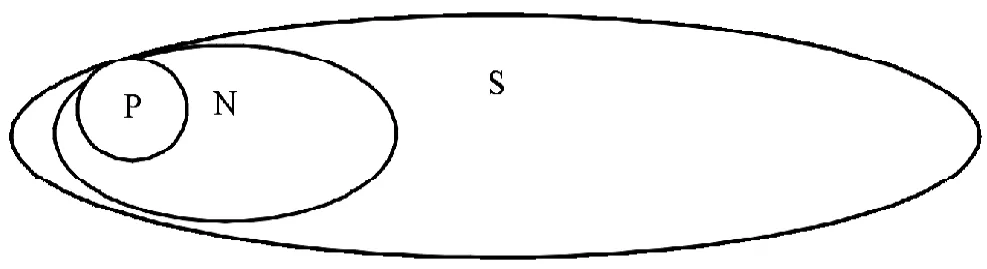
圖8 PIN關系圖

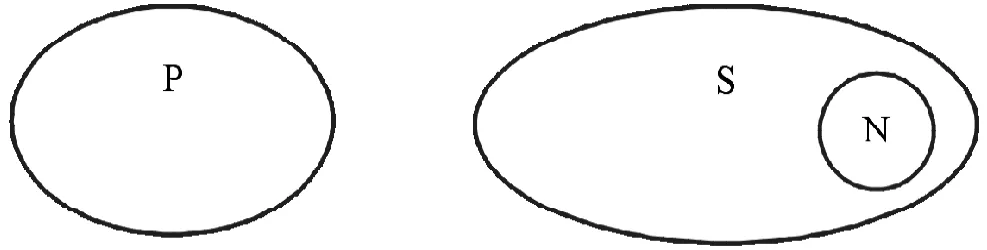
圖9 PES關系圖

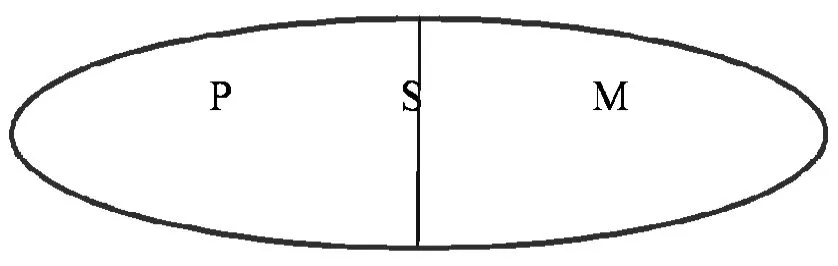
圖10 弱顯示式

所以可以選出符合條件的N，所以PAS→PAN。

（8）PES：PES表示所有P不是S，從S中選擇出顯示詞項N，這三者之間的關系如圖9所示。

根據圖像可以看出，無論N如何選擇，均有PES→PEN。

這8類三段論命題運用顯示法所能得到的蘊含式有：SOP→NEP、SOP→NOP、SIP→NAP、SIP→NIP、SAP→NAP、SEP→NEP、POS→PON、PIS→PIN、PAS→PIN、PAS→PAN、PES→PEN這11個。

其中，SAP→NAP、SEP→NEP、POS→PON、PES→PEN這四個蘊含式是無論N在S中如何選擇均成立的，我先將其定義為“強顯示式”。

另外，SOP→NEP、SOP→NOP、SIP→NAP、SIP→NIP、PIS→PIN、PAS→PIN、PAS→PAN這七個蘊含式是在不同的P與S的關系情況下選擇符合條件的N成立的，我將其定義為“弱顯示式”。

在第二部分的第一個例子中SAP→NAP，SAR→NAR這兩個是強顯示式，本質與換位法證明沒有區別。第二個例子中SOP→NEP是弱顯示式，SAR→NAR是強顯示式，在這個例子中顯示法的證明是一種與書中的歸謬法完全不同的證明方法。從這兩個例子可以看出，有實際應用價值的證明方法是第二個例子。第二個證明之所以有價值，主要是因為SOP→NEP這個弱顯示式的應用。而第一個證明沒有太多證明的實際意義主要是因為SAP→NAP，SAR→NAR這兩個式子只是把前提中的S替換成了N，命題類別沒有變化，向三段論第一格四條公理的化歸沒有幫助。所以，真正使顯示法有實際價值的是SOP→NEP、SIP→NAP、PAS→PIN這三個改變命題形式的弱顯示式。

但是，需要注意的是運用顯示法進行證明時，不能兩個蘊涵式都是弱顯示式。這是因為涉及四個詞項時，選出的顯示詞項不一定能同時保證滿足兩個條件。例如：SOP→NEP、SOM→NOM這兩式都是弱顯示式，如圖10所示。

S是P和M的總體，在這種情況下，從S中選擇的顯示詞項N，若滿足NEP就不能滿足NOM，若滿足NOM就不能滿足NEP。

4 顯示法的擴展應用

在清楚顯示法的應用原理以及適用的條件之后，具體的將顯示法應用于三段論的其他一些亞里士多德沒有提及可以用顯示法證明的有效式。

4.1 第一格AAI式

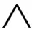
（2）從S中選出顯示詞項N，使N滿足有的R是N

（3）有SAP→NAP（強顯示式）、RAS→RIN（弱顯示式）

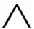
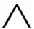
4.2 第一格EAO式

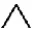
（2）從S中選出顯示詞項N，使N滿足有的R是N

（3）有SEP→NEP（強顯示式）、RAS→RIN（弱顯示式）

4.3 第二格EAO式

（2）從S中選出顯示詞項N，使N滿足有的R是N

（3）所以有PES→PEN（強顯示式）、RAS→RIN（弱顯示式）

（4）PEN→NEP（換位法）

4.4 第四格AAI式

（2）從S中選出顯示詞項N，使N滿足有的P是N

（3）所以PAS→PIN（弱顯示式）、SAR→NAR（強顯示式）

（4）RIP→PIR且PIR→RIP（換位法）

以上四個式是顯示法的典型運用，其實在三段論系統中的其他很多式也可以使用顯示法證明的。但是其他式就形似于第三格AAI式的證明，顯示法不是證明中的關鍵方法。從上文可以看出，三段論的有效式中有大部分都可以運用顯示法進行證明，其中有五個式（第三格OAO式加以上四個式）是顯示法的典型證明。所以，顯示法在三段論證明系統中并不是一個不重要的方法，而是因為化歸法和歸謬法的廣泛運用而被忽視的重要方法。