基于BP神經網絡預測林內PM2.5濃度

陳博 李迎春 夏振平

摘要[目的]利用BP神經網絡預測林內PM2.5濃度。[方法]利用人工神經網絡理論，采用2013年7月—2014年5月野外實時監測數據，建立了以氣象參數、污染源強變量和林分結構特征為輸入因子，林內PM2.5小時平均濃度為輸出因子的預測模型，并對其預測精度進行了評價。[結果]BP人工神經網絡模型能夠很好地捕捉污染物濃度與氣象因素和林分結構間的非線性影響規律，預測結果的平均相對誤差為1.71×10-3，均方根誤差為6.77，擬合優度達0.98，模型具有很高的預測精度。而傳統的多元線性回歸（MLR）模型預測結果的平均相對誤差、均方根誤差和擬合優度分別為0.27、22.92和0.93。[結論]研究成果印證了應用BP人工神經網絡模型預測林內PM2.5濃度的可行性和準確性。

關鍵詞PM2.5;BP人工神經網絡;多元線性回歸;林分結構

中圖分類號S771.8文獻標識碼A

文章編號0517-6611（2019）01-0107-04

doi：10.3969/j.issn.0517-6611.2019.01.033

開放科學（資源服務）標識碼（OSID）：

PM2.5指大氣中直徑小于或等于2.5μm的顆粒物，常被稱為可入肺顆粒物或細顆粒物[1]。雖然PM2.5只是大氣成分中含量很少的組分，但其在空氣中的重力沉降率幾乎為零，長期在空氣中懸浮，附著很多有機污染物和重金屬元素[2]，對人類健康、環境和氣候有重要影響。植物作為環境綠化的主體，對空氣有一定的凈化作用，森林植被可以通過直接和間接的方式對大氣中顆粒物的濃度產生影響[3-6]。然而森林植被對PM2.5的作用研究尚處于起步階段，林內PM2.5濃度變化規律及林內外濃度對比情況尚不清楚。已有文獻報道林內PM2.5的質量濃度受污染散發源、氣象條件和林分結構等多種因素影響[7-10]，既存在林內PM2.5濃度低于林外，也存在林內PM2.5濃度高于林外的情況。鑒于此，準確預測林內PM2.5濃度對于研究森林調控PM2.5的作用效果及引導公眾健康出游、親近森林具有重要意義。

研究表明，PM2.5濃度的變化與氣象條件之間呈很強的非線性關系[11]，傳統的多元線性回歸模型預測PM2.5質量濃度存在很大局限性。然而人工神經網絡能夠建立非常復雜的非線性模型，很好地反映PM2.5質量濃度與參數之間的關系[12-13]，此種方法已經成功地用于多種污染物的預測研究[14-15]。筆者以北京市大興區黃村鎮景觀生態林為研究對象，應用BP人工神經網絡模型預測林內PM2.5小時平均質量濃度，并與多元線性回歸預測結果做比較，說明基于人工神經網絡模型預測林內PM2.5質量濃度的可行性和準確性。

1實驗方法原理

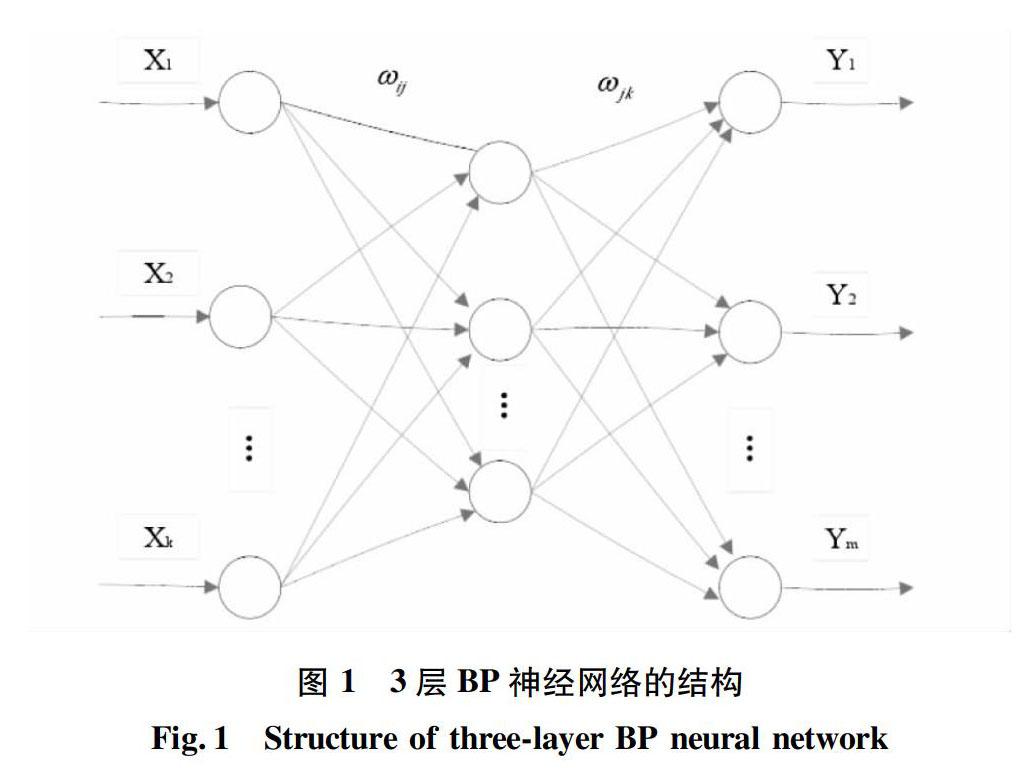
BP神經網絡屬于多層前饋神經網絡，據統計，有80%～90%的神經網絡模型采用了BP網絡或它的變化形式[16]。BP神經網絡的構成包括1個輸入層、1個或多個隱藏層以及1個輸出層，主要特點為信號前向傳遞，而誤差反向傳播。BP算法的原理是在前向的傳遞中，信號經由輸入層、隱含層和輸出層的逐層處理及傳遞，如果預測輸出和給定輸出之間的誤差未達到精度要求，則轉為反向傳播并修正連接權值，進而促使預測輸出逐漸逼近期望輸出。3層BP神經網絡的結構如圖1所示。一般采用S型的轉換函數作為傳遞輸入層與隱含層之間關系的函數，采用純線性的轉換函數作為傳遞隱含層與輸出層之間關系的函數[17]。BP人工神經網絡輸入層和隱含層間的S型傳遞函數表達公式如下：

F（x）=1/（1+e-x）（1）

式中，x表示輸入該神經元，將神經元（-∞，+∞）的輸入范圍映射到（0，+1）較小的范圍內，便于BP算法訓練神經網絡。

2實驗設計

2.1數據獲取該研究中采用的283組數據由野外實時監測得到。2013年7月—2014年5月，每個季度隨機抽取無降水天氣9d，每天連續監測9h。在北京市大興區黃村鎮大洼村景觀生態林林內監測點和林外2個監測點同步監測1.5m高處空氣中的PM2.5濃度及氣象要素（溫度、相對濕度、風速、風向），為了保證監測點具有相近的污染源，且避免監測點出現林緣效應，林內監測點設在景觀生態林中心位置，距林緣50m，林外監測點設在林外距林緣50m的位置且四周空曠無高大喬木和建筑遮擋。林內樣地主要喬木為旱柳（Salixmatsudana），平均樹高6m、平均胸徑12cm，林緣伴生榆葉梅（Prunustriloba）和碧桃（Prunuspersica）等少量的花灌木。

采用英國Turnkey儀器制造公司生產、符合粉塵監測國家標準的Dustmate粉塵檢測儀（分辨率0.1μg/m3，測量范圍0～6000μg/m3，粒徑范圍0.5～15.0μm）測定PM2.5濃度，使用臺灣衡欣az8918風速氣溫濕度三合一測試儀及TNF三杯式風速表測定氣溫、相對濕度、風速和風向等。

2.2數據處理由于大氣污染物的濃度變化受氣象條件的影響，因此要實現對林內PM2.5質量濃度的預測，必須同時考慮林外PM2.5背景值及林內氣象條件。

（1）背景濃度：將林外監測點的PM2.5濃度設為預測模型輸入參數中的背景濃度，即用PM表征污染源強對林內PM2.5濃度的影響。

（2）氣象參數：選取溫度（T）、相對濕度（H）和風速（VW）數據為氣象參數直接進入分析。風向（θ）經由正弦和余弦轉換成2個變量sinθ和cosθ[17]，即把風向轉換成為東西方向和南北方向2個變量。

（3）季節參數：考慮一年中不同季節植物生長快慢不同對林內PM2.5濃度變化產生不同影響，引進季節變量Aseason作為雙變量使用。根據旱柳生長習性，春季和夏季生長旺盛，令Aseason=0;秋季和冬季生長緩慢，令Aseason=1。

建立的預測模型中全部的輸入變量如表1所示。

2.3BP人工神經網絡模型基于BP人工神經網絡方法仿真林內PM2.5濃度的過程主要由MatlabR2013a中神經網絡工具箱所提供的函數開展編程并建立起相應的模型而實現。具體網絡實現步驟如下：Step1，網絡初始化。將輸入層到隱含層以及隱含層到輸出層所有的權值設置成任意小的隨機數，并設定初始閾值。Step2，讀入輸入變量與輸出變量（林內PM2.5質量濃度）。全部樣本數據被隨機分成訓練組和測試組：訓練組樣本占70%用于訓練網絡，根據顯示的誤差調試網絡，其中訓練法則為Levenberg-Marquardt運算法則;測試組樣本占30%用于獨立測試訓練網絡的性能，結果對訓練過程無影響。Step3，選擇訓練函數，在設置隱藏層神經元的數目后訓練網絡。當網絡不能收斂時，則需要更換訓練函數;當結果誤差比較大時，則需要將隱藏層神經元的數目進行調整，之后再次訓練網絡，如此反復訓練，最終獲得最佳訓練結果。Step4，確定BP神經網絡的最終結構：單隱層，各層神經元數目為7-6-1，訓練函數確定為trainlm，并使用訓練好的網絡對林內PM2.5小時平均濃度進行仿真。

2.4多元線性回歸模型將多元線性回歸（multiplelinearregression，MLR）模型與人工神經網絡模型相比較，其中MLR模型是通過MatlabR2013a所建立。MLR模型的數學表達式如下：

Y=b0+ni=1biXi+εi（2）

式中，Xi表示輸入變量i的值;Y表示林內PM2.5質量濃度實測值;用最小二乘法計算求得常數項b0及回歸系數bi;εi是回歸誤差，回歸求解的過程就是使平均誤差最小的過程。

通過逐步（stepwise）回歸法將該研究全部的輸入變量進行篩選，得到林內PM2.5質量濃度ρ（PM2.5）的多元線性回歸預測模型如下：

ρ（PM2.5）=-19.2179+0.9689ρ（PM02.5）+0.0946H+0.3425VW-0.4583T

預測模型顯示，預測林內PM2.5濃度時背景濃度的影響非常重要，其次是相對濕度。該預測模型經過逐步回歸法后留取了4個輸入變量（背景濃度、相對濕度、風速和溫度），風向變量和季節變量未能進入回歸。

47卷1期陳博等基于BP神經網絡預測林內PM2.5濃度

3結果與分析

3.1監測數據統計學描述在預測模型輸入變量中，由于背景濃度（林外PM2.5濃度）對林內PM2.5濃度的預測結果影響最為重要，故將背景濃度數據與林內PM2.5濃度數據分別描述，并進行T檢驗，以了解林內和林外PM2.5濃度數據本身的差異，避免因對比數據無顯著差異而不適合采用以上模型進行預測。由表2可知，林外PM2.5濃度最小值高于林內，最大值低于林內，PM2.5小時平均濃度為林外高于林內;T檢驗統計量觀測值對應的雙尾概率P值接近0，如果設定顯著水平α為0.05，則P值小于α，可認為林內和林外PM2.5濃度存在顯著差異。

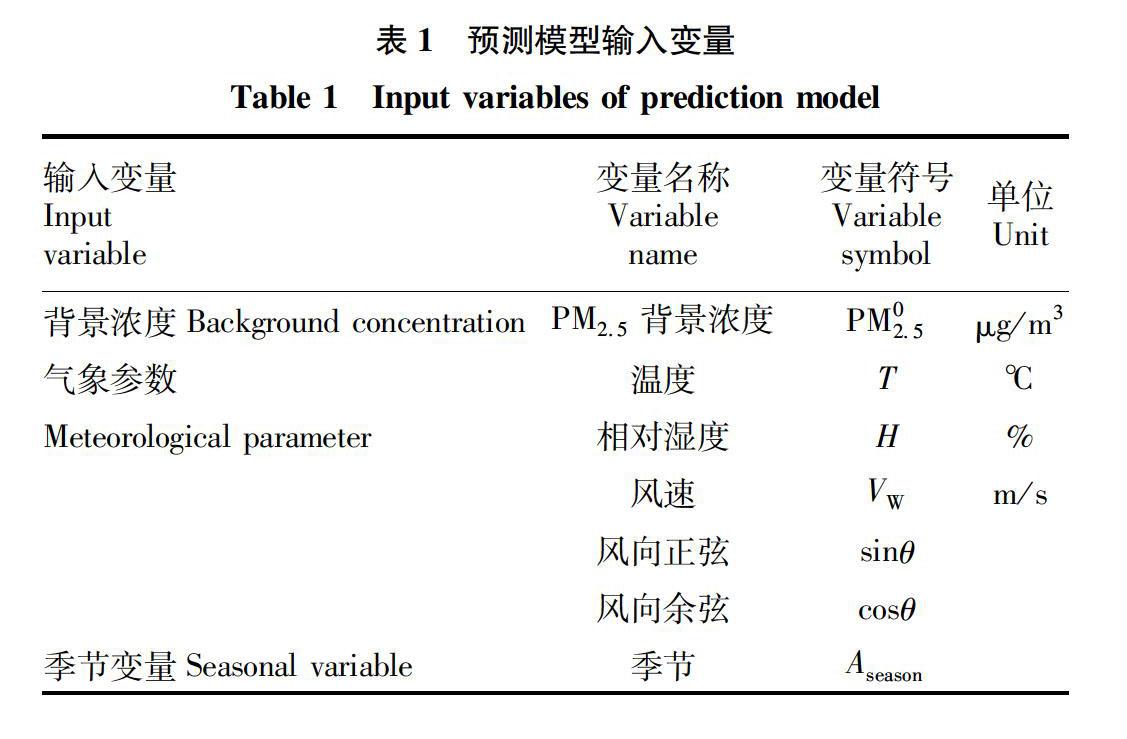
3.2預測結果比較圖2是基于BP人工神經網絡方法和MLR方法仿真生成的研究區林內PM2.5濃度的預測值與觀

測值的比對。圖2顯示BP人工神經網絡模型與MLR模型

預測結果之間存在明顯的差異。BP人工神經網絡模型比較好地預測了不同天氣情況下林內PM2.5的質量濃度變化，盡管對于數據急劇變化（突然增大或減小）的點，神經網絡的預測誤差相較于平滑變化的點略微增大，但是整體的預測曲線非常接近實測曲線。而MLR模型的預測效果明顯不及BP人工神經網絡模型的預測效果。從圖2可以看出，當大氣中PM2.5濃度較高（>100μg/m3）時，MLR模型的預測結果明顯高于實際觀測值;當大氣中PM2.5濃度較低（<10μg/m3）時，預測結果明顯低于實際觀測值，甚至出現負值（見紅框所示），說明采用MLR模型預測林內PM2.5濃度時存在一定局限性和不確定因素。為了更好地體現以上2種模型的預測能力，該研究采用預測精度對模型進行評價。

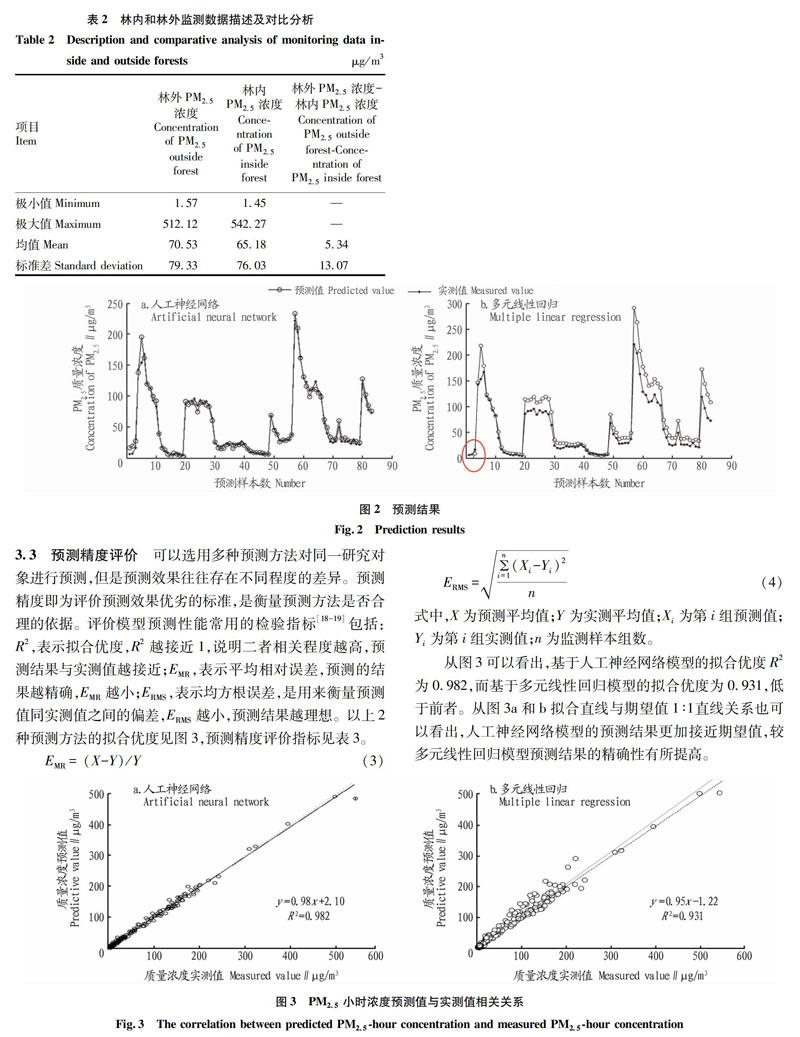
3.3預測精度評價可以選用多種預測方法對同一研究對象進行預測，但是預測效果往往存在不同程度的差異。預測精度即為評價預測效果優劣的標準，是衡量預測方法是否合理的依據。評價模型預測性能常用的檢驗指標[18-19]包括：R2，表示擬合優度，R2越接近1，說明二者相關程度越高，預測結果與實測值越接近;EMR，表示平均相對誤差，預測的結果越精確，EMR越小;ERMS，表示均方根誤差，是用來衡量預測值同實測值之間的偏差，ERMS越小，預測結果越理想。以上2種預測方法的擬合優度見圖3，預測精度評價指標見表3。

EMR=（X-Y）/Y（3）

ERMS=ni=1（Xi-Yi）2n（4）

式中，X為預測平均值;Y為實測平均值;Xi為第i組預測值;Yi為第i組實測值;n為監測樣本組數。

從圖3可以看出，基于人工神經網絡模型的擬合優度R2為0.982，而基于多元線性回歸模型的擬合優度為0.931，低于前者。從圖3a和b擬合直線與期望值1∶1直線關系也可以看出，人工神經網絡模型的預測結果更加接近期望值，較多元線性回歸模型預測結果的精確性有所提高。

由表3可知，用神經網絡預測的平均相對誤差EMR為1.71×10-3、均方根誤差ERMS為6.77;而MLR模型預測的平均相對誤差EMR為0.27、均方根誤差ERMS為22.92。雖然2種方法得到的預測值與實測值的相關性都很高（圖3），但從誤差值大小可以看出，BP神經網絡模型預測的誤差值遠小于MLR模型。表3對比了2種模型預測精度，結果表明神經網絡具有很強的穩定性和容錯性[19]，綜合信息能力強，能夠很好地處理復雜的非線性關系。以上分析說明2種預測模型均能預測林內PM2.5濃度的小時平均值，相較而言，采用人工神經網絡模型對林內PM2.5濃度值變化的預測結果比通過多元線性回歸模型的預測結果更加接近實際觀測值的變化。

4小結

（1）BP人工神經網絡和傳統多元線性回歸模型2種方法均可以用于林內大氣PM2.5質量濃度預測，盡管二者在PM2.5濃度急劇變化時預測存在一定缺陷，但仍然能夠在稀疏監測數據輸入條件下基本反映林內PM2.5污染的時間變化規律。

（2）相對于多元線性回歸模型，BP人工神經網絡具有很強的自學習、自組織與自適應功能，可以更加準確地實現林內PM2.5質量濃度小時平均值的預測，其預測結果能更好地捕捉氣象因素對大氣污染物濃度的非線性影響規律。BP人工神經網絡能夠成為預測林內PM2.5質量濃度的較優方法。

（3）文中所選的污染源強表征變量和氣象參數數據容易獲得，且可以比較準確地反映氣象變化和林分作用對PM2.5質量濃度的影響，是預測林內PM2.5質量濃度較為理想的輸入變量。

（4）采用人工神經網絡方法建立的林內PM2.5質量濃度預測模型適用于不同大氣污染程度，但是在一般污染濃度情況下對林內PM2.5濃度的預測效果比高污染時期的預測效果更為準確。

參考文獻

[1]邵龍義，時宗波，黃勤.都市大氣環境中可吸入顆粒物的研究[J].環境保護，2000（1）：24-26，29.

[2]孫淑萍，古潤澤，張晶.北京城區不同綠化覆蓋率和綠地類型與空氣中可吸入顆粒物（PM10）[J].中國園林，2004，20（3）：77-79.

[3]YUY，SCHLEICHERN，NORRAS，etal.DynamicsandoriginofPM2.5duringathree-yearsamplingperiodinBeijing，China[J].Journalofenvironmentalmonitoring，2011，13（2）：334-346.

[4]吳海龍，余新曉，師忱，等.PM2.5特征及森林植被對其調控研究進展[J].中國水土保持科學，2012，10（6）：116-122.

[5]BECKETTKP，FREERSMITHPH，TAYLORG.Particulatepollutioncapturebyurbantrees：Effectofspeciesandwindspeed[J].Globalchangebiology，2000，6（8）：995-1003.

[6]LANGNERM.Reductionofairborneparticulatesbyurbangreen[J].Bundesamtfürnaturschutz，2008，179：129-137.

[7]CAVANAGHJAE，ZAWAR-REZAP，WILSONJG.Spatialattenuationofambientparticulatematterairpollutionwithinanurbanisednativeforestpatch[J].Urbanforestry&urbangreening，2009，8（1）：21-30.

[8]郭二果，王成，郄光發，等.北京西山典型游憩林空氣懸浮顆粒物季節變化規律[J].東北林業大學學報，2010，38（10）：55-57.

[9]殷杉，蔡靜萍，陳麗萍，等.交通綠化帶植物配置對空氣顆粒物的凈化效益[J].生態學報，2007，27（11）：4590-4595.

[10]汪永英，孫琪，李昭，等.典型天氣條件下哈爾濱城市森林不同林型對PM2.5的調控作用研究[J].安徽農業科學，2016，44（5）：175-179.

[11]GARDNERMW，DORLINGSR.Statisticalsurfaceozonemodels：Animprovedmethodologytoaccountfornonlinearbehaviour[J].Atmosphericenvironment，2000，34（1）：21-34.

[12]CHALOULAKOUA，SAISANAM，SPYRELLISN.ComparativeassessmentofneuralnetworksandregressionmodelsforforecastingsummertimeozoneinAthens[J].Scienceofthetotalenvironment，2003，313（1/2/3）：1-13.

[13]MCKENDRYIG.Evaluationofartificialneuralnetworksforfineparticulatepollution（PM10andPM2.5）forecasting[J].Journaloftheair&wastemanagementassociation，2002，52（9）：1096-1101.

[14]KOLEHMAINENM，MARTIKAINENH，RUUSKANENJ.Neuralnetworksandperiodiccomponentsusedinairqualityforecasting[J].Atmosphericenvironment，2001，35（5）：815-825.

[15]PAPANASTASIOUDK，MELASD，KIOUTSIOUKISI.DevelopmentandassessmentofapplicationofneuralnetworkandmultipleregressionmodelsinordertopredictPM10levelsinamediumsizedMediterraneancity[J].Water，air&soilpollution，2007，182：325-334.

[16]曹虹.基于BP神經網絡的交通流量預測[D].西安：長安大學，2012：30.

[17]王敏，鄒濱，郭宇，等.基于BP人工神經網絡的城市PM2.5濃度空間預測[J].環境污染與防治，2013，35（9）：63-70.

[18]石靈芝，鄧啟紅，路嬋，等.基于BP人工神經網絡的大氣顆粒物PM10質量濃度預測[J].中南大學學報（自然科學版），2012，43（5）：1969-1974.

[19]宰松梅，郭冬冬，韓啟彪，等.基于人工神經網絡理論的土壤水分預測研究[J].中國農學通報，2011，27（8）：280-283.