電子設備封閉腔內自然對流冷卻效果數值分析

王 燁，趙興杰，藺虎相，宋榮飛，管國祥

?

電子設備封閉腔內自然對流冷卻效果數值分析

王 燁1,2，趙興杰1，藺虎相1，宋榮飛1，管國祥1

（1. 蘭州交通大學環境與市政工程學院，蘭州 730070；2. 蘭州交通大學鐵道車輛熱工教育部重點實驗室，蘭州 730070）

為了研究安裝于封閉空間內的電子設備散熱元件屬性及空間位置對腔內自然對流傳熱特性的影響，該文采用FLUENT14.5軟件中的RNG-湍流模型對流體為空氣、高寬比為1的封閉腔內溫度場、流場、壁面傳熱能力進行了數值分析。結果表明：在熱壁面1/3高度處布置1個導熱翅片時熱壁面的平均數比相同位置布置絕熱翅片時提高了9.67%；在熱壁面1/3高度處、冷壁面2/3高度處同時各布置1個導熱翅片時熱壁面平均數可取得雙翅片工況的最大值39.94，比單翅片的最優工況平均數提高了14.34%。本文研究結果對于改善工農業工程中電子元器件的自然對流冷卻效果、優化散熱元器件的空間布置具有一定的理論指導意義。

數值模擬；溫度；對流換熱；封閉腔；翅片

0 引 言

封閉腔內的自然對流現象廣泛存在于諸多工業生產系統中，比如太陽能集熱器系統、電子設備的冷卻、建筑熱工設計、核反應堆設計等。在農業大棚內發生的自然對流熱質交換過程對于室內溫濕度、氣流速度的控制與產品數量及質量密切相關。因此，對封閉空間內自然對流機理的研究對于改善這些系統的綜合性能具有重要的工程實際意義。ButChelor[1]以雙層窗為研究對象，首次探討了不同瑞利數下雙層窗玻璃夾層中的自然對流換熱機理。后來人們又從腔體高寬比[2]、瑞利數[3-8]、普朗特數[8-10]、腔體傾角[11]等方面進行了卓有成效的探索。

在強化封閉腔內自然對流傳熱措施方面，有在腔內側壁面施加正弦變壁溫條件[12]，或在腔內設置一個旋轉圓柱體[13]以及在腔體內側壁上布置水平薄翅片等[14]。Ampofo[15]用實驗方法揭示了內置翅片對封閉腔內自然對流傳熱特性的影響機理，發現內置翅片強化了熱壁面的傳熱能力，冷壁面邊界層上的速度場、溫度場及湍流參量的峰值均有了顯著提高。目前，內置翅片對封閉腔內自然對流傳熱特性的影響研究重點主要涉及翅片長度[16-19]、翅片傾斜角[19]、翅片形狀[20-21]、翅片材質[22-25]等方面。

關于翅片材質對封閉腔內傳熱特性的研究比較一致的結論是：封閉腔內傳熱效率隨翅片導熱系數增大而增大。而Nag等[22]的研究發現：在豎向熱壁面上布置的導熱翅片對冷壁面的傳熱有強化作用，在熱壁面上布置的絕熱翅片反而弱化了冷壁面的傳熱。Frederick等[23]對于有內置翅片的封閉腔內自然對流換熱三維數值研究表明：位于豎向熱壁面上的翅片導熱性越好，翅片的阻擋作用越弱，對腔內的傳熱強化效果越顯著。Xu等[24]對比研究了封閉腔內湍流自然對流中側壁所布置單一導熱翅片和絕熱翅片對流場結構和傳熱效率的影響，但沒有給出翅片的優化配置方案。Elatar等[25]研究了封閉腔內層流狀態下位于側壁高溫面上的翅片導熱性對翅片效率和對流傳熱效率的提高程度，得到了不同翅片導熱率情況下壁面平均努塞爾特數與數和翅片高度之間的關系式。這類對于單一翅片的研究成果已廣泛應用于工業生產中[26-28]。但這些研究只是針對單一因素進行探討的，關于有內熱源情況下封閉腔內側壁翅片位置和數量對湍流自然對流傳熱特性共同影響的研究還未見報道。而不斷集成化的工業設備及系統優化設計中，在同一封閉空間里往往是多熱源、多元件并存的，如何合理布置這些發熱元件并控制封閉空間內的流動冷卻過程，對于系統的安全運行和可靠性非常重要。基于這樣的工程背景，本文針對有內熱源的封閉腔內側壁翅片屬性、數量、位置等因素對腔內自然對流冷卻的影響規律及溫度場與流場的耦合作用機理進行了研究，以獲得冷卻性能最優的最佳翅片數量和位置組合，從而為農業及工業工程中類似于封閉空間中電子元件的優化布置并提高其使用壽命提供理論參考。

1 封閉腔物理模型和數學模型

1.1 物理模型

本文所研究的封閉腔橫斷面結構如圖1所示。以文獻[29]的研究模型為例，寬、高、深分別取=0.75 m、=0.75 m、=1.5 m。

注：Th為熱壁面溫度，℃；Tc為冷壁面溫度，℃；H為腔體高度，m；L為腔體寬度，m；a為熱壁面上翅片與腔體底面之間的距離，m；b為冷壁面上翅片與腔體底面之間的距離，m；c為熱源頂面與腔體底面之間的距離，m。

根據文獻[29]，當封閉腔深寬比大于1.8時可以不考慮腔體內流動的三維效應。所以本文采用二維數值模擬。腔體內為空氣，流體密度變化采用Boussinesq假設，=1.58×109。

翅片高度均為80 mm，翅片厚度為4 mm。自然對流換熱中，流場與溫度場之間存在強烈的耦合關系，不同翅片位置組合會對封閉腔內流場和溫度場分析產生不同影響，從而影響自然對流換熱性能。為了揭示這一特性，本文設計了如表1所示的計算模型。定義無量綱長度：=/，=/，，分別為水平和鉛錘方向的實際距離，m；=0.75 m。

表1 物理模型的尺寸設置

1.2 控制方程數學模型

由于RNG模型在計算湍流動能耗散率方程中產生項系數時引入了主流的時均應變率，使得產生項系數既與流動情況有關，也是空間坐標的函數，從而有效地改善了計算精度；另一方面，RNG模型也考慮了湍流渦旋結構，而本文模型中氣流通過翅片的擾流會產生顯著的渦旋結構。因此，本文采用RNG模型更適合于準確捕捉翅片與側壁結合部位以及腔體內部其余位置形成的渦旋結構，從而能更準確地描述所研究腔體中的流動與傳熱過程。本文計算中常數項1ε=1.42，2ε=1.68。

1.3 邊界條件和初始條件

參考文獻[29]，熱壁面溫度為323.15 K，冷壁面溫度為283.15 K，熱源溫度為353.15 K。參考文獻[30]，頂面和底面向外散熱的熱流密度均為-7.0 w/m2，封閉腔內初始溫度取冷、熱壁面溫度的算術平均值，為303.15 K，所有氣固交界面為速度無滑移條件。

2 數值求解方法

2.1 數學模型驗證

為了保證數學模型以及數值方法的正確性，需要進行模型驗證。本文在=1.58×109條件下與Tian[29]的試驗數據進行比對。選擇表1中的物理模型1，網格數為260×260，時間步長為0.01 s，邊界條件與文獻[29]的相同。氣固交界面取速度無滑移條件。采用RNG-模型對封閉腔內空氣自然對流與傳熱過程進行數值模擬，得到腔體側壁距底面無量綱長度=0.5處水平線上的豎向速度值、溫度值與文獻[29]的試驗數據比對結果，如圖2所示。

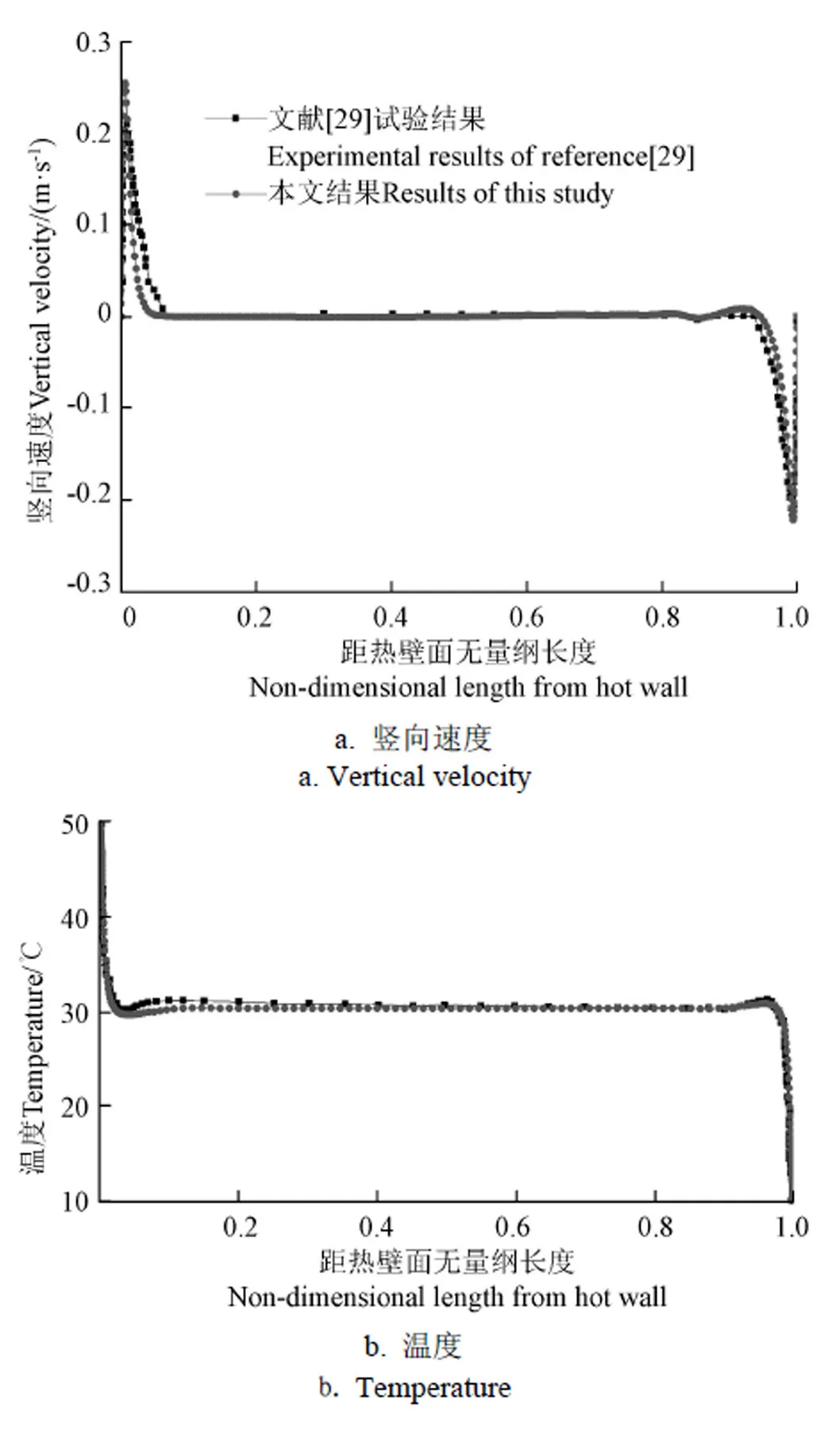
圖2 本文數值結果與文獻[29]試驗結果比對（距底面無量綱長度Y=0.5） Fig. 2 Comparisons between numerical results in this paper and experimental results in reference [29] (non-dimensional length from bottom Y=0.5)

本文模擬結果的速度值與文獻[29]試驗結果的相對誤差最大值為4.8%，最小值為0；本文模擬結果的溫度值與文獻[29]試驗結果的相對誤差最大值為3.2%，最小值為0。由于近壁區速度梯度和溫度梯度均很大，導致了較大的測試誤差，從而使得數值結果與試驗結果間存在較大的相對偏差，但速度及溫度的相對偏差值已經足以證明所采用數學模型的正確性和可靠性[10]。模型和數值方法可用于封閉腔內空氣湍流自然對流與傳熱特性的數值分析。

2.2 迭代時間步長

根據表1中的物理模型1，分別采用0.02、0.05和0.10 s的時間步長進行數值試驗，將3種時間步長得到的熱壁面距底面無量綱長度=0.5處水平線上的豎向速度及溫度分別進行對比。3種時間步長對速度的計算結果的最大相對偏差為0.09%，最小相對偏差為0。3種時間步長對溫度的計算結果的最大相對偏差為0.02%，最小相對偏差為0。不同時間步長計算結果的差異滿足工程計算精度要求[10]，在保證計算精度的前提下，為了節約計算時間并確保后續工況計算收斂，本文選取時間步長為0.05 s。

2.3 網格獨立性驗證

對于只在熱壁面上布置1個翅片的情況，選取翅片位于熱壁面距底面以上1/6高度處的物理模型，在相同邊界條件下，采用3套網格（41 358、69 154、98 124）進行試算，3套網格所得=0.5處外法線上的豎向速度最大相對偏差為0.03%、最小相對偏差為0；溫度最大相對偏差為0.01%、最小相對偏差為0。在保證計算精度的前提下[10]，為了節約計算時間，本文選取69 154為后續計算的網格數。

對于在熱、冷壁面上同時布置翅片的情況，選取熱壁面翅片位于距底面以上1/3H處、冷壁面翅片位于距底面以上1/3H處的物理模型為計算模型，在相同邊界條件下，采用3套網格（45 725、68 067、90 822）進行試算，3套網格所得=0.5處外法線上的豎向速度最大相對偏差為0.8%、最小相對偏差為0；溫度最大相對偏差為0.4%、最小相對偏差為0。在保證計算精度的前提下[10]，確定計算網格數為68 067。

據此確定適合于本文研究表1中模型1的網格數為67 081，模型2～模型6的網格數為69 154，模型7和模型10的網格數為68 067，模型8和模型9的網格數為67 967。

2.4 求解計算

離散格式為：壓力項采用Green-Gauss Cell Based 格式離散[31]，動量方程、能量方程、湍流動能方程及湍流動能耗散率方程均采用二階迎風格式離散，采用SIMPLE算法求解速度和壓力耦合問題。松弛因子設置[31]：壓力為0.3，動量為0.7，湍流動能和湍流動能耗散率均為0.8，能量方程、湍流黏度、體積力和密度均為1。湍流模型選用RNG-模型。求解控制方程時的收斂條件與文獻[31]相同。

3 計算結果與分析

3.1 翅片材質對腔內對流和傳熱的影響

內置熱源的封閉腔內自然對流在房間空調冷卻、電力設備冷卻等方面應用廣泛，但翅片是否導熱對冷卻效果的影響不同。將翅片分別布置在熱壁面距底面以上1/6、1/3、1/2、2/3、5/6高度處，分析導熱和絕熱翅片位置與內置熱源對封閉腔內對流和傳熱的綜合影響。

絕熱翅片表面熱流密度為0。導熱翅片由于高度（沿壁面外法線方向的尺寸）小、導熱系數大（銅板=398 W/m·K），計算中近似認為其表面溫度均勻且和熱壁面溫度相同，為323.15 K，熱源除了底面絕熱外，其余各表面溫度均為353.15 K。

圖3為絕熱翅片位于熱壁面不同位置時沿熱壁面高度方向局部數的變化曲線。可以看出，在<0.1范圍內熱壁面局部數幾乎不受翅片位置影響。但隨著邊界層的不斷發展，局部數在翅片的下表面和上表面發生了階躍性變化，最大值達到了75，最小值接近0。這是因為翅片在側壁上起到了渦旋發生器的作用，浮升力作用下不斷上升的氣流首先遇到翅片發生滯止，隨即繞過翅片并在翅片上方形成渦旋，從而強化了翅片基部的傳熱過程。熱壁面局部數沿流動方向因溫度梯度逐漸減小而呈下降趨勢。所得熱壁面絕熱翅片肋基下部數趨于0的結果與文獻[24]的研究結果一致。

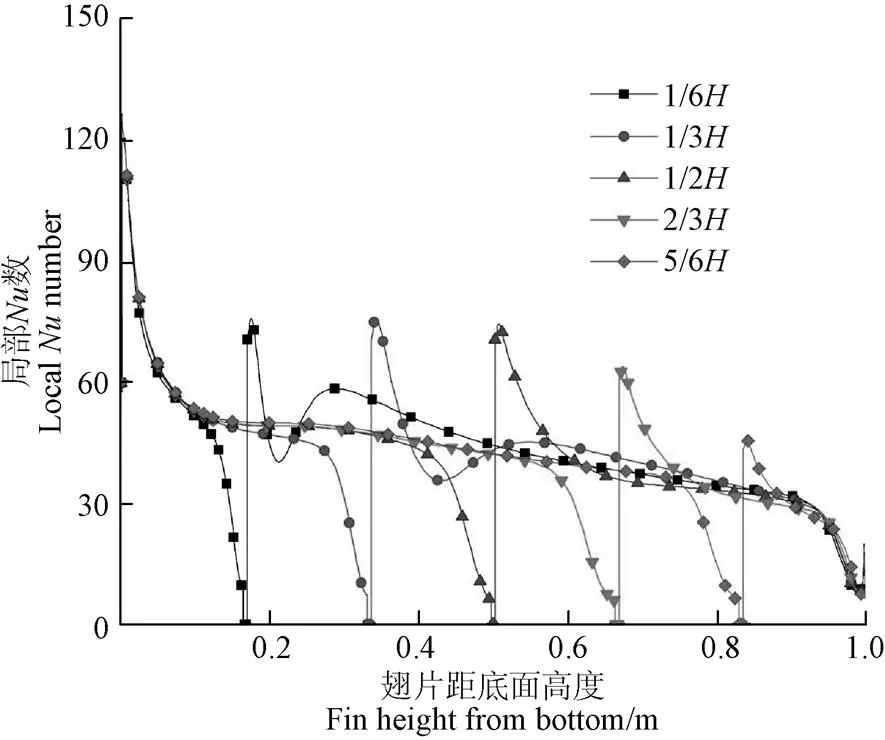
圖3 熱壁面絕熱翅片位置對熱壁面局部Nu數的影響

圖4為導熱翅片位于熱壁面不同位置時局部數沿熱壁面高度方向的變化曲線。與絕熱翅片情況類似，沿邊界層發展方向局部數呈下降趨勢，<0.1范圍內熱壁面的局部數幾乎不受翅片位置影響。這是因為熱壁面底部區域為層流狀態，具有較薄的熱層，溫度梯度大，傳熱能力就強。與絕熱翅片不同的是數只在翅片下方發生突變，翅片上方增幅較小。這是因為導熱翅片下、上表面溫差遠小于絕熱翅片的情況，上升氣流繞過翅片后形成的渦旋對翅片上部傳熱的貢獻較小。

導熱翅片對于熱壁面平均數的提高率影響見表 2。由表2可以看出，絕熱翅片位于1/6高度時熱壁面平均值最大，為31.85，導熱翅片位于1/3高度時熱壁面平均值最大，為34.93。導熱翅片的平均數較絕熱翅片提高了9.67%。所以，在封閉空間內用于固定散熱元件的基礎盡可能設計為導熱系數較高的材料，并布置在熱壁面距底部約1/3位置處更有利于散熱元件的冷卻。

圖4 熱壁面導熱翅片位置對熱壁面局部Nu數影響

表2 翅片位置對熱壁面平均Nu數提高率的影響

3.2 翅片數量對腔內對流和傳熱的影響

根據3.1節的分析結果，熱壁面布置導熱翅片在強化傳熱效果上優于絕熱翅片，因此，下文僅針對導熱翅片分析翅片位置及數量對封閉腔內自然對流傳熱的影響。

當封閉腔底面有大功率電子元器件散熱時，兩側壁電子元器件的固定位置對系統的可靠性和使用壽命有一定的影響。基于這一背景，本節在熱、冷壁面分別布置1個翅片，不同翅片位置組合工況設置如表3所示。其中熱壁面翅片保持恒溫323.15 K，冷壁面翅片保持恒溫283.15 K，熱源位于腔體底面中心，其表面溫度為353.15 K。

圖5為4種工況在準定常階段時腔體內部的等溫線圖。由圖5可知，腔內熱壁面附近流體在受到熱壁加熱和熱源輻射的共同作用下沿熱壁面向上流動，遇到翅片時原有熱邊界層和速度邊界層被破壞，隨即形成新的發展邊界層和渦旋結構并強化了熱壁面與空氣之間的換熱過程。熱氣流在浮升力作用下繼續向上爬升，沿著腔體頂部向冷壁面一側運動，在腔體頂部與冷壁面交界處開始形成沿冷壁面向下發展的邊界層，熱壁面翅片對熱壁面邊界層結構的影響與冷壁面翅片對冷壁面邊界層結構的影響產生了強烈的耦合作用。如圖 5a所示，當熱壁面翅片距離底面較近時沿熱壁面的邊界層能在下游得到充分發展，當冷壁面翅片距離底面較近時沿冷壁面的邊界層在下游的發展得到了抑制。隨著冷壁面翅片上移，腔體頂部高溫區變小，底部附近溫度梯度變小，如圖5b所示。另外，從圖5c及5d也可看出，冷壁面翅片位置對溫度場的影響要比熱壁面翅片位置的影響顯著。

表3 冷熱壁面翅片相對位置

Table 3 Relative fin position on cool and hot walls

工況Working conditionab 11/3H1/3H 21/3H2/3H 32/3H1/3H 42/3H2/3H

圖5 冷熱壁面翅片位置對溫度場的影響

Fig. 5 Influence of fins position of hot and cold walls on temperature profile

圖6為準定常階段時4種工況下的腔體內部流函數圖。由圖6可知，兩側壁翅片位置的不同組合對空腔內流動結構的影響存在較大差異。工況1和工況2中流體繞過熱壁面翅片時被加速，但工況1冷壁面邊界層起始段對流較弱，而工況2冷壁面邊界層下游段對流較強，這與文獻[32]的研究結論一致。由圖6c可知，冷壁面邊界層在下游得到了抑制，流體在熱壁面附近浮升力誘導下沿熱源頂部朝熱壁面方向運動。工況4中熱壁面邊界層上游和冷壁面邊界層下游均得到了充分發展，流體被加速，這一區段的傳熱被得到顯著強化。

a. 工況1a. Working condition 1b. 工況2b. Working condition 2c. 工況3c. Working condition 3d. 工況4d. Working condition 4

圖7為熱壁面1/3處布置翅片與熱壁面1/3、冷壁面2/3處同時布置翅片在有無內熱源情況下沿封閉腔底面中心鉛錘線上的水平速度變化曲線。由于空腔側壁上翅片的存在，腔內的對流速度分布在單翅片、雙翅片情況下表現出了較大的差異。可以看出，單翅片與雙翅片對空腔頂部附近水平速度的影響微弱，對腔體底部附近區域水平速度場結構的擾動激烈，且影響趨勢很接近，這一現象與無熱源時并不一致。翅片對腔體核心區水平速度的影響存在較大差異：單翅片對于腔體核心區較低位置的擾動較明顯，而雙翅片則對于上部區域的流場擾動更為強烈。不同數量翅片通過對流場結構的改變導致了封閉腔內溫度場的不同分布特征。

圖7 翅片數量和位置對水平速度的影響

圖8a為不同工況下局部數沿熱壁面高度方向的變化曲線。可以看出，冷熱壁面導熱翅片位置對=0.1以下區域局部傳熱能力幾乎沒有影響，熱壁面底部區域局部值最大，這是因為熱壁面速度邊界層及溫度邊界層均起始于熱壁面底部，而熱壁面底部屬于層流狀態，存在很薄的熱層，從而使得這一區域表現出了較強的傳熱能力。工況1和工況2由于其熱壁面上翅片位置相同從而表現出類似的局部傳熱特性，工況3和工況4的局部傳熱特性較一致也是源于這一因素。

圖8b為冷熱壁面導熱翅片不同位置時熱壁面平均數比較。可以看出，當熱壁面導熱翅片位于1/3高度處、冷壁面導熱翅片位于2/3高度處時，熱壁面平均數達到了39.94，壁面與腔體內部的平均傳熱效率最高，腔體內部的對流換熱最強。因此，在散熱空腔內雙側布置翅片時采取工況2的布置方式可以最大程度地對散熱元件進行自然對流冷卻降溫，以保證散熱元件的安全使用。

圖8 翅片位置對熱壁面局部Nu數及平均Nu數的影響

與表2中單翅片各工況所得熱壁面的平均數相比，圖8b所示雙翅片各工況的強化傳熱效果均有明顯改善。例如對于單導熱翅片位于1/3H的最優工況及雙導熱翅片的最優工況2，對應的熱壁面平均數分別為34.93和39.94，雙翅片較單翅片提高了14.34%。這說明在封閉腔內利用自然對流中流場與溫度場間的耦合關系，采用在熱、冷壁面上合理位置處同時布置翅片可以有效提高換熱效率，對于存在散熱元件冷卻問題的封閉腔內結構設計具有重要的理論指導意義。

4 結 論

通過在有內熱源的封閉方腔內側壁上布置導熱翅片或絕熱翅片，數值分析了不同翅片位置、數量及不同翅片材質對封閉腔內湍流自然對流傳熱特性的影響。得到了如下主要結論：

1）在封閉腔側壁布置翅片，可以通過改變速度邊界層與溫度邊界層結構來強化封閉腔內對流換熱過程。在單側壁面布置單個翅片與在兩側壁面同時布置翅片對于封閉腔側壁傳熱能力的提升幅度存在差異。

2）絕熱翅片位于熱壁面距底面以上1/6高度處時熱壁面的平均傳熱能力最強。導熱翅片位于熱壁面距底面以上1/3高度處時熱壁面的平均傳熱能力最強。熱壁面翅片位于熱壁面距底面以上1/3高度與冷壁面翅片位于冷壁面距底面以上2/3高度組合使熱壁面的平均傳熱能力最強。

3）在熱壁面距底面以上1/3高度處布置導熱翅片比在同位置布置絕熱翅片時熱壁面平均數提高了9.67%；在熱壁面距底面以上1/3高度處布置導熱翅片、冷壁面距底面以上2/3處布置導熱翅片時熱壁面平均數比只在熱壁面距底面以上1/3處布置導熱翅片的平均數提高了14.34%。

封閉腔內側壁布置翅片在強化對流傳熱的同時，翅片附近漩渦的存在會導致局部熱滯留現象，在實際應用中對應電子元器件與母材的連接處局部散熱效果下降，從而降低元器件的使用可靠性。因此，針對特定的封閉空間內各表面不同發射率時如何確定翅片結構參數、安裝方式等還需要進一步的探索。

[1] Bachelor G K. Heat transfer by free convection across a closed cavity between vertical boundaries at different temperatures[J]. Quarterly of Applied Mathematics, 1954, 12(3): 209－233.

[2] 王迪. 物理幾何條件對多熱源小空間自然對流換熱的影響[D].長春：吉林建筑大學，2016. Wang Di. Influence of Physical Geometry on Natural Convection Heat Transfer in a Small Space with Multiple Heat Sources[D]. Changchun: Jilin Jianzhu University, 2016. (in Chinese with English abstract)

[3] Cheikh N B, Beya B B, Lili T. Influence of thermal boundary conditions on natural convection in a square enclosure partially heated from below[J]. International communications in Heat and Mass Transfer, 2007, 34(3): 369－379.

[4] 李娜，過增元，李志信，方腔自然對流中力的尺度效應[J]. 清華大學學報，2002，42(11)：1508－1514. Li Na, Guo Zengyuan, Li Zhixin. Size effect of forces on natural convection in a square cavity[J]. Journal of Tsinghua University, 2002, 42(11): 1508－1514. (in Chinese with English abstract)

[5] Sharma A K, Velusamy K, Balaji C. Turbulent natural convection in an enclosure with localized heating from below[J]. International Journal of Thermal Sciences, 2007, 46(12): 1232－1241.

[6] Paroncini M, Corvaro F, Montucchiari A, et al. A numerical and experimental analysis on natural convective heat transfer in a square enclosure with partially active side walls[J]. Experimental Thermal and Fluid Science, 2012(36): 118－125.

[7] Xu Feng, Saha S C. Transition to an unsteady flow induced by a fin on the sidewall of a differentially heated air-filled square cavity and heat transfer[J]. International Journal of Heat and Mass Transfer, 2014(71): 236－244.

[8] Xia Keqing, Lam S, Zhou Shengqi. Heat-flux measurement in high-Prandtl-number turbulent Rayleigh-Bénard convection [J]. Physical Review Letters, 2002, 88(6): 1501-1504.

[9] 王燁，王良壁. 一種用于分析封閉腔內湍流自然對流換熱的新模型[J]. 應用力學學報，2014，31(5)：814－818. Wang Ye, Wang Liangbi. A new-model for the turbulent natural convection heat transfer in enclosure[J]. Chinese Journal of Applied Mechanics, 2014, 31(5): 814－818. (in Chinese with English abstract)

[10] 陽祥，陶文銓. 高瑞利數下封閉腔內自然對流的數值模擬[J].西安交通大學學報，2014，48(5)：27－31. Yang Xiang, Tao Wenquan. Numerical simulations for natural convection with high Rayleigh number in a tall rectangular cavity[J]. Journal of Xi’an Jiaotong University, 2014, 48(5): 27－31. (in Chinese with English abstract)

[11] Heiland H G, Rubes D, Wozniak G. Convection experiments in an inclined narrow cavity[J]. Heat Mass Transfer, 2012, 48(12): 2007－2012.

[12] Kwak H S, Kuwahara K, Hyun J M. Resonant enhancement of natural convection heat transfer in a square enclosure[J].International Journal of Heat and Mass Transfer, 1998, 41(18): 2837－2846.

[13] Fu Wushung, Cheng Chaosheng, Shieh W J. Enhancement of natural convection heat transfer of an enclosure by a rotating circular cylinder[J]. International Journal of Heat and Mass Transfer, 1994, 37(13): 1885－1897.

[14] Xu Feng, Patterson J C, Lei Chengwang. Temperature oscillations in a differentially heated cavity with and without a fin on the sidewall[J]. International Communications in Heat and Mass Transfer, 2010, 37(4): 350－359.

[15] Ampofo F. Turbulent natural convection of air in a non-partitionedor partitioned cavity with differentially heated verticaland conducting horizontal walls[J]. Experimental Thermal and Fluid Science, 2005, 29(2): 137－157.

[16] Liu Yang, Lei Chengwang, Patterson J C. Plume separation from an adiabatic horizontal thinfin placed at different heights on the sidewall of a differentially heated cavity[J]. International Communications in Heat and Mass Transfer, 2015, 61: 162－169

[17] Jani S,Mahmoodi M,Amini M, et al. Numerical investigation of natural convection heat transfer in a symmetrically cooled square cavity with a thin fin on its bottom wall[J]. Thermal Science, 2014, 18(4): 1119－1132.

[18] Xu Feng, Patterson J C, Lei Chengwang. Effect of the fin length on natural convection flow transition in a cavity[J]. International Journal of Thermal Sciences,2013, 70: 92－101.

[19] Khanafer K, AlAmiri A, Bull J. Laminar natural convection heat transfer in a differentially heated cavity with a thin porous fin attached to the hot wall[J]. International Journal of Heat and Mass Transfer, 2015, 87: 59－70.

[20] Lorenzini G, Machado B S, Isoldi L A, et al. Structure design of rectangular fin intruded into mixed convective lid-driven cavity flows[J]. Journal of Heat Transfer, 2016, 138(10): 2501-2512.

[21] 黃格永. 受限空間電子元件自然對流散熱特性研究[D]. 重慶：重慶大學，2016. Huang Geyong. Characteristics of Natural Convection Heat Dissipation of Electronic Components in Confined Space[D]. Chongqing: Chongqing University, 2016. (in Chinese with English abstract)

[22] Nag A, Sarkar A, Sastri V M K. Natural convection in a differentially heated square cavity with horizontal partition plate on the hot wall[J]. Computer Methods in Applied Mechanics and Engineering, 1993, 110(1-2): 143－156.

[23] Frederick R L, Valencia A. Heat transfer in a square cavity with a conducting partition on its hot wall[J]. International communications in Heat and Transfer, 1989, 16(3): 347－354.

[24] Xu Feng, Patterson J C, Lei Chengwang. Unsteady flow and heat transfer adjacent to the sidewall of a differentially heated cavity with a conducting and an adiabatic fin[J]. International Journal of Heat and Fluid Flow, 2011, 32(3): 680－687.

[25] Elatar A, Teamah M A, Hassab M A. Numerical study of laminar natural convection inside squareenclosure with single horizontal fin[J].International Journal of Thermal Sciences, 2016 (99): 41－51.

[26] Peng Hao, Ling Xiang, Li Juan. Numerical simulation and experimental verification onthermal performance of a novel fin-plate thermosyphon[J]. Applied Thermal Engineering, 2012(40): 181－188.

[27] Frederick R L.Heat transfer enhancement in cubical enclosures with verticalfins[J]. Applied Thermal Engineering,2007, 27(8-9): 1585－1592.

[28] Varol Y, Oztop H F.Control of buoyancy-induced temperature and flow fieldswith an embedded adiabatic thin plate in porous triangular cavities[J]. Applied Thermal Engineering,2009, 29(2-3): 558－566.

[29] Tian Y S, Karayiannis T G. Low turbulence natural convection in an air filled square cavity-Part I: the thermal and fluid flow fields[J]. International Journal of Heat and Mass Transfer, 2000, 43 (6): 849－866.

[30] Omri M, Galanis N. Numerical analysis of turbulent buoyant flows in enclosures[J]. Influence of grid and boundary conditions, 2007(46): 727－738.

[31] 王燁，徐燃. 青藏線空調列車室內氣流組織的沿線變化數值分析[J]. 重慶大學學報，2014，37(9)：59－67. Wang Ye, Xu Ran. Numerical study of airflow distribution in air-conditioned train in Qinghai-Tibet Railway[J]. Journal of Chongqing University, 2014, 37(9): 59－67. (in Chinese with English abstract)

[32] Xu Feng, Patterson J C, Lei Chengwang. An experimental study of the unsteady thermal flow around a thin fin on a sidewall of a differentially heated cavity[J]. International Journal of Heat and Fluid Flow, 2008, 29(4): 1139－1153.

Numerical analysis of natural convection cooling effect in closed cavity of electronic equipment

Wang Ye1,2, Zhao Xingjie1, Lin Huxiang1, Song Rongfei1, Guan Guoxiang1

(1.,,, 730070,; 2.,,,, 730070,)

Natural convection in closed cavity has been received considerable attention due to its widely applications in industry, such as in solar energy collectors design, cooling of electronic instruments, energy saving of building and nuclear reactor design, the study of natural convection mechanism in enclosed cavity is of great practical significance for improving the comprehensive performance of these systems. With the rapid development of science and technology, more and more heat sources and components are located in the same enclosed cavity, which will lead to large number of heat generation. How to arrange the heat source elements is very important to the cooling and reliability of the system by the natural convection heat transfer. Lots of studies have shown that the fins attached to the vertical walls inside the cavity can enhance the heat transfer rate in the cavity. In order to study the effect of the material and space position of heat radiation in enclosed space on the heat transfer characteristics of natural convection, the RNG-model of FLUENT14.5 was adopted to analyze the temperature field, flow field, local Nusselt numbers and the average Nusselt numbers of the vertical wall of the air-filled cavity (left side was hot wall, right side was cold wall and the top side was the heat source) with aspect ratio of 1. The results showed that the heat transfer enhancement of the cavity was strongly dependent on the position and material of the fins attached to the vertical walls. The influence of single fin and double fin on the horizontal velocity near the top of the cavity was weak, and the disturbance to the horizontal velocity field near the bottom of the cavity was intense, and the influence trend was very close. This phenomenon was not consistent with that of without heat source. The effect of fins on the horizontal velocity in the core region of the cavity was quite different: the disturbance of single fin on the lower position of the core region of the cavity was more obvious, while the disturbance of double fins on the upper region was more intense. Different number of fins lead to different distribution characteristics of temperature field in the enclosed cavity by changing the flow field structure. When the adiabatic fin was located at 1/6 height above the bottom of the hot wall, the average heat transfer capacity of the hot wall was the strongest. When the heat conducting fin was located at 1/3 height above the bottom of the hot wall, the average heat transfer capacity of the hot wall was the strongest. The combination of 1/3 height above the bottom of the hot wall and 2/3 height above the bottom of the cold wall made the average heat transfer capacity of the hot wall the strongest. The averagenumber of thermal conductive fins arranged at 1/3 height above the bottom of the hot wall was maximum, which was 34.93 and 9.67% higher than that of adiabatic fin arranged at the same location. The averagenumber of thermal conductive fins arranged at 1/3 height above the bottom of the hot wall and 2/3 above the bottom of the cold wall was maximum, which was 14.3% and higher than that of thermal conductive fins arranged only at 1/3 above the bottom of the hot wall. The study has a certain theoretical significance for improving the natural convection cooling effect of electronic components in industrial and agricultural engineering and optimizing the spatial location of heat dissipation components.

numerical simulation; temperature; heat convection; enclosed cavity; fin

2018-10-18

2018-11-28

國家自然科學基金（51476073，51266004）；甘肅省建設科技攻關項目（KJ2016-2）

王燁，教授，博士，博士生導師，主要從事自然對流及暖通空調研究。Email：wangye@mail.lzjtu.cn

10.11975/j.issn.1002-6819.2019.06.026

TK124

A

1002-6819(2019)-06-0214-08

王 燁，趙興杰，藺虎相，宋榮飛，管國祥. 電子設備封閉腔內自然對流冷卻效果數值分析[J]. 農業工程學報，2019，35(6)：214－221. doi：10.11975/j.issn.1002-6819.2019.06.026 http://www.tcsae.org

Wang Ye, Zhao Xingjie, Lin Huxiang, Song Rongfei, Guan Guoxiang. Numerical analysis of natural convection cooling effect in closed cavity of electronic equipment[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(6): 214－221. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.06.026 http://www.tcsae.org