地月系平動點軌道動力學建模與控制策略研究

于登云 周文艷 高珊

(1中國航天科技集團有限公司,北京 100048)(2北京空間飛行器總體設計部,北京 100094)

平動點是第三體在受2個大天體的萬有引力作用時在空間中的引力平衡點。1765年,歐拉發現在一個旋轉二體重力場中存在3個共線的天平動點;1772年,拉格朗日指出在一個旋轉二體重力場中存在另外2個天平動點。這5個點統稱為拉格朗日點(L1～L5),也稱平動點。其中,L1、L2和L3是共線平動點,L4和L5為三角平動點。平動點特殊的動力學特性和在三體問題中相對固定的幾何位置,使其在中繼通信、在軌服務、天文觀測、星際導航、星際轉移等深空探測任務中具備良好的工程應用價值。雖然此前開展了一些研究探索[1-5],但鑒于技術復雜性等因素,未有利用地月系平動點開展地月中繼服務的先例。

嫦娥四號是世界首次著陸月球背面進行月球探測的任務,由于月球背面始終背向地球,探測器無法直接與地面通信,需要中繼衛星作為地面站與月球背面探測器之間通信的橋梁。為保障中繼任務順利開展,其軌道設計不僅要考慮日-地-月-星相對幾何關系,還要考慮各種工程約束條件,如測控要求、運載火箭發射要求、推進劑約束、光照條件等;同時,軌道振幅參數、相位等設計變量與速度增量、軌道光照等約束條件具有極為復雜的耦合關系,在工程設計中要對軌道特性進行分析來解耦這些約束。因此,必須要建立考慮三體引力的高精度動力學模型進行軌道計算、分析,尋找其中的規律和軌道特性,確定滿足任務需求的中繼衛星最佳軌道方案和最省推進劑的軌道控制策略。

1 軌道動力學建模與求解

1.1 非線性動力學通用模型

在慣性空間中,n個物體在無其他外力的作用下,公共質心的加速度為零,各質量體在相互作用下繞質心作圓周運動,示意見圖1。設n個物體的質量分別為m i(i＝1,…,n),它們相對于慣性坐標系OXYZ的矢徑分別為r i(i＝1,…,n),慣性坐標系的原點為它們的公共質心O。

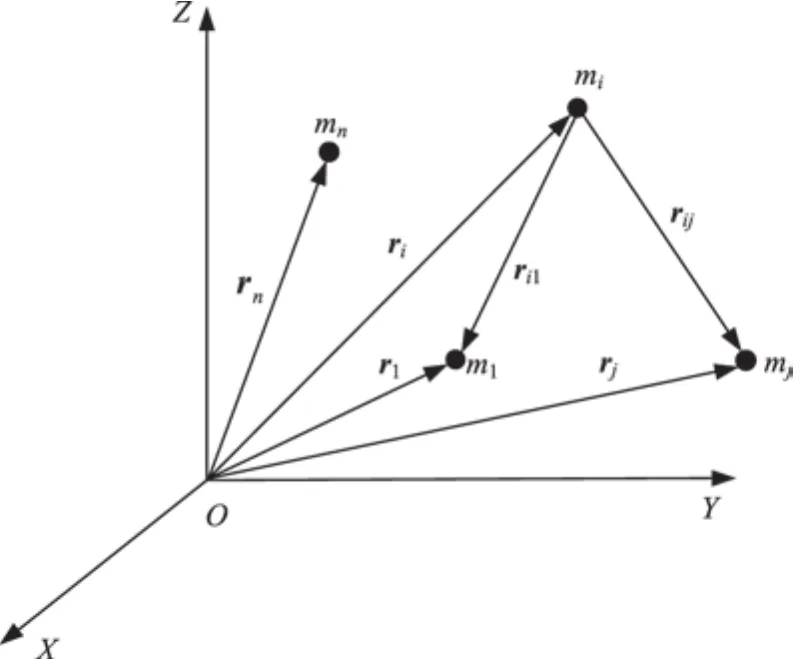
圖1 n體問題示意Fig.1 Illustration of multi-body problem

第i個物體的單位質量加速度為

式中:G為引力常數;第i個物體到第j個物體的矢徑r ij＝r j－r i。

一般情況下,要研究衛星相對于某個主物體的運動,坐標系原點在主物體質心。把第n個物體當作衛星,第1個物體當作主物體,則衛星相對于主物體慣性坐標系中的加速度為

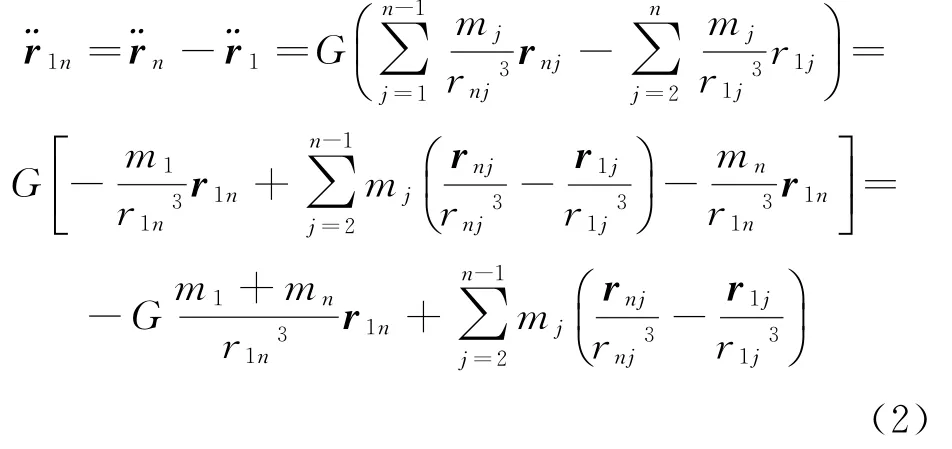
這就是n體運動方程。研究衛星在平動點的運動是一個四體問題,要包括日、地、月的中心引力,衛星在地心慣性坐標系下的運動方程如下。

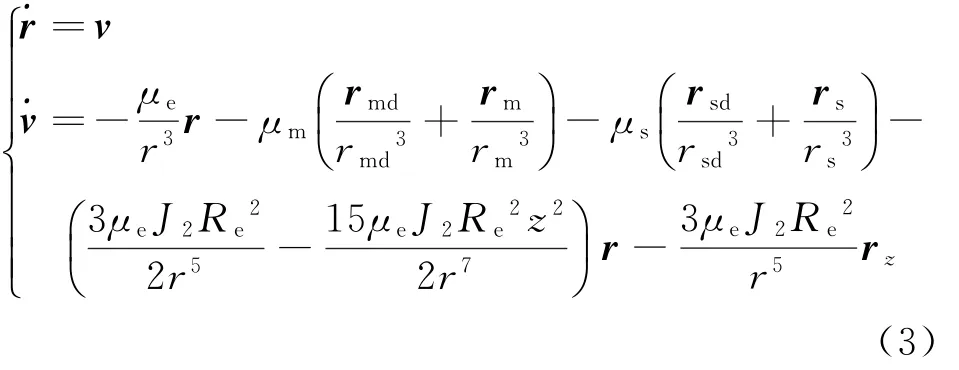
式中:r和v為衛星的位置矢量和速度矢量;rm和rs為地心指向月球和太陽的矢量;rmd和rsd為月心和日心指向衛星的矢量;μe,μm,μs為地球、月球和太陽的引力常數;J2為地球帶諧系數;矢量r z可表示為[0 0z]T;地球平均赤道半徑Re＝6378.140 km。

1.2 微分修正方法

衛星在不同運行階段的計算是選取不同的初始和末端狀態,利用狀態轉移矩陣進行迭代求解,從而找到精確的結果[6-7]。初始狀態參數矩陣p和末端狀態參數矩陣q之間的關系可以表示為q＝f(p),兩狀態之間的誤差關系可線性化表示為Δq＝利用這個關系,在合適的初值基礎上,通過若干次迭代就可以求出十分精確的數值解。Δq就是誤差傳遞矩陣,它的數值解可以通過數值積分得到,見式(4)。

式中:r0和v0為衛星在初始時刻的位置和速度;3個矩陣S,R,T的乘積結果為誤差傳遞矩陣Ts,其中S和T分別為末端和初始狀態轉移矩陣,R為狀態轉移矩陣,見式(5),其微分形式見式(6)。

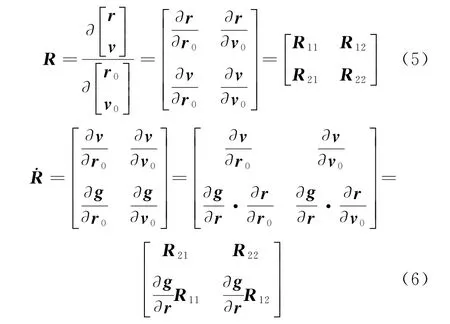
式中:g為。

首先,給出軌道積分的初值,將式(3)和式(6)一起積分,得到任意時刻衛星的位置、速度和狀態轉移矩陣R,再利用軌道積分的初值求出矩陣T,軌道積分到末端狀態求出矩陣S,這3個矩陣相乘就得到了誤差傳遞矩陣Ts;然后,把積分得到的末端狀態減去要求達到的值,差值就是誤差傳遞矩陣Δq,則初始狀態的修正量Δp＝Ts－1Δq。用這個修正量來修正初始狀態,然后再重復上述積分,這樣反復迭代到末端狀態達到一定的精度,最終求解出滿足末端狀態的軌道。

1.3 解析計算模型

考慮3個物體的動力學系統(即三體系統),其中2個為主引力天體,第3個為衛星,其質量遠小于前2個天體,可認為前2個天體的運行不受衛星影響。進一步假定2個天體圍繞該系統的公共質心作勻速圓周運動,則稱為圓型限制性三體問題。以地月系為例描述這一問題,建立地月質心會合坐標系OBXBYBZB,其坐標原點位于三體系統的公共質心,XB軸為大天體指向小天體方向,ZB軸沿2個天體運行的角動量方向,YB軸滿足右手坐標系定義。在此基礎上定義平動點坐標系OLXLYLZL,將質心會合坐標系平移至相應的平動點,其余指向不變。

圖2以地月系L2為例給出地月質心會合坐標系

OBXBYBZB、平動點坐標系OLXLYLZL和地心慣性坐標系OXYZ的關系。平動點坐標系(地月L2會合坐標系)的原點在L2,L2與地月系公共質心的距離為1.155682 110 911D(D為地月距離,由星歷表DE405得到),L2與月心的距離為0.167 832 682 341D;地月L2會合坐標系的XL軸為瞬時地月矢量方向,ZL軸為白道面法向。

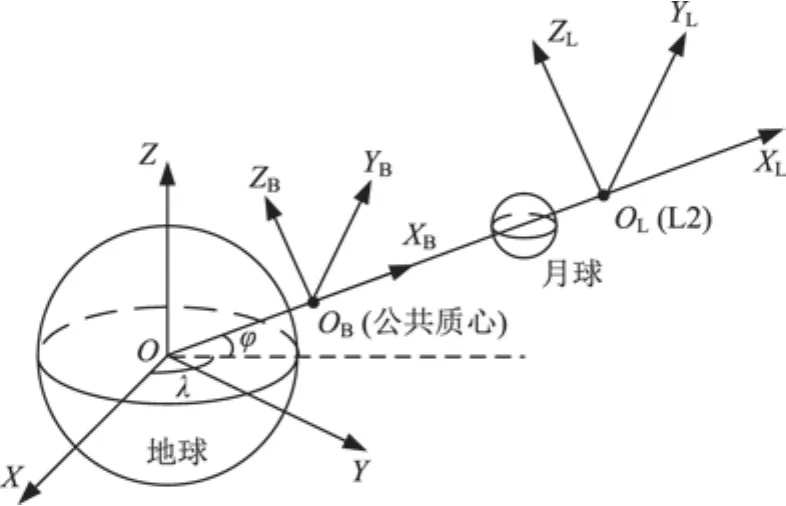
圖2 3個坐標系的關系Fig.2 Relationship among three coordinate systems

圓型限制性三體問題動力學模型普遍表達為

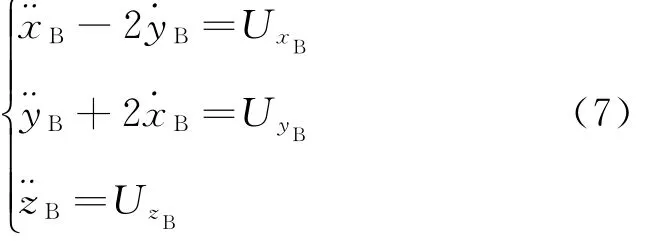
式中:xB,yB,zB為衛星在地月質心會合坐標系中的位置分量;擬勢函數U＝(1－μ)/r1B＋μ/r2B＋(xB2＋yB2)/2,其中μ為三體系統的2個天體中較小天體的質量占比,r1B和r2B分別為地月質心會合坐標系中2個天體的矢徑大小;U xB,U yB,U zB表示擬勢函數U對xB,yB,zB求偏導。

平動點軌道類型有很多,最常見和工程上已經實現的是Halo軌道和Lissajous軌道。Halo軌道分為南向軌道和北向軌道,以地月系為例,判斷Halo軌道的最簡單準則是,當衛星經過地月視線時,其速度近似平行于白道面并垂直于地月視線。Lissajous軌道的通常定義是,平面內振動頻率和垂直平面的振動頻率不同。平動點軌道還有Lyapunov軌道、垂直軌道、軸向軌道、蝶形軌道等類型,關于各種類型平動點軌道的定義,目前沒有統一[8]。本文結合“鵲橋”衛星的任務特點,主要圍繞Halo軌道開展研究,對于Lissajous軌道模型不再贅述,具體可參見文獻[9]。下面主要針對Halo軌道的解析解進行介紹。

三體動力學方程無法直接得到解析解,但可以利用勒讓德(Legendre)多項式將平動點附近的運動方程線性化近似,再通過求解線性化方程組給出周期軌道的近似解析解。將式(7)所采用的地月質心會合坐標系平移至相應的平動點(如L2),指向保持不變,并且進行無量綱化和歸一化處理,可以得到第三體在共線平動點坐標系下的運動方程形式為

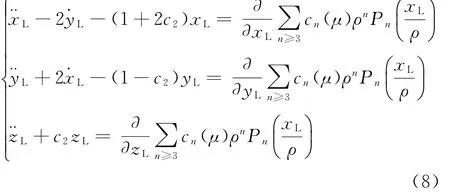
考慮運動方程中的三階項影響,利用Legendre級數得到保留三階小量的方程,見式(9)。采用Lindestedt-Poincaré方法,可進一步推導出Halo軌道的三階近似解析解,見式(10)。

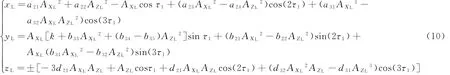
式中:A XL和A ZL分別為XL軸和ZL軸方向的振幅;τ1為相位角;a,b,k,d均為推導因子;zL取“＋”時為南向Halo軌道,取“－”時為北向Halo軌道。

需要說明的是,式(10)中利用Legendre級數對三體動力學方程進行展開,在平動點附近時,因高階項均為小量o(x n),可以在近似計算中舍去。然而,當第三體位置與平動點的距離較大時,高階項中因包含該距離及各方向分量的高次項,不再是小量,若采用舍去高階項的近似處理,則由高次項后產生的差異會使解析近似計算結果與實際情況偏差較大。

2 中繼衛星運行軌道的確定

2.1 飛行方案簡介

“鵲橋”衛星飛行階段分為發射段、地月轉移段、月球到L2轉移段、捕獲段和使命段。

(1)發射段:從運載火箭發射到星箭分離的飛行階段。

(2)地月轉移段:從星箭分離到近月點的飛行階段,1天2個發射窗口的轉移軌道飛行時間分別按照112 h和136 h設計。

(3)月球到L2轉移段:衛星到達近月點時進行近月制動,制動的速度增量不足以使衛星捕獲進入月球軌道,而是進入穩定流形,飛行3～4天到達L2附近,即到達經過地月連線并垂直于白道面的平面。

(4)捕獲段:衛星到達L2后的第1圈軌道。捕獲段通過軌道捕獲控制形成滿足任務要求的使命軌道。

(5)使命軌道段:捕獲段結束后,衛星進入使命軌道并開展中繼工作,預期工作壽命為3年。

在軌道設計過程中,需要首先根據任務需求和約束確定使命軌道,然后以使命軌道為目標,針對從地球出發的轉移軌道的任務參數和軌道控制策略進行設計。下文給出具體設計過程和結果。

2.2 使命軌道的確定

中繼軌道可選擇方案有月球凍結軌道(環月軌道)、地月L2軌道,以及介于兩者之間的近直線暈軌道(NRHO),見圖3。環月中繼軌道可采用大橢圓凍結軌道,這樣幾乎不需要進行軌道維持,但是無法保證月球背面著陸點的全時段覆蓋,存在通信盲區。地月L2中繼軌道通過合理選擇著陸區及軌道構型,可實現月球背面著陸點的全時段通信覆蓋。NRHO也是近年來備受關注的一種軌道類型,其主要優點是通過設置軌道的共振周期避免月影,但也無法實現月球背面著陸點的全時段通信覆蓋。3種中繼軌道通信覆蓋對比如表1所示。可以看出:以NRHO共振周期與月球會合周期比例9∶2為例,NRHO對嫦娥四號著陸區也有較好的覆蓋性,但對近月點幅角要求約90°,直接地月轉移軌道無法滿足幅角要求,需要采用低能轉移(弱穩定邊界轉移)的方式,轉移時間3～4個月;另外,該類型軌道對運載火箭出發能量要求較高。通過對比,中繼軌道選擇地月L2軌道。

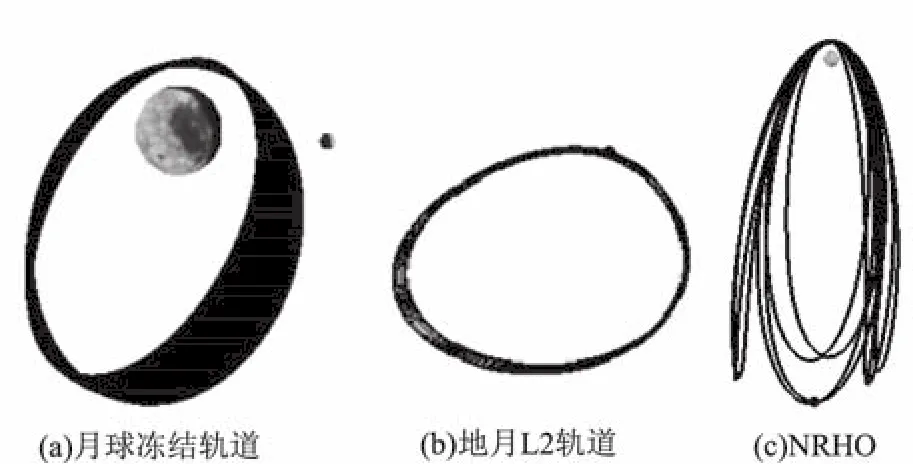
圖3 中繼軌道類型Fig.3 Types of relay orbit

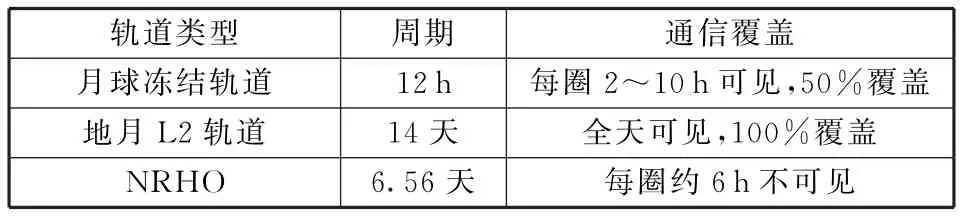
表1 中繼軌道通信覆蓋對比Table 1 Comparison of communicationscoverage of relay orbits

對于平動點軌道類型的選擇,Lissajous軌道在會合坐標系下呈Lissajous曲線的形式,在長時間飛行的情況下難以避免月掩的出現,對關鍵事件測控弧段的安排帶來不利。因此,為保障長期運行對地通信的需求,使命軌道類型選擇Halo軌道。由于嫦娥四號任務著陸區域位于南半球,為了使中繼衛星能夠有更多時間處于南半球上空,以利于中繼任務的空間幾何關系,因此使命軌道選擇南向Halo軌道。

利用解析方法,可以計算出不同形狀Halo軌道的位置和速度,見圖4。一些典型的振幅對應的遠月端和近月端的位置和速度見表2[10]。

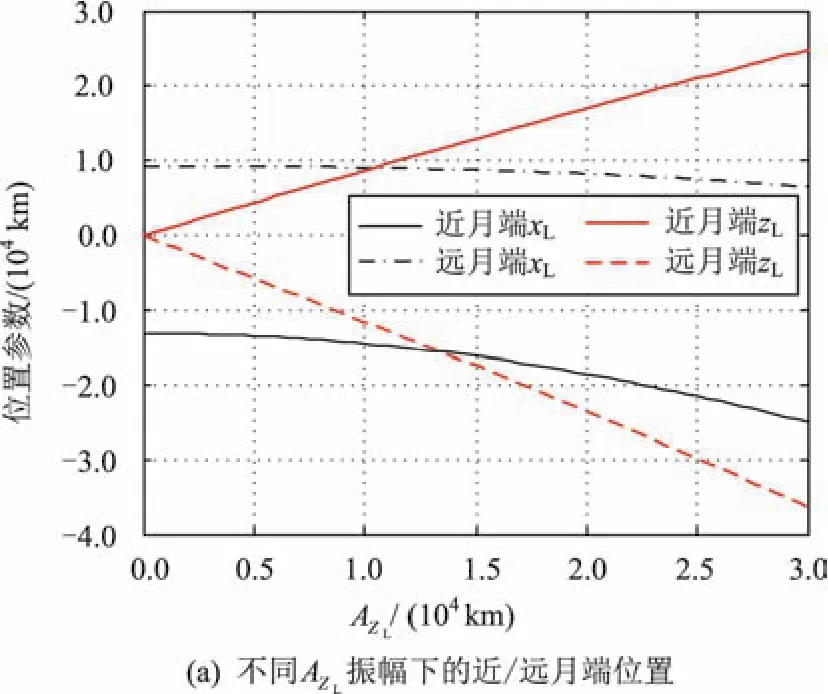
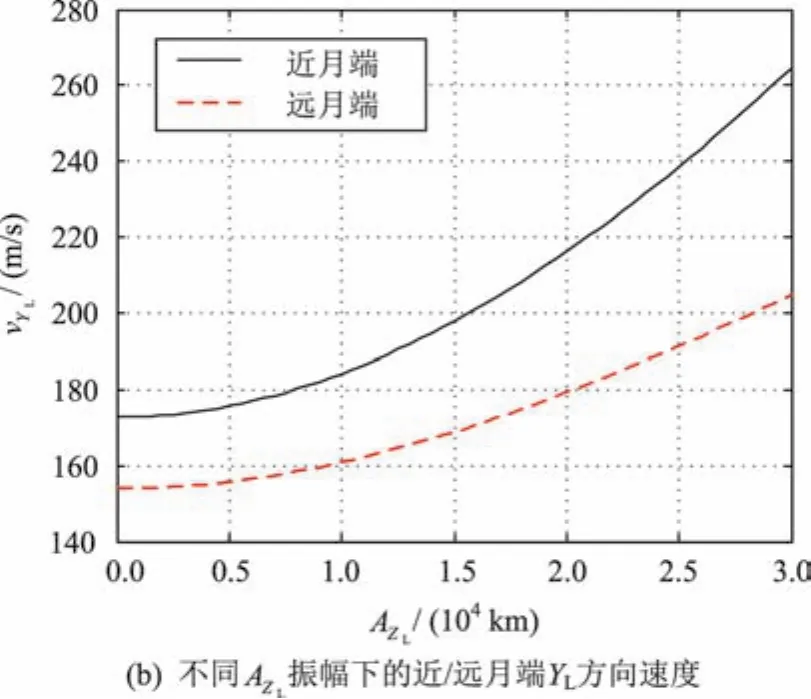
圖4 Halo軌道的位置和速度Fig.4 Halo orbit position and velocity

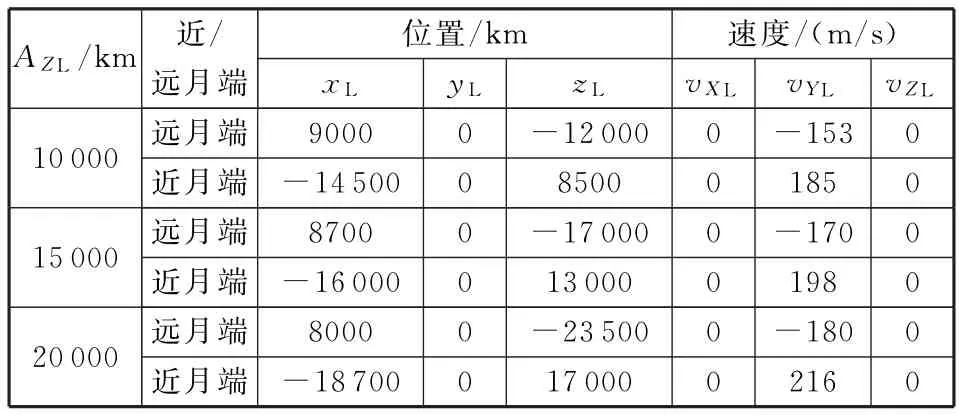
表2 不同振幅下的Halo軌道的位置和速度Table 2 Halo orbit position and velocity of different amplitudes

對2018年5－6月各窗口使命軌道本影時長進行統計,使命軌道的運行時長為3年,結果見表3。由表3可知:對于2018年5－6月的發射窗口,A ZL為13 000 km的軌道最長本影時長為4.7 h。

“鵲橋”衛星相對于嫦娥四號著陸器的距離和方位角的極坐標及仰角變化見圖5。可以看出:對于主選著陸區中心點,使命軌道段運行3年內,“鵲橋”衛星相對著陸器的仰角均大于20°。

綜合考慮光照、測控、速度增量等約束,L2環繞軌道選擇A ZL為13 000 km的南向軌道。Halo軌道的基本參數為:A XL約為12 500 km,A YL約為37 000 km,A ZL約為13 000 km,軌道的平均周期約為14天。其軌道形狀如圖6所示。考慮軌道演化和誤差的影響,使命軌道運行3年的振幅變化范圍為:A XL不超過14 000 km,A YL不超過38 000 km,A ZL不超過17 000 km。該使命軌道與著陸器通信覆蓋率達100%,且對于首發窗口在3年飛行過程中只有2次經歷地球的本影。

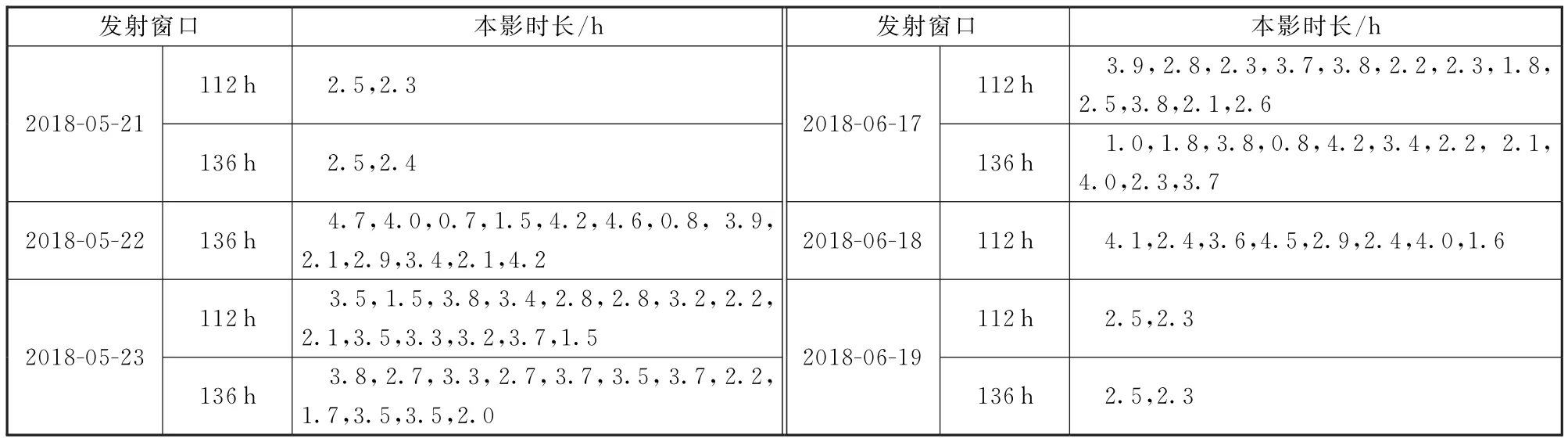
表3 Halo軌道本影時長Table 3 Eclipse time of Halo orbit

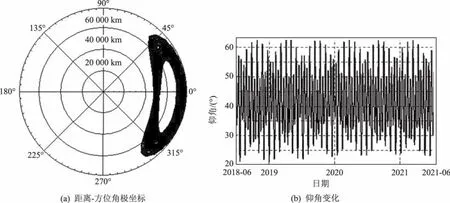
圖5 “鵲橋”衛星方位角和仰角Fig.5 Azimuth and elevation angle of Queqiao satellite

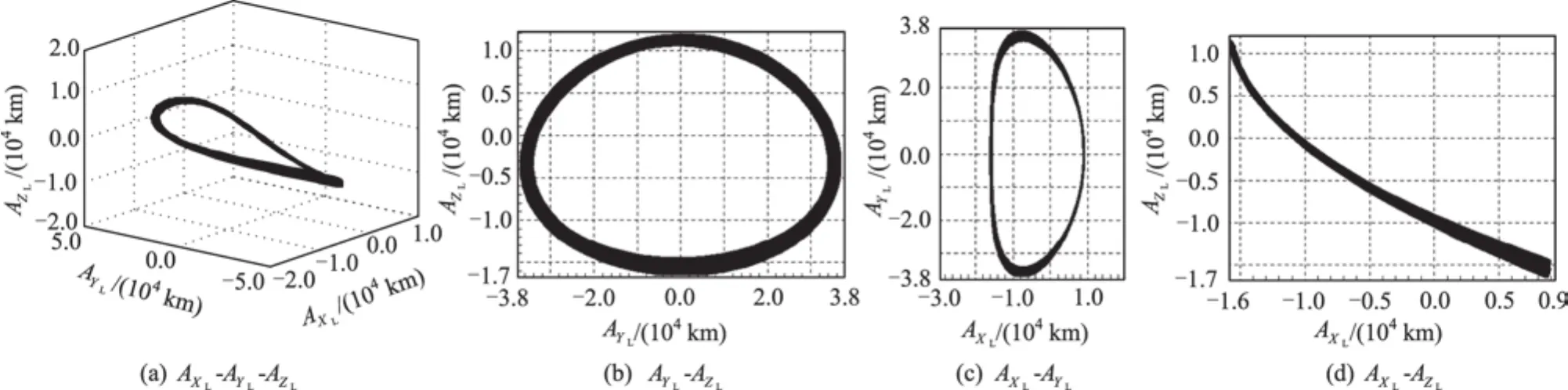
圖6 Halo軌道形狀Fig.6 Illustration of Halo orbit

2.3 轉移軌道的確定

實現地月L2軌道飛行的轉移軌道,有直接轉移、低能轉移和月球引力輔助轉移3種方案可選,見圖7。

直接轉移軌道與地月轉移軌道類似,只是其遠地點更高,因此出發能量比地月轉移軌道稍大。直接轉移軌道在到達L2時要進行捕獲控制,所需速度增量約1.0 km/s。低能轉移軌道即行星際高速公路,通過從地球發射進入拋物線軌道,使衛星運行到距離地球1.5×106km左右后再返回地月系,進入地月L2軌道,其所需速度增量小,但是近地點出發速度較大,且轉移時間一般為3～4個月。月球引力輔助轉移軌道是將衛星從地球發射進入地月轉移軌道,衛星飛行至近月點時通過近月制動完成減速變軌,所需速度增量約為0.2 km/s。衛星并不進入環月軌道,而是在飛越月球后進入地月L2附近的穩定流形,在到達L2附近時可不經變軌或只需很小的速度增量就進入環繞L2的軌道。3種轉移軌道參數比較見表4。

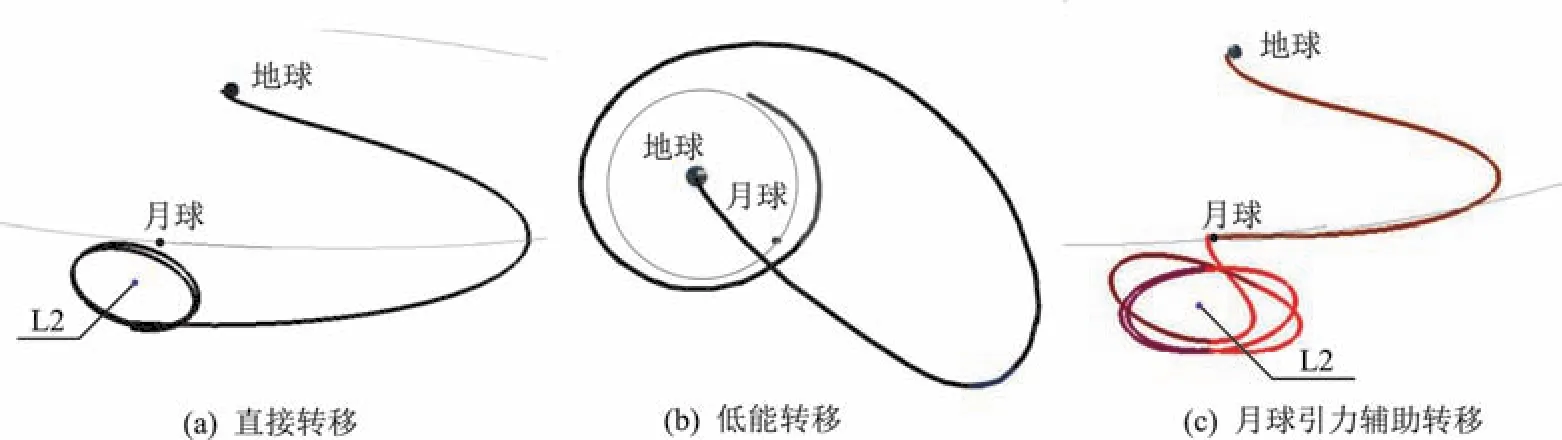
圖7 3種轉移軌道Fig.7 Three transfer trajectories

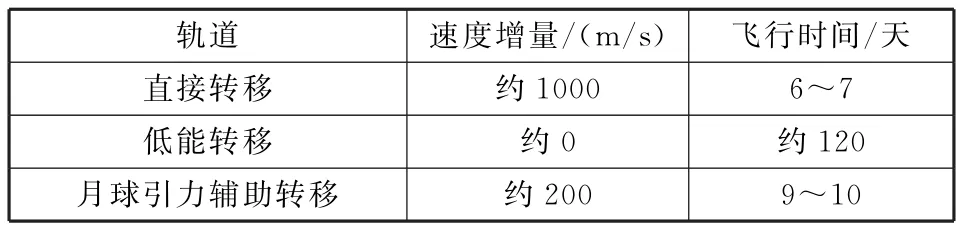
表4 轉移軌道對比Table 4 Comparison of transfer trajectories

月球引力輔助轉移軌道繼承性好,轉移時間短,速度增量需求遠小于直接轉移軌道,而且考慮到發射能量對發射質量的影響,“鵲橋”衛星的剩余質量大。

2.3.1 地月轉移段

“鵲橋”衛星的地月轉移段設計充分繼承嫦娥三號探測器的設計方法和特點,由長征-4C運載火箭送入近地點高度200 km、遠地點高度380000 km、傾角28.5°降軌發射的地月轉移軌道,經過5～6天的飛行,降軌到近月點高度100 km、軌道傾角15°。在設計過程中,根據任務需求對到達傾角進行優化,飛行時間根據近月制動時的測控條件在112 h和136 h附近進行調整。

2.3.2 月球到L2轉移段

初始狀態參數矩陣p和末端狀態參數矩陣q在月球到L2轉移段可表示為[6]

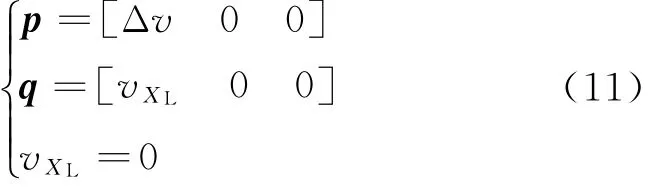
式中:Δv為近月點制動速度增量,衛星在地月轉移段運行到近月點時,位置和速度是確定的,此時在近月點沿衛星相對于月球的速度反方向進行減速制動,使衛星進入地月L2穩定流形;v XL為衛星運行到地月L2會合坐標系OLXLYLZL的XLOLZL平面時XL軸方向速度。

Δv的初值為,其中,μm為月球引力常數,rp為衛星從月球出發時的月心距,月球到L2轉移段的剩余速度平方C3取－0.175 km2/s2。

迭代計算時采用逐次迭代收斂的方法,具體過程如下。

(1)以近月制動速度增量為控制變量,目標為第1次經過地月L2會合坐標系XLOLZL平面時,相對于會合坐標系的速度v XL＝0,迭代收斂;

(2)繼續以近月制動速度增量為控制變量,目標為第2次經過地月L2會合坐標系XLOLZL平面時,相對于會合坐標系的速度v XL＝0,迭代收斂;

(3)繼續對軌道進行積分,目標為第3次經過地月L2會合坐標系XLOLZL平面時,相對于會合坐標系的速度v XL＝0,迭代收斂。

經過3次迭代收斂,求出近月制動速度增量。衛星按該增量減速制動后,從月球飛至地月L2,進入L2的穩定流形,近月點高度100 km,軌道傾角15°,地月轉移時間112 h。不同發射窗口下近月制動速度增量見圖8。可以看出,近月制動速度增量1個月變化1個周期,與月球公轉周期相同。

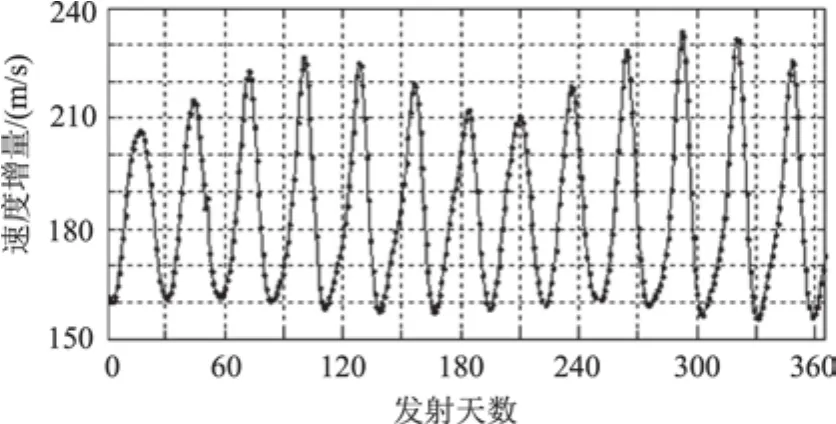
圖8 不同發射窗口的近月制動速度增量ΔvFig.8 Perilune decelerationΔv of different launch windows

3 中繼衛星軌道控制策略

“鵲橋”衛星整個飛行過程需要進行的軌道控制可分為捕獲控制、軌道修正和軌道維持3類。捕獲控制的目的是使衛星捕獲進入預定的使命軌道;軌道修正的目的是對飛行過程中的各類誤差(包括運載火箭入軌誤差、測控誤差、軌道控制誤差等)進行修正,使在誤差情況下飛行軌道仍能滿足任務要求;軌道維持則是由于地月系L2是不穩定點,在使命軌道飛行階段需要定期進行軌道維持以保證衛星在Halo軌道上的長期穩定運行。

3.1 捕獲控制

根據軌道特性和地月L2的Halo軌道構型需要,“鵲橋”衛星通過1次近月制動和2次Halo軌道捕獲控制,變軌進入特定構型的Halo軌道(南向、A XL為12500 km、A YL為38 000 km、A ZL為13 000 km),并通過合理安排2次捕獲脈沖的位置及Halo軌道進入點的相位,使3次脈沖的速度增量之和最小。

“鵲橋”衛星近月制動后進入月球到L2轉移段,為確保在到達L2附近后能夠順利進入環繞L2的軌道并開展捕獲控制,近月制動及后續轉移段的控制機動均應以保障到達L2附近后第1圈軌道的穩定為目標。近月制動采用4個20 N推力器加8個5 N推力器組合執行,推力方向沿近月點速度反方向,采用慣性定向,1次完成,通過控制推力作用時間實現預定軌道控制目標。

“鵲橋”衛星到達地月L2附近后的第1圈為捕獲段,進行2次捕獲控制,用于調整軌道位置和速度,形成滿足中繼任務的使命軌道;同時,由于捕獲控制速度增量較大,為保證軌道穩定性,在各次捕獲控制后分別安排1次軌道修正,用于修正捕獲控制殘差。

第1次捕獲控制為“3對2”的控制策略,即通過調整變軌點3個方向的速度分量瞄準第3次穿過地月L2會合坐標系XLOLZL平面時XL軸方向和ZL軸方向位置。該策略解不唯一,通過對控制變量進行優化獲得推進劑最優解。

第2次捕獲控制為“3對1”控制策略,需要首先以Halo軌道過XLOLZL平面時地月L2會合坐標系下各方向速度分量要求(對于A ZL為13000 km的南向Halo軌道,過遠月端XLOLZL平面時v XL為0 m/s,v ZL為0 m/s,v YL為－165.40 m/s)為初始目標,計算滿足各方向速度所需要的變軌速度增量,并將計算結果作為初值,通過迭代調整變軌點各方向速度,使控制后第3次穿過地月L2會合坐標系XLOLZL平面時沿XL軸方向的速度為零。

3.2 軌道修正

地月轉移段中途修正安排3次,綜合考慮各發射窗口測控弧段差異和后續可能的微調,第1次安排在星箭分離后的14 h±1 h,第2次安排在星箭分離后的38 h±1 h,第3次安排在到達近月點前24 h±1 h實施。地月轉移中途修正為“3對3”的微分修正策略,由變軌速度增量3個方向分量瞄準近月點高度100 km、軌道傾角15°和真近點角0°的軌道控制目標。

在月球到L2轉移段,根據定軌結果和測控弧段安排2次中途修正,分別在近月制動后24 h和48 h,用于修正近月制動殘差。中途修正沿速度方向施加速度增量,軌道控制目標為第3次穿過地月L2會合坐標系XLOLZL平面時沿XL軸方向的速度為零。

“鵲橋”衛星在每次捕獲后約2天進行1次軌道修正,具體修正時刻根據實際測控條件決定,并可根據每次捕獲后的誤差情況決定是否取消。軌道修正的目標與前一次捕獲控制的目標一致。

3.3 軌道維持

“鵲橋”衛星在L2工作期間,計劃每周進行1次軌道維持,3年共150次。軌道維持安排在“鵲橋”衛星過地月L2會合坐標系XLOLZL平面前后,具體時刻可根據國內地面站測控條件確定。軌道維持策略是通過調整控制時刻各方向速度增量,實現第3次穿過地月L2會合坐標系XLOLZL平面時沿XL軸方向速度為零的目標。

4 應用效果

“鵲橋”衛星于2018年5月21日由長征-4C運載火箭直接送入地月轉移軌道,經過1次地月轉移中途修正、1次近月制動、1次月球到L2轉移中途修正、2次Halo軌道捕獲控制,于6月14日進入距離月球約65 000 km的地月L2的Halo使命軌道,成為世界上首顆運行在地月L2的Halo軌道衛星,飛控實施的飛行軌跡見圖9[11],與設計結果一致。

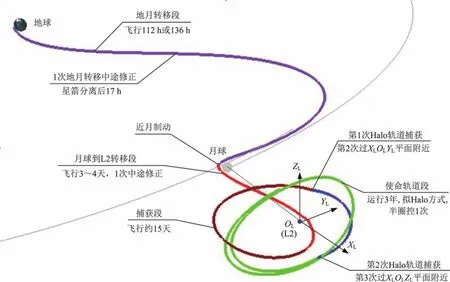
圖9 “鵲橋”衛星飛行軌跡Fig.9 Trajectory of Queqiao satellite

進入使命軌道后至2019年4月初,“鵲橋”衛星圍繞L2飛行20圈,共實施32次軌道維持。軌道維持情況見表5。針對已有的維持實施情況分析維持頻率和速度增量消耗,“鵲橋”衛星軌道維持頻率平均約9天1次,1年對應的速度增量約為18 m/s,滿足前期的速度增量預算。衛星整個飛行過程中的參數和軌道控制效果符合預期,速度增量滿足前期預算設計結果,充分驗證了衛星軌道設計和軌道控制策略設計的正確性和合理性。

“鵲橋”衛星軌道設計開創了地月平動點Halo軌道設計的先河,也是國際上首次工程實現。與其他月球探測軌道設計不同,它涉及到發射軌道和地月轉移軌道的拼接、地月轉移軌道和月球到L2轉移軌道的拼接、月球到L2轉移軌道和L2使命軌道的拼接,設計過程復雜。另外,L2軌道的不穩定,在軌道計算時,初值、計算精度都會影響計算的收斂性,僅使用狀態轉移矩陣計算很難收斂。“鵲橋”衛星的軌道設計結果滿足工程任務需求,為中繼任務的成功實施提供了保證,并經過了飛行試驗的驗證,設計模型和設計方法在后續平動點相關任務中具有良好的應用前景。

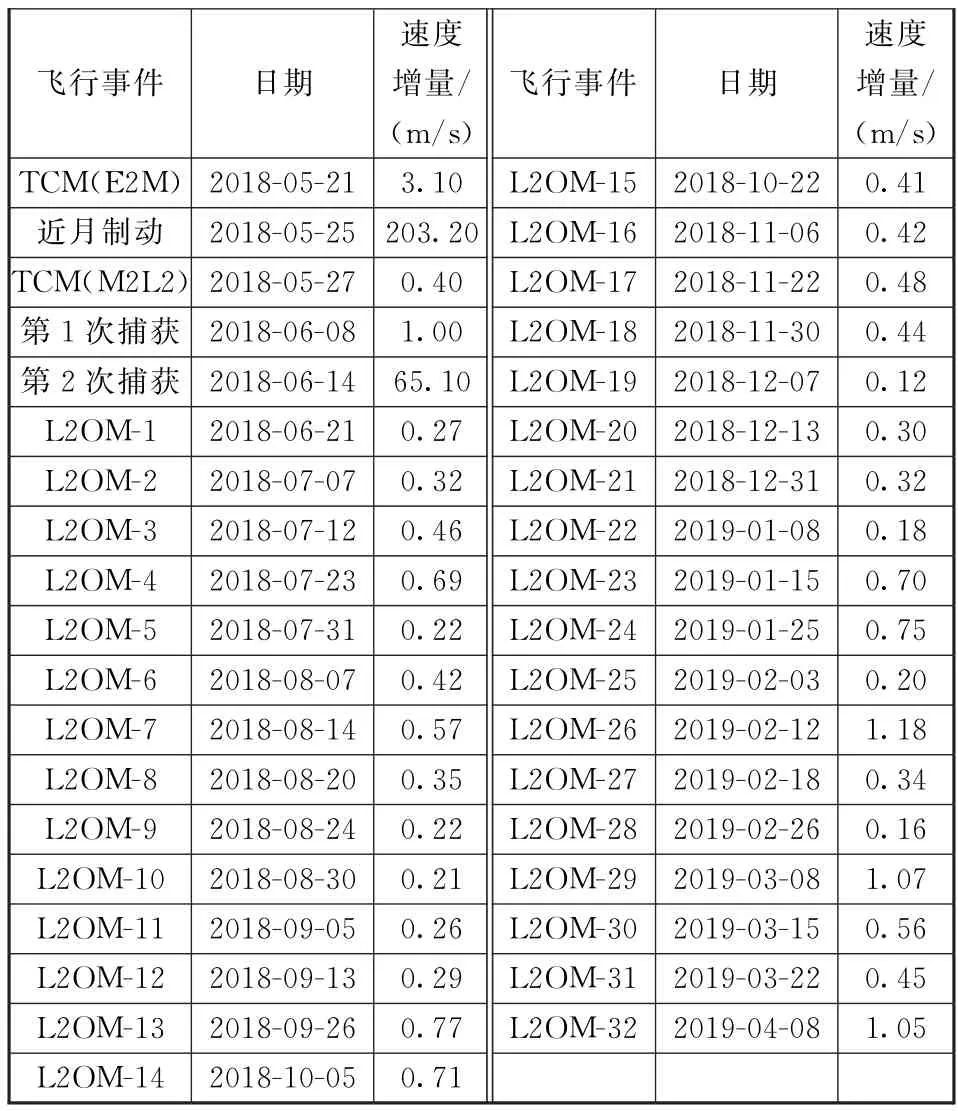
表5 軌道維持統計Table 5 Summary of orbit stationkeeping