晶振電路負載參數匹配與測試

孟永剛，陳浩，王軍

(聯創汽車電子有限公司,上海 201206)

0 引言

晶體振蕩器俗稱晶振，是晶振電路的核心元器件。晶振電路用于產生時間頻率基準，為微控制器系統(Microcontroller Unit，MCU)提供精準的時基。在實際應用中，如果晶振電路負載參數匹配不當，一方面，可能會造成晶振電路工作頻率出現偏差，進而造成計時不準，通信不能同步；另一方面，在睡眠喚醒時，電路擾動較小，可能會導致晶振電路起振困難。無論哪種情況，均會影響微控制器系統的性能甚至造成其無法工作。因此，合理匹配晶振電路負載參數具有十分重要的意義和實際應用價值[1-5]。

1 晶振電路原理

作為晶振電路的核心元器件，晶體振蕩器是一種能實現電能和機械能相互轉化的壓電器件，其等效電路如圖1所示，XTAL為晶體振蕩器；C0為等效并聯電容，其值與晶振的外形、尺寸有關；Lm為動態等效電感，代表晶振振動的慣性；Cm為動態等效電容，代表晶振的彈性；Rm為動態等效電阻，代表對電路的損耗。

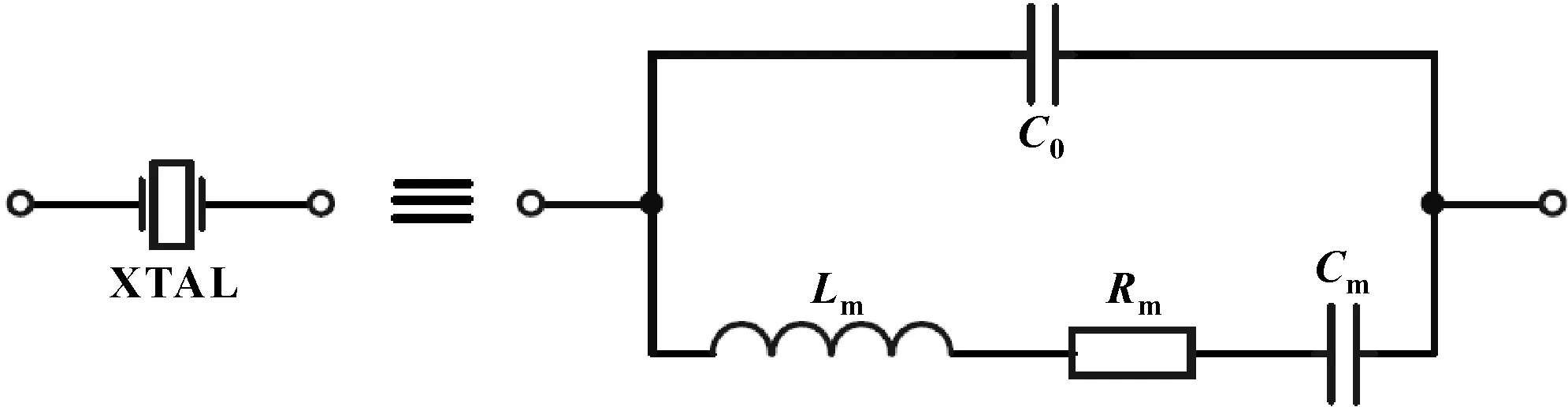
圖1 晶體振蕩器等效電路

晶振電路主要由一個放大器和選頻網絡組成，選頻網絡決定振蕩頻率。晶振電路在電能的作用下，放大了晶振工作頻率范圍內的擾動，從而造成起振。由于Pierce振蕩電路具有功耗低、成本低和穩定性高等優點，因此目前微控制器系統中使用的晶振電路多為Pierce振蕩電路[6]。Pierce振蕩電路原理圖如圖2所示。

圖2中，內部反相器的作用等同于放大器；RF為反饋電阻；RExt為限流電阻；CL1和CL2為外接負載電容；CS為等效雜散電容，CS是由芯片引腳、焊盤、封裝引腳和印刷電路板走線等引起的寄生電容。

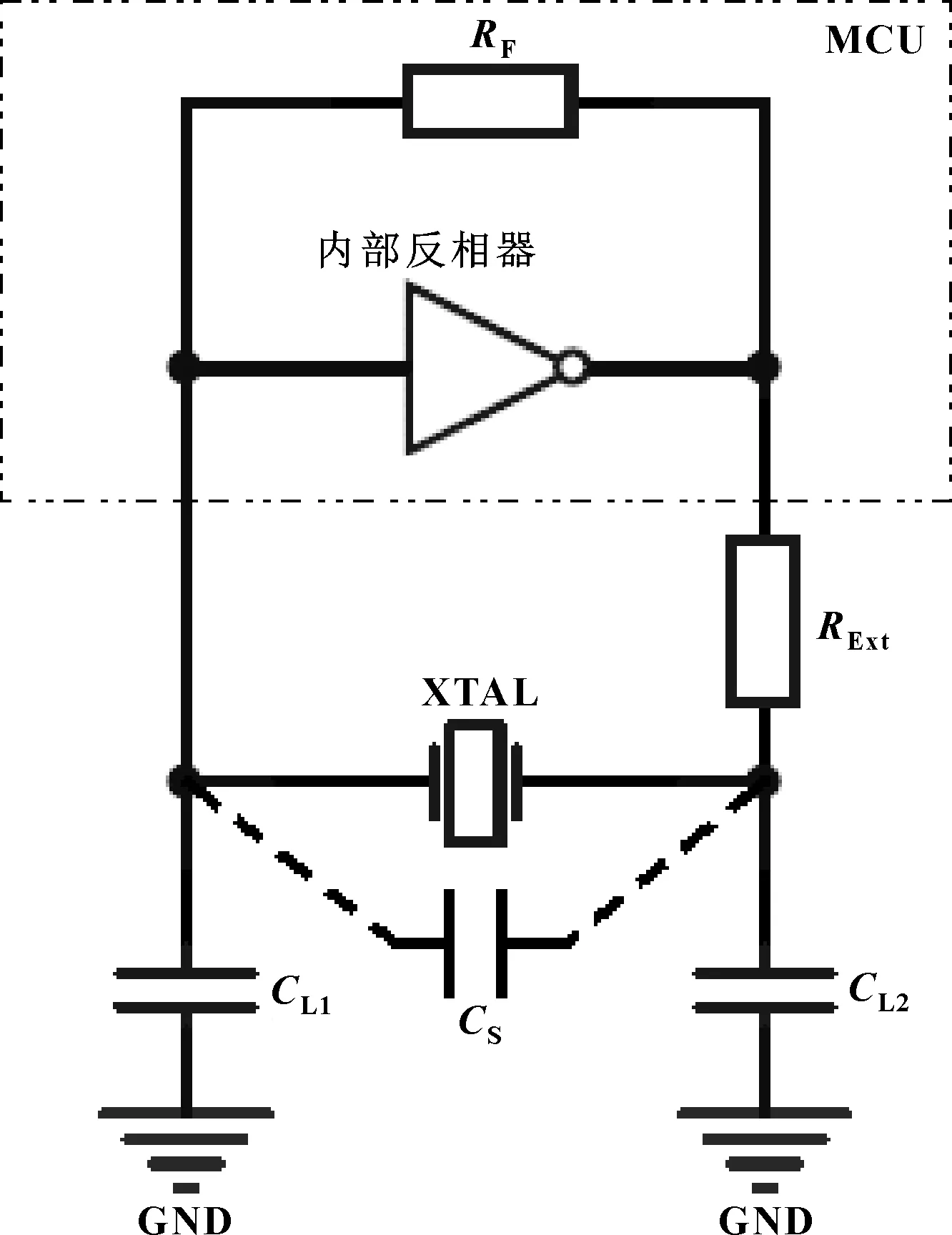
圖2 Pierce振蕩電路原理圖

2 晶振電路參數匹配

為了便于分析和說明，本文作者以某公司的一款電動助力轉向控制器(Electric Power Steering，EPS)中使用的Infineon SAK-TC264D-40F200W BB型號微控制單元所匹配的晶振電路為例進行晶振電路負載參數匹配介紹。選用的晶振型號為NX5032GA，其基本參數規格如表1所示。

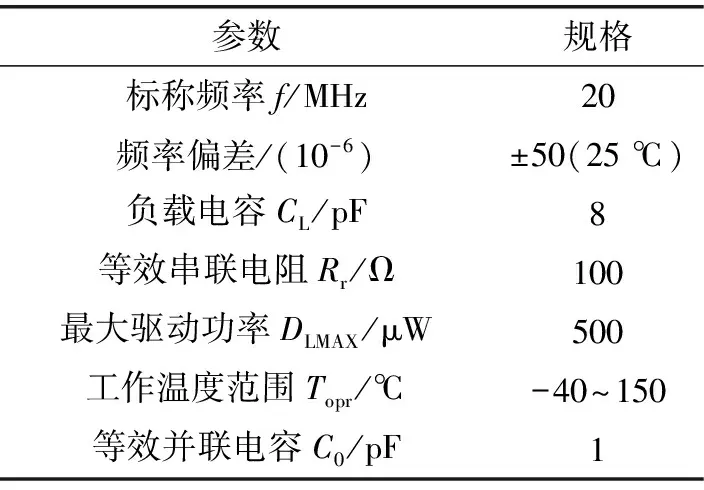
表1 晶振規格參數表

2.1 負載電容的計算與測試匹配

2.1.1 理論計算方法

負載電容CL的大小取決于外部電容CL1、CL2和等效雜散電容CS，計算公式如下：

(1)

晶振廠家在datasheet中通常會給出負載電容CL的標稱值。等效雜散電容CS與芯片引腳、焊盤、封裝引腳和印刷電路板走線等均有關系，無法得到具體理論數值，按照經驗，通常估算為3～5 pF[7]。一般兩個外部電容CL1和CL2選定為相同電容值。文中選定的晶振負載電容CL為8 pF，代入公式(1)可計算得到CL1=CL2=6～10 pF。

經過理論計算得到的外部電容CL1和CL2的范圍值可以作為后續測試匹配的參考，然后通過實際測試匹配實驗確定最優外部電容容值。

2.1.2 測試匹配方法

晶振的具體測試匹配方法是根據理論計算所得電容值范圍附近選取典型電容值的電容，然后分別測試并記錄不同外部電容值下的振蕩頻率、振蕩頻偏等參數，通過對比各參數選取最優外部電容值。

最優外部電容值評價準則：實測振蕩頻率越接近標稱振蕩頻率，振蕩頻偏越小，則電容值越優，實際測試匹配過程需要權衡選擇電容值。

2.1.3 測試匹配過程

晶振電路測試匹配的環境設置如圖3所示。此處測試的目的僅僅是為了進行不同負載參數下晶振特性的比對，驗證理論推算的正確性，因此文中選用示波器作為基本測量設備，如果需要獲取精度更高的頻率數據，需要選用專業的顯頻儀等設備進行測量。該實驗中選取6.8、8、10和100 pF 4種容值電容作為外部CL1和CL2的備選電容，限流電阻固定為1.5 kΩ，選擇100 pF電容是為了更明顯地驗證當外部電容值和理論計算值差別較大時的晶振輸出波形的表現狀況。通過更換不同容值的外部電容，并利用示波器采集晶振電路輸出波形(CL1和CL2需同時更換，保證CL1和CL2的容值始終一致)。對比輸出波形的穩定性、頻率偏差和幅值大小來判斷最佳容值。為了增加數據的可靠性，實驗中對每種工況波形隨機截取10次，利用10組隨機截取的實際波形頻率，以方差的方式計算每種工況的平均頻偏σ，平均頻偏σ定義如下：

(2)

式中：f0為晶振標稱工作頻率，文中為20 MHz，f1、f2、......、f10為10組隨機截取的晶振實際工作頻率。

圖3 晶振電路測試匹配環境設置

2.1.4 測試結果及分析

圖4給出了當外部電容為6.8、8、10及100 pF時，晶振電路的輸出波形。從圖中可以看出，在前3種外部電容配置下，晶振電路的輸出波形均較為平滑，未出現突變區域，波形重復度較高。當外部電容提升至100 pF時，可以看出，晶振電路輸出波形呈現出明顯不平滑現象，波形不規律區域較多。

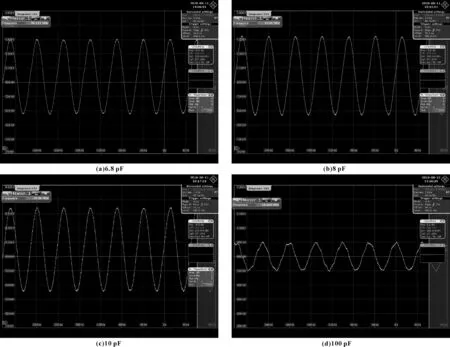
圖4 不同外部電容下晶振電路輸出波形

不同外部電容下晶振電路輸出波形的平均頻偏如圖5所示。

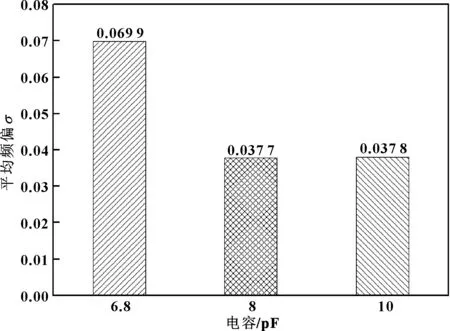
圖5 不同外部電容下晶振電路輸出波形的平均頻偏

圖5為當外部電容為6.8、8和10 pF時，晶振電路輸出波形的平均頻偏對比。可以看出，當外部電容為8和10 pF時，平均頻偏較低，且二者之間差別不大，當外部電容為6.8 pF時，平均頻偏明顯升高。說明8和10 pF是較為合適的容值。

2.2 限流電阻的計算與測試匹配

2.2.1 理論計算方法

外部限流電阻RExt的主要作用是限制反相器電流輸出的大小，控制晶振驅動功率，防止晶振驅動功率超過最大驅動功率限值而造成過驅動，進而導致晶振因為過度的機械振動而出現電極劣化、頻偏、壽命衰減等問題。外部限流電阻RExt的阻值通常是在確定了外部電容CL1、CL2的容值之后確定的。從晶振電路圖(圖2)中可以看出，限流電阻RExt和外部電容CL2構成分壓電路，在估算限流電阻RExt的電阻值時，通常是令RExt的電阻值和CL2的容抗值相等[8]，因此，RExt的估算公式如下：

(3)

當振蕩器頻率f0=20 MHz，CL2=10 pF，計算可得RExt為796 Ω。這個值僅僅是通過理論估算得到的，實際應用中并不一定能直接使用。因為實際應用晶振電路中，RExt需要做調整以調節流經晶振的電流大小，確保實際電路中的晶振驅動功率滿足廠家提供的指標要求。同時，RExt值也會影響晶振頻率偏差，頻率偏差過大也是不允許的。因此，必須通過實測的方法，改變RExt值，對比權衡參數指標的變化，進而確定最佳的限流電阻值。

2.2.2 測試匹配及結果分析

外部限流電阻的測試方法和過程與外部電容的測試基本一致，這里不再贅述。此處，選擇0.75、1.5、3和12 kΩ 4種電阻，外部電容固定為10 pF。不同電阻值匹配下的晶振電路輸出波形如圖6所示，對于前3種限流電阻，晶振電路輸出波形整體較為平滑，波形重復度較高，隨著阻值增加，波形幅值減小。而當限流電阻增加至12 kΩ時，晶振已無法正常起振。

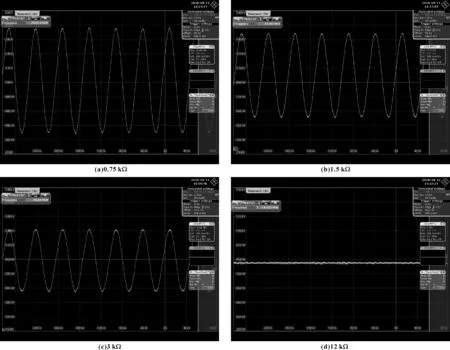
圖6 不同限流電阻下晶振電路輸出波形

圖7給出了當限流電阻為0.51、0.75、1.5和3 kΩ時，晶振電路輸出波形的平均頻偏對比。通過對比可以看出，當限流電阻為0.75 kΩ，即接近理論計算值0.796 kΩ時，平均頻偏最小，隨著電阻與理論計算值偏離的增加，平均頻偏逐漸增加。通過對比測試結果可以看到，在此實驗中所選的幾組電阻中，0.75 kΩ在滿足晶振驅動功率的前提下是最佳選擇。

2.3 負性阻抗的測試和計算

負性阻抗-R也稱為發振余裕度，用于評價晶振在發振回路上的發振能力。發振余裕度不足時，會導致振蕩電路振蕩不穩定甚至啟動失效等問題。負性阻抗-R需滿足-R>(5～10)Rr[7]，晶振電路才能穩定發振。晶振電路負性阻抗-R的測試電路原理圖如圖8所示。

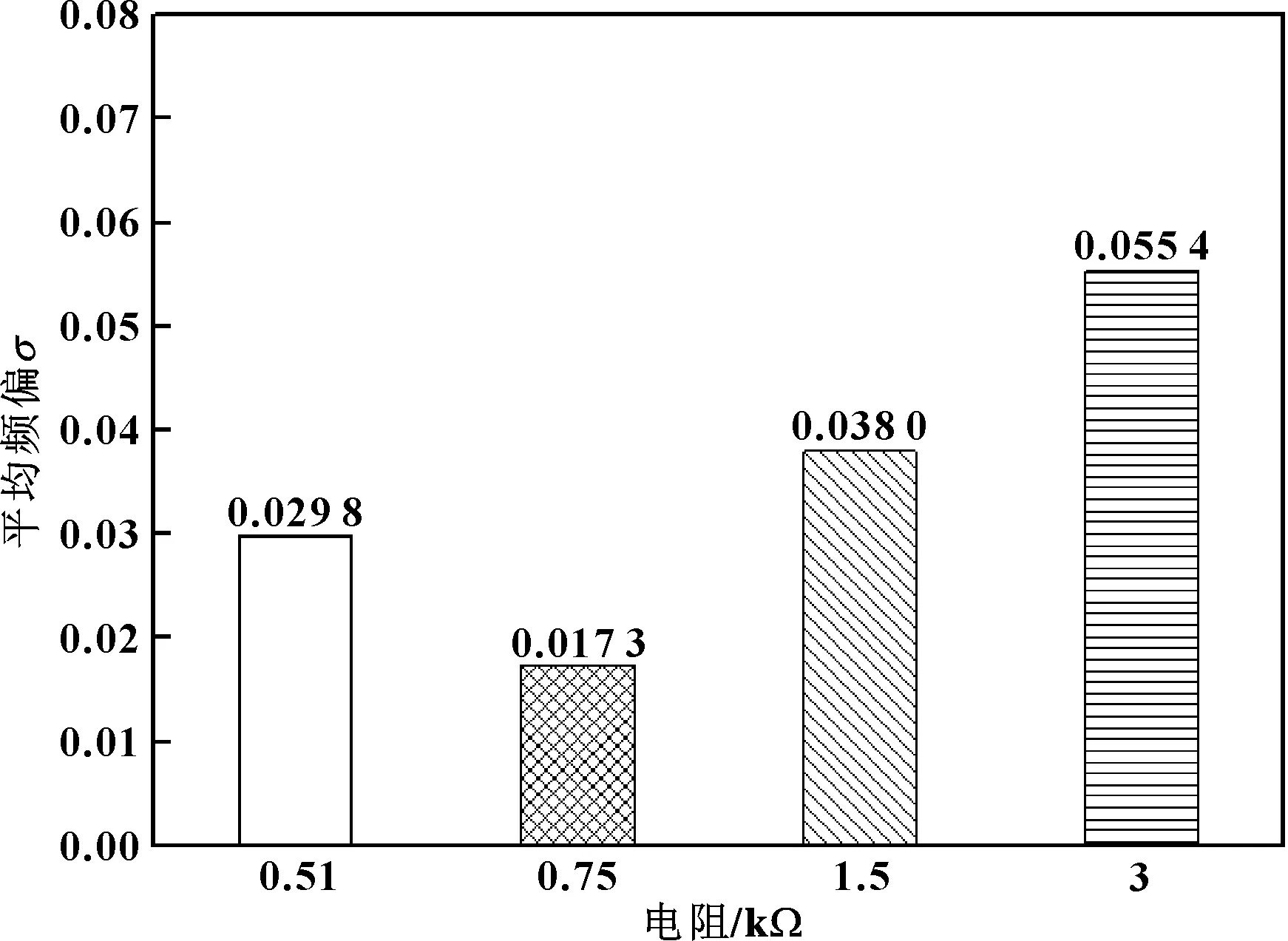
圖7 不同限流電阻下晶振電路輸出波形的平均頻偏

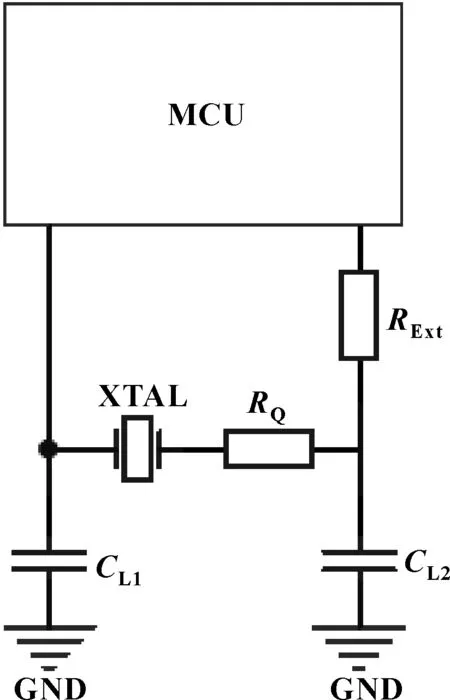
圖8 負性阻抗測試原理圖

圖8中RQ為可調電阻。具體測試方法：通過不斷增大RQ阻值，直到晶振停止振蕩，記錄此時的RQ阻值，根據測得的RQ值，可按如下公式計算負性阻抗：

-R=RQ+RL

(4)

(5)

式中：RL為加載后的諧振電阻；Rr為等效串聯電阻。文中設計的晶振電路經過測量計算得到的負性阻抗-R為1 330 Ω，-R>10Rr=10×100 Ω=1 000 Ω，因此，該晶振電路滿足晶振起振和穩定工作條件。

2.4 驅動功率的測試與計算

晶振驅動功率DL不能超過晶振制造商給出的最大驅動功率DLMAX，否則晶振會因為過度地機械振動而出現電極劣化、頻偏、壽命衰減等問題。驅動功率DL計算公式如下：

(6)

式中：IQ是流過晶振電流的均方根有效值，電流有效值IQ的計算公式為

(7)

式中：IPP為正弦波電流峰-峰值。綜上所述，驅動功率DL的計算公式：

(8)

經過測試計算，文中晶振電路的晶振驅動功率DL為90 μW，而DLMAX為500 μW，DL

3 結束語

結合一款應用于電動助力轉向系統中的微控制器單元所匹配的晶振電路，對晶振電路負載參數的理論計算、測試和匹配方法進行了介紹。可以看出，通過測量匹配的負載參數與理論計算匹配得到的晶振電路負載參數基本吻合。在實際應用中，不同的MCU、不同的PCB布線方式、不同的環境條件均會對晶振電路負載參數產生影響。因此，在設計晶振電路和進行晶振電路負載參數匹配時，需以理論計算方法為參考，結合測試手段，權衡匹配出最適合當前控制器電路環境的負載參數，使設計的晶振電路工作在最佳狀態。