非標準有限差分法求解薛定諤方程
劉明鼎, 林 鑫, 張艷敏
(青島理工大學琴島學院 基礎部, 山東 青島 266106)
薛定諤方程是物理領域量子力學的一個重要方程.可以用來討論單色波的一維自調適、光學的自陷現象、固體中的熱脈沖傳播、等離子體中的Langnui 波、超導電子在電磁場中運動以及激光中原子的Bose-Einstein凝聚效應等[1-3],也被用于研究深水波浪理論、柱(球)非線性薛定諤方程[4-5],因此研究此類方程具有重要的意義.本文結合構造非標準有限差分格式的特點[6-8],給出求解薛定諤方程的一種非標準有限差分格式.通過分析,證明了構造的差分格式是無條件穩定和收斂的.數值算例驗證了該方法是有效的.
1 兩種非標準有限差分格式的構造
考慮如下初邊值薛定諤方程:
初始條件
u(x,0)=φ(x),0≤x≤L,(2)
邊界條件
u(0,t)=φ0(t),u(L,t)=φ1(t),0 這里i為虛數單位,f,φ,φ0,φ1為已知連續函數,L,T為非負常數. 利用MICKENS方法[6],以及文獻[9-11]在網格點處對式(1)離散后的差分方程為 對式(5)進一步整理 則式(6)即為式(1)第一種非標準有限差分格式. 定義差分符號 其中,分母函數D1、D2與式(4)所對應的分母函數相同.對式(7)進行整理得 則式(8)即為式(1)第二種非標準有限差分格式. 利用標準的有限差分方法構造的顯示有限差分格式為 考慮如下初邊值問題: 表1 數值解誤差Table 1 Error of numerical solution 續表1 (x,t)精確解實部虛部格式一誤差實部虛部格式二誤差實部虛部標準差分格式誤差實部虛部(0.6,1.0)0.984491.533264.125×10-45.891×10-46.102×10-47.048×10-48.698×10-47.162×10-4(0.7,1.0)1.088041.694513.266×10-54.125×10-53.000×10-54.059×10-58.123×10-38.168×10-4(0.8,1.0)1.202461.872733.200×10-43.128×10-44.159×10-42.618×10-45.136×10-45.126×10-3(0.9,1.0)1.328932.069682.981×10-45.269×10-42.782×10-42.998×10-43.025×10-36.024×10-4 非標準有限差分格式的構造需要考慮偏微分方程解的特征.非標準格式在保持原偏微分方程的性質方面比傳統的差分格式更有效[11-13].目前還沒有研究薛定諤方程的精確差分格式的相關文獻.在接下來的工作中,將利用文獻[6-7]的方法討論深水波浪非線性薛定諤方程的精確有限差分格式.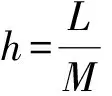
1.1 第一種非標準有限差分格式的構造
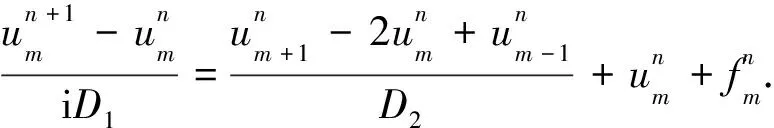
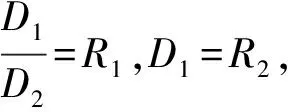
1.2 第一種非標準有限差分格式的局部截斷誤差


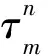

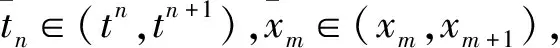
1.3 第二種非標準有限差分格式的構造

1.4 第二種非標準有限差分格式的局部截斷誤差
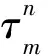


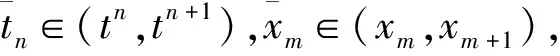
1.5 標準有限差分格式
2 數值算例
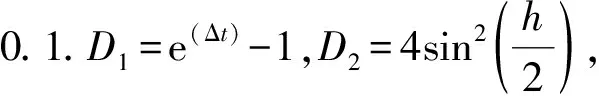


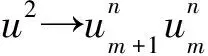
3 結 論

