多因素影響下巷道變形特性數值模擬研究*

黃 鑫，姚韋靖

(安徽理工大學 土木建筑學院，安徽 淮南 232001)

0 引言

我國煤炭賦存量的73.19%位于距地表600 m以下的深部，隨著煤炭需求量的日益增加，國內礦山開始陸續進入深部開采階段，深部開采帶來的一系列難題也逐漸顯現[1-5]。進入深部開采后，圍巖在面對“三高一擾動”的復雜力學條件下，巷道的破壞規律與變形控制成為眾多學者研究的重點之一[6-10]。

針對巷道變形因素進行研究對于深部巷道支護具有重要意義，何富連等[11]研究發現巷道側壓力系數對于底板穩定性影響顯著，當側壓力系數大于1.5時，底板塑性區范圍急劇擴大，為此提出了巷幫大直徑鉆孔卸壓的方法抑制變形；孟慶彬、李桂臣等[12-13]認為巷道形狀是影響巷道變形的重要因素，提出“等效開挖理念”，認為曲線形巷道的穩定性、塑性區范圍、變形性能均優于直線型巷道；高富強等[14]利用數值模擬的方法，采用矢跨比定義巷道斷面形狀，得出圓弧拱巷道的穩定性要優于矩形巷道；姜增國等[15]利用數學的方法，提出了巷道斷面最佳選擇方法——模糊決策法；Wang等[16]針對長期處于高應力狀態下的巷道圍巖變形趨勢進行研究，提出適用于軟巖巷道的U型鋼支撐與錨注聯合支護技術；張明[17]研究了圍巖性質、巷道埋深、巖層傾角、支護方式等因素對巷道變形的影響；陳登紅等[18]研究了巷道埋深、斷面形狀等對巷道穩定性的影響，并提出了“掘進優化、強幫護頂、分區控頂”等巷道圍巖控制的原則；張立新等[19]針對軟巖巷道變形因素進行了研究，發現孔隙水壓力對其影響規律與應力場的分布相同。以上研究均針對某一或兩個因素逐個展開了具體研究，且判斷巷道失穩的指標較為單一，本文總結前人成果，采用正交試驗的方法，借助FLAC3D有限差分軟件綜合開挖深度、側壓力系數以及巷道斷面形狀3種因素，采用塑性區、應力值2種不同指標描述巷道變形的特征，根據模擬結果分析得出了巷道斷面形狀與塑性區分布的規律和開挖深度與應力值之間的關系，為深部巷道設計優化提供借鑒和參考。

1 試驗設計

1.1 數值模擬模型與參數確定

利用FLAC3D軟件建立1個50 m×50 m×50 m的立方體模擬區域，在其正面對角線交點處分別開挖直墻半圓拱形、圓形、矩形以及馬蹄形巷道，具體巷道斷面尺寸見圖1。以淮南礦業集團張集煤礦第二副井主排水硐室為工程背景，根據工程實際情況建立模型，如圖2所示。

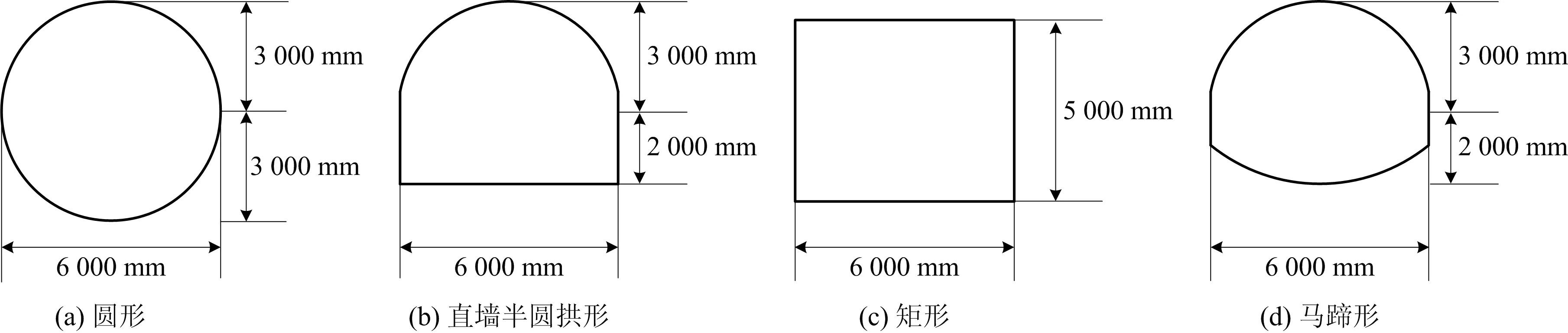
圖1 巷道斷面尺寸Fig.1 Roadway section size

圖2 數值模擬三維模型Fig.2 Numerical simulation of three-dimensional model

本模型限制其底部和側向位移，根據深度和側壓力系數的不同在其上表面和左右2個側面施加相應的應力，不同圍巖的力學參數如表1所示；模型采用Mohr-Coulomb準則，開挖前進行地應力平衡，待應力和位移曲線呈水平分布后，沿巷道縱軸線方向，分別以拱頂和底板中心為起點，布置2條長度為22 m的監測線，沿垂直于縱軸線方向，以巷道邊墻為起點，分別布置2條長度為22 m的對稱監測線，測線布置如圖3所示，監測開挖后拱頂、底板以及邊墻兩側的收斂量變化。

1.2 正交試驗設計

為保證結果分析科學有效，采用正交試驗法來設計試驗，本次試驗共有3個影響因素，分別為：開挖深度(A)、側壓力系數(B)和斷面形狀(C)，其中，地應力情況以開挖深度來表示，圍巖結構特征以側壓力系數λ來表示。每個影響因素設計4個水平，根據正交表L1645設計試驗，試驗方案見表2。

2 試驗結果及分析

從塑性區范圍、應力值大小2個方面來描述巷道變形的程度，以塑性區深度和(巷道頂板、底板、兩幫最大塑性區深度和)、應力差(最大應力與最小應力差)2個指標作為正交試驗結果判定的指標，正交試驗結果見表3。

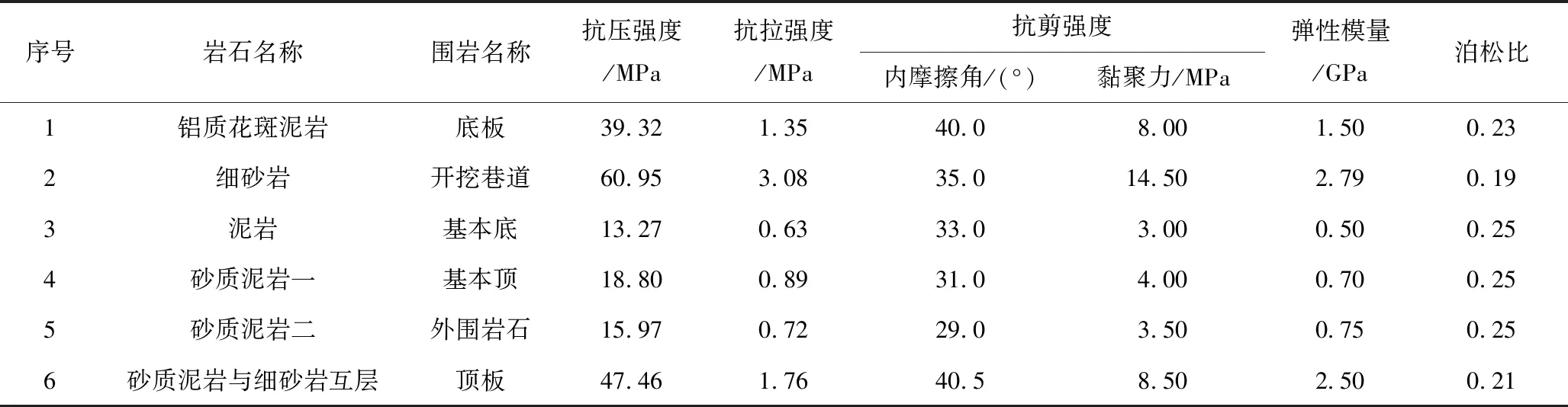
表1 巷道圍巖力學參數Table 1 Roadway surrounding rock mechanics parameters

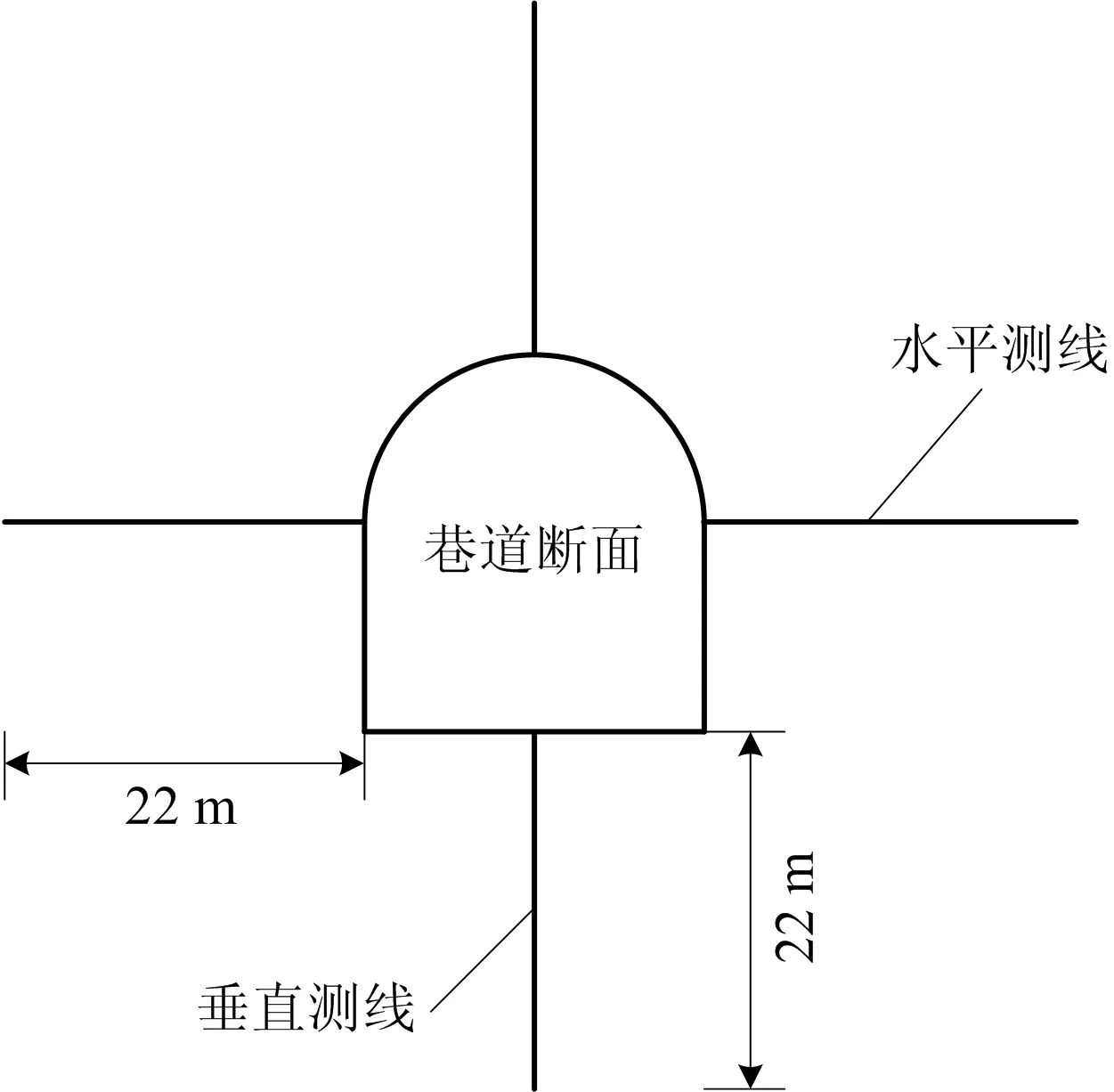
圖3 測線布置Fig.3 Line layout

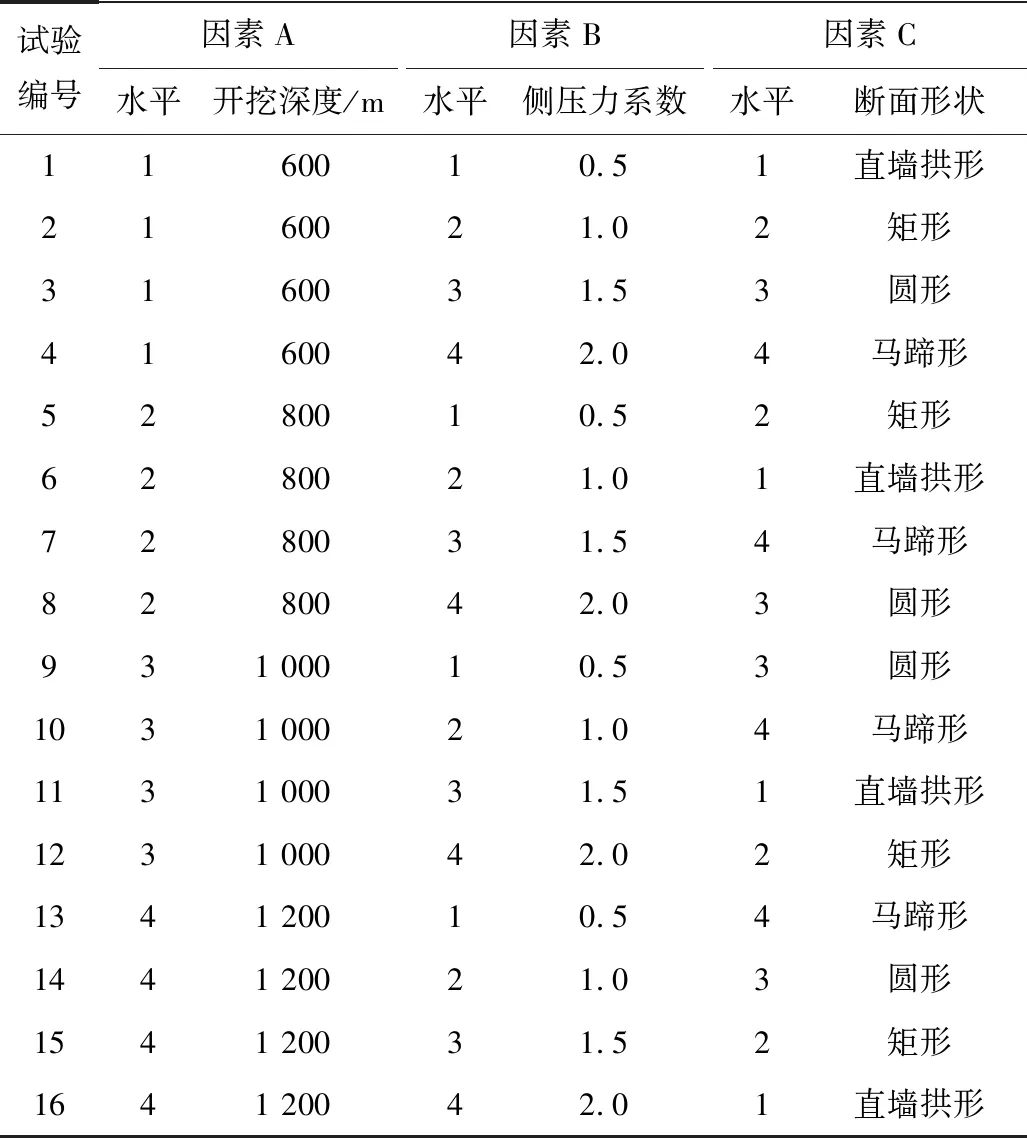
試驗編號因素A因素B因素C水平開挖深度/m水平側壓力系數水平斷面形狀1160010.51直墻拱形2160021.02矩形3160031.53圓形4160042.04馬蹄形5280010.52矩形6280021.01直墻拱形7280031.54馬蹄形8280042.03圓形931 00010.53圓形1031 00021.04馬蹄形1131 00031.51直墻拱形1231 00042.02矩形1341 20010.54馬蹄形1441 20021.03圓形1541 20031.52矩形1641 20042.01直墻拱形

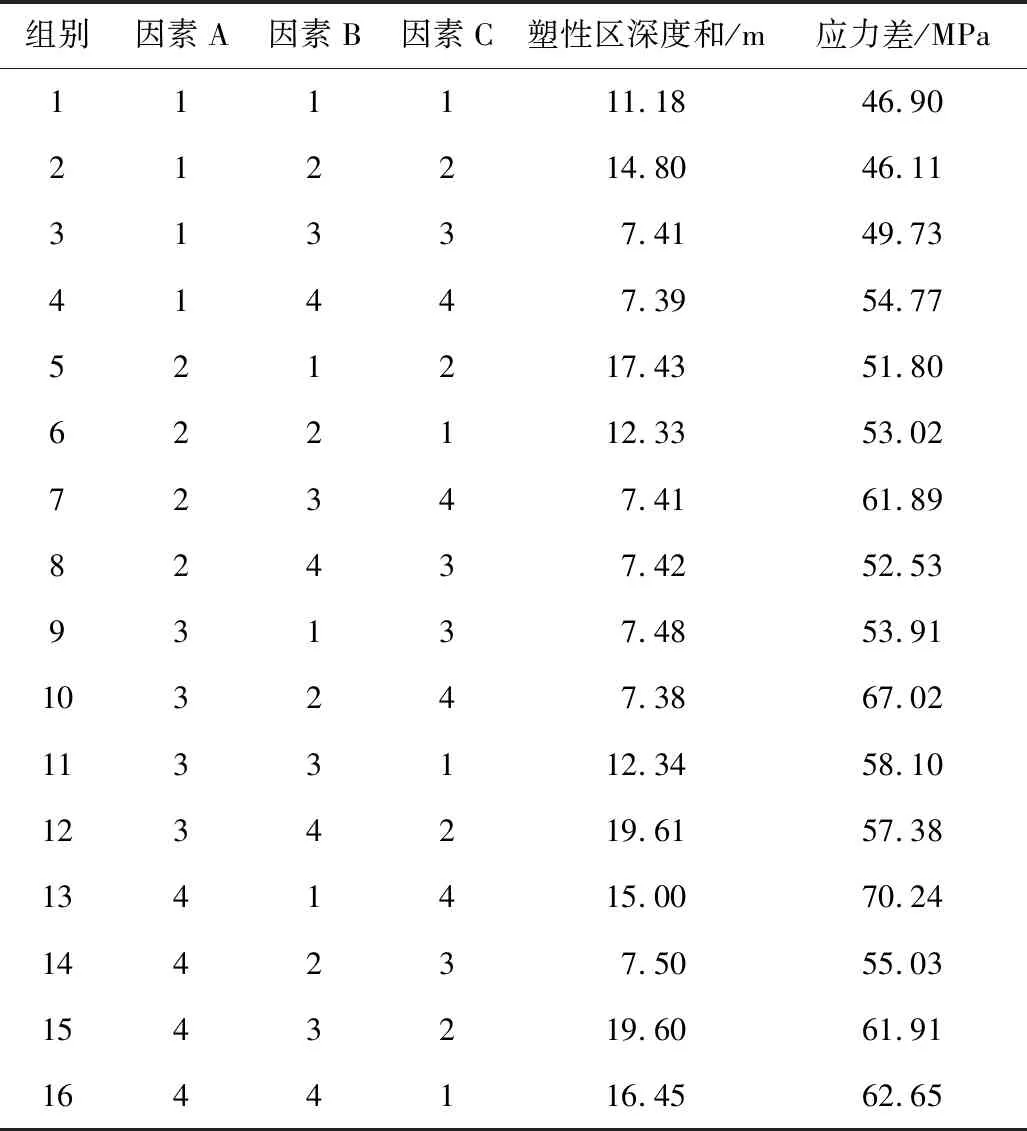
表3 正交試驗結果Table 3 Orthogonal test results

根據表3的試驗結果對其進行方差分析，各因素對指標的影響情況如表4所示。

由表4可知，對塑性區深度和，各因素影響順序為：斷面形狀>開挖深度>側壓力系數；對應力差，各因素影響順序為：開挖深度>斷面形狀>側壓力系數。綜上可知，開挖深度對巷道內的應力變化具有較大的影響，而斷面形狀對應巷道開挖后塑性區的分布特征起到了關鍵性的作用。因此針對斷面形狀及開挖深度對巷道變形的影響規律進行模擬研究。

3 斷面形狀對巷道變形的影響

為更好的描述斷面形狀對巷道變形程度的影響，引入斷面形狀特征的形狀指數[20]，描述斷面形狀的周長與面積之間的關系，以便于準確描述不同斷面的特征；圓形可看作無窮多邊形，故以圓形為基準，設圓形的形狀指數為1。根據圓的周長公式和面積公式可得形狀指數：

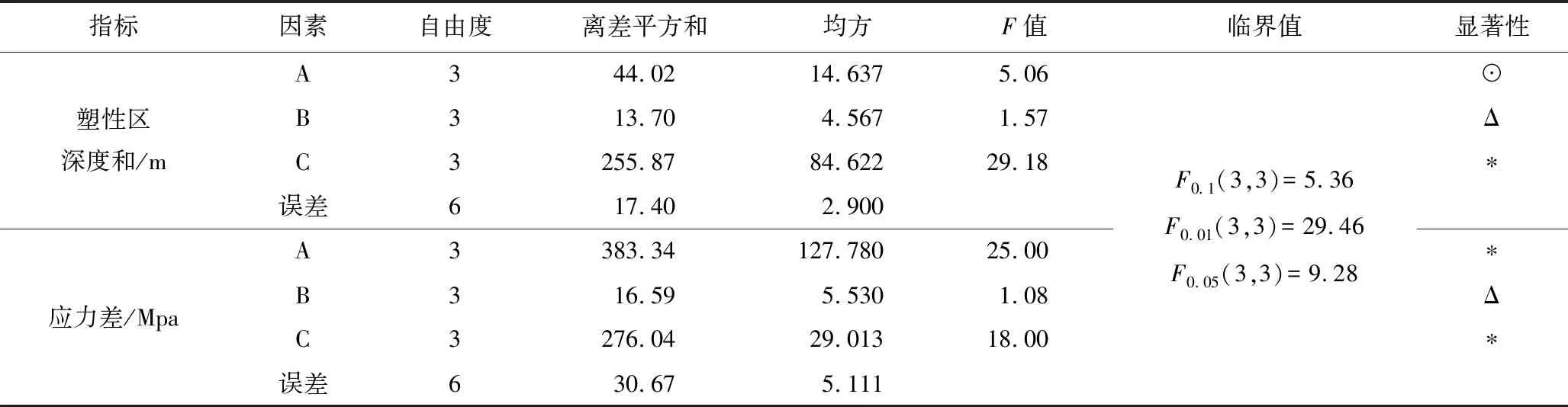
表4 方差分析結果Table 4 Variance analysis results

注：**為高度顯著；*為顯著；⊙為有影響；Δ為有一定影響。

SD=1=P/A

(1)

則有：

(2)

式中：P為斷面周長，m；A為斷面面積，m2。

不同形狀正多邊形的形狀指數如表5所示。

表5 形狀指數Table 5 Shape index

根據不同邊數的凸多邊形形狀指數繪制形狀變化趨勢圖(見圖4)可以看出，隨著邊數的增加，其形狀指數的變化趨勢呈現下降趨勢，且下降速率逐漸減緩，并趨于1，當多邊形取得邊數趨于無窮多時，其效果近似于圓形，形狀指數達到1。

選取開挖深度為1 000 m，側壓力系數為1時，探究不同斷面形狀對巷道開挖后塑性區分布的影響規律，塑性區分布情況如圖5所示。

由圖5可知，圓形巷道和馬蹄形巷道的塑性區分布在巷道兩幫，主要以剪切破壞為主，圓形巷道開挖完成后仍存在的剪應力塑性區集中在兩幫中部及下部，馬蹄形巷道開挖完成后仍存在的剪應力塑性區集中在兩幫中部及上部；直墻拱形巷道的拱形部分的塑性區分布與圓形巷道類似，以剪應力破壞為主，其底板以拉應力破壞為主，底板與兩幫交界處的直角區域內塑性區深度達到最大并以剪切破壞為主，表明尖銳的角度易造成應力集中，導致塑性區范圍加大；矩形巷道兩幫塑性區以剪應力為主，頂板和底板塑性區主要以拉應力為主，同時，矩形巷道4個直角的塑性區分布呈矩形對角線向外延伸，塑性區深度大于兩幫、頂板和底板塑性區的深度。

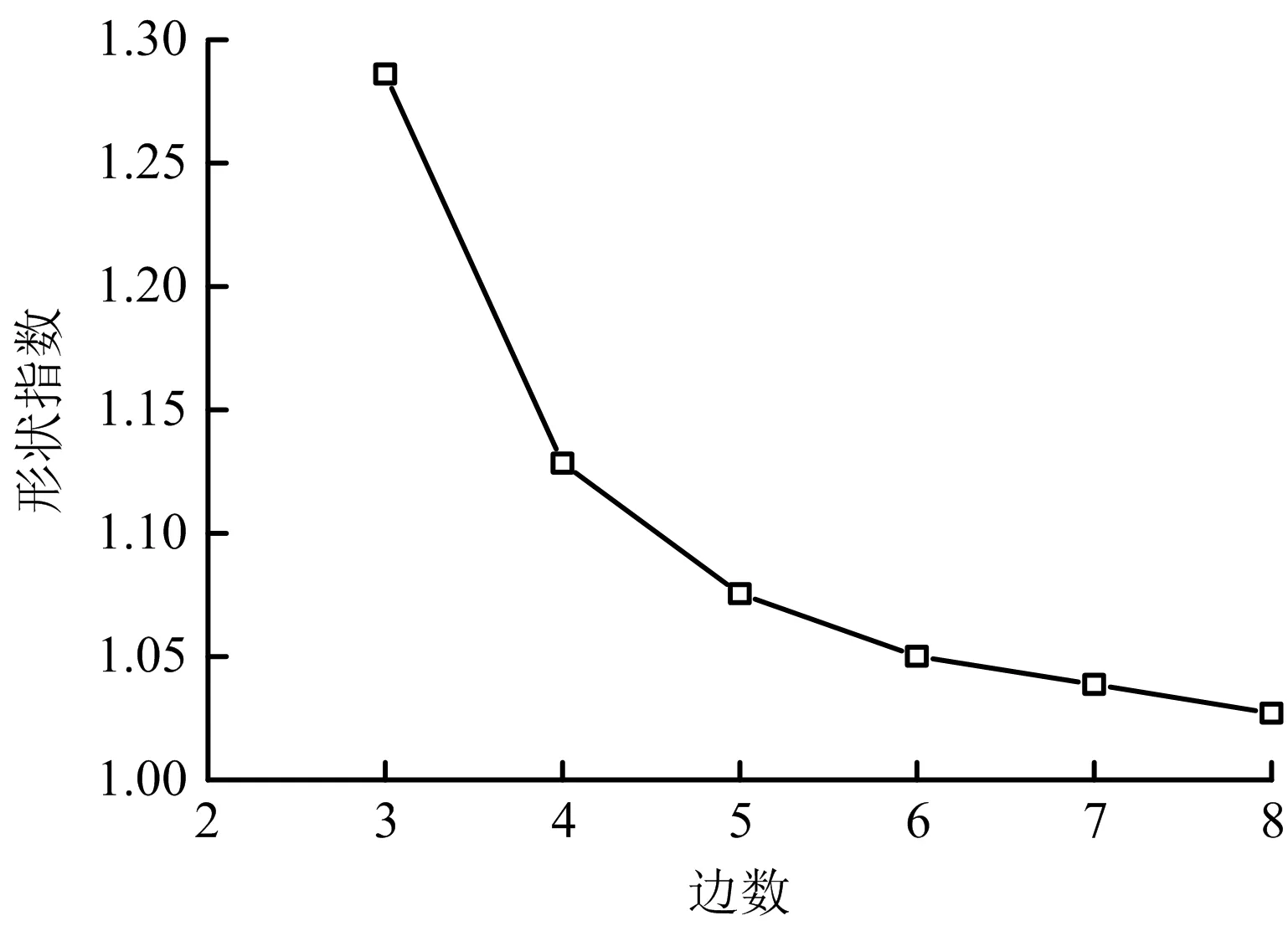
圖4 形狀變化趨勢Fig.4 Shape change trend

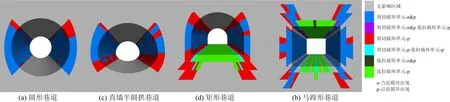
圖5 各斷面形狀巷道塑性區分布Fig.5 Plastic zone distribution of roadway in each section shape

根據式(2)計算各斷面形狀指數以及塑性區深度和(見表6)，根據表6數據繪制斷面形狀指數與塑性區深度和之間的關系曲線，R2為擬合方差，如圖6所示。

表6 各斷面形狀的形狀指數與塑性區深度和Table 6 Relationship between shape index and depth of plastic zone

由圖6可知，形狀指數與塑性區深度和基本呈線性關系，用一階線性函數y=67.29SD-60.211可以很好的描述二者之間的關系，隨著形狀指數的減小，巷道開挖后的塑性區范圍逐漸減小，即巷道斷面越接近圓形，斷面形狀越“圓滑”，其塑性區范圍越小，相對于有尖銳轉角斷面的巷道擁有更好的穩定性。

圖6 形狀指數與塑性區深度和關系曲線Fig.6 Shape index and plastic zone depth and relationship curve

4 開挖深度對巷道圍巖內應力差的影響

根據分析可知，圓形巷道和馬蹄形巷道具有較好的穩定性。以圓形巷道為例，探究其在開挖深度為600，800 ，1 000和1 200 m時，巷道圍巖內的應力分布、頂底板變形量的變化規律，如圖7所示。

圖7 圓形巷道在不同深度的應力分布Fig.7 Stress cloud map of circular roadway at different depths

由圖7可知，圓形巷道開挖后的最大應力主要集中在兩幫處，最小應力集中在拱頂和底板中心，且最大和最小應力均隨開挖深度的增加而增加，當開挖深度由600 m增加至800 m時，最小應力增加15.4%，增長幅度變化最大，當開挖深度1 000 m增至1 200 m時，最大應力增長9.4%，增長幅度最大。這表明巷道隨開挖深度的增加，承受的應力越來越大，使得巷道變形愈加嚴重，隨著應力的增加會導致巷道出現擠壓變形，應力分布不均會導致巷道出現剪切應力導致巷道內壁開裂甚至坍塌。

根據圓形巷道在不同深度的應力分布特征，繪制巷道應力變化趨勢圖，如圖8所示。

圖8 圓形巷道應力變化趨勢Fig.8 Circular roadway stress change

由圖8可知，最大應力與最小應力均表現為隨深度增加而增長的趨勢，其應力差值也逐漸增大，由600 m深度時的61.52 MPa增長至1 200 m深度時的74.39 MPa，增長率達到20.9%，其中深度由600 m至800 m，應力差值增長6.6 %，由800 m至1 000 m，應力差值增長4.4%，由1 000 m至1 200 m，應力差值增長9.2%，增長率大于此前2個階段。由此可見，隨著開挖深度的增加，巷道穩定性不僅面臨著高應力的危害，還將受到高應力分布差的影響，較高的應力差值會使巷道穩定性降低，支護難度加大，會在巷道兩幫出現較大的剪切力，巷道頂板和底板出現較大的拉伸力，加速巷道變形，危害極大。

5 結論

1)根據正交試驗方差分析可知，斷面形狀對巷道開挖后的塑性區深度和影響較大，開挖深度對巷道開挖后的應力差具有顯著影響，側壓力系數對正交試驗的2個指標影響較小。

2)針對巷道斷面影響特點引入形狀指數，巷道開挖后的塑性區深度和隨形狀指數增加而呈線性增長趨勢，圓形巷道的塑性區深度和最小，矩形最大。

3)巷道開挖后的應力差隨開挖深度的增加而增加，其中，1 000 m至1 200 m階段,增長趨勢明顯加快，對于深部開采更應重視巷道內應力分布的情況，防止出現應力分布不均導致的剪切或拉伸破壞。