不同樓梯布局條件下行人疏散效果仿真研究*

李若菲，趙永翔，盧團團，劉旭光

(福州大學(xué) 經(jīng)濟與管理系，福建 福州 350116)

0 引言

近年來，建筑火災(zāi)造成的人員傷亡事件屢有發(fā)生，尤其對于人員密集、火災(zāi)荷載大的場所，一旦發(fā)生火災(zāi)極易造成重大人員傷亡和財產(chǎn)損失，甚至造成惡劣的社會影響[1]。樓梯是各種建筑物中的主要疏散環(huán)節(jié)，特別是一些大型的人群聚集場所，如火車站、地鐵站、商業(yè)廣場、教學(xué)樓等。在緊急事件發(fā)生時(如停電、火災(zāi)、地震等)，樓梯也是主要的逃生通道。而樓梯疏散在疏散速度、步幅寬度、人員間相互影響等方面都不同于平面上的疏散[2]。因此，針對樓梯區(qū)域人員疏散特征進行研究具有重要的現(xiàn)實意義。

對于人員疏散問題，常使用的行人模型主要是社會力模型[3]、元胞自動機模型[4]及格子氣模型[5]等。其中，Helbing等[3]提出的社會力模型是研究行人流領(lǐng)域的空間連續(xù)模型，以分析行人間的物理力和心理作用力為主，能夠復(fù)現(xiàn)一些自組織現(xiàn)象，如成拱現(xiàn)象等。目前許多學(xué)者使用該模型對樓梯上的行人流進行仿真研究。Seyfried等[6]用改進的社會力模型研究樓梯區(qū)域行人運動特性，并分析樓梯尺寸、臺階的限制以及速度的影響等；Wu等[7]結(jié)合行人自身重力因素改進了社會力模型，來研究狹窄的樓梯空間中行人的運動特性；李娟等[8]基于傳統(tǒng)社會力模型，引入重力分力和邊界吸引力來描述行人在階梯路段的運動特征。但這些研究大多為二維空間的模擬，忽略了豎直方向上的運動。

現(xiàn)實生活中，不同布局的行人交通設(shè)施有不同的通行能力，而不合理的設(shè)計會導(dǎo)致交通擁堵，影響行人的正常行走，合理的設(shè)計則能提高交通設(shè)施的通行能力，緩解行人擁擠并節(jié)約資源。Mona Afifi等[9]研究了對老年人安全友好的樓梯布局，提出基于證據(jù)的評估方法來評估樓梯元素，并結(jié)合數(shù)學(xué)模型與設(shè)計評估樹的場景評級系統(tǒng)預(yù)測不同類型的建筑樓梯設(shè)計的跌落風(fēng)險程度；丁元春等[10]和郭曉明等[11]利用Pathfinder仿真平臺研究了高層建筑中2種樓梯布局下的行人疏散效果，并對比分析了宏觀上的疏散指標(biāo)，即總疏散時間和平均疏散速度。但目前鮮有關(guān)于不同樓梯布局條件下行人疏散行為的宏微觀特征的對比分析。

本文擬從三維視角，用改進的社會力模型對4種常見樓梯布局下(即單跑有平臺梯形，單跑無平臺梯形，雙跑梯形及雙分梯形)的行人疏散特征進行宏微觀對比分析。并按以下研究思路開展工作：首先對傳統(tǒng)社會力模型進行改進；然后對4種常見的樓梯布局進行模擬分析；最后，通過分析總疏散時間、平均疏散速度及速度及密度分布圖來探討這4種常見樓梯布局的疏散效果，以期為建筑中的樓梯布局選擇、設(shè)計及規(guī)劃提供一定的參考依據(jù)。

1 三維SFM構(gòu)建

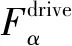
(1)

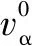
(2)

其中：行人α的空間位置sα(t)的變化可由vα(t)=dsα/dt來計算。

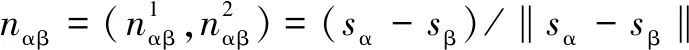
因此，行人α，β的作用力可以根據(jù)方程定義為：

(3)

當(dāng)行人之間并未接觸時，函數(shù)g(x)=0，否則為復(fù)數(shù)x。

類似的，與墻壁w的作用力也可以通過方程得到：

(4)

式中：dαw表示到墻壁w的距離;nαw表示垂直與墻壁的單位向量;tαw表示正切于墻壁的方向。

行人上下樓梯的過程是1個典型的三維運動，不僅包括水平(x-y平面)方向上的運動，還包括垂直(z軸)方向上的運動。因此，在傳統(tǒng)的二維社會力模型的基礎(chǔ)上，考慮垂直方向上的運動，構(gòu)建三維(x-y-z)社會力模型。

三維樓梯運動速度分解示意如圖1所示。行人的實際速度vα可以被分解為vx，vy以及vz，即

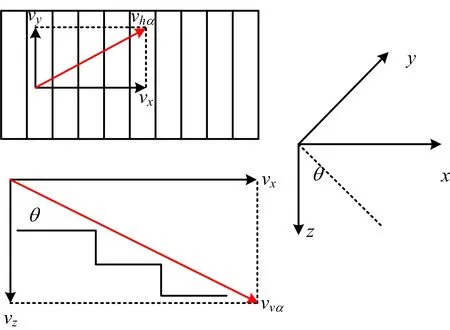
圖1 樓梯運動速度分解示意Fig.1 Diagram of stair movement speed decomposition

(5)

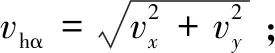
根據(jù)實驗觀察，行人在樓梯上運動時，豎直方向上的速度vz依賴于水平方向上的速度vx，即

vz=vxtanθ

(6)

式中：θ指樓梯的坡度。當(dāng)行人在臺階上行走時，θ為樓梯實際坡度值；當(dāng)行人在中間平臺等平坦區(qū)域運動時，θ被設(shè)為0。

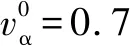
2 4種常見梯形下行人疏散仿真及分析

2.1 4種常見梯形示意圖

根據(jù)調(diào)查發(fā)現(xiàn)，建筑場所中常使用的樓梯類型為單跑有平臺、單跑無平臺、雙分及雙跑。這4種梯形的定義見文獻[12]，即單跑無平臺：上下樓層只有1個樓梯梯段由上而下；單跑有平臺：在無平臺基礎(chǔ)中間設(shè)有1個平臺；雙跑：上、下樓層之間設(shè)有2個樓梯梯段，梯段在平面位置上互相平行，梯段之間通過樓梯平臺連接；雙分：包含3個梯段，第1梯段位于樓梯間中部位置，第2和第3梯段則分別位于第1梯段兩側(cè)，第2，3梯段的寬度均為第1梯段的1/2，中間通過樓梯平臺連接(圖2)。

圖2 4種梯形示意Fig.2 Schematic view on the staircase configurations

2.2 仿真樓梯參數(shù)設(shè)置

對這4種樓梯布局的行人疏散過程分別進行模擬。建筑仿真模型的區(qū)別僅在于樓梯梯形不同，即假定在限定空間中，4種樓梯都是兩層高，單個樓梯段豎直高度為2.72 m，每段樓梯含16個臺階(單跑無平臺樓梯一共32個臺階)，每個臺階高0.17 m、深0.33 m，坡度為27.3°。筆者通過實際測量學(xué)校教學(xué)區(qū)樓梯尺寸來設(shè)置參數(shù)，且符合《民用建筑設(shè)計通則》和《建筑樓梯模數(shù)協(xié)調(diào)標(biāo)準(zhǔn)》。臺階參數(shù)和4種梯形平面示意如圖3所示(箭頭和序號表示行人運動方向)。

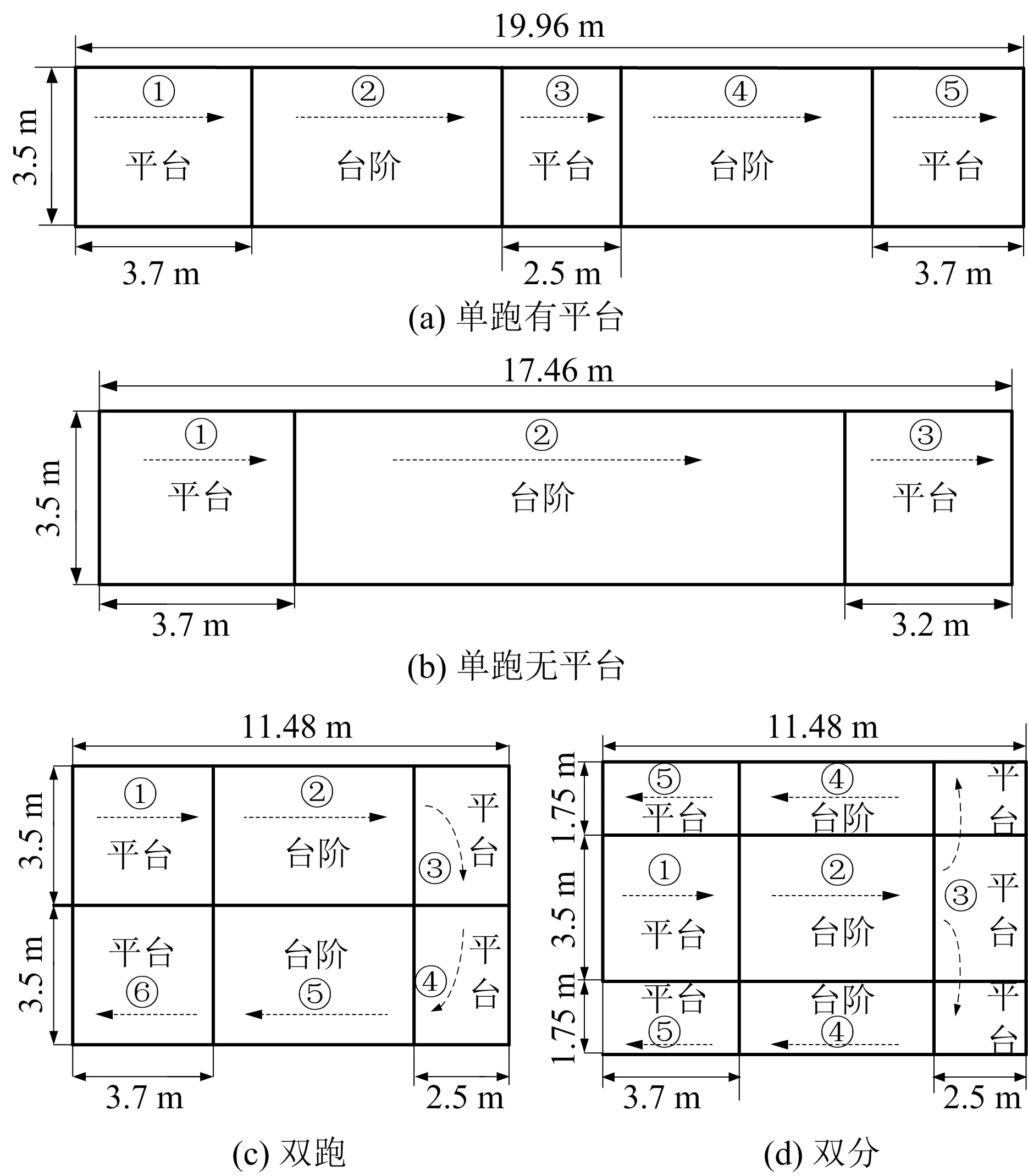
圖3 4種梯形平面示意Fig.3 Schematic diagram on the staircase configurations

2.3 仿真結(jié)果分析

用改進的三維社會力模型對4種樓梯類型進行模擬，得到其疏散場景圖及運動軌跡(圖4)。

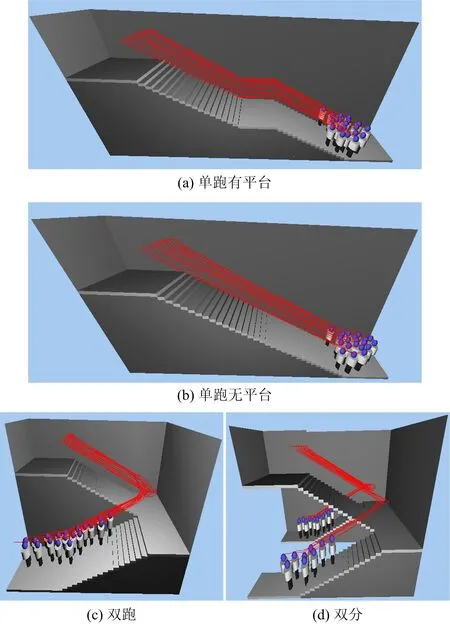
圖4 疏散場景圖及其運動軌跡Fig.4 Evacuation scene map and motion track

2.3.1 4種梯形總疏散時間

為了分析不同梯形中人員密度對疏散效率的影響，將初始人群密度劃分成低、中、高3個水平，即低于0.3人/m2為低密度人群，0.3～1.4人/m2為中密度人群，大于1.4人/m2為高密度人群[13]。根據(jù)樓梯面積，將初始人數(shù)分別設(shè)為10，20，60，80，120及130人，通過上述的三維社會力模型進行仿真，模擬結(jié)果如圖5所示。

圖5 不同人群密度下4種梯形的行人總疏散時間Fig.5 The total evacuation time of four kinds of stairs under different population density

從圖5中可看出，在限定空間中，隨著總疏散人數(shù)的增加，4種樓梯類型的疏散時間線性增加。在3種初始人群密度下，單跑無平臺梯形疏散時間最短，雙跑梯形疏散時間最長。如在初始人數(shù)為10人時，單跑無平臺疏散時間為22.645 s，單跑有平臺為26.590 s，雙分為27.808 s，雙跑為29.537 s；最大疏散時間差為7 s左右，最小疏散時間差為1 s左右。在初始人數(shù)為60人時，單跑無平臺疏散時間27.721 s，單跑有平臺為32.183 s，雙分為33.124 s，雙跑為37.094 s；最大疏散時間差為9 s左右，最小疏散時間為1 s左右。在初始人數(shù)為130人時，單跑無平臺疏散時間為32.303 s，單跑有平臺為36.788 s，雙分為38.410 s，雙跑為43.137 s；最大疏散時間差為11 s左右，最小疏散時間差為2 s左右。即單跑有、無平臺梯形布局在疏散時間上快于雙分、雙跑梯形布局；單跑無平臺梯形快于單跑有平臺梯形；雙分梯形快于雙跑梯形。這表明1個樓梯段疏散時間最短，而1個樓梯段中平臺的設(shè)置會延遲疏散；3個樓梯段的疏散時間比2個樓梯段短。

2.3.2 4種梯形平均疏散速度

為進一步分析不同梯形的疏散能力，用人員疏散速度指標(biāo)來反映疏散能力的快慢，即單位時間內(nèi)完成疏散的人員數(shù)量。先從宏觀角度來看4種布局樓梯在不同人群密度情形下的平均疏散速度，如圖6所示。

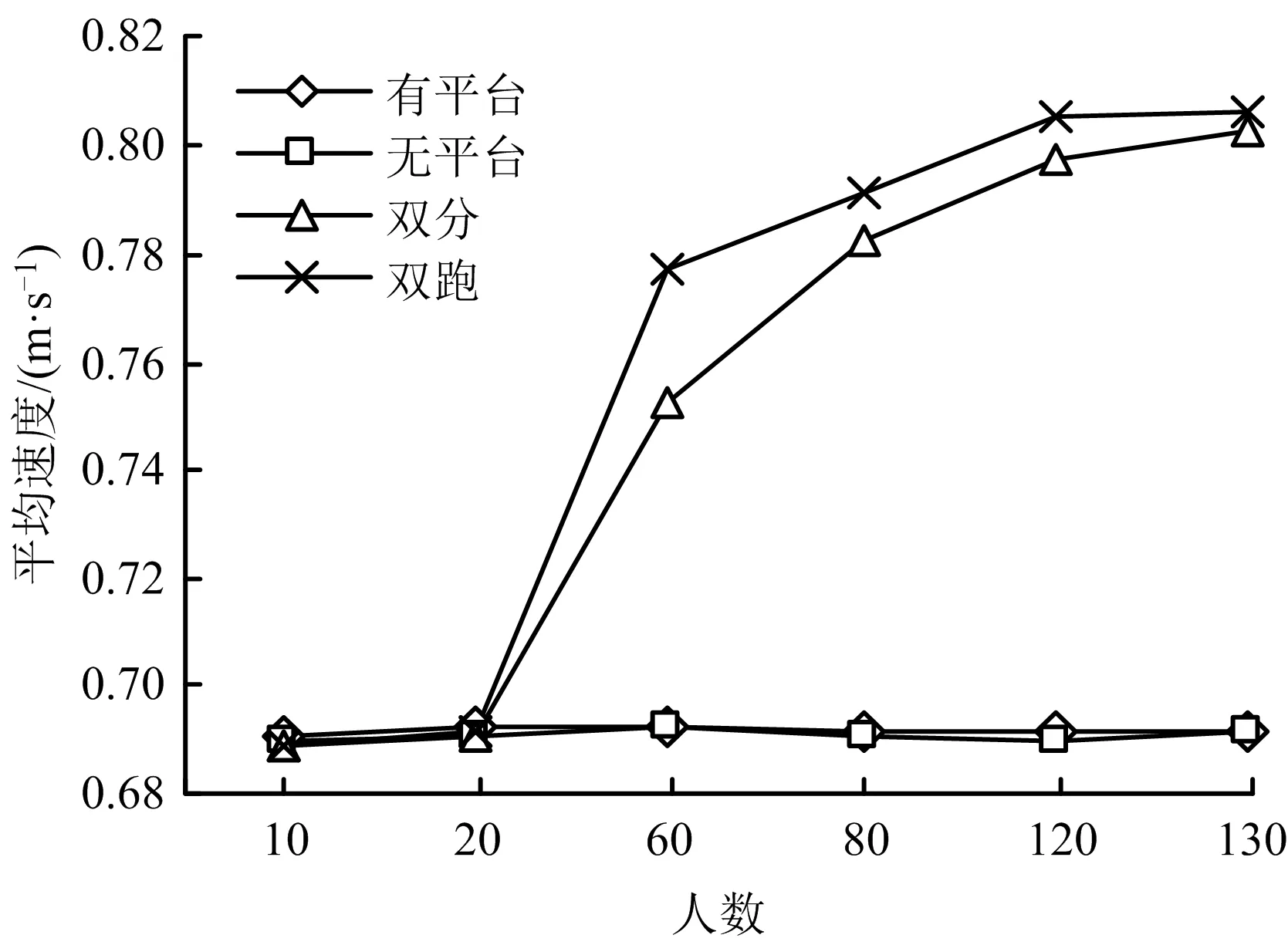
圖6 不同人群密度下4種梯形的行人平均疏散速度Fig.6 The average evacuation velocity of four kinds of stairs under different population density

首先，從圖6中可以看出，在初始人數(shù)為低密度情形下，在限定空間中4種樓梯布局的疏散速度接近，比如當(dāng)初始人數(shù)為20人時，單跑有平臺疏散速度為0.691 9 m/s，單跑無平臺為0.690 8 m/s，雙分為0.690 1 m/s，雙跑為0.691 8 m/s。速度都接近渴望速度0.7 m/s，這表明初始人數(shù)為低密度情形下，在限定空間內(nèi)考慮有無平臺梯形會有利于人員更快地疏散。

而在初始人數(shù)為中、高密度情形下，單跑有、無平臺的疏散時間短，但疏散速度小。從理論上講，在限定空間內(nèi)，由于結(jié)構(gòu)布局不同，人員在單跑有、無平臺樓梯上的疏散總路程比雙分、雙跑長，速度應(yīng)該也大于雙分、雙跑梯形。而從實際模擬結(jié)果上看二者的速度慢于雙分、雙跑，這表明相較于2個和3個樓梯段，1個樓梯段人員活動空間范圍小，會使人員相互碰撞而造成擁堵，最終導(dǎo)致人員在樓梯上的疏散速度變小。

比如當(dāng)初始人數(shù)為60人時，雙跑平均疏散速度為0.777 m/s，雙分為0.753 m/s，單跑無平臺為0.692 2 m/s,單跑有平臺為0.692 5 m/s。當(dāng)初始人數(shù)為120人時，雙跑平均疏散速度為0.806 m/s，雙分為0.797 9 m/s，單跑無平臺為0.690 m/s，單跑有平臺為0.691 m/s。值得注意的是，在中、高密度情形下，雙分、雙跑梯形平均疏散速度大于渴望速度0.7 m/s，說明此時人員之間并沒有發(fā)生擁堵，反而提高了人員疏散速度。但速度的增加并沒有帶來更短的疏散時間。這表明，雖然單跑有、無平臺疏散時間快于雙分、雙跑梯形，但其不具有分流特點，易發(fā)生擁堵，因此其事故風(fēng)險發(fā)生率也比雙分、雙跑梯形高。

其次，從圖6中可以看到，在3種密度情形下，單跑有、無平臺速度十分接近，但單跑無平臺疏散時間明顯快于單跑有平臺，最大時間差為5 s，最小時間差約為3.5 s。說明平臺的設(shè)置會延遲疏散時間，單跑無平臺比單跑有平臺更有利于人員的快速疏散。

最后，雖然在3種初始人群密度情形下，雙分疏散時間明顯快于雙跑。但在低密度情況下，雙分和雙跑梯形疏散速度相差不大。比如當(dāng)初始人數(shù)為20人時，雙分疏散速度為0.690 m/s，雙跑疏散速度為0.692 m/s；而中、高密度情況下，雙跑速度稍大于雙分速度。比如當(dāng)初始人數(shù)為60人時，雙跑疏散速度為0.777 m/s，雙分疏散速度為0.752 m/s。這是因為雙跑比雙分少1個樓梯段，人員擁擠在一起，但這種擁擠程度并不造成擁堵，反而提高了人員的速度。但其速度增加并沒有帶來比雙分更短的疏散時間。當(dāng)人群密度為高密度時，雙分、雙跑速度趨于接近。比如，當(dāng)初始人數(shù)為130人，雙分疏散速度為0.803 m/s，雙跑疏散速度為0.807 m/s。綜上可知，雙分梯形比雙跑梯形多了1個樓梯段，分流優(yōu)勢更能體現(xiàn)在疏散時間上。因此雙分比雙跑更有利于人員快速疏散，且發(fā)生事故風(fēng)險率也較低。

2.3.3 4種梯形密度和速度分布圖

為了探討這4種梯形的內(nèi)在物理機制，通過Voronoi方法得到其密度、速度分布圖。筆者選取初始密度為60，130人的密度和速度分布圖進行探討。圖7與圖 8分別表示單跑有平臺、單跑無平臺、雙跑、雙分4種梯形在中、高密度情形下的密度分布圖。圖9與圖10分別表示有平臺、無平臺、雙跑、雙分4種梯形在中、高密度情形下的速度分布圖。

圖7 60人的密度分布Fig.7 The density profiles for 60 people

圖8 130人的密度分布Fig.8 The density profiles for 130 people

圖9 60人的速度分布Fig.9 The velocity profiles for the stair for 60 people

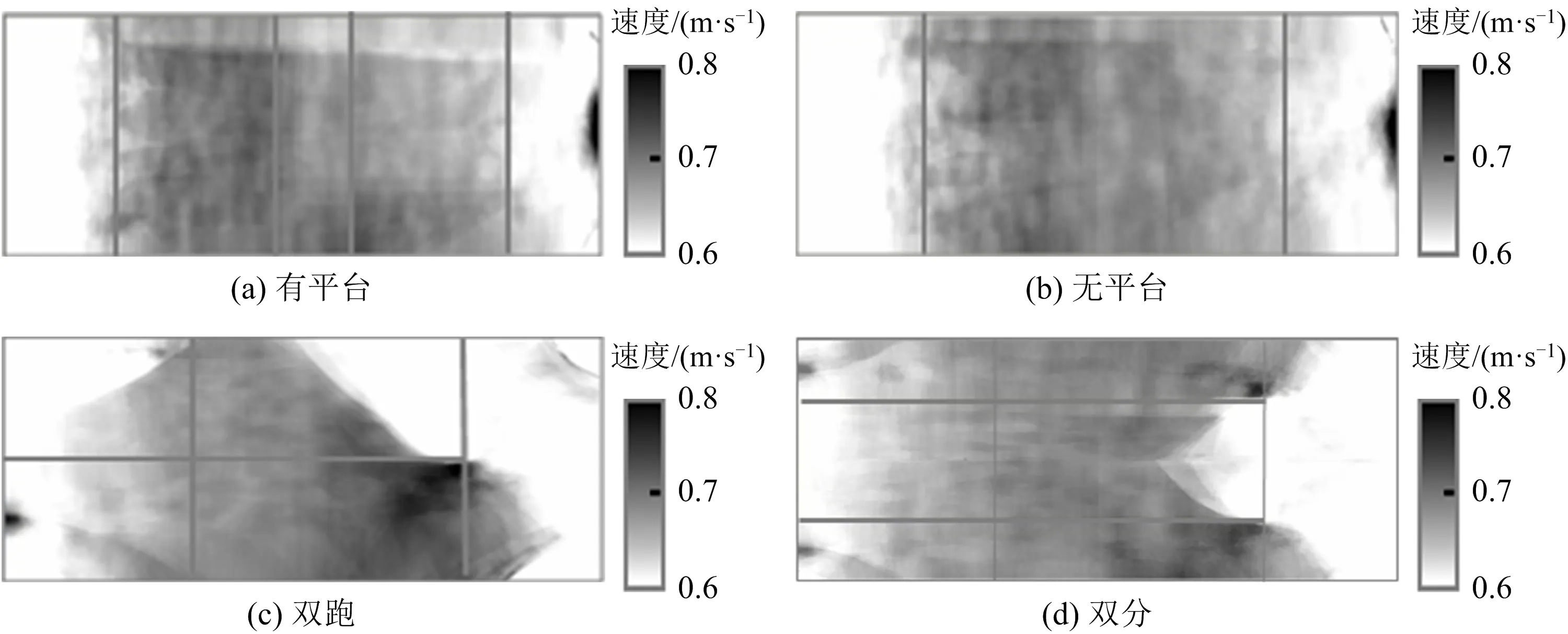
圖10 130人的速度分布Fig.10 The velocity profiles for 130 people

從圖7中可以看到，4種梯形在人員疏散過程中容易造成不同位置的聚集擁堵，即發(fā)生事故風(fēng)險的位置不同。如單跑有平臺和單跑無平臺2種梯形在樓梯開始疏散的上端和結(jié)束疏散的下端，其位置的密度值達到最大值(2.5人/m2以上)，而雙分梯形和雙跑梯形在上端樓梯和平臺連接處，即拐角處易造成人員擁堵，其密度值也達到2.5人/m2以上。值得注意的是，在相同人員密度情形下，雙分梯形由于分流特點，其易發(fā)生擁堵的部分比雙跑梯形小，這說明雙分梯形發(fā)生事故風(fēng)險的概率低于雙跑梯形。如在人員密度為130人時，可看到雙跑梯形易擁堵的位置面積約是雙分梯形的2倍。

根據(jù)泰森多邊形計算方法，單跑有平臺梯形在2種初始密度情形下，其最大密度值為5.51和6.45人/m2；單跑無平臺梯形的最大密度值為4.89和6.71人/m2；雙分梯形為3.06和5.35人/m2；雙跑梯形為4.55和6.13人/m2。

圖9、圖10表示4種梯形在2種密度情形下人員疏散的微觀速度分布狀態(tài)。從圖中可看到其速度值變化從中密度人群到高密度人群與圖6的趨勢相同。如圖9(a)中單跑有平臺梯形在初始人數(shù)為60人時，其最大速度值為0.81 m/s，平均疏散速度為0.692 5 m/s；圖10(a)中初始人數(shù)為130人時，其最大速度值為0.87 m/s，平均速度值0.691 8 m/s。圖9(b)、10(b)中的單跑無平臺梯形在2種密度下的樓梯區(qū)域最大速度分別為0.82和0.99 m/s，其平均疏散速度分別為0.692 2和0.691 9 m/s。即單跑有、無平臺速度分布相差不大。而雙分梯形和雙跑梯形的速度分布在2種密度情形下有明顯的顏色變化過程，即從中密度到高密度情形下，樓梯區(qū)域的灰色部分漸變到黑色部分。圖9(d)、10(d)中的雙分梯形樓梯區(qū)域最大速度分別為0.76和0.83 m/s，其平均疏散速度分別為0.752 7和0.802 8 m/s。圖9(c)、10(c)的雙跑梯形樓梯區(qū)域最大速度分別為0.82和0.83 m/s，其平均疏散速度分別為0.776 9和0.806 5 m/s。

3 結(jié)論

使用改進的三維社會力模型，仿真了4種樓梯布局的行人疏散過程，不僅從宏觀的總疏散時間和平均疏散速度指標(biāo)上對這4種梯形進行對比，還探討了其內(nèi)在物理機制，展示出區(qū)域的微觀速度和密度分布圖。研究發(fā)現(xiàn)：

1)在限定空間中，3種類型人群密度下，單跑無平臺梯形總疏散時間最短，雙跑梯形總疏散時間最長。

2)綜合考慮總疏散時間和平均疏散速度指標(biāo)，從安全和高效疏散角度上看，在限定空間中，單跑無平臺梯形有利于低密度情形下人員的快速疏散；而在中、高密度情形下，雙分梯形的分流特點更有利于人員的安全、快速疏散。

3)從微觀密度和速度分布圖可以清楚看到，4種梯形在人員疏散過程中均易造成人員聚集擁堵，但發(fā)生事故風(fēng)險的位置不同。單跑有、無平臺梯形在樓梯上端和樓梯下端易發(fā)生擁堵，此時速度值大，發(fā)生事故的風(fēng)險也大；雙分和雙跑梯形在樓梯與平臺的連接處易發(fā)生擁堵。

4)綜上，筆者建議在人員活動密集場所，如火車站、地鐵站等，選擇雙分梯形布局更有助于人群的安全、快速疏散。

在緊急疏散以及樓梯上有障礙物的情形下，4種樓梯布局的容納度以及疏散效果會有所不同，對此還要進行進一步的研究。