RFEHWSN中滿足節點吞吐量需求的負載均衡基站部署方案*
周衛元,陳立建,,徐欣晨,毛科技*
(1.浙江廣播電視大學蕭山學院,杭州 311200;2.浙江工業大學計算機科學與技術學院,杭州 310032)
無線傳感器網絡WSN(Wireless Sensor Networks)是由傳感器節點、匯聚節點(Sink node)和終端等3個部分組成的一種自組織網絡,由于應用場合的特殊性,傳感器節點一般由電池供電,電池更換比較困難或者花費代價比較高[1-2]。所以直接能從環境中捕獲能量的WSN被廣泛的進行了研究與應用,能從環境中捕獲的能量包括太陽能、熱能、射頻能量、振動能量、機械能等等[3-4]。射頻能量捕獲無線傳感器網絡RFEHWSN(Radio Frequency Energy Harvesting Wireless Sensor Network)可以通過不同物理環境和不同需要條件如時間、頻率、能量源的發送能量功率等維度上進行充分的控制,穩定性較強[5-6]。RFEHWSN 一般由能量源ET(Energy Transmitter)、基站BS(Base Station)和無線傳感器節點組成。
目前在RFEHWSN的研究進展有,文獻[7]給出了射頻能量捕獲無線傳感網中占空比最佳的能量源布置方法。文獻[8]描述了射頻能量捕獲異構無線傳感網的能量源最少化布置方法。文獻[9-11]對無線傳感網絡的射頻能量收集器,能量源移動路徑約束下時延最小化供電方案,射頻能量收集芯片等進行了研究。文獻[12]的模型也是點對點的平坦衰落信道下的無線系統,由于時變同信道信號干擾的存在,單天線接收方不僅要考慮如何收集發射機發射的干擾信號或者特定信號作為節點的能量供應,還要考慮如何解碼信息。文獻[13]提出了一種動態功率拆分的分配方案,即接收器接收到的信號一部分用以電池的供能,一部分用以信息解碼。在RFEHWSN的基站部署方面,文獻[14]研究了 RFEHWSN 中滿足節點吞吐量需求的基站最少化部署問題,提出一種低復雜度的啟發式部署算法和一種復雜度略高的基于遺傳算法的部署算法。文獻[15]以最少化基站和能量源數目為目標,研究了基站和能量源的聯合部署,滿足每個節點的平均能量捕獲功率比所需數據發送功率至少高出一個預定的閾值作為約束條件。本文考慮在異構射頻能量捕獲傳感網中,確定出滿足所有傳感器節點吞吐量所需求的最少基站個數,將其作為初始化部署,給定多于初始化部署所需個數的基站(如1.5倍的初始化基站個數),在不同基站數目下,部署基站滿足負載均衡,從而使節點的傳輸速率和網絡吞吐量滿足一個較優的水平。
1 系統模型
本節介紹滿足節點吞吐量需求的負載均衡基站部署的異構RFEHWSN模型。
1.1 網絡模型
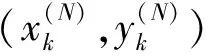
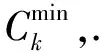
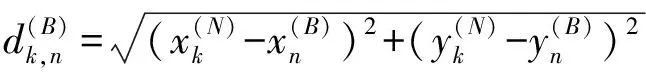
(1)
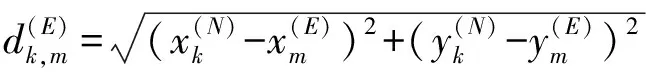
(2)
1.2 能量捕獲模型
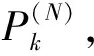
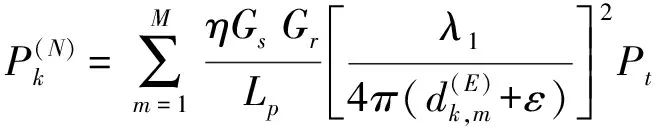
(3)
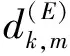
1.3 信息傳輸模型
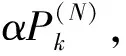
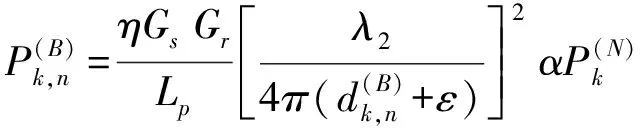
(4)
式中:λ2為數據傳輸信號波長。節點向基站傳輸信息,節點接入該基站。基站的接入量,也稱負載量,定義為接入該基站的節點數目(基站服務節點數)。根據信噪比公式,基站Bn從節點Sk處接收的信號的信噪比為
(5)
式中:no是高斯白噪聲的功率譜密度,W是信號帶寬。根據香農公式,可以得到節點Sk的實際吞吐量Ck為:
Ck=Wlog2(1+SNRk),k=1,2,…,K
(6)
綜上以上公式可得:
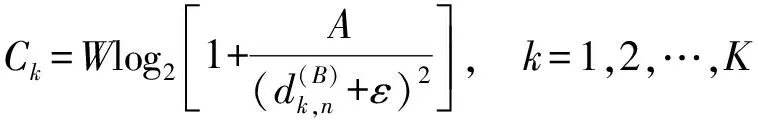
(7)
2 吞吐量較優的滿足負載均衡的基站部署方法
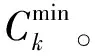
基于以上分析,最優基站部署問題可建模為優化如下問題:
目標:均衡各個基站的服務節點數量
變量:各個基站位置
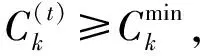
滿足全部節點的吞吐量需求的負載均衡基站部署方案為可行基站部署方案。在所有可行基站部署方案中,負載量最均衡的基站部署方案為最優基站部署方案。
由于基站數N是整數取值且節點的吞吐量表達式不是凸函數,該問題實際上是研究一個非線形和非凸優化問題,不能用凸優化理論解決。本文提出高效的啟發式基站部署方案,值得說明的是,該問題與ETs部署問題都屬于拓撲優化問題,但是由它們對應的數學優化問題可以知道,ETs部署問題中約束函數涉及的節點能量捕獲表達式與基站部署問題中約束函數涉及的節點吞吐量表達式有著顯著的不同。在ETs部署問題中,每個ETs位置的改變會影響所有節點所捕獲的功率,而在基站部署問題中,每個基站位置的改變只影響其周邊少數節點。因此,ETs部署問題的已有部署方案不適用于基站部署問題。此外,該問題與最小化基站問題也有著不同,最小化基站問題并不考慮每個基站的負載量,目的是基站數目最小。而在負載均衡基站部署中,需要優化的是每個基站的位置和接入量,基站數目的多少影響著整個網絡的基站負載量。
3 基站部署方法
本文定義以下幾個在基站部署方案中涉及的概念和定義。
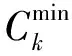
(8)
由式(7)、式(8)可知,距離基站越近的節點可以達到的吞吐量越高。
定理1在可行基站部署方案中,任意一個節點的需求圓內至少部署一個基站。
證明:通過反證法來證明。對于某個可行基站部署方案,假設一個節點的需求圓內沒有基站,那么該節點到最近基站的距離大于需求半徑,那么該節點達不到其吞吐量需求。因此,這與可行基站部署方案的定義相矛盾。證明結束。
定義2(最糟糕基站) 全網中服務節點數目最多的基站。
定理2存在一個最優部署方案,每個基站都是在最小覆蓋長方形內。
證明:通過反證法來證明。假設每個最優基站布置方案都有基站部署在最小覆蓋長方形外。任意挑一個最優基站布置方案,如圖1所示,有個基站部署在最小覆蓋長方形ABCD外的E點。現將該基站從E點沿著垂直于AD邊的線路上移動直至到達AD邊上的F點。易知,任一原先接入該基站的節點,到該基站的距離變得更短,因此該新基站部署方案仍為可行方案。證明成立。
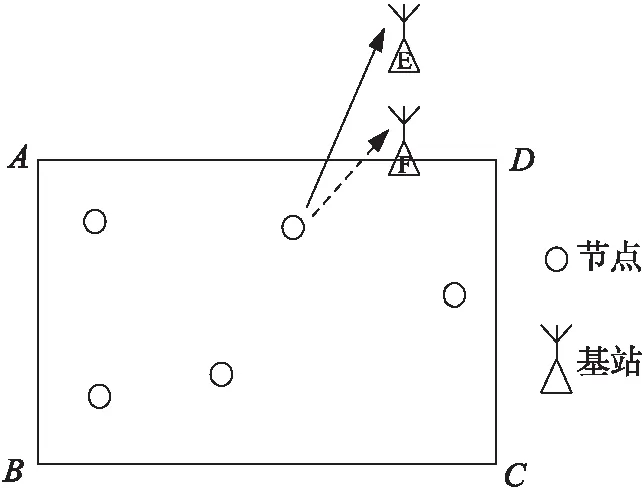
圖1 部署示意圖
在給定基站個數N和節點個數K時,平均基站服務節點數Bavg為
Bavg=K/N
(9)
每個基站的服務節點數越接近平均數,則部署方案越優。為了使本文的部署方案能更好地反映均衡性,本文采用基站負載量方差這個參數σ2來衡量。
定義基站負載量方差為
(10)
Bload是每個基站的負載量,方差越小,方案越優。
本文在初始化部署中,基站的部署方案要滿足約束條件,使每個節點滿足各自的吞吐量需求;在負載均衡部署中,始終滿足吞吐量約束條件基礎上對基站進行接入量的優化。
3.1 初始化部署
給定節點和ETs的位置和個數情況下,根據式(3)計算出節點的能量捕獲功率。給定各個節點的吞吐量要求下,再根據式(8)計算出各個節點的需求半徑和需求圓。
初始化部署方案滿足每個節點的吞吐量需求,所以我們可以執行某個已有的部署方案,將所需最小基站數目部署在網絡中,并將節點接入相應的基站。具體步驟如下:
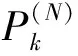
第2步 由節點的發送功率和最低吞吐量需求計算出各個節點的需求半徑rk. 和需求圓。
第3步 執行某個已有的部署方案(本文的方案)來將Nmin個基站部署到網絡中并將節點接入到這些基站。
第4步 確定剩余基站數N′=N-Nmin。
3.2 負載均衡優化部署
本文部署的主要目標是讓最糟糕基站達到負載均衡的效果,所以基站的接入量是唯一衡量指標,分別從兩個維度——節點和其余基站以均衡糟糕基站。對于節點而言,若其需求圓內基站個數大于1,節點進行信息傳輸基站的選擇就有很多種,為了滿足負載均衡,節點可以切換接入負載量較輕的基站進行信息傳輸。對于基站而言,若它原來所有的節點都已經切換到其余基站時,該基站可作為一個待移動基站,在性質上與未部署基站是一樣的(即此時接入量為0),該基站可以部署在最糟糕基站位置上,有效降低最糟糕基站的接入量。
因此,優化方案可分為4個部分:給定節點的切換優化、給定基站接入節點的切換優化、單個待移動基站的挑選和全網節點接入優化。
①給定節點的切換優化Node-Switch
當節點的需求圓內部署了不止一個基站時,為了滿足負載均衡,該節點就有選擇切換基站進行信息傳輸的權利。若節點當前傳輸信息的基站接入量相比較其他圓內基站更大,則該節點可以切換至接入量較小的基站上。在該模塊中,執行以下步驟:
第1步:對于給定的節點Sk,該節點的需求圓內的基站數目(記為I)大于1,即I>1,則節點進入準備切換狀態,當前接入的基站記為Bnow。
第2步:值得注意的是節點只會切換至負載量小于P的基站。在節點需求圓內找到負載量最低的基站B1。
第3步:判斷基站B1是否為Bnow。若不是,則節點切換至B1,否則繼續執行。
第4步:完成該模塊。
②給定基站接入節點的切換優化Nodes-Switch in BS
對于某個基站Bn下所有接入的節點,進行一個優化接入Node-Switch。具體步驟如下:
第1步 給定某個基站B,記此時基站負載量為P。
第2步 記錄接入該基站B的所有節點Sp(p=1,2…P)。
第3步 初始化p=1。
第4步 判斷p<=P是否成立,若成立,繼續向下執行,若不是,執行第8步。
第5步 對于節點Sp,判斷該節點的需求圓內是否有多個基站。
第6步 若該節點的需求圓內只有一個基站B,則該節點只能接入該基站B,執行第7步。否則,調用執行模塊Node-Switch。
第7步p=p+1,執行第4步。
第8步 完成該模塊。
③單個待移動基站的挑選Single Moving BS Selection
在這一模塊中,由于基站的負載量越低,其相應節點切換的復雜度越低,所以依次按照負載量從低到高的順序,嘗試從所有已經部署的基站中挑選出一個待移動的基站。當接入某個基站的節點可以全部切換到其他基站后,此時該基站的負載量為0,那么該基站就是待移動的基站,它可以去均衡負載量更重的基站。具體步驟如下。
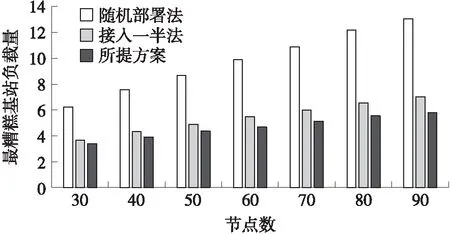
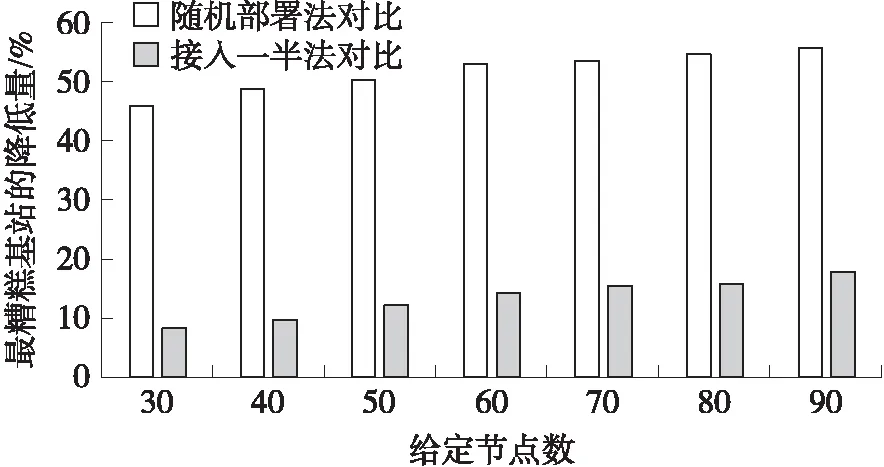
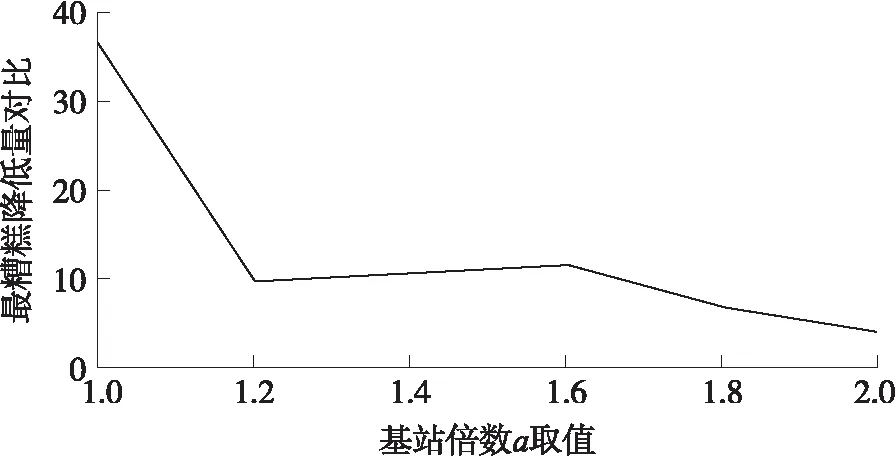
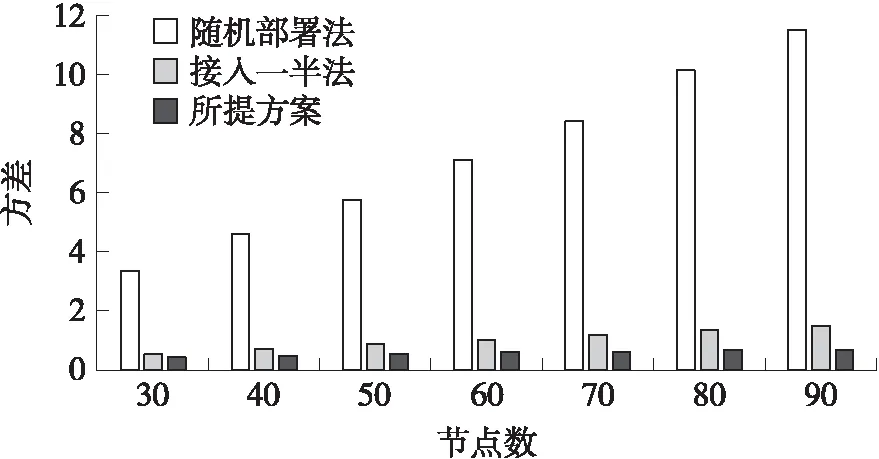
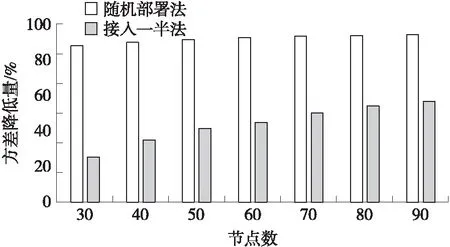
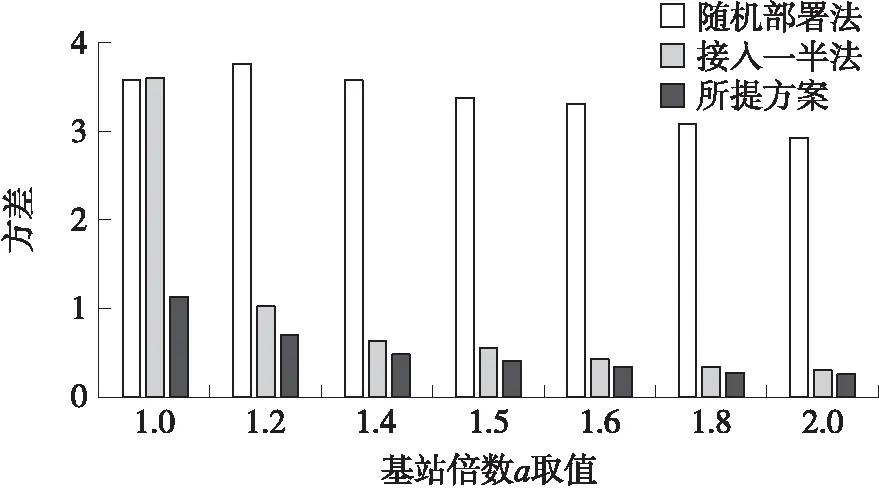
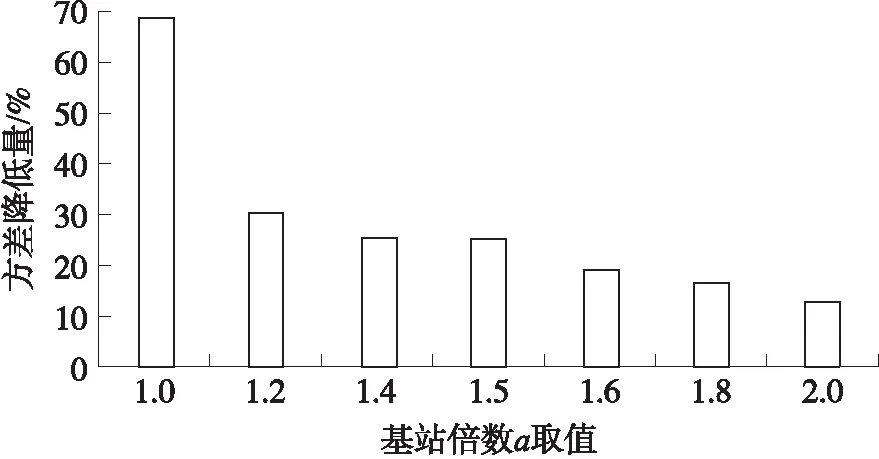
第1步:基站負載量進行從低到高排序,記為B1,Bi,…,BI,(1 第2步:判斷i 第3步:給定基站Bi,此時基站負載量記為P,記錄接入該基站Bi的所有節點Sp(p=1,2,…,P)。 第4步:判斷當前基站Bi下所有的節點Sp的需求圓內是否都存在至少兩個基站,只要存在一個節點的需求圓內只有一個基站,則Bi不能成為待移動基站,執行第7步。否則當所有的節點的需求圓內是否都存在至少兩個基站,繼續執行。 第5步:在所有的節點Sp的需求圓內將基站Bi標記可懸空。 第6步:節點Sp接入其需求圓內負載量最小的基站,執行第8步。 第7步:i=i+1,執行第2步。 第8步:退出。 ④全網節點接入優化All Nodes Optimization 在該模塊中,主要目標是均衡最糟糕基站的負載量,使得全網節點的信息傳輸相對較均衡。偽代碼如下: All Nodes Optimization 1. while(true) 2. 挑出當前最糟糕基站,執行將其一半的接入節點切換走; 3. if(Nodes-Switch in BS沒有進行任何節點接入的切換) 4. break; 5. end while 基于以上分析,優化部署的總體偽代碼如下: 負載均衡優化部署方案 Output:所需基站物理位置 Main procedures ①初始化部署 2. 將最小覆蓋長方形區域分割成p×q個小網格,并將這些網格標上序號,每個網格的中心記 為基站可能放置的位置。 3. 由節點的發送功率和最低吞吐量需求計算出各個節點的需求半徑rk。 4. 執行某個已有的基站部署方案(比如本文前面所提方案)來將Nmin個基站部署到網絡中,將 節點接入這些基站。 ②負載均衡優化部署 1. if(N>Nmin) 2. for(i=1;i<=N-Nmin;i++) 3. 從剩余基站中挑出一個,部署到最糟糕基站上; 4. 執行All Nodes Optimization進行全網節點優化; end for end if 5. while(true) 6. 執行Single Moving BS Selection嘗試挑出一個待移動的基站; 7. if(Single Moving BS Selection挑出了基站) 將其放在最糟糕基站邊上; 8. else return; 9. 執行All Nodes Optimization進行全網節點優化; end while 本文仿真實驗的場景是10 m×10 m的區域內隨機部署了K個傳感器節點,均勻部署了4個ETs,每個ET的發送功率Pt=0.1 W。能量捕獲模型和信息傳輸模型的相關參數如下[16]:η=0.3,Gs=8 dBi,Gr=2 dBi,Lp=3 dB,λ1=0.33 m,λ2=0.66 m,ε=0.2316 m,α=0.8。每種情況下的拓撲模擬1 000次。 采用的對比方案一,隨機對比法,即相同初始化部署后,如果還有基站未使用,則將剩余全部基站隨機放置在節點需求圓覆蓋范圍內,接著節點按照1/2的概率選擇是否進行基站切換;如果基站已經使用完,那么方案結束。 對比方案二,接入一半法,即相同初始化部署后,如果還有基站未使用,則每次將基站放置在全網最糟糕的基站旁,分擔其一半的接入量,直到所有基站全部部署;如果基站已經使用完,那么方案結束。 圖2 不同節點數下3種方案的平均最糟糕基站負載量(N=1.5Nmin) 圖2給出了當給定基站是滿足初始化部署所需基站(即滿足所有節點吞吐量需求的基站)的1.5倍,即N=1.5Nmin時候,3種方案在節點不同情況下,最糟糕基站的負載量對比。第2個圖是在第1個圖的基礎上,畫出的最糟糕基站降低量對比,更能直觀地看出所提算法的優勢。由圖中可以看出,所提方案在最糟糕基站負載量上均比兩個方案要優。 圖3直觀地反映了所提方案在最糟糕基站負載量上都比對比方案分別低,在隨機部署法對比中降低率在50%上下,在接入一半法對比中降低率在10%左右至20%左右,效果十分明顯。 圖3 不同節點數下3種方案的平均最糟糕基站負載降低量(N=1.5Nmin) 原因如下:隨機部署法存在十分大的偶然性,在初始化部署之后,剩余的基站隨機放置在節點需求圓覆蓋的區域內,不會非常準確地正好落在最糟糕的基站旁邊,所以該方案的最糟糕基站負載量較大。接入一半法與所提方案在初始化部署和全網節點接入優化All Nodes Optimization前半部分一樣,在滿足節點吞吐量需求后,將剩余基站輪次放置在最糟糕基站旁邊,分擔一半的接入節點。由圖可知,將剩余基站放置在最糟糕的基站旁邊,能有效地降低負載量。相比較隨機部署法,接入一半法和所提方案的最糟糕負載量明顯下降。而在本文所提方案有全網均衡的效果,不僅可以通過剩余基站降低負載,也可以通過已經部署好的基站來分擔最糟糕基站的負載量,所以所提方案還要比接入一半法在最糟糕基站負載量少。 圖4 不同基站數下接入一半法與所提方案最糟糕基站降低量對比,K=40 圖4給出了在節點數為40,給定不同基站下,即N=aNmin,a∈. {1,1.2,1.4,1.6,1.8,2}的情況下,所提方案與接入一半方案在最糟糕基站下的降低量對比。降低量先降低后上升再降低,但是始終所提方案的結果要更優。 在a={1,1.2}時,降低量降低,原因如下:在a=1時,接入一半法即為初始化部署,最糟糕的基站位置必然是全網節點需求圓重疊最高的區域,且重疊部分的節點都將接入該基站。而所提方案會在初始化部署基礎上進行優化接入,將最糟糕基站的負載量均衡到其他基站,所以在a=1降低量較高。當基站數目上升時,接入一半法存在剩余基站開始均衡最糟糕基站,與所提方案相差減少,所以降低量下降。 在a={1.2,1.4 1.6}時,降低量上升,原因如下:假設節點數40的情況下,最少需要4個基站,即Nmin=4,初始化部署基站分別接入21、8、8、3,最糟糕基站負載量為21。在接入一半法下,a=1.2,N=5,將剩余的一個基站放在最糟糕基站旁邊,均衡一半負載,此時所有5個基站部署結束,基站負載量為11、10、8、8、3,最糟糕基站負載量此時為11。當a=1.4,N=6,基站再增加一個,基站負載量分別為5、6、10、8、8、3,最糟糕基站負載量此時為10。當a=1.6,N=7,基站再增加一個,最后結果為5、6、5、5、8、8、3,最糟糕基站負載量此時為8。在所提方案中,初始化部署與接入一半法基站接入相同:21、8、8、3,最糟糕基站負載量為21。當a=1.2,N=5,將剩余的一個基站放在最糟糕基站旁邊,均衡一半負載,然后進行全網優化,基站負載量為10、10、8、8、4,最糟糕基站負載量此時為10。當a=1.4,N=6,基站再增加一個,優化后基站負載量分別為9、8、5、6、7、5,最糟糕基站負載量此時為9。當a=1.6,N=7,基站再增加一個,優化后放置最后結果為7、7、5、5、6、5、5,最糟糕基站負載量此時為7。為直觀起見如表1所示。 表1 負載量比較表 然而隨著基站數目的不斷增加,新增加的基站幾乎都覆蓋接入了所有接入量較大的基站,所以兩個方案中每個基站接入量介于平均,所以降低量減少。 如圖5,在a=1.5,N=1.5Nmin時,即給定的基站是滿足節點吞吐量需求下基站數目的1.5倍,可以從圖中清楚地看到,所提方案的方差σ2明顯優于兩個對比方案,方差越小,說明負載越均衡,且所提方案的方差均能保持在1以下,說明每個基站的負載量越均衡,也滿足了每個節點的吞吐量需求。 隨著節點數目的增加,本文的算法與隨機部署法方差降低量都維持在90%左右,如圖6所示。 圖5 不同節點數下3種方案的方差對比(N=1.5Nmin) 圖6 不同節點數下3種方案的方差降低量對比(N=1.5Nmin) 當節點數為30,即K=30,給定不同基站數目,即N=aNmin,a∈{1,1.2,1.4,1.6,1.8,2}下的3種方案方差對比。一方面,基站越多,所有方差都呈現下降趨勢;另一方面,本文所提方案均能保持一個較低的方差值,如圖7所示。 圖7 不同基站數下3種方案的方差對比(K=30) 圖8 不同基站數下所提方案與接入一半法的方差降低量對比(K=30) 圖8是圖7的更直觀表示,更有區分度地反映了所提方案與接入一半法在這種情況下方差的降低量,即使在給定最小基站數目兩倍的基站情況下,降低量依然能保持在10%以上。 本文提出了如何在獲得最小化基站個數并且滿足每個節點的吞吐量需求不少于一個門限值條件下,優化每個基站的負載量的方案,引入最糟糕基站的負載量和網絡基站負載量的方差作為優化指標。該方案分為兩部分:初始化部署和優化部署。初始化部署用最小的基站數目以滿足節點的吞吐量需求,優化部署的主要目的是達到負載均衡。其中,優化部署分為4個模塊,分別為:給定節點的切換優化、給定基站接入節點的切換優化、單個待移動基站的挑選和全網節點接入優化。節點可以通過切換需求圓內的基站以優化每個基站的接入量,負載量小的基站可以分擔負載量大的基站節點,同時網絡中也可以通過方差來判斷是否可以挑選出可以移動的基站來均衡全網最糟糕的基站。通過這些步驟優化部署,既要滿足每個節點吞吐量限制,也要讓每個基站負載量盡可能小。仿真結果表明,通過節點的優化接入能夠有效降低網絡基站負載量方差,達到負載均衡的效果。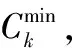
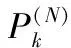
4 實驗仿真
4.1 最糟糕基站負載量比較

4.2 方差比較
5 總結

