考慮孔徑分布的低滲透煤層氣體滲透率計算模型

李立功，張曉雨，李 超，張潤旭，康天合

(太原理工大學 原位改性采礦省部共建教育部重點實驗室，山西 太原 030024)

滲透率在油氣田開發中起著十分重要的作用。井的數量、井間距的確定和儲層改造方式的選取等都離不開滲透率的準確獲取[1]。目前，獲得儲層滲透率的途徑主要有巖芯實驗室測量滲透率[2-3]、地震解釋滲透率[4]、電纜地層測試滲透率[5]、鉆桿地層測試滲透率[6]以及測井解釋滲透率等方法。但前幾種方法相對于測井解釋獲取滲透率，其成本較高，且受到各種限制。因此，在地層評價中常常利用測井數據來獲取連續的地層滲透率資料[7-8]。核磁共振測井技術[9-10]為基于測量信號直接反映儲層孔隙度分布的測量方法，不僅能夠測量孔隙度的大小，還能夠識別不同孔隙直徑所對應的孔隙度，最終得到不同孔隙類型及分布狀況，然后通過孔隙與滲透率的關系，建立測井滲透率模型，進而獲取儲層滲透率。采用測井方法可以較為全面的獲取儲層滲透率，但測井方法求取的滲透率的準確度主要依賴于建立孔隙結構與滲透率關系計算模型。因此，研究儲層孔隙結構與滲透率之間的關系，建立孔隙結構與滲透率關系模型是測井方法準確獲取滲透率的關鍵。目前常用的滲透率模型大都是基于平均孔隙半徑所建立的，如KLINKENBERG[11]、BESKOK和KARNIADAKIS[12]、COATES[13]、JAVADPOUR[14]、CIVAN[15]、ZIARANI[16]、李立功[17]等依據巖石的宏觀孔隙率或者將巖石孔隙等效為n個半徑相同的毛細管，并基于不同假設條件下的微管模型提出了氣體滲透率計算公式。CAO[18]、BANAVAR[19]、LATOUR[20]、BERNABY[21]、韓玉嬌[22]等在研究低滲透儲層滲透率時發現采用平均孔徑計算的滲透率與實測值有較大差異，對于常規儲層而言，其孔喉相對均勻，采用平均孔喉半徑來研究儲層滲透率準確度較好，但對于孔隙結構較為復雜的低滲透儲層而言，孔喉分布與常規儲層有明顯的區別，孔隙結構較常規儲層復雜的多，呈現強烈的非均質性特征，采用平均孔徑來計算儲層滲透率，忽略了儲層孔隙分布特征這一關鍵因素，其計算結果與儲層真實滲透率可能存在較大差距。

鑒于此，筆者針對我國山西地區低滲透煤層孔隙結構復雜的特點，提出利用核磁測井T2頻譜測得的孔隙分布資料，建立考慮孔徑分布特征的低滲透煤儲層氣體滲透率計算模型，使用實驗室試驗數據驗證模型計算結果的準確性;以孔徑分布符合高斯分布為例，分析孔隙分布特征對低滲透煤儲層滲透率的影響，比較新模型與基于平均孔徑計算滲透率的差異，分析新模型的適用性。

1 模型建立

1.1 基本假設

為了便于描述，對模型做如下假設:① 低滲透煤儲層孔隙可以等效為不同孔徑的微管，且各管之間不連通，微管長度為l=τL，其中τ為微管迂曲度;L為試件長度，如圖1所示;② 微管不可壓縮，即不考慮孔隙壓力變化引起的孔隙半徑變化;③ 不考慮氣體吸附、解吸引起的孔隙半徑變化。

圖1 低滲透煤儲層等效孔隙示意Fig.1 Equivalent pores of low permeability coal reservoir

1.2 考慮滑脫效應的單個微管流量計算

依據Klinkenberg給出在時間t內單個微管在半徑r0到r0+dr區域流過的氣體體積[11]為

(1)

式中，μ為氣體黏度，Pa·s;p為壓力，MPa;c為比例因子，一般取0.9，無量綱;λ為平均分子自由程，m。

通過整個微管橫截面積的體積為

(2)

根據氣體狀態方程，單位時間內微管中壓力p與氣體物質的量n的關系為

(3)

式中，R為普氏氣體常數，J/(mol·K);T為溫度，K;n為物質的量，mol。

將式(3)代入式(2)，整個毛細管長度上壓力與物質的量的關系為

(4)

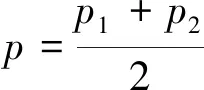
(5)

式中，p為毛細管內氣體平均壓力;p1為進口壓力，MPa;p2為出口壓力，MPa。

將式(5)代入式(4)得

(6)

理想氣體平均分子自由程λ的計算公式[23-24]為

(7)

將式(5)代入式(7)得

(8)

其中，M為氣體分子的質量,g/mol。將式(8)代入(6)得半徑為r0的單個微管在進口壓力p1出口壓力p2時的氣體流量Qg為

(9)

1.3 低滲透煤儲層氣體滲透率模型

將儲層孔隙等效為n1個孔徑為r1,n2個孔徑為r2，…，nn個孔徑為rn的幾何體，假設半徑為ri的孔，其分布頻率為f(ri)，則ni可表示為

(10)

其中，φ為儲層孔隙率。通過ni個半徑為ri孔的總流量Qg(ri)為

(11)

通過儲層的總流量Qg可表示為

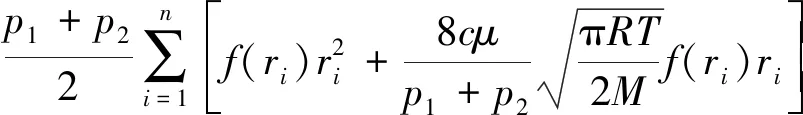
(12)

對于氣體在多孔介質中流動，其流量可表示為

(13)

由式(12)，(13)得考慮孔徑分布的氣體滲透率計算表達式為

(14)

2 模型驗證

采用山西西山煤田古交區塊8號低滲透煤樣孔徑分布及氣體滲透率測試數據進行實例驗證。核磁共振測井作為目前惟一能夠表征儲層孔隙結構的測井方法，具有快速、無損害、可重復等優點，能夠實現致密巖石微米-納米級孔隙的高精度測量[25-26]。因此，本試驗孔徑分布測試采用核磁共振T2譜獲取。試驗使用儀器為上海紐邁公司生產的MesoMR23-060H-I型核磁共振儀，共振頻率為21.68 MHz，射頻脈沖頻率21.68 MHz。將現場取回煤樣制成φ25 mm ×60 mm 的規格制成圓柱形煤樣，將煤樣放在干燥箱中干燥12 h以上，將干燥過后的煤樣放入核磁共振儀中采集樣品的T2頻譜，將采集的T2頻譜通過式(15)獲取孔徑分布[27-28]:

(15)

式中，Fs稱為幾何形狀因子，對球狀孔隙，Fs=3;對柱狀管道，Fs=2;ρ2為巖石的橫向表面弛豫強度，μm/ms。

不同煤樣核磁共振孔徑分布如圖2所示。

基于平均孔徑計算氣體滲透率計算采用Klinkenberg給出的氣體滲透率式(KLINKENBERG L J，1941):

(16)

(17)

考慮孔徑分布氣體滲透率計算依據式(14)。

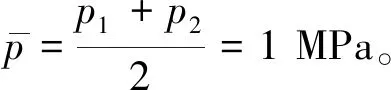
圖3 試驗數據、模型計算數據及平均半徑計算滲透率比較Fig.3 Comparison of test data,model calculation data and average radius calculation permeability

圖4 滑脫系數隨孔徑變化關系示意Fig.4 Schematic diagram of the relationship between slip factor and pore diameter

3 孔徑分布特征對氣體滲透率的影響——以孔徑分布符合高斯分布為例

為了方便計算，假設孔徑與孔徑分布頻率滿足高斯函數，則低滲透煤儲層孔徑分布頻率可表示為

(18)

3.1 孔徑分布標準差σ對氣測滲透率的影響

3.1.1影響規律

假設孔隙率φ=12%不變，期望ν=0.5，標準差σ=0.05,0.07,0.10,0.13和0.18時，孔徑分布如圖5所示。

圖5 期望為0.5時不同標準差下的孔徑分布Fig.5 Pore diameter distribution diagram for different standard deviations under the expectation is 0.5

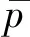
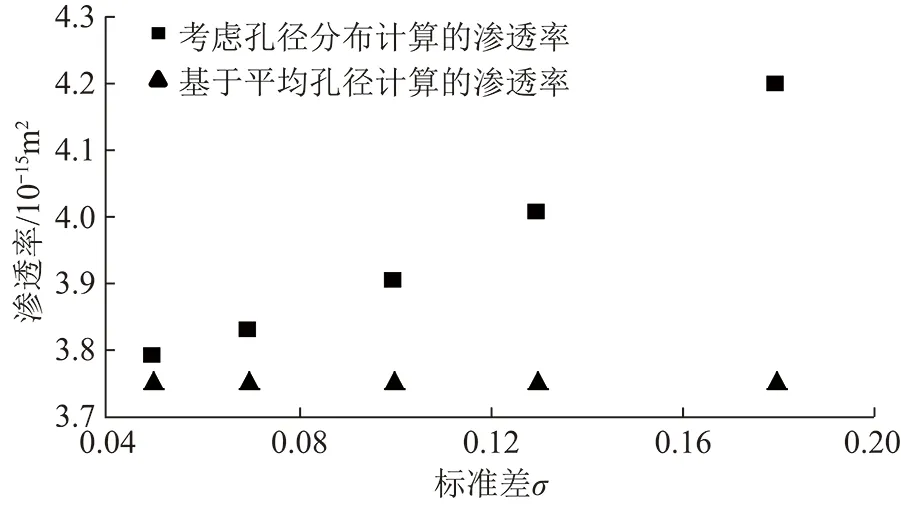
圖6 考慮孔徑分布與基于平均孔徑計算滲透率隨標準差變化Fig.6 Considering the pore size distribution and the variation of calculated permeability with standard deviation based on average pore size

圖7為不同標準差下新模型計算結果與基于平均孔徑計算結果差異隨標準差變化關系。可以看出隨標準差的增加考慮孔徑分布與基于平均孔徑氣體滲透率計算模型計算的氣體滲透率差異逐漸增大，即在孔隙分布符合高斯分布時，低滲透煤樣的孔隙越集中兩者差異越小，孔隙分布越分散其差異越大。兩者差異由σ=0.05時的0.97%增加到σ=0.18時的11.78%。從考慮孔徑分布模型與基于平均孔徑模型計算氣體滲透率結果的差異可以看出，在研究孔隙較為均勻的常規儲層時，即標準差σ較小時，基于平均孔徑方法計算的滲透率往往誤差較小，采用平均孔徑計算氣體滲透率基本能滿足預測需要，但對于孔隙分布較為復雜的低滲透煤儲層而言，即σ較大時，孔隙越復雜(σ越大)其計算結果準確度越差，此時孔徑分布特征對滲透率的影響不容忽視，在計算低滲透煤儲層氣體滲透率時基于平均孔徑計算氣體滲透率已不能準確獲取滲透率值，必須考慮孔隙分布特征對滲透率的影響。

圖7 考慮孔徑分布模型計算與基于平均孔徑模型計算的氣體滲透率差異率隨標準差變化關系Fig.7 Relationship between the gas permeability calculated by the new model and the difference of gas permeability calculated based on average pore diameter varies with standard deviation

3.1.2影響機理分析

對于半徑為r、長度為l的單個微管而言，其在進口壓力為p1，出口壓力p2(p1>p2)時通過單管的流量Qg(r)可將式(9)表示為

(19)

對Q(r)求二階導為

(20)

由于p1>p2，r>0，所以Q″(r)>0，根據二階倒數的性質可知

Qg(r+dr)+Qg(r-dr)<2Qg(r)

(21)

因此，在計算氣體滲透率時考慮孔徑分布計算的滲透率略大于基于平均孔徑所計算的滲透率。在孔隙率和平均孔徑相同時，σ越大，偏離平均孔徑孔隙所占的比例越大，考慮孔隙分布和基于平均孔徑所計算的滲透率差異越大，基于平均孔徑所計算的滲透率誤差越大。

3.2 孔徑分布期望ν對氣體滲透率的影響

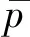
圖8 不同期望ν下的孔徑高斯分布Fig.8 Pore diameter of gaussian distribution under the different expectations ν

圖9 氣體滲透率隨期望變化關系Fig.9 Relationship between gas permeability and expectations

圖10 考慮孔徑分布與基于平均孔徑計算氣體滲透率差異率隨期望變化Fig.10 Difference between the new model and the calculated gas permeability based on average pore diameter varies with expectation

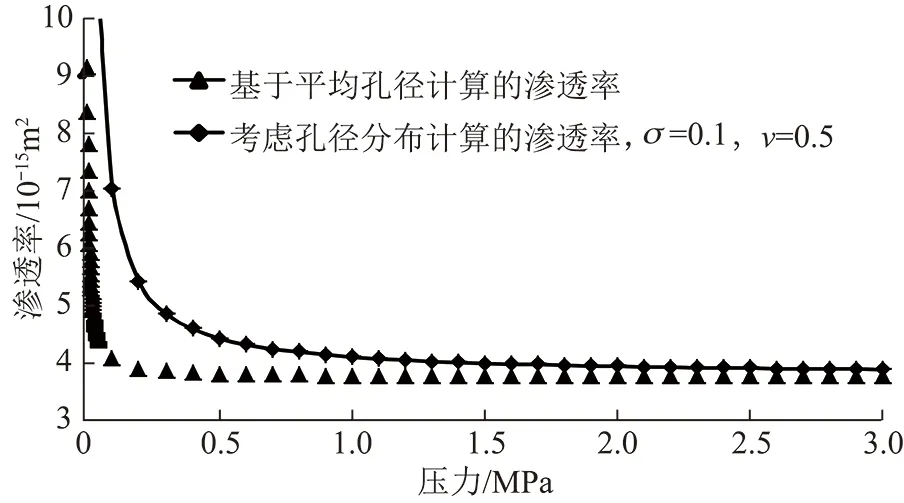
圖11 考慮孔徑分布與基于平均孔徑計算氣體滲透率隨壓力變化Fig.11 Change of gas permeability with pressure based on average pore diameter under the considers of the pore diameter distribution

3.3 氣體壓力對氣體滲透率的影響

圖11為孔徑分布為標準差σ=0.1，ν=0.5時考慮孔徑分布與基于平均孔徑時氣體滲透率計算結果。由圖11 可以看出，隨著壓力的降低，氣體滲透率急劇增加，壓力越低滲透率增加幅度越大，這是由于氣體滑脫效應的存在，壓力越低，氣體滑脫效應越明顯，滲透率增加越快。兩種方式計算的滲透率在壓力大于1 MPa時，兩者差異不明顯，并且滲透率隨壓力減小變化均不大。考慮孔徑分布計算的滲透率在壓力小于1 MPa后，滲透率變化模型，呈快速增加趨勢;基于平均孔徑計算的滲透率在壓力小于0.2 MPa后才呈現快速增加趨勢。這是由于孔徑越小，滑脫效應引起的滲透率變化量對壓力的變化越敏感，考慮孔徑分布滲透率計算模型考慮了小于平均孔徑滑脫效應對滲透率的影響。

圖12為考慮孔徑分布與基于平均孔徑計算滲透率隨壓力變化的差異。由圖12可以看出，隨著壓力的降低，兩者差異越來越明顯，呈增大趨勢。這是由于小于平均孔徑孔在低壓時，滑脫效應的增量隨孔徑變化的非線性關系，使得考慮孔隙分布計算的滲透率與基于平均孔徑計算的滲透率差異逐漸增大。

圖12 考慮孔徑分布與基于平均孔徑計算滲透率差異隨壓力變化Fig.12 Calculated permeability difference with pressure based on average pore diameter under the considers of the pore diameter distribution

4 結 論

(1)對于低滲透煤儲層而言，考慮孔徑分布特征的氣體滲透率計算結果較基于平均孔徑的氣體滲透率計算結果與實測數據吻合度更好，計算結果更為精確。

(2)對于孔徑較小、孔隙分布復雜的低滲透煤儲層而言，采用理論計算的方法計算氣體滲透率時孔徑分布特征對氣體滲透率的影響不可忽略。

(3)在孔隙率和期望ν一定時，σ越大，低滲透煤儲層的氣測滲透率越大，與基于平均孔徑計算的氣體滲透率差異越大，當σ=0.18時兩者計算結果差異可達11.78%;在孔隙率和標準差σ一定時，ν值越大，氣體滲透率越大，與基于平均孔徑計算的氣體滲透率差異越小;在孔隙率相同時，壓力越低考慮孔徑分布與基于平均孔徑計算的氣體滲透率差異越大。針對孔隙分布復雜的低滲透煤儲層，計算氣體滲透率時，新模型較基于平均孔徑模型更為準確。