基于滑動窗迭代最大后驗估計的多源組合導航因子圖融合算法

徐昊瑋， 廉保旺， 劉尚波,2

(1.西北工業大學 電子信息學院, 陜西 西安 710072； 2.中國科學院 西安光學精密機械研究所, 陜西 西安 710119)

0 引言

通過內部子導航系統間共享信息和性能互補，配備不同類型導航源的多源組合導航系統，能夠在復雜環境中為各種平臺提供連續且準確的導航解決方案。信息融合是多源組合導航系統中的最基本問題，近年來已有許多研究集中于各種導航源的相互融合，如全球衛星導航系統(GNSS)、慣性導航系統(INS)、激光測距(LiDAR)系統、磁力計、計算機視覺或超寬帶(UWB)定位系統等[1-3]。在許多基于INS的多源組合導航系統中[4-6]，集中式卡爾曼濾波算法經常被用來處理所有觀測量，并提供全局最優估計。盡管集中式卡爾曼濾波可以避免觀測信息的丟失，但隨著導航源數量的增多，急劇增加的計算負擔和較差的系統容錯性會使得整個融合系統的性能下降。

針對上述問題，聯邦卡爾曼濾波器[7-8]作為一種分散化的卡爾曼濾波算法，逐漸受到關注。聯邦卡爾曼濾波器由眾多子濾波器和一個主濾波器組成，它是一種具有兩階段數據處理的算法。在進行多源組合導航數據融合的過程中，子濾波器將子導航源輸出的導航觀測量與參考導航源輸出的導航解進行融合，從而得到局部導航狀態估計值，而局部導航狀態估計值和子系統協方差矩陣被輸入到主濾波器中，計算全局最優估計并更新全局協方差矩陣。然而，由于不同子導航源之間異步的數據更新以及在線和離線傳感器之間的切換，在主濾波器融合過程中各個局部導航觀測量的時刻并不統一，導致引入全局估計誤差。一些研究通過引入內插或遞推的算法，將子系統的時刻統一，但也因此會引入人為誤差，增加了計算負擔[9]。

為了解決多源組合導航融合應用中存在的上述問題，文獻[10-12]提出了一種基于因子圖的多源組合導航信息融合算法。因子圖算法(簡稱FG算法)是一種基于圖的貝葉斯推理平滑算法[13]，它為即插即用型傳感器提供了靈活的應用基礎。在FG算法中，傳感器網絡中的每個觀測量被編碼成一個因子，所有傳感器的觀測因子通過節點互連的方式組成框架圖，通過對這些連接在框架上的因子使用貝葉斯推理完成數據融合和參數估計。由于在多源組合導航系統中，各導航源更新觀測量的速率不一致，因此采用更新速率最高的INS作為主導航源，當在某時刻從任意子導航源獲取測量結果時，首先利用INS中的慣性測量單元(IMU)輸出數據進行預積分和定位解算，來計算未知觀測節點的預測值；然后將觀測量作為后驗信息，通過迭代得到各節點狀態量的全局最大后驗估計。文獻[14]在此基礎上進一步將滑動窗的概念引入多源組合導航因子圖算法中。滑動窗使得因子圖的全局最優化過程僅發生在最新生成的若干個節點間，它的引入不僅提高了融合算法的估計速度，而且減少了算法的計算量。

多源組合導航因子圖融合算法的最優化過程是通過最小化觀測量與預測量之間的馬氏距離[15]實現的，馬氏距離與子系統先驗誤差分布的均值向量和協方差矩陣相關，在上述FG算法[10-14]中，觀測量的誤差分布一旦完成初始化后將保持不變。然而，由于各種環境因素的影響，非慣性導航源的觀測量是時變的，當融合算法中觀測量誤差的先驗估計與實際得到的觀測量存在差異時，就會導致估計結果相對于真實值存在較大偏差，因此需要引入算法對觀測量誤差進行實時的估計。基于以上原因，本文提出了一種基于高斯模型下的子系統觀測量均值向量和協方差矩陣的估計算法，該算法能夠通過迭代選權的方式對觀測量誤差分布狀態進行準確、快速地估計，進而提高FG算法對導航狀態估計的精度。

1 基于滑動窗的因子圖組合導航系統模型

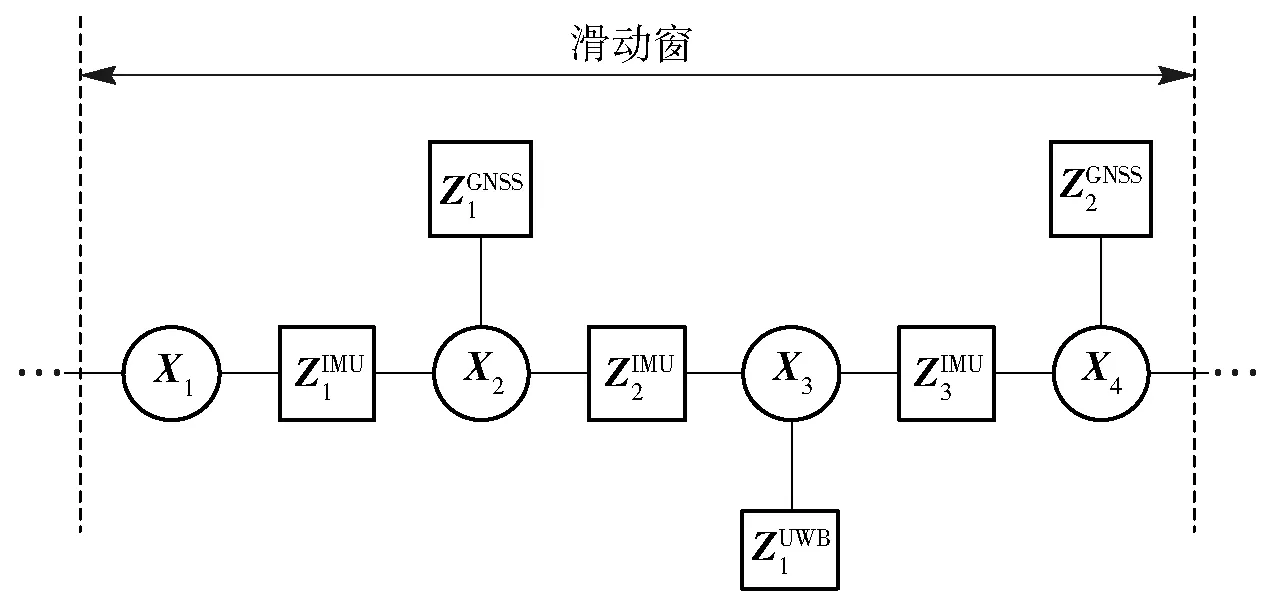
圖1 多源組合導航FG算法的原理示意圖Fig.1 Schematic diagram of factor graph-based multi-source integrated navigation data fusion algorithm

在FG算法中，應用貝葉斯推斷進行狀態量估計的范圍可以是整個因子圖網絡，但是遍歷估計的方法使得算法在運行過程中的計算量不斷增大，而且最新得到的觀測值對早期變量估計準確性的提高也并不顯著。因此通過對因子圖的優化范圍加窗，即限定參與優化的因子節點范圍，能夠有效減少算法計算量、提高算法的效率。

滑動窗因子圖意味著滑動窗口內僅包含全部因子節點中的一部分，它類似于固定滯后平滑算法。然而，與傳統的線性平滑器不同，滑動窗因子圖可以通過應用增量平滑算法，在每次產生新觀測量時無需重新計算整個雅克比矩陣，僅需要對經過正交三角分解(QR)的雅克比矩陣進行增量更新即可。滑動窗FG算法中加窗的范圍即是應用貝葉斯推斷進行狀態量估計的范圍，滑動窗的滑動規則包括定步長、變步長和定窗長、變窗長[15]。滑動規則的選擇一般與應用場景相關，如在動態性變化較大的應用場景中，一般采用定步長、變窗長的滑動規則，從而保證算法能夠根據載體動態性自適應地調整估計值輸出速率。而在本文的應用場景下，由于信號和載體運動狀態的動態性變化相對較小，選取定步長、定窗長的滑動規則。本文中加窗的范圍是通過設定觀測量數目而確定的，即當觀測節點達到設定上限時，則產生新的窗。

2 因子圖組合導航融合算法

2.1 FG算法

為了實現導航系統中的數據融合，首先建立k時刻導航坐標系下的狀態變量Xk為

(1)

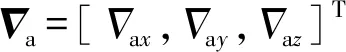
需要說明的是，之所以選用導航參數而非導航參數誤差作為系統的狀態量，主要是基于兩方面的考慮：1)將導航參數作為系統狀態變量，可以通過系統模型直接描述系統導航參數的動態過程，相比于根據1階近似推導得到的基于導航參數誤差狀態量，導航參數能夠更加準確地反映真實狀態的演變[16]；2)對更新的IMU數據進行預積分和解算后，無需等待子系統觀測量更新，可以直接建立因子節點并加入因子圖中[7,18]。導航參數的微分方程為

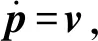
(2)

(3)

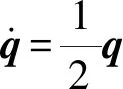
(4)

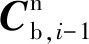
pi=pi-1+vi-1Δt，

(5)

(6)

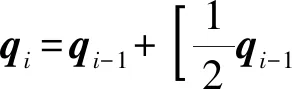
(7)

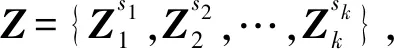
(8)

該后驗概率密度函數似然概率密度f(Zi|Xi)和先驗概率f(Xi|Xi-1)呈比例，即

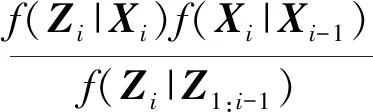
(9)

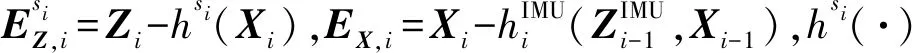
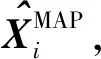
(10)

(11)

(12)

(13)

上述因子圖編碼的優化問題一般由高斯-牛頓迭代算法求解，(14)式所示為高斯-牛頓迭代算法的迭代規則[10]：

(14)

式中：ΔX=[ΔX1，ΔX2，…，ΔXk]；J()為包含滑動窗內所有節點的全局雅克比矩陣，

J(

(15)

r()=[r1,r1,…,rk]為當前估計值下的觀測量殘差，

(16)

在高斯-牛頓迭代求解過程中，需要在每個迭代周期內應用最小二乘法計算ΔX的值，一旦計算得到ΔX，則將+ΔX的值作為下次迭代的初始值，若ΔX足夠小或者超出迭代次數則取當前值作為最終的狀態估計量。(15)式中JZ和JX的導數可以分別通過(17)式～(19)式計算得到：

(17)

(18)

(19)

2.2 增量平滑算法

隨著系統工作時間的逐漸增加，FG算法中產生的因子節點逐漸增多，而每次因子節點的產生都需要重新求解已有各個因子節點中狀態量的最優估計值，但每次最優化過程都需要重新產生J矩陣，并對J矩陣進行QR分解，得到平方根信息矩陣R，以完成矩陣求逆和最小二乘解的計算，上述過程會帶來較大的計算負擔，也對系統的實時性造成了影響。

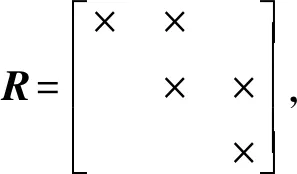
假設(20)式所示為通過QR算法計算得到的當前因子圖的平方根信息矩陣R[10]：

(20)

式中：×表示矩陣中的非0元素。

當有新的因子節點產生時，對應的平方根信息矩陣R′為

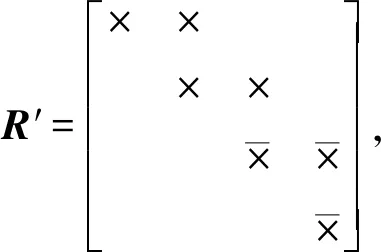
(21)

2.3 時變導航子系統觀測量狀態對FG算法的影響

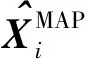
最大似然估計法是傳統的μ和Σ的估計算法[18]，假設p為Xi的維數，m為樣本數量，最大似然估計算法只有滿足m?p，才能得到較為準確的估計值。然而在多源組合導航的應用中，各導航源的觀測量更新速率不同，且測量精度變化較快，如果應用最大似然類估計算法則會造成估計滯后或估計誤差大的問題。最大后驗估計在最大似然估計的基礎上又增加了先驗概率的輔助，而先驗概率的加入使得估計在較小的數據集中能夠保持有良好的泛化性能[19]。基于以上原因，本文在傳統最大后驗估計算法的基礎上提出了一種應用于因子圖的迭代型均值向量和協方差矩陣的最大后驗估計算法。

3 均值向量和協方差矩陣的最大后驗估計

3.1 導航狀態分布參量的迭代最大后驗估計

最大后驗估計融入了待估計量的先驗分布，因此最大后驗估計可以看作規則化的最大似然估計。以觀測誤差EZ為例，為了在樣本數量遠低于估計量維度數量的情況下得到較為準確的μZ和ΣZ估計值，首先假設μZ和ΣZ服從Gaussian-Wishart分布，即(μZ,ΣZ)～NIW(μZ0,k0,v0,Ψ)，其中μZ0為μZ的均值，Ψ為ΣZ的先驗值，v0為ΣZ的自由度，k0為μZ協方差的尺度因子，μZ與ΣZ的聯合概率密度[20]可以表示為

(22)

式中：

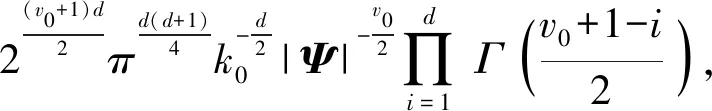
(23)

d為數據的維度數；μ0為所有導航源的均值向量。

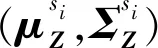
(24)

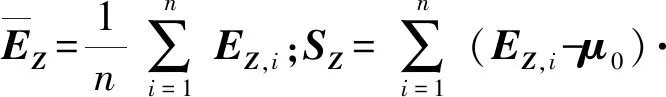
(25)

(26)

(27)

(28)

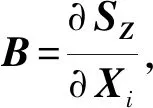
(29)

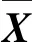
(30)

(31)

另外，在傳統基于滑動窗的FG算法中，由于在優化過程中對狀態量和觀測量的分布不進行更新，當優化窗向前滑動時，無需進行特殊的操作，直接應用先驗分布進行優化操作。但是在本文提出的基于迭代最大后驗估計的因子圖IMAPFG算法中，當窗向前滑動時，需要將上一時刻估計得到的狀態量和觀測量分布作為新窗中各個狀態的先驗分布，即μZ0和Ψ.

最后需要說明的是，對協方差矩陣的動態估計，實際上是一種動態加權的過程，即當某一時刻測量值的殘差較大時，估計得到的協方差矩陣也會相應增大，因此在下一次迭代周期中起到了降低權值的作用。隨著迭代的不斷進行，對于該觀測值的信任會不斷下降，該過程有助于提高融合算法對于野值點干擾的魯棒性。而算法中對于均值向量的估計一方面能夠提高協方差矩陣估計的準確性，另一方面，則能很好地解決由觀測量偏置而引起的融合算法異常的問題。

綜上所述，本文所提出的IMAPFG算法步驟為：

1) 設置各導航系統與因子圖初始參數，并定義狀態空間向量，確定滑動窗范圍。

2) 當子導航系統輸出測量值時，首先產生新的狀態節點加入因子圖中，并應用(5)式～(7)式根據IMU系統的觀測量計算該狀態節點的初始值，同時將產生觀測節點連接到該狀態節點上。

3) 判斷是否滿足滑動窗口范圍：當超出窗口范圍時，向前滑動窗或產生新的窗，并將上一窗內估計得到的狀態量和觀測量分布作為當前窗的先驗估計；當滿足滑動窗口大小時，則直接進行步驟4.

4)應用(14)式對窗口范圍內的因子圖進行最優化融合，并根據(27)式～(31)式對各系統的協方差矩陣和均值向量進行更新，當達到迭代次數上限或者殘差足夠小時退出迭代。

5) 輸出滑動窗內各狀態節點的狀態估計值，將各系統的協方差矩陣和均值向量的最終估計值作為下一個滑動窗內各參量的初始值，滑動窗向后移動l個節點，返回步驟2.

3.2 迭代更新對最優化系統收斂性的影響

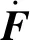
在FG算法中，非線性算子F為多個因子節點根據(5)式～(7)式進行狀態更新的集合，對F關于各個因子節點狀態求導，即可得到J矩陣，因此F可導。在3.1節中提出的最優化算法中，J矩陣在每個迭代周期內都根據觀測值進行調整，分析(15)式與(17)式～(19)式可知，新算法對J矩陣的調節相當于對矩陣中的各行元素分別乘以一個常數，如(32)式所示：

(32)

式中：Ji為矩陣J的第i行；ai表示新算法對矩陣J中第i行的調節系數。根據矩陣行列式的性質可知J′的行列式滿足：

(33)

4 測試實驗設置

為了驗證本文提出的IMAPFG算法的性能，分別進行了仿真測試與實驗測試。在仿真測試中產生了不同種類的傳感器測量變化，并將融合結果與真實參考值比較，可以定量地評價各種算法的優劣；而在實驗測試中，則應用了真實的傳感器數據驗證融合算法的性能。

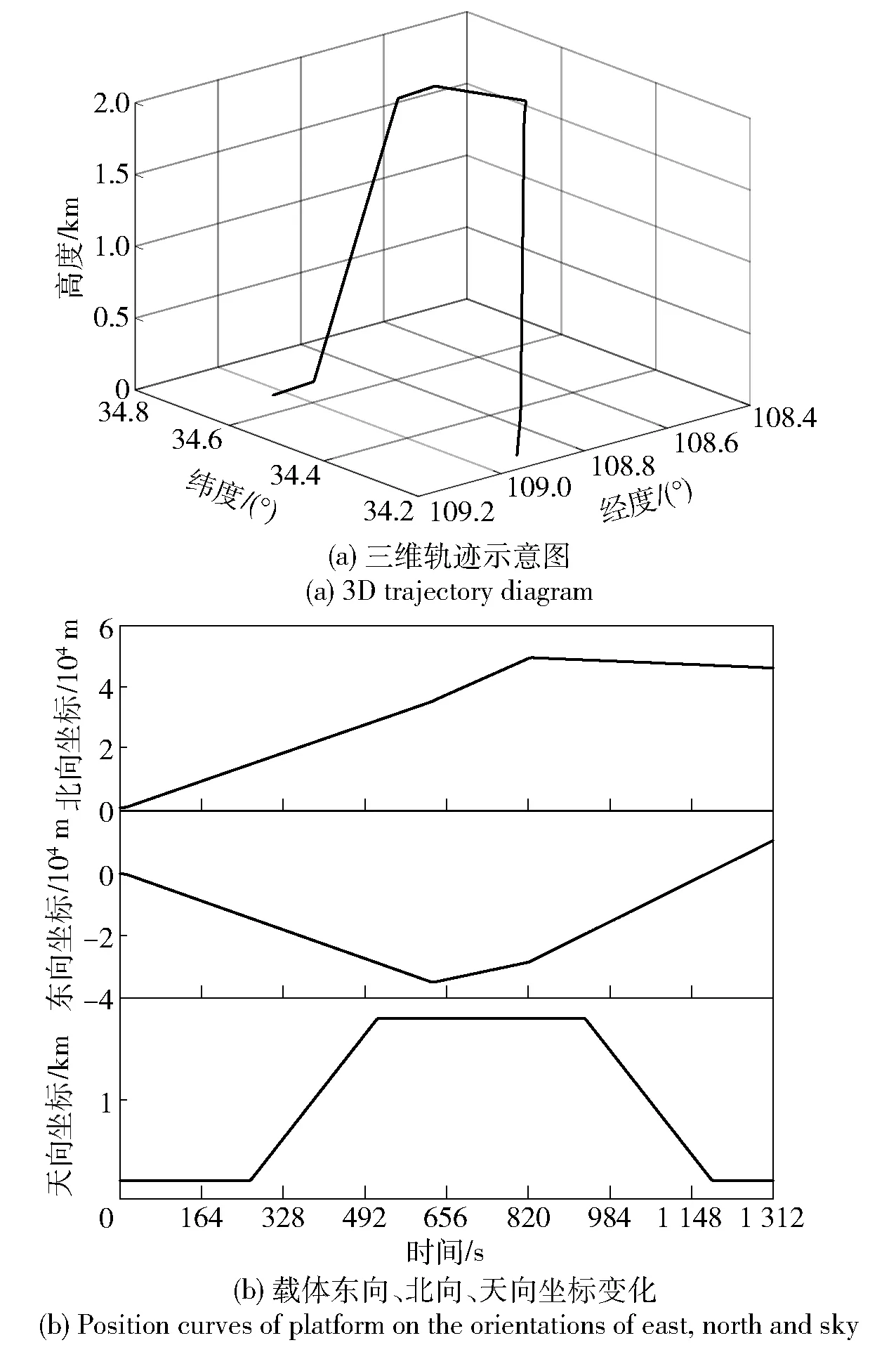
圖2 載體運動軌跡圖Fig.2 Trajectory diagram of platform

在仿真測試中，共產生了1 312 s的載體軌跡，軌跡中包括加速、減速、上升、下降、轉向等多種載體運動方式，如圖2所示為所產生的載體三維軌跡圖和東向、北向、天向軌跡曲線。根據載體軌跡分別模擬產生了INS輸出、GNSS輸出、LiDAR導航系統輸出和磁力計導航系統輸出，各模擬導航源的詳細規格如表1所示。為了驗證各算法對導航源變化的處理性能，需要在各個子導航源中模擬觀測量狀態變化過程：對于LiDAR系統而言，軌跡中載體的上升與下降過程會導致LiDAR系統中用于地圖匹配的特征點數量、匹配準確度下降，從而影響輸出的載體位置精度[3]；對于GNSS與磁力計則人為地分別在特定時間段加入了偏置與噪聲。為了更好地驗證算法在不同子系統狀態變化情況下的性能，在仿真實驗中分別設置了兩種測試方案：在方案1中各個時刻內有且只有1種子導航源狀態發生變化，且變化方式均為突變；方案2中的子導航源狀態變化形式更加復雜，在同一時段內最多有3種導航源同時發生變化，且變化形式也包含突變和漸變兩種。表2展示了仿真實驗中兩種方案下各導航源的變化情況。在仿真測試中，分別應用本文所提出的IMAPFG算法、普通FG算法[10]、基于最大似然估計的因子圖(MLEFG)算法[22]和基于傳統最大后驗估計的因子圖(MAPFG)算法[19]對各個導航源輸出數據進行融合，并比較融合結果。由于最大似然估計需要較大的樣本空間才能得到較好的估計結果，對于MLEFG算法，每100個樣本值才對各導航源的分布狀態進行更新。在最大后驗估計中，由于加入了先驗信息，無需大量樣本也能得到準確的估計值。在MAPFG算法中，每10個樣本值就對導航源的方差和均值進行更新。IMAPFG算法的均值和方差是隨著窗的滑動進行的，在仿真中3種算法的窗的大小都被設定為10，即每當產生10個觀測值后進行因子圖數據融合。另外，為了更符合實際情況，初始化的各子導航源的協方差矩陣都與仿真的數據有所偏差。

表1 仿真測試中各導航源參數Tab.1 Specifications of navigation sources for simulation test

表2 仿真測試中導航源觀測值變化設置Tab.2 Setting of observation values

實驗測試中所用的載體平臺如圖3(a)所示，圖中手推車用于搭載Novatel GNSS天線，慣性測量單元 (IMU)和UWB無線電單元，所有傳感器都通過脈沖秒(PPS)信號與GPS時間同步。 UWB網絡由6個節點組成，UWB測量結果與GNSS測量結果由筆記本電腦記錄。實驗中UWB系統的輸出頻率為10 Hz， GPS系統的輸出頻率為2 Hz，磁力計輸出頻率為10 Hz，表3列出了實驗中所用IMU的具體規格參數。在實驗測試中，手推車在36 m×5 m的區域內進行折返運動，實驗時間約為1 500 s. 手推車的運動軌跡如圖3(b)中所示，實驗場景被選在了植被覆蓋的邊緣區域，在此區域內，IMU、UWB和磁力計的導航輸出保持穩定，但植被的遮擋會造成GPS系統的定位精度下降，或出現固定位置誤差偏置等問題。為了量化各融合算法對于處理子系統觀測狀態變化的性能，在實驗環境中，IMU、UWB與磁力計基本不受到外界因素的影響，因此觀測量有較高的準確度，故采用以IMU/UWB/磁力計3種導航源的標準因子圖估計軌跡作為導航狀態參考真實值，相比于應用實驗中標記的載體軌跡作為參考真實值，這樣的設置可以增加速度與姿態的定量對比，同時也避免實驗過程中由于人為操作帶來的誤差。之后分別應用不同融合算法計算得到IMU、UWB、GPS、磁力計4種導航源組合的估計軌跡，并與真實軌跡進行比較。在實驗測試中，用于比較的融合算法種類與仿真實驗中一致。

圖3 實驗場景Fig.3 Experimental scene

在仿真與實驗測試中分別用到了GNSS、LiDAR、UWB和磁力計4種子導航源。由于各子導航源的工作原理不同，輸出的導航觀測量與對應的量測方程也有所不同。以下分別介紹4種子導航源對應的量測方程。

對于本文中仿真和實驗所用的GNSS、LiDAR、UWB導航系統，輸出的觀測量都為載體的位置參數，因此這3種子導航源量測方程可分別表示為

表3 實驗測試中MEMs和IMU系統參數Tab.3 Specifications of MEMs and IMU for experimental test

(34)

(35)

(36)

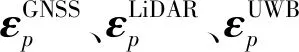
磁力計可以通過粗對準、坐標轉換、磁航向計算、四元數更新和循環計算磁航向等步驟輸出連續的載體姿態觀測信息。需要說明的是，磁力計在粗對準過程中需要利用加速度計測量值來簡單計算橫滾角以及俯仰角，之后對磁數據完成坐標轉換，并計算航向角；而在循環計算磁航向步驟中，磁力計仍需要從慣導系統中取得橫滾角和俯仰角才能完成磁航向的計算。雖然磁力計實際上只提供了航向角的觀測信息，但將測量航向角、橫滾角、俯仰角轉化為四元數后，則視為產生了四元數觀測值。

基于上述分析，磁力計的量測方程可表示為

(37)

5 測試結果和分析

在融合算法中協方差矩陣的跡可以用來表示觀測量的準確性，跡的值越小說明觀測量誤差越小，越可以信賴，反之則誤差越大，越不可信。圖4展示了在仿真測試方案1中，當分別應用MLEFG、MAPFG和IMAPFG 3種融合算法時，LiDAR導航系統協方差矩陣跡的變化曲線，圖中用A、B、C、D 4個區域標記了表2中定義的子導航源變化區間。從圖4中可以看出，MLEFG算法由于需要的觀測樣本大，對于LiDAR觀測量的估計與真實情況有較大延遲。而IMAPFG算法與MAPFG算法則能夠較為快速地對觀測量變化做出反應，且IMAPFG的協方差估計值更為穩定，曲線更加平滑，估計性能更好。特別地，當進入區域B時，受到GPS偏置的影響，3種算法對協方差矩陣的估計都出現跳變，但是由于IMAPFG算法能夠在迭代過程中實時更新均值向量，IMAPFG算法的協方差矩陣估計值受到均值變化的影響也較小，相應地，IMAPFG算法對GPS均值向量的估計也更加快速、準確。

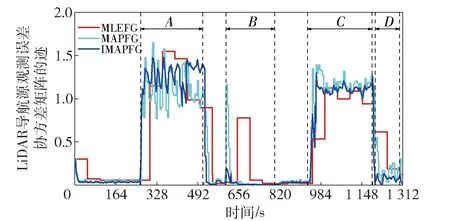
圖4 LiDAR導航源觀測誤差協方差矩陣的跡的變化曲線Fig.4 Trace curves of covariance matrix of LiDAR navigation observation error

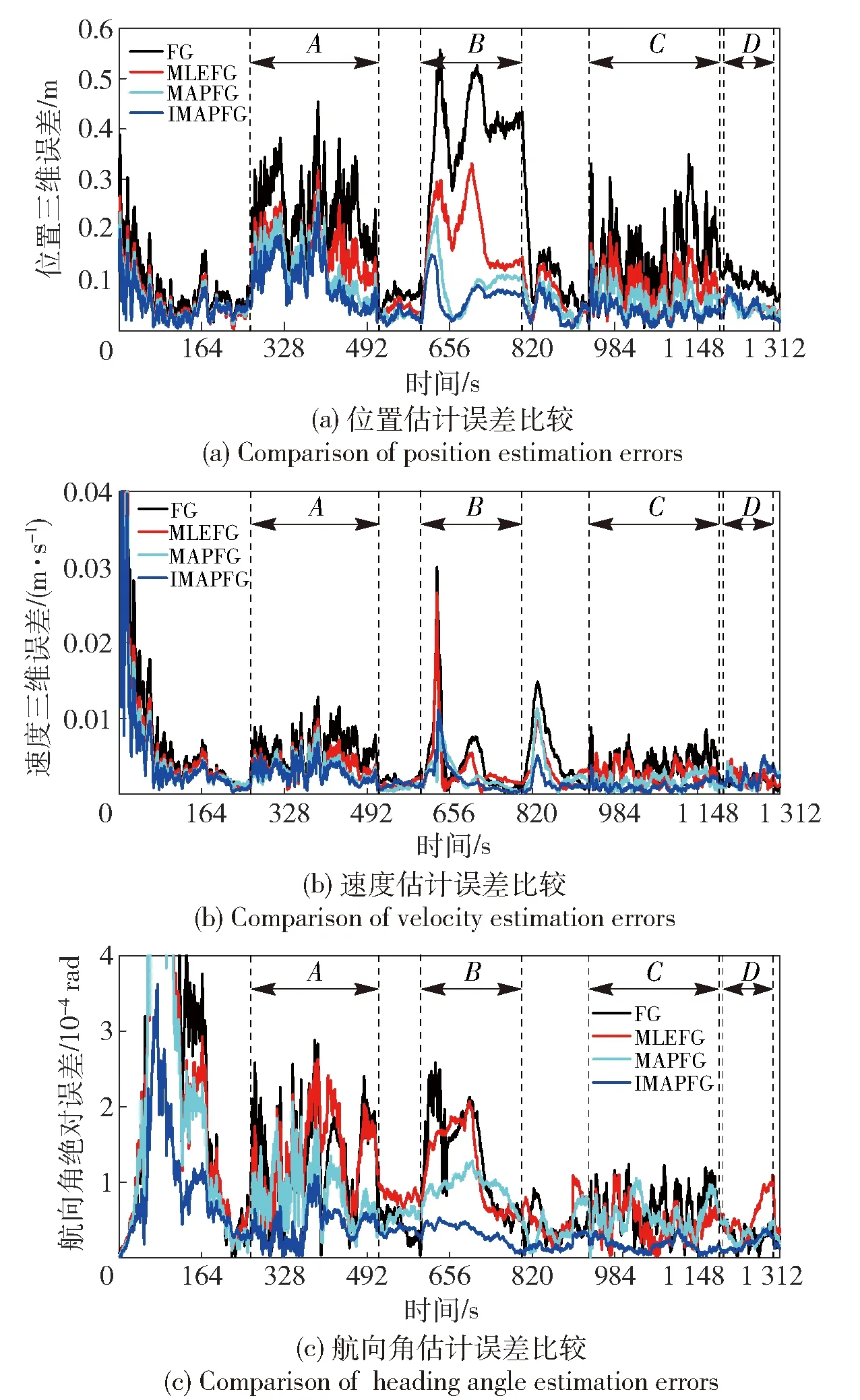
圖5 仿真測試方案1中各算法的載體位置、速度、航向角的估計誤差變化曲線Fig.5 Estimation error of the position, velocity and heading angle of algorithms in the simulation test of Scenario 1

如圖5所示為仿真測試方案1中應用不同算法得到的載體位置、速度、航向角的誤差變化曲線。從圖5中可以看出，在開始階段，各導航源相對穩定時，4種導航融合算法的性能差別較小。但是，由于在各個子導航源的初始方差中人為地加入了誤差，相比于傳統的FG算法，具有方差估計功能的其他3種融合算法對載體位置、速度、航向角的估計更加精確。隨著導航源狀態的變化，所有融合算法都受到一定程度的影響，各導航狀態估計值的精度均有所下降。其中FG算法受到的影響最大，且在各狀態各區域內，子導航源狀態變化所帶來影響并沒有隨著時間推移而減弱。相比于FG算法，其余3種算法都能逐漸降低子導航源變化帶來的影響。以區域A為例，當LiDAR導航源輸出的載體位置精度降低時，3種算法通過不同的方式逐漸提高LiDAR導航源的協方差值，從而在融合過程中減小對LiDAR導航源輸出數據的依賴。由于基于最大后驗估計的MAPFG算法與IMAPFG算法能夠更加迅速地對子導航源的變化作出準確反應，對導航狀態量的估計更加準確、受到子系統影響更小。進一步，由于在IMAPFG算法中，協方差矩陣和均值向量的最大后驗估計過程是在迭代過程中完成的，在每次導航狀態的估計中，殘差與子系統狀態信息相互影響，保證了估計值的最優性，從而使得每次對協方差矩陣、均值向量相比于MAPFG算法都更加準確。從圖5中也能看出，相比于MAPFG算法，IMAPFG算法對于子系統變化的反應更快，對導航狀態量的估計更加準確。

表4中定量地展示了4種算法在方案1中各個區域以及全部軌跡中導航狀態量的估計誤差情況。從表4中可以看出，相比于另外3種算法，由于缺少對各子系統觀測量狀態的更新，FG算法在A、B、C、D 4個區域內輸出的位置、速度和航向角的估計精度都明顯低于其他3種算法，而在整個仿真軌跡中，FG算法的平均位置誤差為0.17 m，平均速度誤差為0.57 cm/s，平均航向角誤差為，均為4種算法中最大。而IMAPFG算法，由于能夠對子系統狀態實時、準確地更新，從而能夠更好地應對子系統觀測狀態的變化或惡化，其平均位置估計誤差僅為0.05 m，相比于MAPFG算法、MLEFG算法、FG算法，IMAPFG算法的定位精度分別提高了28%、50%和71%. 除了定位精度外，IMAPFG算法的定速精度與定姿精度也有顯著提高。

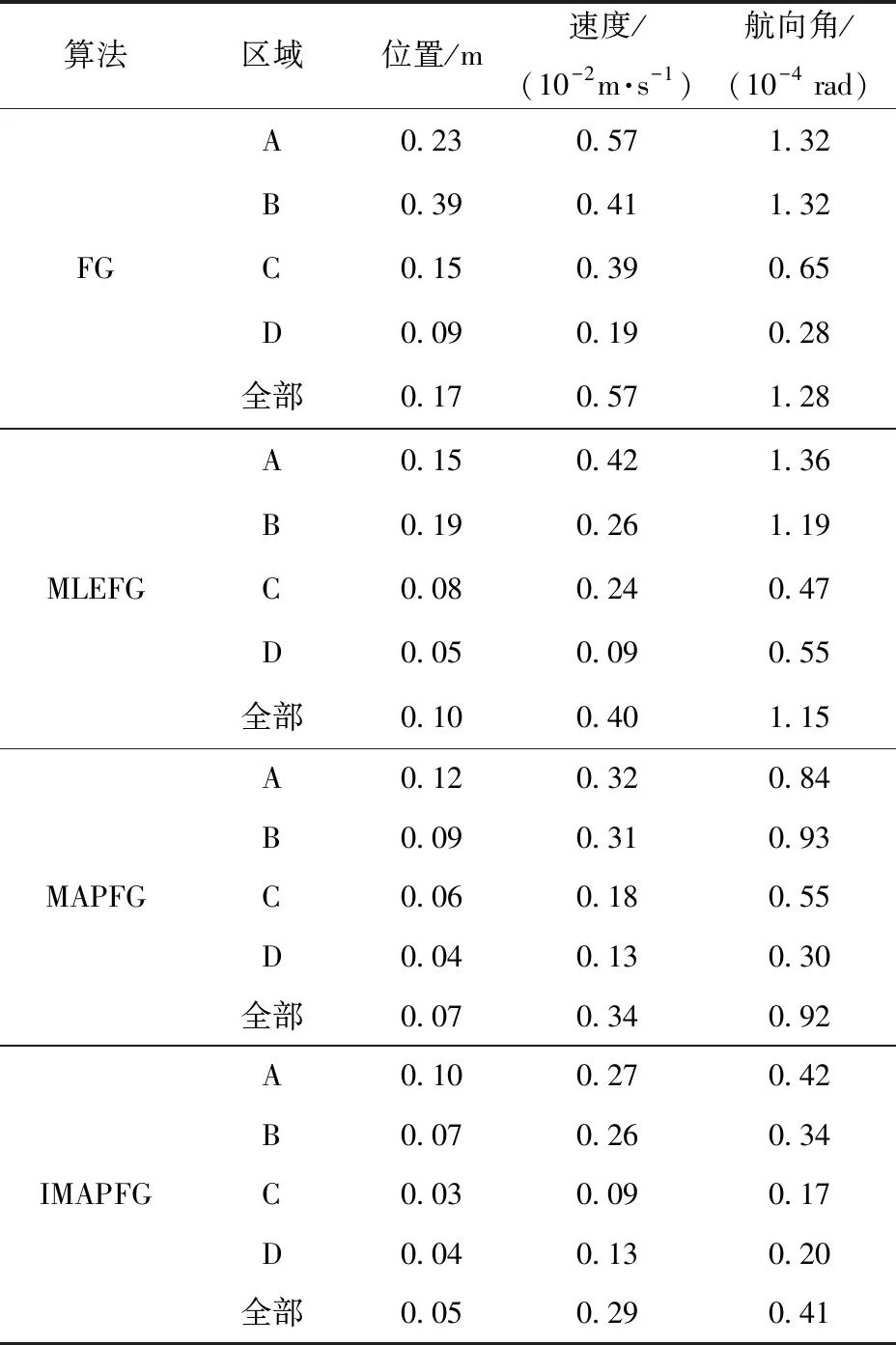
表4 仿真實驗中各區域以及全部軌跡中導航 狀態量的估計誤差Tab.4 Estimation errors of navigation state in different regions and whole trajectories in simulation experiments

圖6 仿真測試方案2中各算法的載體位置、速度、航向角的估Fig.6 Estimated errors of position, velocity and heading angle of algorithms in Scenario 2

圖6中展示了仿真測試方案2中應用不同算法得到的載體位置、速度、航向角的誤差變化曲線。橫向對比圖5中各個算法的導航誤差結果可知，圖6中更為復雜且持續時間更長的子系統時變狀態導致各算法的最終導航精度都惡化較多，特別是在有多個子導航源同時產生變化的H區域內時。但縱向對比各算法之間的性能可以看出，由于對仿真中GNSS子系統均值向量和協方差矩陣更加準確地估計，IMAPFG算法在各種導航狀態的估計都更加準確。在方案2中，IMAPFG算法輸出的位置三維誤差均值、速度三維誤差均值和航向角無誤差均值分別為0.13 m、0.4 cm/s和4.8×10-5rad. 在方案2中，相比于MAPFG算法、MLEFG算法、FG算法，IMAPFG算法的定位精度分別提高了31%、63%和86%.

在實驗測試中，如圖7(a)中所示為實驗測試中根據IMU、UWB、磁力計3種導航源估計得到的手推車運動軌跡，在實驗中將該軌跡視為真實軌跡。手推車在實驗人員的操作下在開闊區域與植被遮擋區域間做折返運動，遮擋區域如圖7(a)中陰影部分所示，圖7(a)中J、K紅色矩形框標記區域分別為開闊區域下軌跡和遮擋區域下軌跡，圖7(b)與圖7(c)分別為矩形框J、K標記區域的放大圖，圖中藍色圓點表示GPS的載體位置觀測值。從圖7中可以看出：在J區域下，GPS的測量值與軌跡基本保持一致，且抖動較小；而在K區域下，受到植被遮擋的影響，GPS輸出的位置觀測值受到較大影響，相比于區域J，可以明顯看出區域K內GPS的觀測值抖動更大且伴有一定的偏置。

表5中定量地展示了應用不同算法計算得到的IMU/UWB/GPS/磁力計多源組合導航系統的導航狀態量的估計誤差。從表5中可以看出，在開闊區域內，由于能快速、準確地估計子導航源的觀測精度，IMAPFG算法擁有最小位置、速度、航向角估計精度。而相比于開闊區域，4種算法在經過遮擋區域時，導航精度均有所下降，這主要是由于GPS觀測值在遮擋區域內惡化而引起的。但是，相比于其他3種算法，IMAPFG算法的定位精度惡化程度最低，IMAPFG算法的定位精度僅下降了18%，而對于MAPFG、MLEFG和FG算法而言，定位精度分別下降了28%、29%以及31%. 橫向比較各算法的導航精度可以看出，IMAPFG算法在整個實驗測試軌跡內擁有最優的導航精度，相比于MAPFG、MLEFG和FG算法， IMAPFG算法的定位精度分別提高了25%、59%、60%. 另外，除了定位性能外，無論在開闊區域還是遮擋區域內，IMAPFG算法的定速與定姿精度也均為最優。

另外需要說明的是，雖然在仿真測試中生成的INS與實驗測試中應用的INS精度相差近10倍，但是融合結果卻相差不多，這主要是由于更新頻率和子系統精度的差異引起，具體有以下兩點原因：一方面，實驗測試中采用UWB系統代替LiDAR系統，而UWB系統能夠提供更新頻率更高的子系統觀測量(10 Hz);另一方面，在實驗測試中采用INS、UWB、磁力計3種導航源應用標準FG算法計算得到的融合結果作為參考真實值，而當再次使用以上3種導航源數據作為觀測量時，就使得它們的測量值與視為參考真實值的導航結果較為接近，即相對精度更高，因此導致相對于該參考真實值的導航精度較高。

表5 實驗測試中各算法性能比較Tab.5 Performance comparison of the algorithms in the experimental test

6 結論

針對傳統多源組合導航因子圖融合算法精度受到觀測量噪聲時變特性影響的問題，本文提出了一種基于迭代最大后驗估計的IMAPFG算法，為了評價算法的性能，分別設計了仿真測試與實驗測試對算法進行驗證，并將測試結果與FG、MLEFG和MAPFG算法進行比較。所得主要結論如下：

1)仿真測試結果顯示IMAPFG算法能夠對子系統狀態變化做出快速準確的反應，相比于FG、MLEFG和MAPFG算法，IMAPFG算法輸出的定位精度分別提高了28%、50%和71%.

2)在實驗測試中，無論在開闊區域還是植被遮擋區域，IMAPFG算法的定位、定速、定姿精度均為4種算法中最優。

3)本文所提出的IMAPFG算法能夠有效提高子系統觀測狀態變化時的多源組合導航估計精度。