基于上海市地理國情成果的學生就學可達性測度與學區優化分析

李淑瑤，忻靜

(上海市測繪院，上海 200063)

1 引 言

隨著我國經濟社會的高速發展，我國的基礎教育水平顯著提高、教育實力得到了大幅度提升，但是由于各區域之間的教育水平存在差異，部分地區依然存在教育資源不均衡的情況。

地理信息系統技術大量應用于資源管理、環境監測、城市規劃、土地管理及交通、水利、林業等領域，在教育領域也得到應用。

近年來，國外很多學者利用GIS對學校與社區整體規劃、學校布局的優化調整，學區優化模型、交通成本與學區劃分兩者之間的關系等進行了深入的研究。20世紀80年代初，GIS開始應用于教育地理研究，美國華盛頓于1994年舉行了“全國GIS在教育中的應用”(簡稱EAGIS)會議，會議上討論了EAGIS的開發前景和展望。Taylor G等(1999)利用GIS對北卡羅來納州約翰斯頓縣的學校和社區進行了整體規劃，成功降低了交通對入學的影響程度[1]。Caro F等(2004)提出了一個基于GIS的學區布局優化模型，并以美國費城的學區為案例進行模型的驗證，認為結合定性分析與定量分析能夠有效地解決學區劃分的問題[2]。Hanley等(2007)對艾奧瓦州學校進行了調研，采用GIS技術分析了交通成本與學區劃分之間的關系，并計算了學區合并對交通成本的影響[3]。

國內將GIS應用于學校布局的研究相比于國外相對較晚。目前國內教育設施空間布局的研究主要集中在教育設施布局規劃、優質教育資源的配置、入學可達性以及學校規劃調整方面。2004年我國著手研發了“北京市教育資源布局電子地圖”，構建北京教育地理信息系統，為北京學校布局決策提供科學依據。孔云峰(2012)以就近入學為目標，構建學區劃分優化模型，利用線性規劃算法和GIS技術對中小學的學區進行了最優劃分[4]。周子懿(2015)通過采用GIS技術對比控規單元和學區劃分所形成的不同空間層次對小學的供需狀況和可達性水平的影響，進而說明學區劃分對小學實際服務能力的影響[5]。

上海市作為我國的超大型城市，無論是經濟總量、人口總數還是城市規模都處于領先地位，而龐大的城市規模和復雜的城市背景也必將導致城市管理和轉型升級方面充滿難題。在教育資源配置方面，上海選擇分區劃分學區的方法進行管理，其他大型城市也多選擇此種方法管理教育資源。可達性反映了服務區位與供需平衡的關系，是資源配置合理性評價的重要參考，城市的發展對學區優化提出了更高的要求。因此，在學區對口的前提下判斷小學可達性，確定更優的學區劃分方案，是大型城市進行教育資源均等化分析的必要內容。

在現有研究的基礎上，本文在ArcGIS平臺下利用多種方法，根據小學與居住小區之間的空間位置與小學資源現狀，實現小學可達性的量化評價，進行學區劃分優化探索，為大型城市中政府教育資源配置與管理提供參考。

2 研究區域及數據準備

2.1 研究區域介紹

普陀區以境內普陀路得名，故稱“普陀區”。位于東經121°39′，北緯31°25′，地處上海市中心城區西北部。東起滬太路、彭越浦、蘇州河與閘北區交界，南沿蘇州河、萬航渡路、長壽路、安遠路與長寧、靜安區毗鄰，西至滬寧鐵路、環浜與嘉定區接壤，北達真南路、薛家浜、靈石路與嘉定、寶山區相連。轄區內蘇州河東西穿越而過，距市中心人民廣場 7.5 km。總面積 55.53 km2，其中水域面積 1.65 km2。上海市普陀區街道劃分如圖1所示：

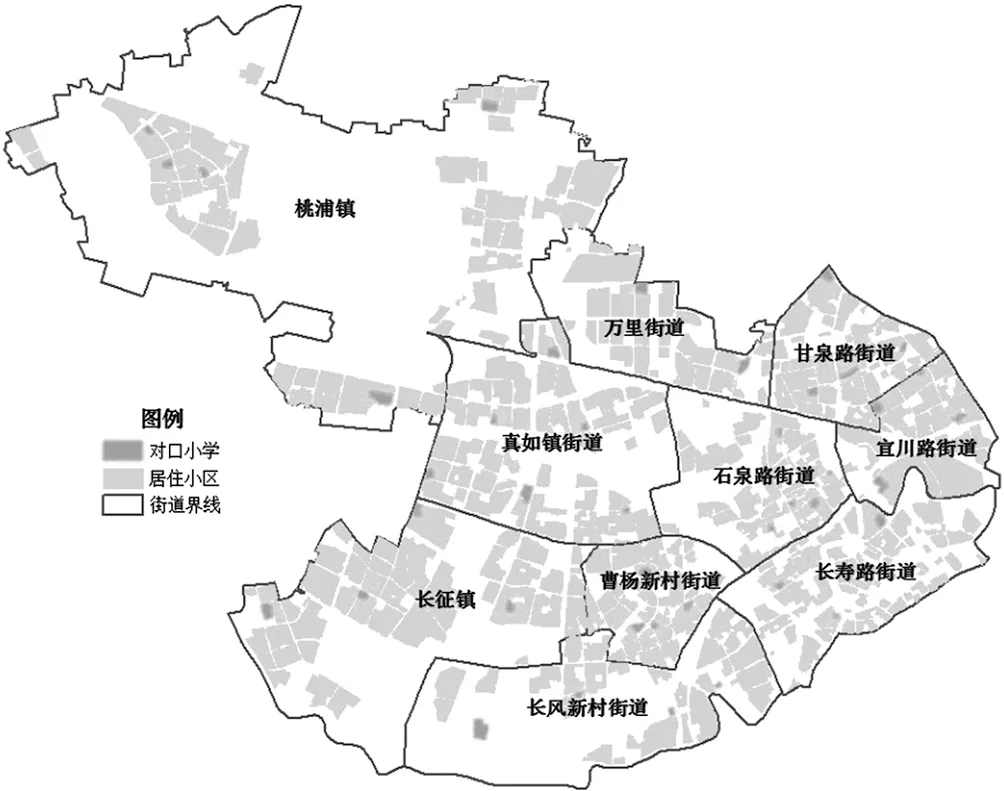
圖1 上海市普陀區街道劃分圖

普陀區的義務教育以公辦教育為主，區內民辦學校數量較少但辦學質量較高，能夠對優質公辦教育的短缺提供很好的補充。全區教育資源分布不均衡，優質教育資源集中分布在宜川路街道、甘泉路街道等東部地區，這些街道有著較好的教育基礎。而西部的桃浦鎮、長征鎮等地區屬于城鄉接合部，加之大量的人口導入，教育資源比較緊張。總體來看，全區有限的優質教育資源存量與不斷增長的優質教育需求之間的矛盾較為突出[6]。

2.2 小區與學校距離確定

研究小學教育資源空間布局的合理性，實現小學可達性的量化評價，必然是以小學至居住小區的交通距離為基礎的，而當前常用的距離多為歐式距離與路網距離，可較簡單地獲得對應數據，但是與實際的出行距離相差較大，并且只能據此估算出行時間。

本文選擇網絡交通大數據爬取的方法，獲取步行方式的出行距離(m)與出行時間(min)，利用真實的出行距離與時間，完成小學可達性的量化評價。

3 小區小學對口關系確定

與醫療、體育、文化、經濟等的可達性評價不同的是，教育有公辦學校學區劃分，即教育局公布招生地段表，對小區居民對口哪所公辦學校有十分明確的規定。

“學區制”是義務教育均衡發展體制和機制創新的實踐模式之一，是中小學實行分片劃區管理的制度。在學區內通過一定的管理制度、運行機制及考核評估措施，搭建交互平臺，實現資源共享，實施優質學校對薄弱學校在學校管理和教育教學上的指導與幫扶，以及教育設施設備、師資和生源的均衡分配，從而縮小區域內學校間的差距。這是一種中心拉動、以強帶弱、共同發展、整體推進的均衡發展策略。

因此對普陀區小學的可達性進行評價，必然是在保證其對口關系的基礎上進行的。即確定小區與小學的對應關系，一個小區對應一所公辦小學。在地圖中用連接線表示，如圖2所示。

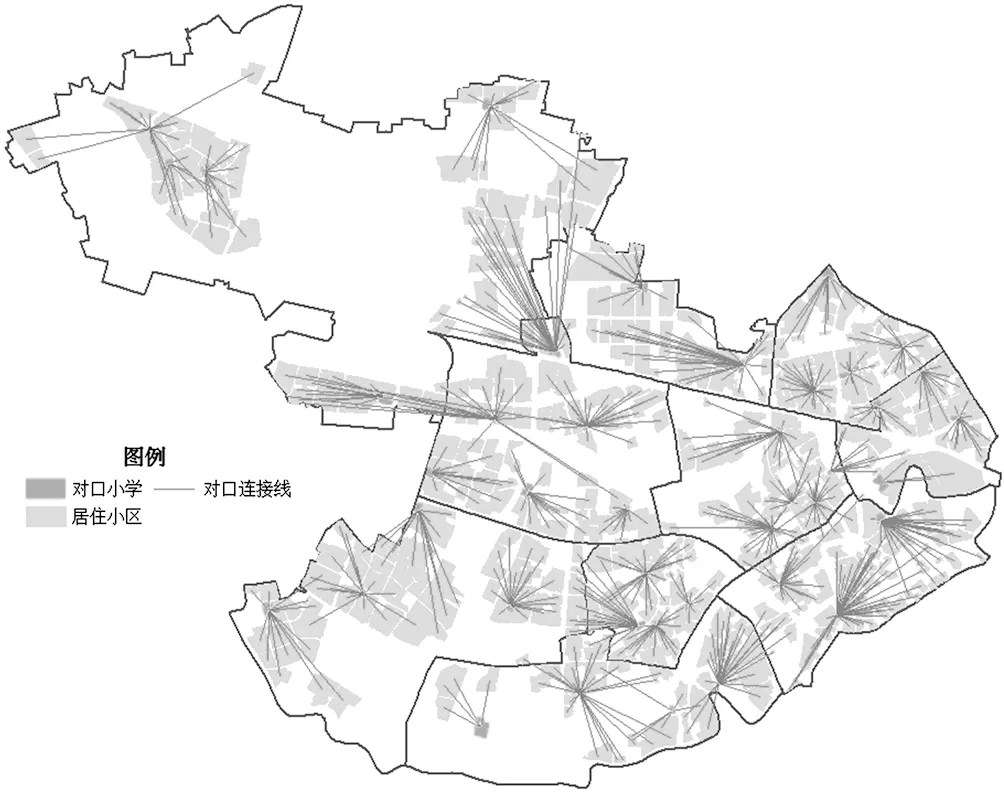
圖2 普陀區小區小學對口關系圖

4 小學教育資源可達性分析方法

4.1 基于交通大數據的最近距離法

可達性評價方法中最簡單的方法是最近距離法，就是以兩點間的距離為可達性指標，常用來計算所謂的“相對可達性”(lngram，1971)。最近距離模型主要是針對學生的就近入學距離進行比較，離最近設施點越近就代表可達性越好。該模型的數學公式為：

(1)

式中的D表示小學與居民點之間的距離；P表示國家標準規定，小學的服務半徑不宜超過 500 m。當比值大于1時，表示小區至小學的可達性不符合國家標準規定，比值小于等于1則表示可達性符合國家標準規定，空間布局相對合理。比值越小，可達性越好[7，8]。

4.2 結合重力模型的兩步移動搜索法

采用具有距離衰減系數的結合重力模型的兩步移動搜索法(G2SFCA)，從小區的尺度對普陀區小學進行可達性計算。考慮距離衰減作用，并將空間上供需雙方的空間效應隨距離衰減與供需雙方自身的引力規模結合起來衡量可達性水平，能更為全面準確地衡量居民獲取小學服務的難易程度[9]。

結合重力模型的兩步移動搜索法具體如下：

第一步，計算供需比R：

(2)

式中Rj為供需比，表示潛在人均小學服務能力；i為需求點(小區)，j為供給點(學校)；Sj為供給點的服務能力。Di為需求點的規模；k為搜索半徑內居住區地塊的數量；dij為需求點i與供給點j之間的距離；d0為搜索半徑；G(dij)為考慮到空間摩擦因素的距離衰減函數，計算公式如下：

(3)

第二步，計算可達性：

(4)

式中，αi為每個小區的可達性值；m為落在以i為核心，搜索半徑為d0的空間作用域內的學校數量；Rj為第一步計算的供需比。

4.3 熵權法確定學校得分

模型中的供給點(學校)通常選擇學生數、教師數等單一性指標來表征學校服務能力，以此判斷“供方”對“需方”的潛能大小，而學校服務能力通常是涉及多種因素的綜合表現[10～12]，因此本文中通過熵權法綜合學校各項指標得出綜合學校得分，作為學校自身的吸引力。選擇在校生數、畢業生數、招生數、班級數、教職工數、專任教師數、占地面積、校舍面積8個指標計算學校得分。

5 實驗與結果分析

5.1 基于交通大數據的最近距離法實驗結果

本文選擇網絡交通大數據代替歐氏距離，更加精準地反映可達性實際情況[13]。

《2017普陀區公辦小學招生地段范圍》中普陀區有對口信息的小學共41個。根據《2017普陀區公辦小學招生地段范圍》獲得小區與小學的對口關系，得到小區至對口小學的交通距離，基于交通大數據的最近距離法實驗結果如圖3所示：

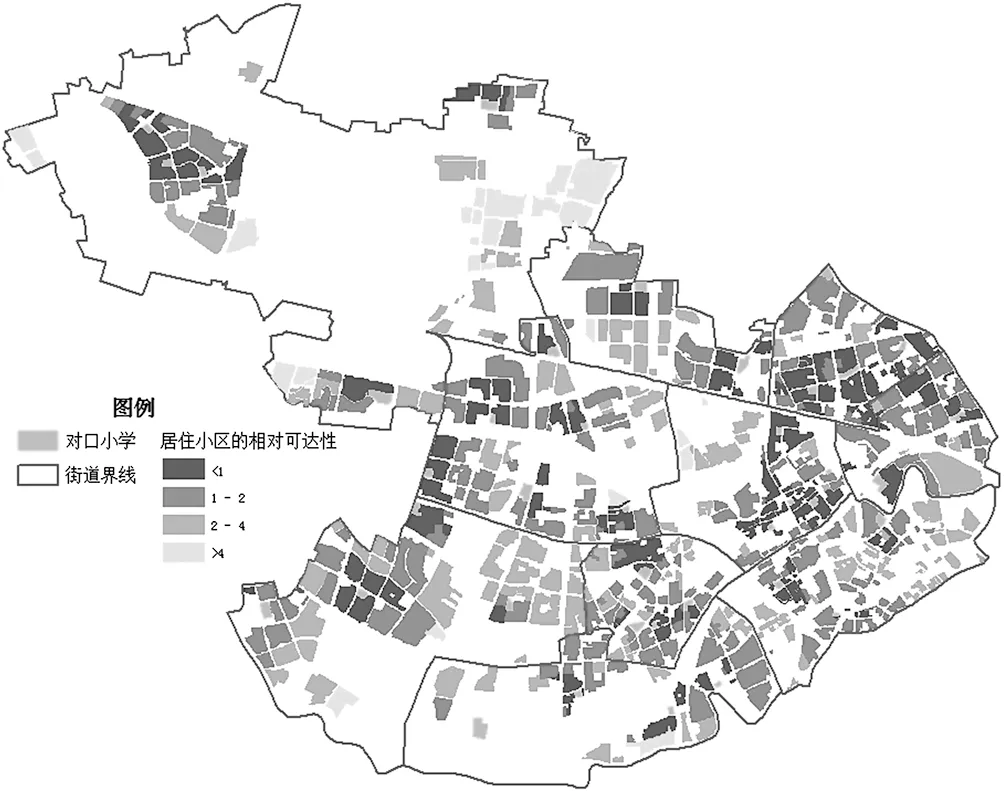
圖3 基于交通大數據的最近距離法相對可達性

普陀區小區共674個，其中符合國家規定，即至對口小學距離小于 500 m的小區共160個，占普陀區小區總數的23.7%。至對口小學距離小于 1 000 m的小區共429個，占普陀區小區總數的66.3%。

相對可達性數值越小，小區對應可達性越好。總體上看，普陀區相對可達性東高西低，與普陀區小區和學校東部密集的現狀一致。甘泉路街道與曹楊新村街道可達性整體較好，學生上學距離較近。

5.2 結合重力模型的兩步移動搜索法實驗結果

與傳統方法不同的是，由于上海的公辦小學存在學區劃分規則，按照居住小區分配不同學校，故原定以 500 m為搜索半徑計算供需比的方法，改為以對口信息為依據計算各小學供需比，即該小學對口的所有小區。

計算居住小區的空間可達性時，將原定的計算搜索半徑內所有小學對該小區的供需比與距離衰減函數乘積的和，改為計算該小區對口小學的供需比與距離衰減函數的乘積。

熵權法確定學校得分結果如表1所示：

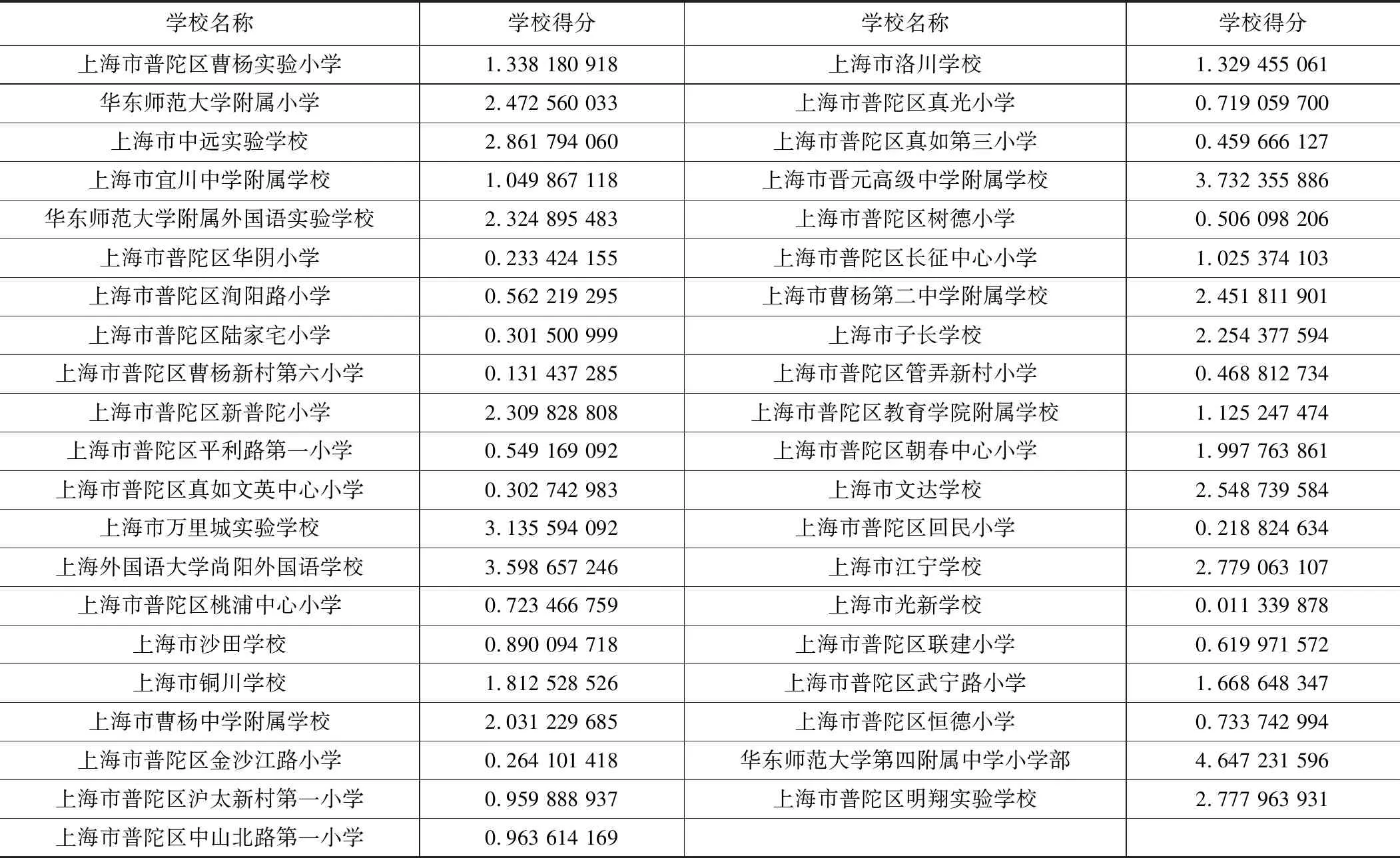
熵權法學校得分結果 表1

因此，結合對口信息與小區人口數據，可得小學供需比如表2所示：

學校供需比結果 表2

華東師范大學第四附屬中學小學部供需比比其他學校高很多，探究其原因，是該學校僅對口一個居委，且居委內小區適齡兒童人數極少(人口數據為2010年第6次人口普查數據，故可能時效性較低)。

計算得居住小區的空間可達性如圖4所示：

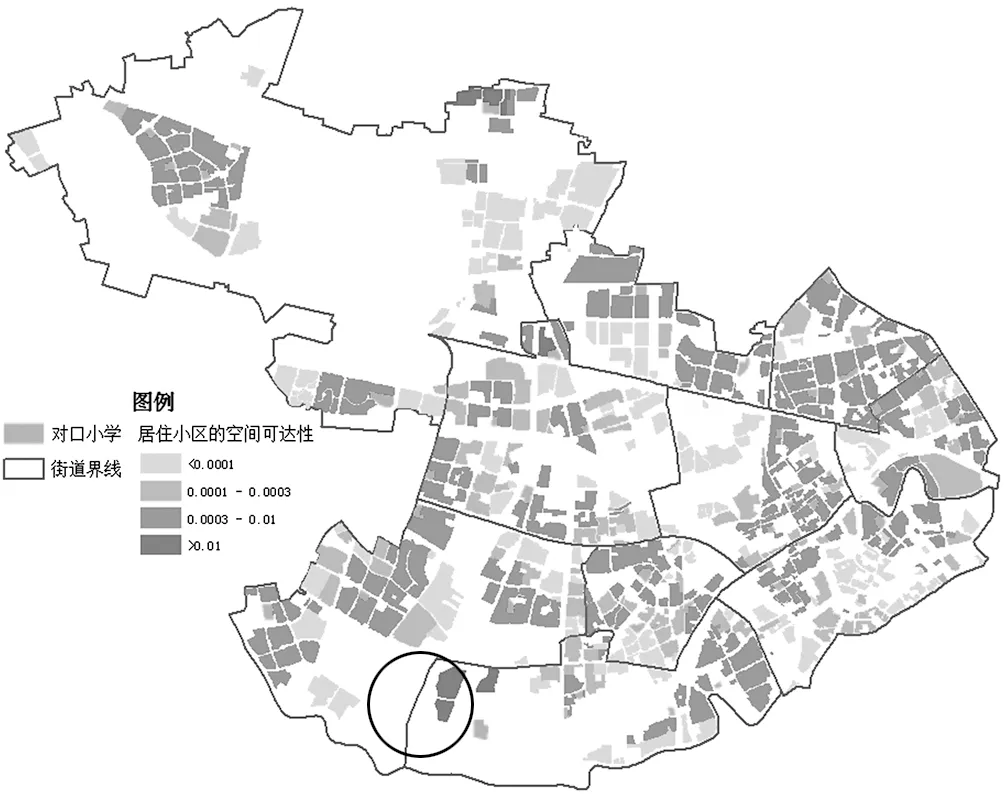
圖4 結合重力模型的兩步移動搜索法空間可達性

根據結合距離衰減函數的空間可達性來看，在普陀區各小區至小學的可達性差異較大，華東師范大學第四附屬中學小學部(橘色圈內)供需比比其他學校高很多，因此，在結合距離衰減函數的空間可達性研究結果中，該學校對口的小區可達性均屬于最高水平。從圖4中可以看出，甘泉路街道可達性均較高，長壽路街道部分區域與桃浦鎮部分區域可達性相對較低。

5.3 實驗對比

基于交通大數據的最近距離法實驗結果與結合距離衰減函數的小學空間可達性研究結果，有相似也有不同。

共同點是，兩個實驗結果中可達性整體趨勢相似，上海市普陀區可達性東高西低，與普陀區小區和學校東部密集的現狀一致，甘泉路的可達性均較好，長壽路的可達性均相對較差。

區別是，部分學校如華東師范大學第四附屬中學小學部等的周邊小區，由于考慮供需比，即學校的得分與小區適齡兒童人數等，表現出與最近距離法不同的趨勢，更加精準地反映各小區可獲得的小學教育資源現狀。

6 基于Huff模型的小學學區劃分優化方法

常用的Huff模型能夠計算出每個居民點到小學的可達性概率、小學對居民點的吸引力、潛在師生比、以及潛在服務學生數等，并對學校的服務區進行劃分，得到每個居民點學生就學的難易程度以及各小學擁有教育資源差異。Huff模型能夠較好地模擬出各個居民點上的學生在選擇不同學校時的不同入學概率，從而為學校的學區劃分提供客觀的依據。

在規劃布局已定的情況下，本研究旨在考慮如何通過合理的服務區劃分使得教育資源分配更均衡。如果一個社區的居民到某個小學就學的概率最高，意味著這個社區與該小學的相互作用最強，因此可以將這個小區劃到該小學的學區范圍。實現方式如下：

(1)根據網絡交通大數據，獲得普陀區各居住小區分別至所有普陀區內小學(含一貫制學校)的距離。

(2)計算每個小學對各個小區的吸引力

(5)

(6)

其中，Aij表示第j個小學對第i個居住小區的吸引力，Pij為第i個居住小區到第j個小學上學的概率。Sj為第j個小學的學校質量，dij為第i個居住小區到第j個小學上學的距離，即交通成本，β=2[14，15，16]。

(3)根據Pij篩選出對該小區吸引力最大的學校，即根據第i個小區的最大Pij值，j學校作為該小區的建議對口學校，從而確定基于Huff模型的小學學區對口關系。

7 基于Huff模型的小學學區劃分優化實驗結果

通過基于Huff模型的小學學區劃分優化實驗，獲得建議優化后的普陀區小學對口關系，如圖5所示，本文中Sj選擇5.2中熵權法學校得分來表示第j個小學的學校質量。

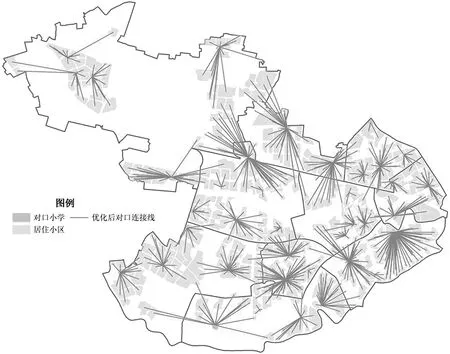
圖5 普陀區小區小學優化后對口關系圖

將圖2與圖5相對比，優化前與優化后對口關系發生了較大變化，根據網絡交通大數據，對優化前后學生入學距離進行對比分析，分析結果如表3所示：

優化前后學生入學距離對比 表3

對優化前后情況進行比較。結果顯示，優化后，所有小區到對應學校的距離總和由 621 255 m縮短至 598 429 km，整體優化幅度達3.6%；上學的最遠距離由 4 022 m縮短至 2 754 m，減少了31.5%；上學平均距離由 922 m縮短至 888 m，減少了3.7%；位于國家標準建議的小學 500 m服務范圍內的小區占比由23.7%增長至25.4%，增長了7%。

因此結合HUFF模型，篩選出對每個居住小區吸引力最大的小學，確定新的學區優化配置，從空間上看，對學生入學可以起到一定的優化作用，該方法可以為政府有關部門學區劃分決策提供可靠建議。

8 結 語

本文結合上海市公辦學校學區劃分的現狀特征，在傳統的教育資源可達性計算的基礎上，提出按照學區劃分判斷可達性的改進方法，即基于交通大數據的最近距離法與結合距離衰減函數的小學空間可達性計算方法，分別對上海市普陀區小學教育資源現狀與小區可達性進行評價，并對兩種方法進行比較。為相關部門進行選址規劃以及教育資源均等化配置等方面提供了有力的技術支撐。除此之外，本文在網絡交通大數據與學校得分的基礎上，通過Huff模型，對上海市普陀區的學區劃分進行優化，對比分析現狀與優化后學生入學距離，對優化結果進行客觀評價，為今后教育部門的學區劃分工作提供參考。但是，仍有部分內容，如熵權法計算結果作為供方服務能力是否需改進、實驗結果是否與普陀區各街道經濟發展水平等保持一致等等，有待進一步探究。