考慮通用件的備件多級配置優化研究?

董 琪 趙建忠 朱良明 隋江波

（海軍航空大學 煙臺 264001）

1 引言

備件由于種類眾多，故障模式和故障特點并非單一，僅依靠單一的維修模式或維修策略難以達到最佳的保障效果。因此，針對不同類型備件采取不同維修策略的實際情況，研究不同維修策略下的備件配置優化和庫存控制模型具有重要的價值和意義。隨著新裝備的不斷列裝，各種設備的組件通用化程度也逐步提高，有必要研究備件的通用性對其配置優化方案的影響。

修復性維修是備件維修普遍采用的策略，也是研究備件多級配置優化的重要對象，其研究的基礎來源于Sherbrooke提出的METRIC模型，理論基礎為靜態Palm定理［1～2］。盡管以該理論為基礎的多級配置優化研究非常廣泛，文獻［3～8］針對備件配置的高維、非線性、多目標、非固定分配等問題，分別從需求量擬合分布、目標函數構建、優化算法改進等方面進行了深入研究。但鮮有學者針對通用備件或通用備件的配置優化方案進行研究。文獻［9］通過引入備件重要度系統，建立了設備維修通用備件采購決策模型，但并未考慮多級庫存問題。在實際裝備保障過程中，通用件的比例呈逐漸增加的趨勢，在研究備件配置時，需要將該因素納入模型構建中，本文對現有多級配置模型進行改進，構建基于通用件的多級配置模型，利用邊際優化算法對模型進行求解，以得到供應保障系統最優配置方案。

2 考慮通用件的多級庫存模型

備件安裝在艦載系統的層次，可分為現場可更換單元（LRU）和車間更換單元（SRU），且存在考慮通用件的情況，即某SRU用于兩種（含）以上的LRU。當系統發生故障時，通過故障檢測確定造成故障的LRU，并進行換件維修，當艦員級儲備有該項備件時，則直接更換；反之，造成一次LRU短缺。艦員級對故障LRU進行故障定位，確定引起故障的SRU，若艦員級儲備有該SRU，則進行更換，并將已修復的該LRU送至相應級別的倉庫進行儲備；反之，造成一次SRU短缺。艦員級維修隊對故障的SRU具備一定的維修能力，若能修復，則將已修復的SRU送至相應級別倉庫備用；反之，則送至上一級站點維修，并向上一級站點申領一件SRU。若故障LRU無法在艦員級修復，則將其送至上一級站點，并申領一件LRU。備件維修和補給過程采取先到先服務策略，維修視為修復如新，不考慮報廢與橫向調撥的情況。與預防性維修策略不同，修復性維修針對電子類關重件，庫存策略為(S -1，S)，且故障的發生服從相互獨立的Poisson分布。

2.1 備件需求率模型

令備件 LRUj在站點m的需求率為 λj(n，m)，其中 m（m=1，2，…，M ）為保障站點編號，j=1，2，…，J 為備件編號，n（n=1，2，3）為保障級別編號，n=1表示基地級站點，n=2表示中繼級站點，n=3表示艦員級站點；LRUj所屬的第k項SRUjk的故障隔離率為 qjk(n，m)，k=1，2，…，K ，且設其中前z(z∈N+)項為z種通用件，其中，z=1表示所有LRUj所屬的SRUj1為通用件；z=0表示所有LRU內無通用件。艦員級站點m(m∈Echelon(N))對SRUjk需求率 λjk(n，m)：

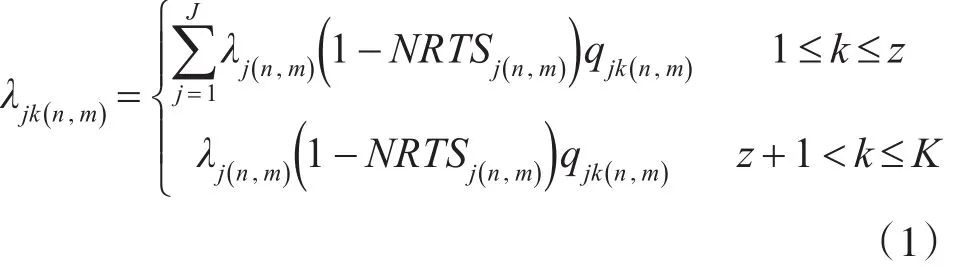
式中：NRTSj(n，m)為故障的 LRUj無法在站點m修復的概率。

其他等級的站點m(m ?Echelon(N ) )，LRUj的需求率為該站點所屬下一級別站點無法維修LRUj，并送至該站點進行維修的數量之和，即

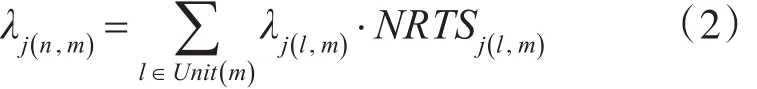
對于站點m(m ?Echelon(N ) )，SRUjk的需求率為接收所屬下一級送修的故障件，以及對該SRUjk上一層單元LRUj進行維修時所產生的對SRUjk的需求：

式中：NRTSjk()l，m為故障SRUjk在站點m下一級站點無法完成修復的概率；Unit(m)為站點m的下一級站點。

2.2 備件供應渠道均值和方差的修正

艦船裝備的可用度主要受備件短缺數的影響，而備件短缺數的大小與備件維修緊密相關，因此建模的關鍵是確定備件供應渠道的均值和方差。通過調研發現，該渠道包括：故障件在修數量、正在補給的數量以及維修延誤的數量［10］。

1）故障件在修數量

穩態條件下的任一時刻，站點m對故障LRUj和SRUjk的在修數量分別為

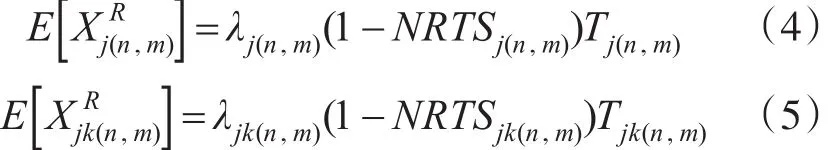
式中：Tj(n，m)和 Tjk(n，m)分別為故障 LRUj和 SRUjk在站點m的平均修復時間，且滿足：

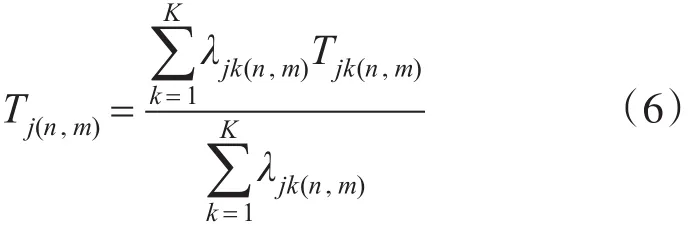
2）正在補給的數量

該部分等于由上級站點向站點m進行補給和處于運輸過程中的備件數量，以及上級站點現有庫存沒有所需備件而延誤補給的數量，即

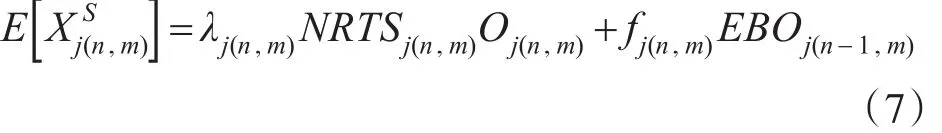
式中：Oj(n，m)為站點m向上級申請所需備件的延誤時間，fj(n，m)為站點m對應上級站點短缺數的比值，由下式可得

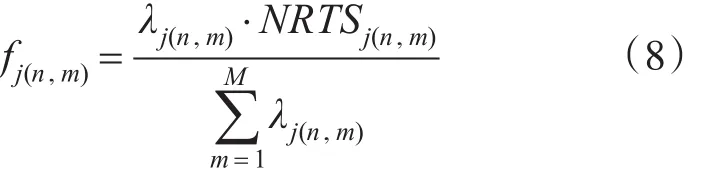
3）因SRU維修而造成維修延誤的數量

該值等于其包含 SRUjk短缺數 EBOjk(n，m)之和，即

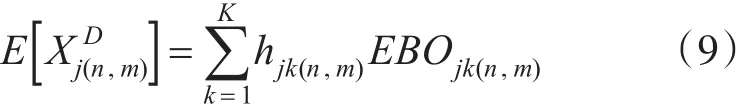
式中：hjk(n，m)為站點m維修 LRUj對SRUjk需求占SRUjk總需求的比值，即

當站點m向上一級站點申請備件時，上級對站點m補給造成延誤的概率服從二項分布。因此，站點m的備件LRUj供應渠道方差為Var[Xj(n，m)] ：

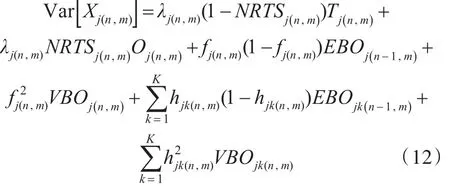
式中：VBOjk(n，m)為備件短缺數方差，具體計算方法見文獻［11］。

3 備件優化模型

衡量艦船裝備保障效能參數常用的包括裝備可用度（A）、滿足率（FR）、利用率（UR）、保障延誤時間（MLDT）等［12］。

由文獻［1］，結合裝備結構和多級庫存系統構成，得到裝備可用度為

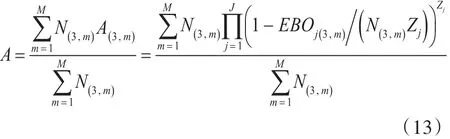
式中：Zj為LRUj的單機用數，N(3，m)為艦員級站點m保障的裝備數量。

備件系統滿足率FR為

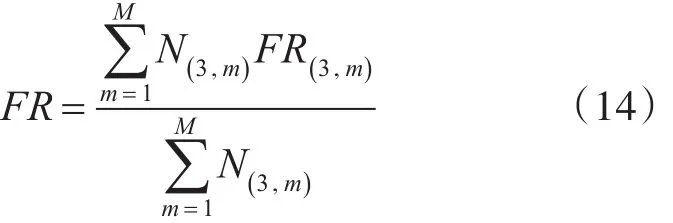
式中：FR(3，m)為艦員級站點m的備件滿足率，可由下式得到。

備件系統利用率UR為

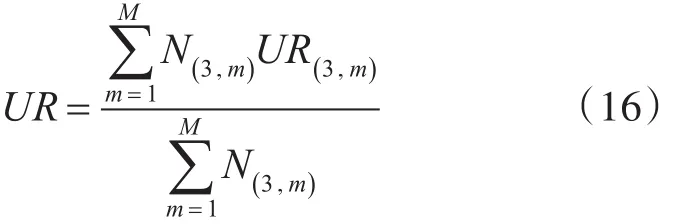
式中：UR(3，m)由文獻［13］計算得到。

備件系統保障延誤時間MLDT為

于是建立基于通用件的系統優化模型，即以費用為優化目標，以保障效能為約束：

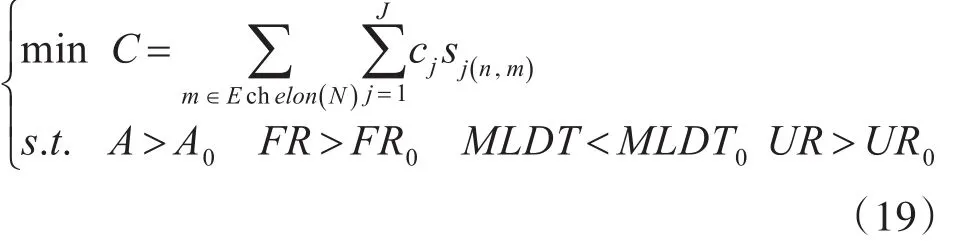
4 優化模型求解算法

邊際優化算法是求解備件配置費效優化模型常見而有效的算法之一，該算法的原理是通過比較各站點的備件邊際配置收益，確定備件的配置位置，并不斷迭代，直到滿足模型約束條件為止［14］。由于本節所建艦船裝備可用度模型是關于艦員級各項備件短缺數之和的函數，該目標函數具有可分離性，因此該目標函數具有凸性，通過邊際優化算法可確定每一步迭代的最優解［10，15］。考慮到可用度與備件短缺數的關系，可將求艦船裝備可用度的邊際效益值轉化為求艦員級各項備件短缺數的邊際效益值，提高算法計算效率。具體步驟為

Step1：初始化，令初始備件配置方案s為0；

Step2：由式（20），計算各級站點的各項備件配置量分別增加1所得的邊際效益值δj(n，m)：

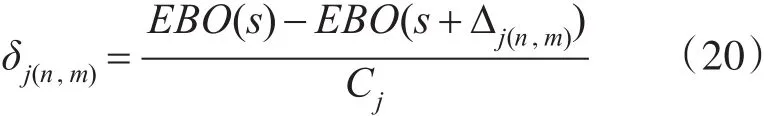
式中：EBO(s)為配置方案s下的艦員級站點備件期望短缺數之和，EBO(s+Δj(n，m))為在s方案基礎上，將(n，m)站點的第 j項備件配置數加1得到的艦員級站點備件期望短缺數之和，Δ=1；

Step3：根據Step2的結果，選擇 δj(n，m)最大值對應的站點備件，并令其配置量加1；

Step4：更新配置方案，并計算可用度、備件保障概率等指標是否達到約束要求，若未達到，則轉到Step2，繼續迭代；若滿足約束條件，則轉到Step5；

Step5：輸出備件配置方案。

5 實例分析

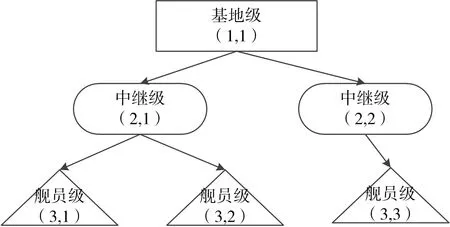
圖1 備件供應保障系統

平臺羅經是艦船的主要導航裝備，供應保障體系結構如圖1所示，該設備在三個艦員級站點的裝備數量分別為（12，10，8）。中繼級站點的采購延誤時間分別為8天和6天，艦員級站點采購延誤時間分別為4天、3天和4天。對該備件配置方案進行優化，得到滿足系統可用度為0.95的備件配置方案。

該設備主要由電源系統、控制箱、計算機和主羅經等組成，結構如圖2所示。

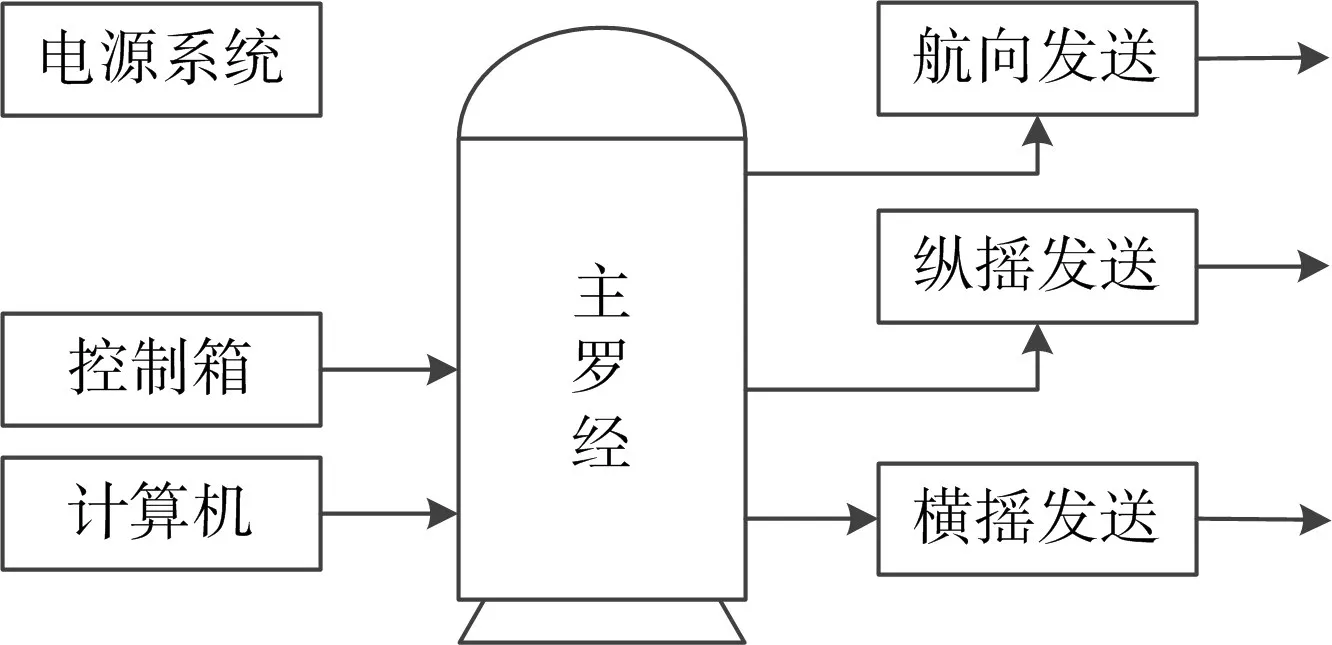
圖2 某平臺羅經結構圖

主羅經內部多為敏感元件，不易隨意拆動，該部件一般由生產廠家直接安裝于艦船，而不通過保障倉庫儲備，因此，本文選擇該設備的電源系統、控制箱、計算機的主要部件作為研究對象，具體參數如表1所示，其中+24V電源板為通用件，可在控制箱和計算機內通用，即SRU11=SRU21。相關維修參數如表2所示。

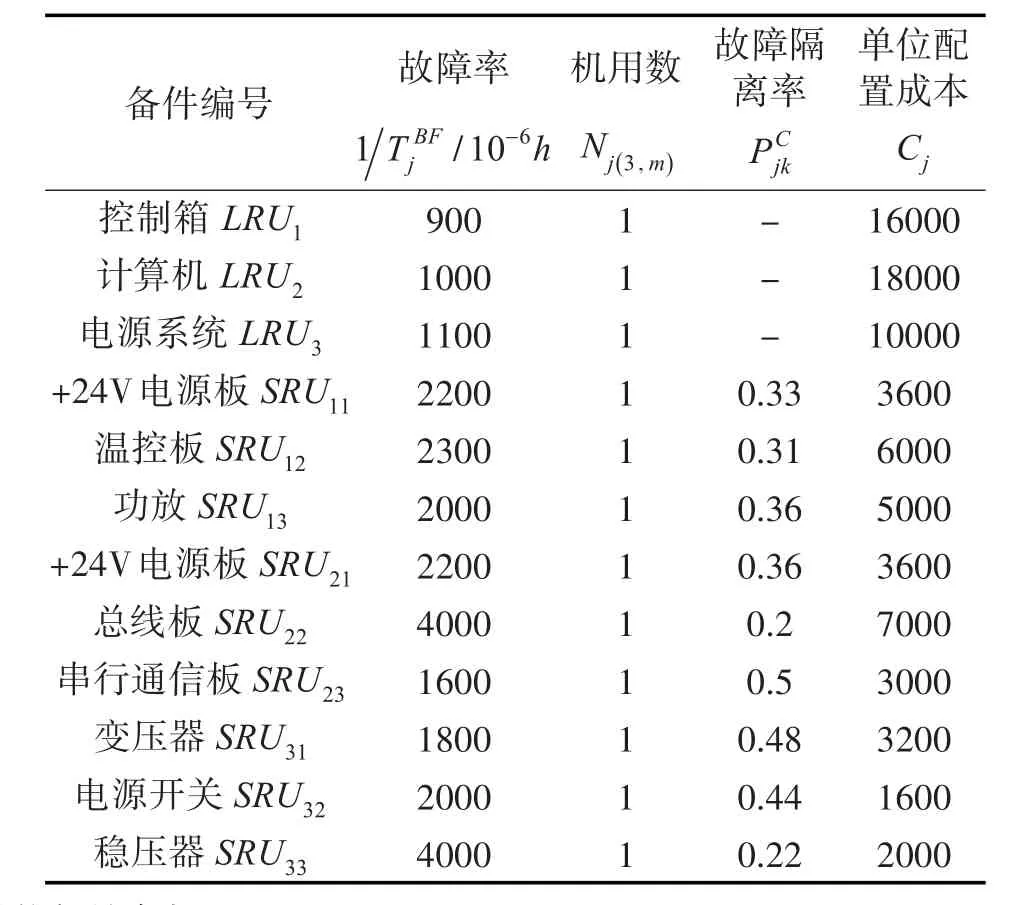
表1 艦船備件初始參數

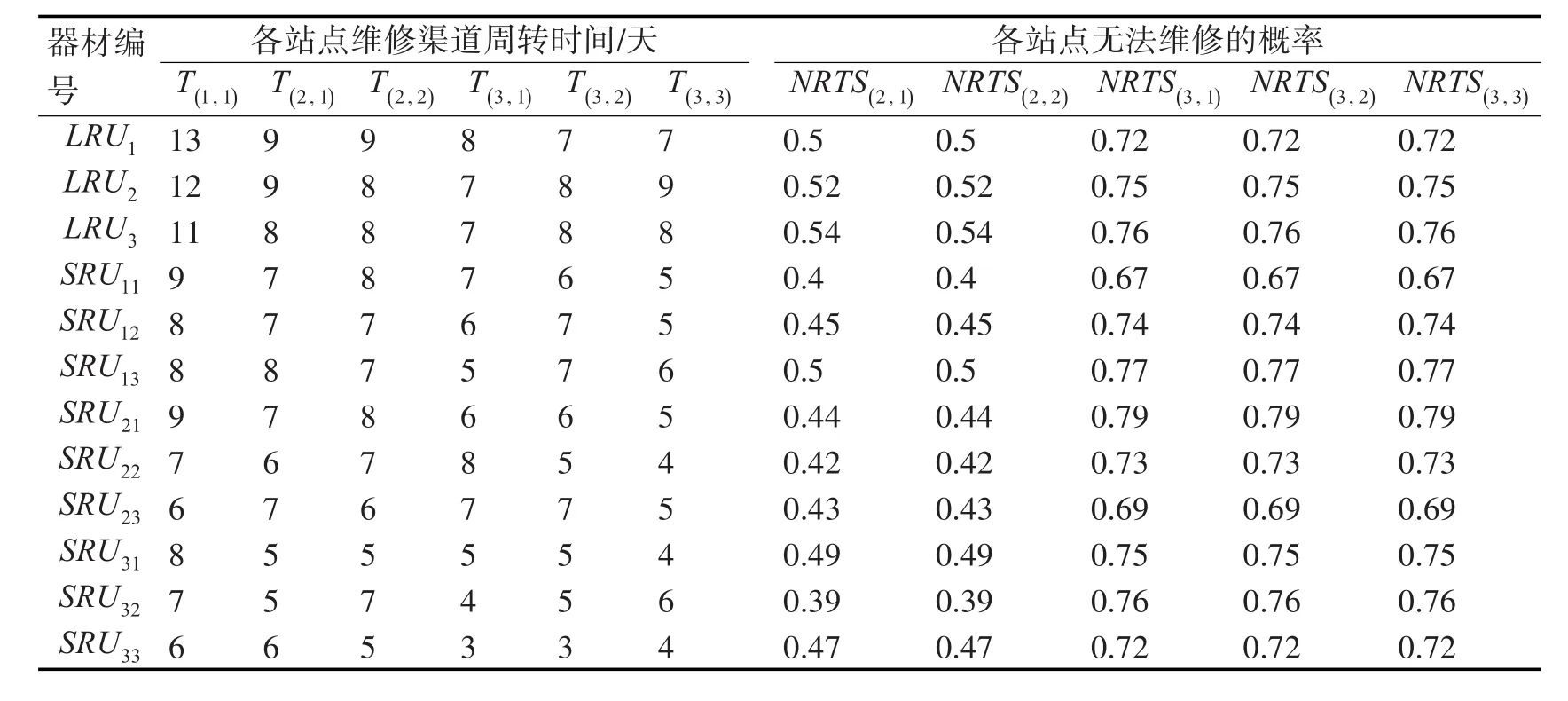
表2 備件維修初始參數

由邊際優化算法分別經66步和65步迭代，得到未考慮通用件情況的備件配置優化方案和考慮通用件情況的方案，分別如表3和表4所示，由GJB 4355《備件供應規劃要求》節現行籌措標準得到配置方案如表5所示。

表3 未考慮通用件的備件配置優化方案

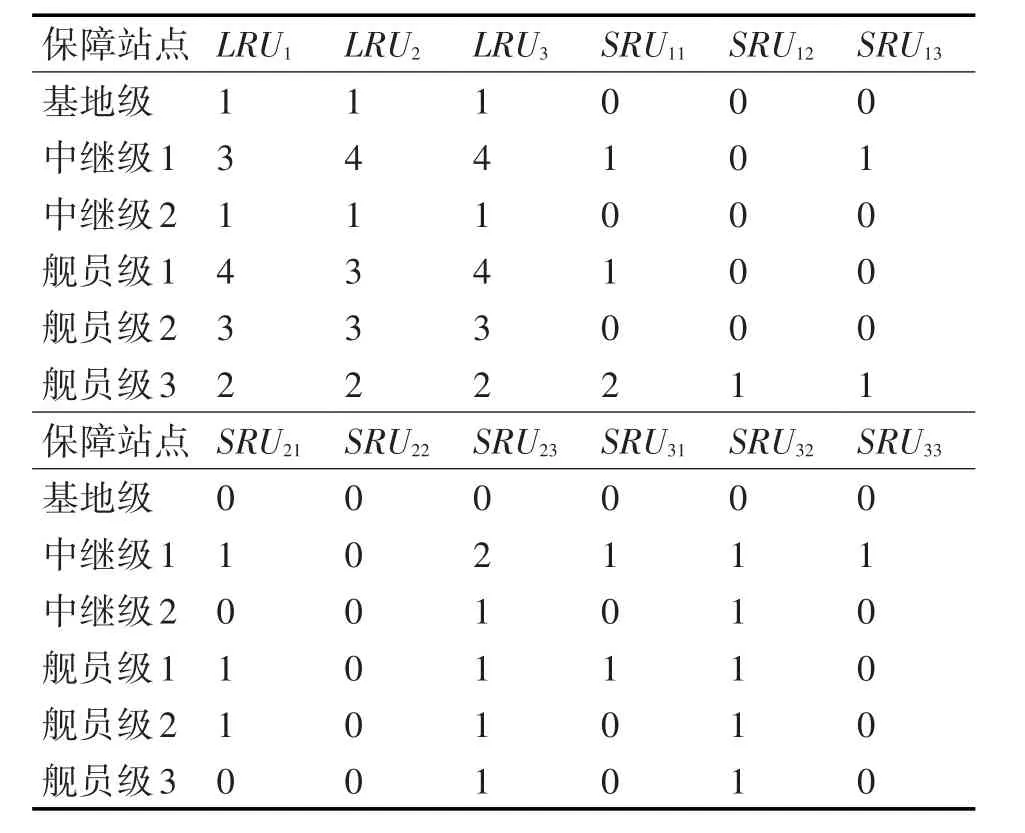
表3 考慮通用件的備件初始配置優化方案

通過對比表中數據，可得到結論如下：

1）配置優化方案主要以儲備LRU為主，且艦員級儲備的數量最多，中繼級其次，基地級最少；

2）考慮SRU11和SRU21為通用件的情況下，得到系統平均可用度為0.952、備件滿足率為0.892、備件利用率為0.463、平均延誤時間為14.087h、總費用為70.94萬元，在滿足可用度為0.95要求的庫存量為5件，小于將SRU11和SRU21作為專用件得到的優化庫存量6件，此時得到系統平均可用度為0.955、備件滿足率為0.897、備件利用率為0.465，平均延誤時間為13.359h、總費用為71.30萬元；

3）采用通用件是降低整體庫存，節約備件采購和管理費用，提高裝備可用度的重要手段。由于本文僅考慮了兩種LRU存在一種通用件的情況，因此所得對比結果差異程度有限，但隨著通用件存在的LRU種類越多，本節所研究模型的優勢將更加明顯；

4）根據GJB 4355《備件供應規劃要求》現行籌措標準所得配置方案在儲備數量上明顯多于本節研究得到的優化方案。這是因為，現行標準沒有將庫存系統內各站點作為一個整體進行考慮，缺乏有機的統籌，造成了備件配置數量的增加。因此，滿足約束條件的基礎上，本節研究配置優化模型的效果優于現行籌措標準。

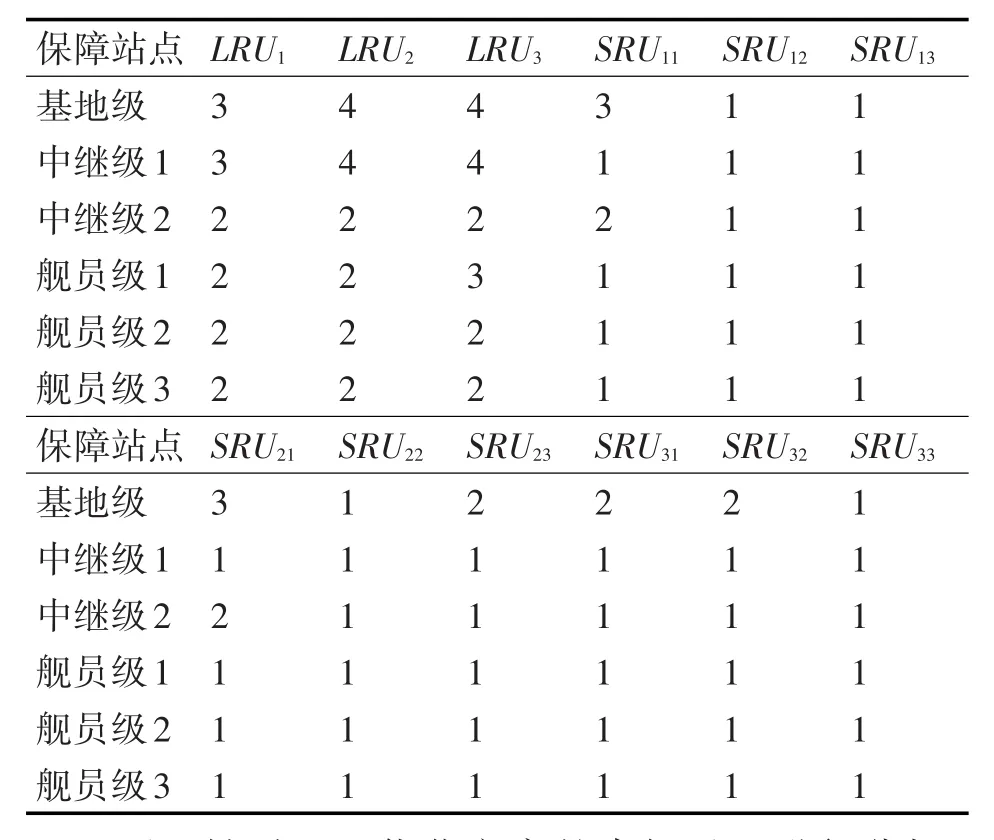
表5 現行籌措標準下的配置方案

下面針對配置優化方案的求解過程進行分析，得到邊際優化算法求解關于可用度和滿足率的費效曲線，如圖3所示。

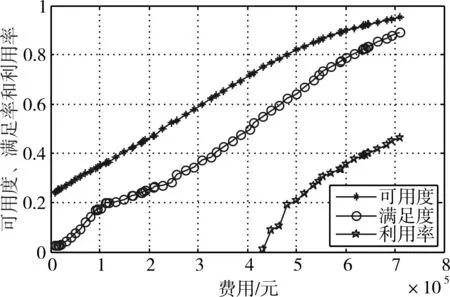
圖3 考慮通用件情況下的費效曲線

由上圖可知，可用度、滿足率和利用率隨費用的增加而呈非線性增加，其中可用度曲線具有凸性的特點，反映了邊際值隨迭代的增加而嚴格單調減少，由初始的0.0002遞減到1.23×10-5，如圖4所示；備件期望短缺數由初始的34.7857減少到1.4622，但每次迭代的減少量并非是嚴格單調遞減的，如圖5所示。

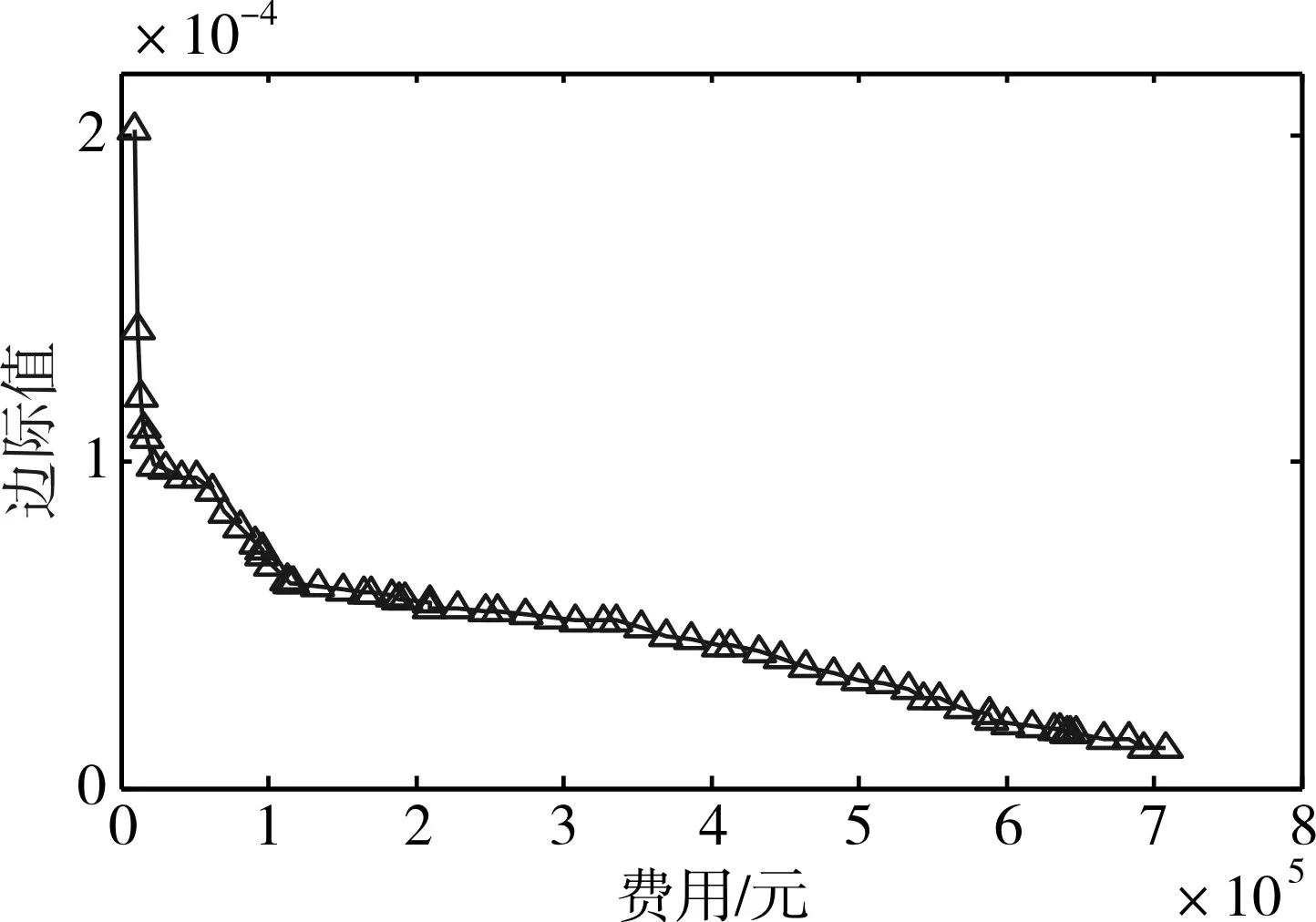
圖4 邊際值曲線

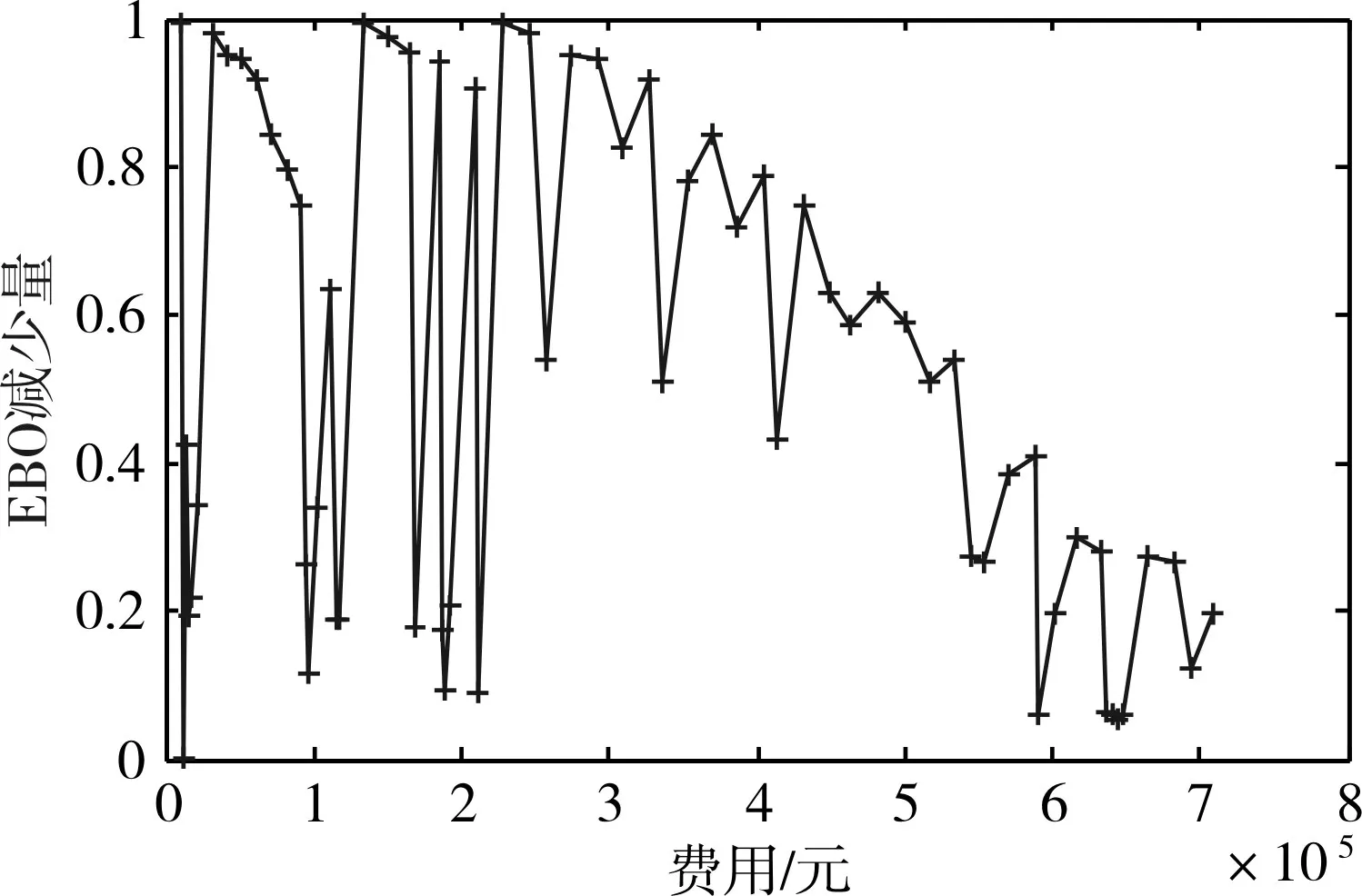
圖5 期望短缺數減少量曲線

圖6 所示為邊際優化算法求解關于延誤時間與費用的關系圖。

從上圖中可知，隨著費用的增加，備件配置數量也相應增加，延誤時間嚴格單調遞減，從初始的5134h逐漸減少到214h。

6 結語

對于平時備件供應保障中，多類設備存在通用件的問題，構建了基于通用件的備件配置優化模型。結合案例利用邊際優化算法所得結果表明：本文模型解決了原有模型評估裝備可用度存在偏高的問題，且節約了供應保障系統總庫存量，在滿足保障指標要求的前提下，提高了模型評估精度，降低了配置總費用，為目前裝備推廣使用通用性備件提供了理論依據和決策支持。