基于TOPSIS法的可再生能源發電績效評價

呂麗霞，齊秋妍

（華北電力大學 控制與計算機工程學院，河北 保定 071003）

0 引言

2016年12月26日發布的《“十三五”能源規劃》提出，到2020年把中國能源消費總量控制在50億噸標準煤以內，根據規劃目標測算，“十三五”期間單位GDP能耗應下降15%以上。為實現這個目標，除了做好煤炭的清潔高效利用這篇文章以外，繼續推進可再生能源的規模化發展也是未來工作的重點之一。2015年，中國風力發電累計并網容量達到12.9×104MW，全年風力發電累計上網電量為1.8×108MW?h。水力發電是目前建設規模最大，發電量最大的可再生能源，2015年中國水力發電裝機容量為31.9×104MW，年發電量為11.1×108MW?h。同樣是2015年，中國太陽能光伏發電和生物質發電的裝機容量分別為4.318×104MW和1.031×104MW，全年累計發電量分別為3920×104MW?h和5270×104MW?h[1]。中國可再生能源發電發展迅速，在可再生能源發電投資建設的規模方面居于世界前列。由于地理環境、社會環境、技術成熟度、環境友好度以及建設成本等因素的影響，中國各項可再生能源發電技術的發展情況不盡相同，對于風力發電、水力發電、光伏發電和生物質發電4項技術，在考慮資源量、占地需求、技術難度、對環境的影響、投資成本等指標的條件下，其發電績效如何，是本文將要討論的問題。

1 基于TOPSISI法的評價方法

1.1 TOPSIS法簡介

TOPSIS全稱technique for order preference by similarity to ideal solution，即逼近理想解的排序方法[2]。在一個多屬性決策問題中，分別假設理想解x*和負理想解x0，其中，理想解x*是虛擬的最佳方案，負理想解x0是虛擬的最差方案，然后將各備選方案與正負理想解的歐氏距離進行比較，最后據此得出各備選方案的優先序。

利用TOPSIS法求解多屬性決策問題概念簡單，易于理解，故該方法自問世以來得到了廣泛應用。由于各評價指標的重要程度不同，在采用TOPSIS法進行決策分析時需要確定各指標的權重，通常使用的方法有專家打分法、層次分析法等主觀法和熵權法、主成分分析法等客觀法。

1.2 方法步驟

1）建立指標矩陣

設有n個評價對象，p個評價指標（如p個評價指標中有逆向指標或適度指標，則將其正向化），得到原始指標矩陣如下：

式中，xij為第i個對象的第j個指標。

2）建立規范決策矩陣

由于各指標的量綱、變化范圍等有所不同，為了更好地反映實際的指標變化情況，需要對原始矩陣進行規范化處理，得到規范決策矩陣：Y={yij}。

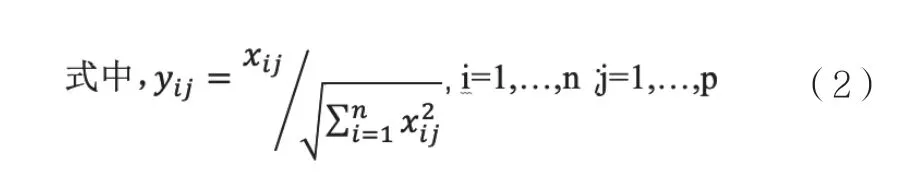
3）建立加權規范矩陣

設第j項評價指標的權重為wj，加權規范矩陣為R={rij}。

式中，rij=wjyij。

4）確定理想解與負理想解

由各項指標的最優值和最劣值分別構成理想解X*和負理想解X0。X*=(x1*, x2*,…, xp*)，X0=(x10, x20,…, xp0)。

5）計算各方案與正負理想解的歐氏距離

方案xi到理想解的歐式距離為：

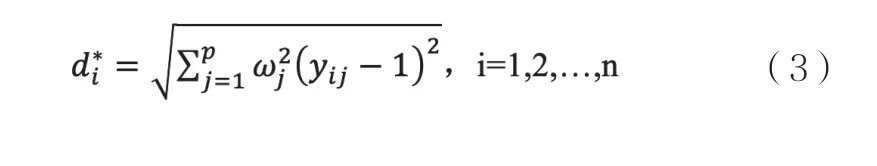
圖1 層次分析模型Fig.1 Hierarchical analysis model

方案xi到負理想解的歐式距離為：

6）計算各方案到理想解的相對接近度：

式中，di0為方案xi到負理想解的歐式距離，di*為方案xi到理想解的歐式距離。

7）按相對接近度的大小排序，ci*越大，表明方案xi越接近最優水平。

2 基于層次分析法的權重設置

2.1 建立層次分析模型

層次結構一般分為目標層、準則層、方案層3層，在本文中，可建立如圖1所示的層次分析模型。

評價的目的是比較幾種可再生能源發電績效的高低，故目標層為可再生能源發電績效的得分；準則層包括經濟、技術、資源以及環境幾方面因素；由準則層引出的具體指標包括發電成本、裝機容量、能源加工轉化效率等8個指標。模型的建立遵循任意兩個因素不重疊和每一層所列因素盡可能大地包含上一層全部內容兩個原則[3]。

2.2 構造判斷矩陣

根據專家打分結果構造一級指標判斷矩陣見表1。

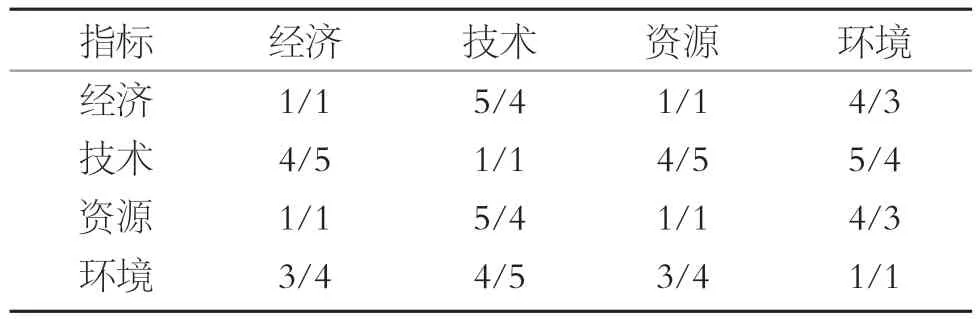
表1 一級指標權重判斷矩陣Table 1 First-order indicator weight judgment matrix

表2 隨機一致性指標RI的值Table 2 Value of the random consistency indicator RI

得到判斷矩陣：

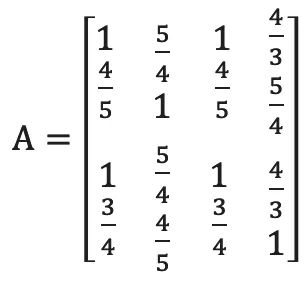
利用方根法，將矩陣A各行進行乘積并歸一化，得到特征向量：

W=[0.2814，0.2343，0.2814，0.2029]T

2.3 計算判斷矩陣的最大特征根

最大特征根 λmax=1/n∑i(AW)i/Wi= 4.003119。

2.4 一致性檢驗

CI為一致性指標，通過將CI與平均隨機一致性指標RI進行比較，可以檢驗判斷矩陣是否具有滿意的一致性。隨機一致性指標RI的值見表2。

CR=CI/RI，若CR≤0.10，則認為該判斷矩陣具有完全一致性，計算得到的權重系數Wi可以較好地反映上一級指標中各指標的相對重要程度；若CR>0.10，則需要重新考慮所建立的權重判斷矩陣[4]。

根據表2可以查出當階數為4時，RI=0.9，故CR=CI/RI=0.001156，CR<0.10，通過一致性檢驗。

同理，計算下級指標權重，最后得到可再生能源發電績效評價指標權重見表3。

3 可再生能源發電績效評價

3.1 建立指標矩陣

參考國內行業研究報告、國家發改委研究報告、中國科學院及科學技術部的新能源科技路線圖等資料，得到各項指標的值見表4，并得到原始矩陣X與規范化矩陣Y。

表3 可再生能源發電績效評價指標權重表Table 3 Weight table for indicators pf renewable energy power generation performance evaluation

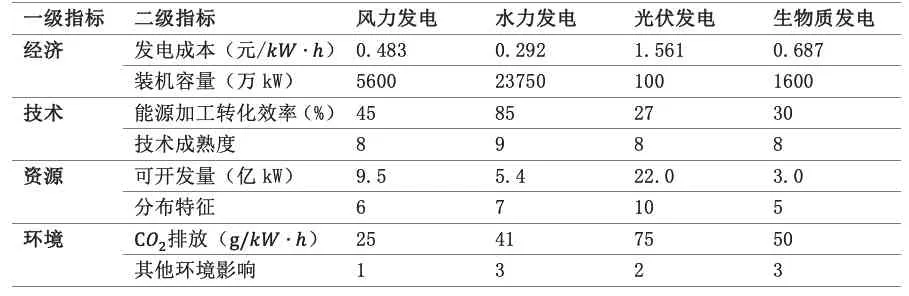
表4 各項指標賦值Table 4 Assignment of various indicators

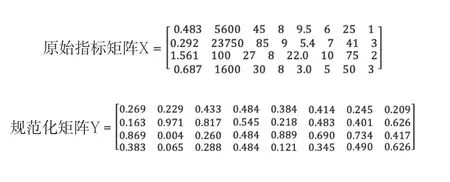
3.2 建立加權規范矩陣

根據已知的權重矩陣W與規范指標矩陣Y計算得加權規范矩陣R：

3.3 計算各方案到理想解與負理想解的距離

本文共有4個評價對象，理想解與負理想解分別為X*=(0,1,1,1,1,1,0,0)，X0=(1,0,0,0,0,0,1,1)，根據公式分別求得每個對象到理想解與負理想解的歐式距離：

3.4 計算相對接近度并排序

根據公式求得4個方案到理想解的相對接近度分別為：

按照相對接近度大小排序，可得最接近理想解的方案為水力發電，其次為風力發電和光伏發電，最遠離理想解的方案為生物質發電。

4 結論

本文將TOPSIS法應用于可再生能源發電績效評價中，在權重的確定上采用了層次分析法，建立了績效評價的指標體系，對水力發電、風力發電、光伏發電及生物質發電4種發電技術的績效進行了比較，從而可以清楚地看到這幾種技術的績效排序。本文在評價過程中盡可能做到客觀準確，但由于作者水平所限，文中可能存在不足之處，希望能對可再生能源發電的發展具有一定參考價值。