變截面輸流管道防共振可靠性分析

劉 慶,白雅潔,劉永壽

(1.中國飛行試驗研究院， 西安 710089； 2.西北工業大學 力學與土木建筑學院， 西安 710129)

輸液管道廣泛應用于航空航天裝備管路系統、裝甲車輛燃油/液壓管路系統、海上艦船油料補給系統等之中，且常常面臨著復雜的振動環境。因此，提高輸液管道動力學可靠性是武器裝備中亟需解決的重要問題。變截面錐形管是一種常見的輸液管道結構，如管道系統閥門的安裝處會采用錐形管與等直管道對接，噴嘴處采取變截面管道提高噴口流速等。由于管道輸流期間受到基礎振動、液體脈動等同時作用，且在實際工程中管道的幾何尺寸及物理參數在設計、制造過程中具有不確定性，因此輸液管道結構的激振力頻率和固有頻率不是定值,而是隨機變量。當管道的固有頻率與施加在管道上的外激勵頻率接近時，結構會發生共振，對管道造成嚴重的共振失效[1]。因此，對于管道的防共振可靠性設計有著很高的要求。

近年來，研究者對于等直管道防振動可靠性做了細致的研究。張屹尚等[2]通過Kriging代理模型研究了充液管道流固耦合作用下的非概率共振可靠性分析。李劍楠[3]等基于人工神經網絡模型，結合Monte-Carlo法對埋地管道在液化土地場、斷層場地等條件下進行可靠性分析。Ritto等[4]提出了考慮建模誤差的流體-結構相互作用的概率模型，將輸流管道的微分方程通過有限元方法離散化后得到降階模型，并以得到的隨機特征值分析了系統的顫動和發散不穩定模式。Alizadeh等[5]將蒙特卡洛模擬與有限元相結合，應用于輸流管道的概率自激振動和穩定性分析，對系統中流體參數隨機性效應與管道結構參數的隨機性效應進行了比較。但上述研究只停留在簡單直管道的可靠性研究，并未涉及復雜管道。在變截面管的自由振動方面，張子駿[6]給出了變截面管道輸送非均勻流的動力學控制方程，并研究了變截面管錐角變化對于管道動力學性質的影響等。但是將變截面管道的自由振動和防共振可靠性結合在一起的少之又少。

本研究將基于變截面管道的動力學控制方程，將動剛度矩陣法與主動學習的Kriging模型(ALK方法)相結合，考慮流體非均勻流動的作用，求解不同流速和截斷系數下兩端簡支的變截面管道的固有頻率，進而計算出管道的防共振失效概率，討論流體流動及截斷系數對變截面管道固有頻率和防共振失效概率的影響。ALK算法[7]是近年來新發展的一種精確高效的可靠度計算方法，其通過ERF學習方程“主動”挑選出最可能位于極限狀態平面附近的訓練點，加入到設計點中更新Kriging模型，通過不斷迭代直至滿足收斂條件。該方法運用到管道防共振可靠性的計算，可將激振力頻率上下界附近的點篩選出來加入到初選樣本點中，極大地提高計算效率，同時也能保證精度。本文的工作為變截面管道的防振動可靠性方面的研究提供參考，對于變截面管道的防共振設計和優化有著重要意義。

1 變截面管道的固有頻率

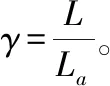
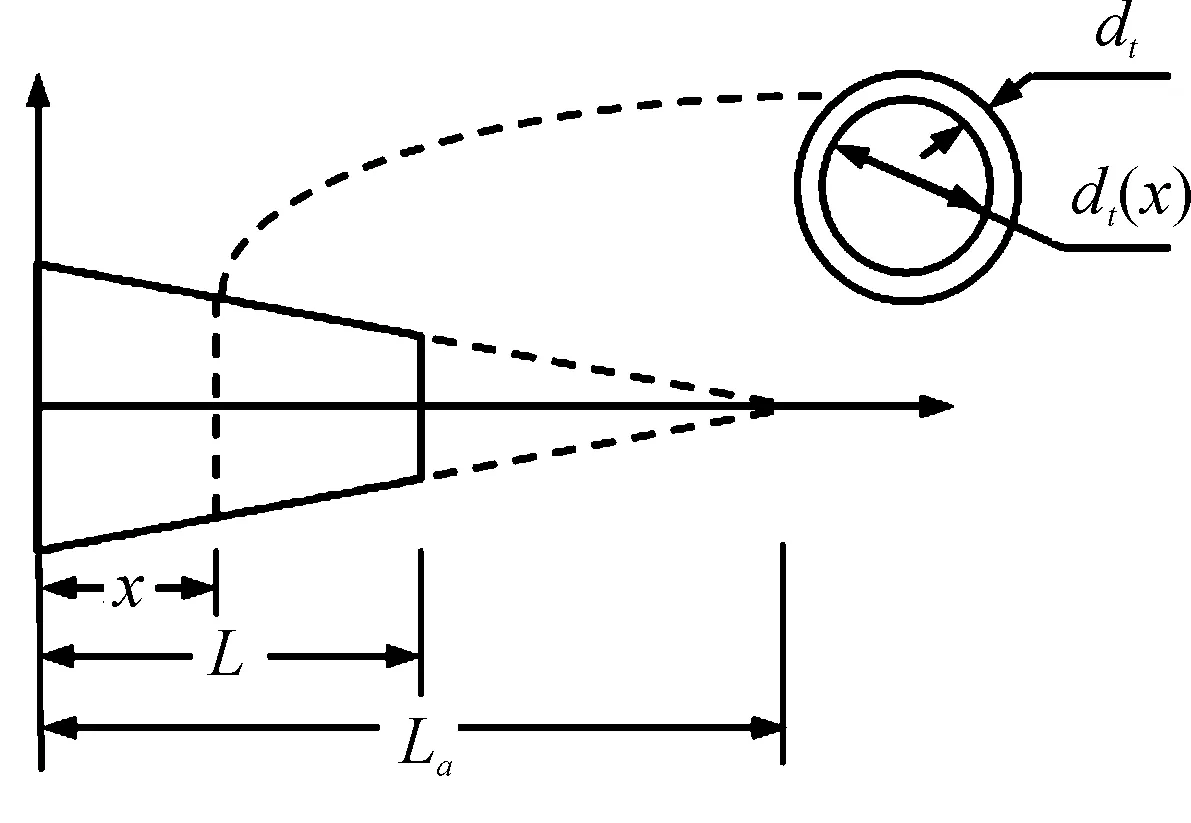
圖1 變截面管道漸變截面及截斷系數γ

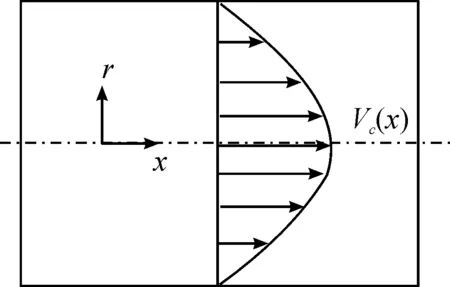
圖2 管內層流流速分布

變截面管道內徑di沿管道軸線方向x線性變化，則di(x)表達式為

(1)

管道任意截面位置x處的最大流速Vc與管道粗端處最大流速Vc0處的關系

(2)

假設管道軸線不可伸長，只考慮變截面管道的自由振動，即非保守力做功為0。利用開放系統的Hamilton原理可得到Euler-Bernoulli梁模型下兩端簡支的變截面管道的控制方程為：

(3)

2 防共振可靠性的功能函數

為了防止發生共振，應當使結構的固有頻率ω與激振力頻率S存在一定的距離。根據傳統振動設計規范的要求[8]，當1-k1<ω/S<1+k2時，認為結構設計是不安全的，易發生共振。其中k1和k2是跟材料有關的參數，對于不同的材料其參數值不同，通常在0～0.3。

令S1=(1-k1)S，S2=(1+k2)S，則S1和S2分別為激振力寬頻頻率的最小值與最大值。管道輸流工作環境復雜，ω、S1和S2的取值具有隨機性。故變截面管道的防共振可靠性的功能函數為

(4)

其中：n為固有頻率所取的最大階數，即所考慮的失效模式個數；zi(x)為第i個失效模式下的功能函數；ωi表示第i階固有頻率；x為所考慮的隨機變量向量。則可靠度的形式為：

(5)

其中：θx為隨機變量向量x的分布參數；fX為x的聯合分布概率密度函數。本文采用ALK方法對其進行求解。

3 基于ALK方法的防共振可靠性分析

3.1 Kriging插值法

Kriging插值法[9]是用處于待插值點附近的已知結構信息來模擬待插值點，故對于小樣本信息事件模擬，其具有更高的效率和精確度。Kriging模型包含已知的線性回歸模型和隨機過程模型[10]，即：

G(x)=F(x,β)+z(x)=f(x)β+z(x)

(6)

式中：G(x)表示待擬合的響應函數；f(x)表示變量x的多項式；β為多項式系數；z(x)表示一隨機過程。

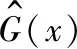
(7)

其中：y是響應值組成的n維列向量；f為單位列向量，f=[1,1,…,1]；rT(x)表示插值點x與樣本點{x(1),x(2),…,x(n)}之間的相關性：

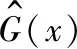
(8)

(9)

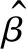
(10)

3.2 ERF學習方程

Kriging插值模型是依靠其預測點附近隨機抽樣得到的樣本點來建立的，故其模型的精度必然與所選取的樣本點有關。因此選擇加入合適的樣本點尤為重要。Bichon[11]先提出了在初始樣本點中選擇性添加新樣本點的方法來改進模型；隨后Echard[12]結合MC方法提出了的AK-MCS方法。本文采用的是YANG提出的ALK方法[7]。

由于Kriging模型給出的預測值μG(x)不是真實值，故存在其符號與真實值不同的情況。

R(x)=max[(G(x)-0),0]

(11)

R(x)表示當μG(x)<0時，真實值G(x)>0的程度。R(x)越大，G(x)越可能被錯誤預測。

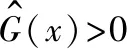
R(x)=max[(0-G(x)),0]

(12)

將兩種情況求期望并寫成統一形式，可得：

(13)

方程式(13)被稱為風險期望方程(ERF)，也被稱為學習方程。該方程表示了預測值與真實值之間符號不同的可能性大小，方程的值越大，則在該點處值的正負不同的可能性就越大。由于ERF值較大的點一般都是在極限狀態曲面附近的點以及Kriging方差很大的點，因此將這些點加入樣本點集中，可以提高Kriging模型的擬合精度。這就是主動學習的Kriging方法(ALK)。

3.3 共振可靠性分析的基本步驟

1) 取n=25，利用動剛度矩陣法求解出變截面管道的前二階固有頻率值；

2) 寫出防共振可靠性功能函數；

3) 在各隨機變量組成的不確定性域中隨機抽取Xt個初始樣本點，計算樣本點功能函數值構件初始模型。Xt=(X1,t,X2,t,…,Xn,t)(t=1,2,…,N)，取N=20；

4) 隨機產生大量候選樣本點，并計算Kriging模型的預測值μG(X)和ERF值，并將最大ERF值的點標記為X*，為使候選樣本點充滿不確定性域，取候選點數量為m=105；

5) 若ERF最大值滿足收斂條件的閾值(閾值大小設為10-3)，則進行步驟7)；

6) 若步驟5)中的收斂條件無法滿足，則將所標記的點X*加入樣本點集中，計算新加入樣本點的功能函數值，更新Kriging模型，返回步驟4)；

7) 基于最新的Kriging模型，代入Monte Carlo法中求解防共振失效概率。

4 算例

一長為L=2 m的變截面管道，其管道幾何參數及材料參數如表1所示。當變截面管道縮減系數γ=0.2，利用動剛度矩陣法求解管道的固有頻率，在計算固有頻率的過程中，采用求因變量lg(abs(h(ω)))與自變量ω的關系曲線，避免因ω采樣點分辨率過低導致的錯誤。一階固有頻率與流速的關系曲線如圖3所示。發現當Vc0=92.6 m/s時，一階固有頻率為0，即此刻輸流管道發生失穩，管道的臨界流速為92.6 m/s。

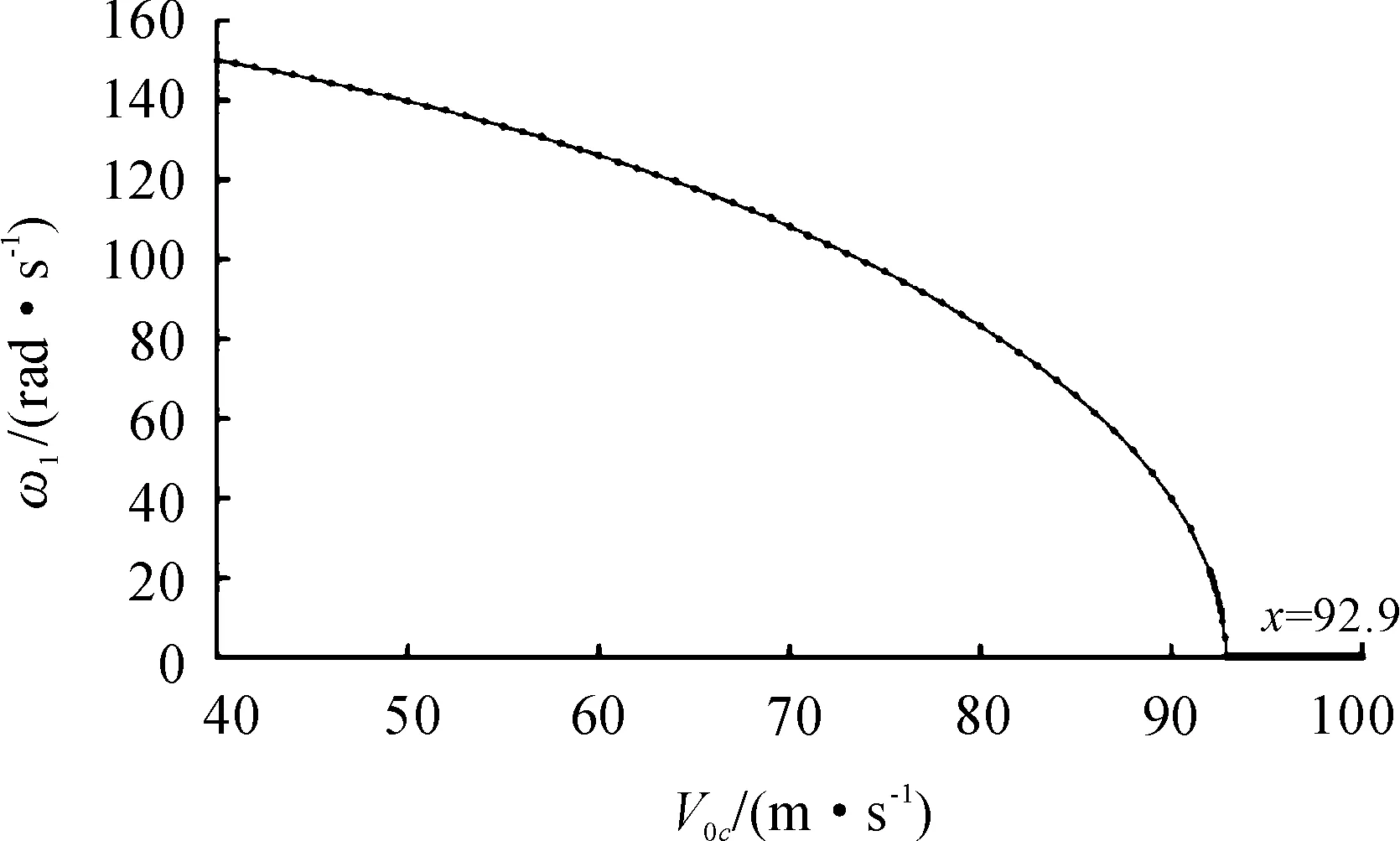
圖3 流速與一階固有頻率的關系曲線

建立功能函數，利用ALK方法計算變截面管道的共振可靠性。影響共振可靠性的隨機變量如表1所示。為了便于分析，將工況分為流速工況和截斷系數工況進行計算，截面系數與流速都服從正態分布，變異系數均為0.05。

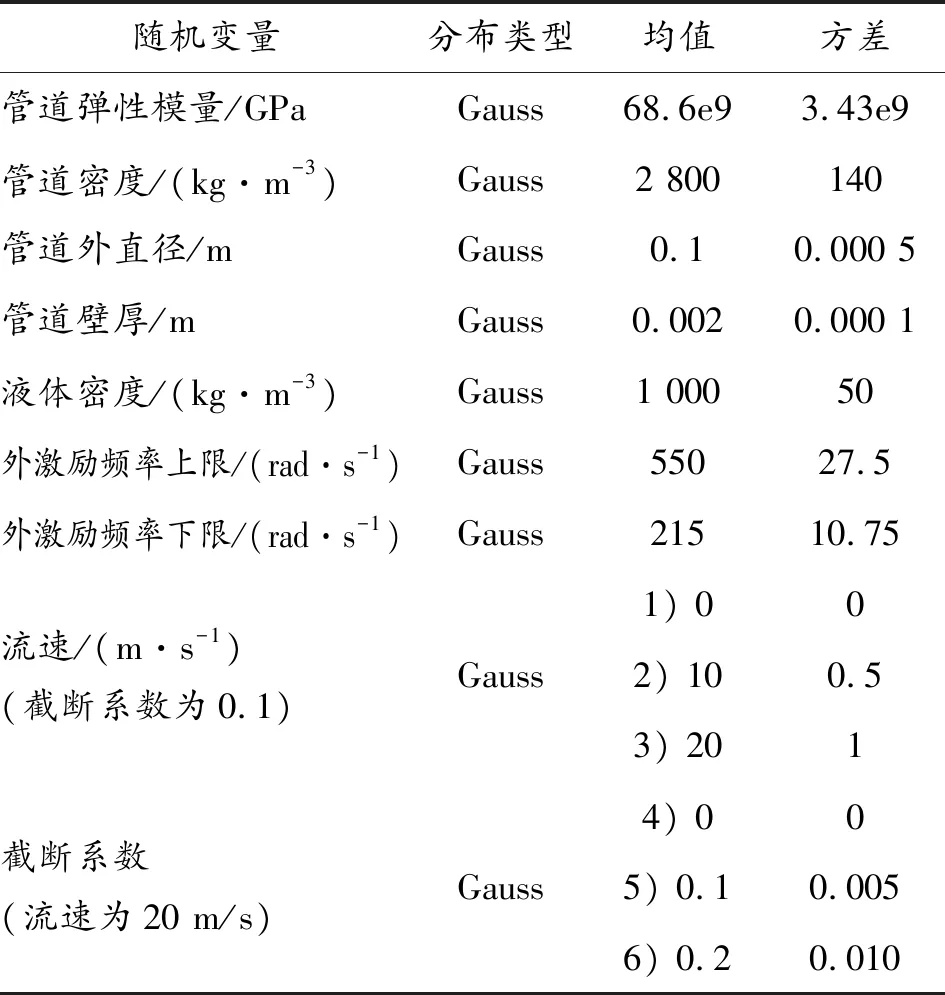
表1 隨機變量的分布類型與參數

流速工況為：①γ=0.1,Vc0=0；②γ=0.1,Vc0=10；③γ=0.1,Vc0=20；截斷系數工況為：④Vc0=0，γ=0；⑤Vc0=0,γ=0.1；⑥Vc0=0,γ=0.2。

計算結果如表2所示，從表2可看出，一階防共振失效概率隨著流速和截斷系數的增大均減小，而二階防共振失效概率則隨其增大均增大，原因在于隨著流速和截斷系數的增大，一階固有頻率減小，即不斷遠離外激勵頻率范圍，因此一階防共振失效概率逐漸減小；二階固有頻率的減小使其逐漸靠近了外激勵頻率范圍，即二階共振失效概率會逐漸增大，從而系統由一階固有頻率引起的共振轉變為二階固有頻率引起的共振。且由計算中看出，不同截斷系數對失效概率值的變化的影響更明顯。結果說明，截斷系數對于變截面輸流管道防共振失效概率具有十分重要的影響，因此，變截面輸流管道的防共振優化設計中要尤其注意截斷系數的影響。

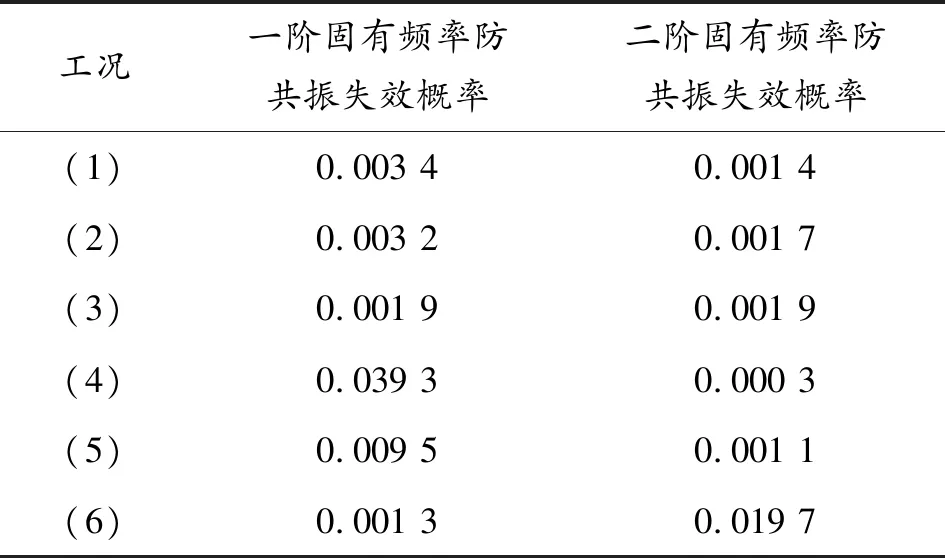
表2 不同工況下前兩階防共振失效概率

5 結論

隨著流速和截斷系數的增大，相應的固有頻率降低，使得一階固有頻率逐漸遠離外激勵頻率范圍，二階固有頻率逐漸靠近外激勵頻率范圍，從而一階防共振失效概率減小。本文所采用的ALK方法，計算高效、精確，也適用于其他隱式、非線性功能函數的復雜工程實際問題。